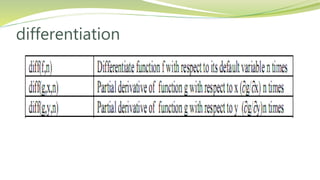
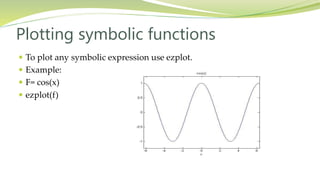
This document introduces symbolic math in MATLAB. It discusses how to create symbolic variables and expressions, perform operations like differentiation and integration symbolically, solve differential equations, compute limits, and simplify symbolic expressions. Some key capabilities covered include creating symbolic variables with sym, defining symbolic expressions, using commands like diff, int, dsolve, limit, simplify, and plotting symbolic functions with ezplot. The goal is to illustrate how to manipulate and analyze mathematical expressions symbolically in MATLAB.

1. EngMahmoud Hussein

3. Introduction
 you are used to deal with MATLAB using numerical quantities
 But till now, you couldn’t deal with MATLAB using symbols.
 Differentiation.
 Integration.
 In symbolic math, you will be able to do that.

4. Creating symbolic variables
 The sym command lets you construct symbolic variables and
expressions.
 x = sym('x')
 What is the difference between……………?
 rho = sym('(1 + sqrt(5))/2'), and
 rho = (1 + sqrt(5))/2

5. Creating Symbolic Expression
 f = sym('a*x^2 + b*x + c')
 This allows you to study the function f(x) symbolically.
 Note that in this case we don’t have symbol variables named
x, a, b, or c.
 To perform symbolic math operations (e.g.,integration, differentiation,
substitution, etc.) on f, you need to create the variables explicitly.

6. Creating Symbolic Expression
 To create the variables explicitly.
 a = sym('a')
 b = sym('b')
 c = sym('c')
 x = sym('x')
 Simply, syms a b c x
 Syms: requires less typing.
 Then enter: f = sym('a*x^2 + b*x + c')
 or simply: f = a*x^2 + b*x + c

7. Example
 syms a b
 f = a + b
 returns f = a+b
 If you then enter
 syms f
 Write: f
 MATLAB returns f = f

8. Summary

9. Operations on Symbolic Math

10. The findsym Command
 To determine what symbolic variables are present in an expression,
 Use the findsym command.
 Example:
 syms a b n t x z
 f = x^n;
 findsym(f)

11. The default symbolic variables
 The default variable for MATLAB is x.
 But if we don’t have a variable x, we can use the findsym command to
get the default variable.
 Example:
 syms s t
 g = s + t;
 findsym(g,1)

12. Solving & substitution

13. differentiation

14. Example
 Try this:
 syms x y
 f = sin(5*x)
 diff(f,2) ?
 g = exp(x)*cos(y)
 diff(g) ?

15. Solving Differential equation
 Ordinary differential equations can be solved using the dsolve
command, where D denoting differentiation.
 Example: solve the following DE.

16. Exercise
 Solve the following DE:
 Dy = - a*y
 Where y(0) = 1

17. Integration

18. Integration
 Examples

19. Limits

20. Limits
 Try this:
 f=x+2
 limit(f,x,2)

21. Limits
 The definition of the derivative is given by a
 limit provided this limit exists.
 Example:
 syms h n x
 limit( (cos(x+h) - cos(x))/h,h,0 )
 ans = -sin(x)

22. Symbolic summation
 You can compute symbolic summations,when they exist, by using the
symsum command.
 Example: the geometric series
=
 syms x k
 s = symsum(x^k,k,0,inf)

23. Laplace Transform

24. Plotting symbolic functions
 To plot any symbolic expression use ezplot.
 Example:
 F= cos(x)
 ezplot(f)

25. Symbolic simplification
 Simplify
 Collect
 Expand
 Horner
 Factor

26. Simplify
 The simplify command simplifies each element of the symbolic
expression.
 Examples:
 simplify(sin(x)^2 + cos(x)^2) returns 1
 simplify(exp(c*log(sqrt(a+b)))) returns (a+b)^(1/2*c)

27. Simplify
 Examples

28. Collect
 The statement collect(f) views f as a polynomial in its symbolic variable,
say x, and collects all the coefficients with the same power of x.

29. Expand
 The statement expand(f) distributes products over sums.
 Applies other identities involving functions of sums.

30. Horner
 The statement horner(f) transforms a symbolic polynomial f into its
nested representation.

31. Factor
 If f is a polynomial with rational coefficients factor(f) expresses f as a
product of polynomials of lower degree with rational coefficients.
 If f cannot be factored over the rational numbers, the result is f itself.