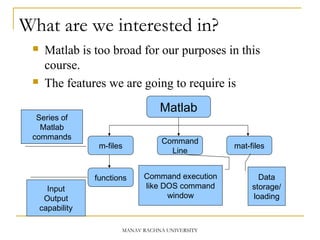
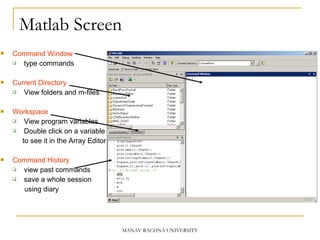
This document provides an introduction to MATLAB. It discusses what MATLAB is, the MATLAB screen interface, variables and arrays, basic arithmetic and relational operators, functions, plotting, and matrices. Key aspects covered include creating and using variables, performing calculations, controlling precision of outputs, getting help, and using basic mathematical functions in MATLAB. The document is intended to familiarize users with essential MATLAB features for use in courses.

1. Introduction to
Matlab
MANAV RACHNA UNIVERSITY

2. Outline:
 What is Matlab?
 Matlab Screen
 Variables, array, matrix, indexing
 Operators (Arithmetic, relational, logical )
 Display Facilities
 Using operators
 Using Functions
 Creating Plots
MANAV RACHNA UNIVERSITY

3. What is Matlab?
 Matlab is basically a high level language which has
many specialized toolboxes for making things easier
for us.
 Matlab stands for Matrix Laboratory.
 MATLAB provides a language and environment for
numerical computation, data analysis, visualisation
and algorithm development.
MANAV RACHNA UNIVERSITY

4.  MATLAB provides functions that operate on
 Integer, real and complex numbers
 Vectors and matrices
 Structures
4MANAV RACHNA UNIVERSITY

5. What are we interested in?
 Matlab is too broad for our purposes in this
course.
 The features we are going to require is
Matlab
Command
Line
m-files
functions
mat-files
Command execution
like DOS command
window
Series of
Matlab
commands
Input
Output
capability
Data
storage/
loading
MANAV RACHNA UNIVERSITY

6. Matlab Screen
 Command Window
 type commands
 Current Directory
 View folders and m-files
 Workspace
 View program variables
 Double click on a variable
to see it in the Array Editor
 Command History
 view past commands
 save a whole session
using diary
MANAV RACHNA UNIVERSITY

7. Variables
 No need for types. i.e.,
 All variables are created with double precision unless
specified and they are matrices.
 After these statements, the variables are 1x1 matrices
with double precision
int a;
double b;
float c;
Example:
>>x=5;
>>x1=2;
MANAV RACHNA UNIVERSITY

8. The MATLAB Interface
MANAV RACHNA UNIVERSITY
 Pressing the up arrow in the command window will
bring up the last command entered.
 This saves you time when things go wrong.
 If you want to bring up a command from some time
in the past type the first letter and press the up
arrow.
 The current working directory should be set to a
directory of your own.
8

9. MANAV RACHNA UNIVERSITY
Using MATLAB as a calculator
 Let’s start at the very beginning. For example,
suppose we want to calculate the expression, 1 + 2 ×
3. We type it at the prompt command (>>) as follows
 >> 1+2*3
 ans = 7

10. Using MATLAB as a calculator
 We will have noticed that if We do not specify an
output variable, MATLAB uses a default variable
ans, short for answer, to store the results of the
current calculation. Note that the variable ans is
created (or overwritten, if it is already existed). To
avoid this, we may assign a value to a variable or
output argument name. For example,
 >> x = 1+2*3
 x = 7
MANAV RACHNA UNIVERSITY

11. Using MATLAB as a calculator
 Will result in x being given the value 1 + 2 × 3 = 7.
This variable name can always be used to refer to the
results of the previous computations. Therefore,
computing 4x will result in
 >> 4*x
 ans = 28.0000
MANAV RACHNA UNIVERSITY

12. Creating MATLAB variables
 The syntax of variable assignment is
variable name = A value (or an expression)
 For example:
>> A=32
A=32
 To find out the value of a variable simply type the
name in
 >> A
A=32
MANAV RACHNA UNIVERSITY

13. Creating MATLAB variables
 To make another variable equal to one already entered
 >> B = A
 The new variable is not updated as you change the
original value
 Example:
 >> B=A
B= 32
 >> A=15
A=15
>> B=32
MANAV RACHNA UNIVERSITY

14. Creating MATLAB variables
 The value of two variables can be added together, and
the result displayed…
 >> A = 10
 >> A + A
 …or the result can be stored in another variable
 >> A = 10
 >> B = A + A
MANAV RACHNA UNIVERSITY

15. Creating MATLAB variables
 For Example:
 >> A=10
 A=10
 >> A+A
 ans = 20
 >> B=A+A
 B=20
MANAV RACHNA UNIVERSITY

16. Basic arithmetic operators
 Symbol Operation Example
 + Addition 2 + 3
 ∗ Multiplication 2 3∗
 − Subtraction 2 – 3
 / Division 2/3
 ^ Exponentiation 2^3
MANAV RACHNA UNIVERSITY

17. Variables
 Variables needs to be declared.
 Variable names can contain up to 63 characters.
 Variable names must start with a letter followed by
letters, digits, and underscores.
 Variable names are case sensitive.
MANAV RACHNA UNIVERSITY

18. Matlab Special Variables
 ans Default variable name for results
 pi Value of π
 eps Smallest incremental number
 inf Infinity
 NaN Not a number e.g. 0/0
 realmin The smallest usable positive real number
 realmax The largest usable positive real number
MANAV RACHNA UNIVERSITY

19. Overwriting variable
 Once a variable has been created, it can be
reassigned. In addition, if you do not wish to see the
intermediate results, you can suppress the numerical
output by putting a semicolon (;) at the end of the
line. Then the sequence of commands looks like this:
 >> t = 5;
 >> t = t+1
 t = 6
MANAV RACHNA UNIVERSITY

20. Error messages
 If we enter an expression incorrectly, MATLAB will
return an error message. For example, in the
following, we left out the multiplication sign, *, in the
following expression
 >> x = 10;
 >> 5x
 ??? 5x |
 Error: Unexpected MATLAB expression.
MANAV RACHNA UNIVERSITY

21. Making corrections
 A previously typed command can be recalled with the
up-arrow key ↑. When the command is displayed at
the command prompt, it can be modified if needed
and executed.
MANAV RACHNA UNIVERSITY

22. Controlling the hierarchy of operations
 Let’s consider the arithmetic operation, but now we
will include parentheses. For example, 1 + 2 × 3 will
become (1 + 2) × 3
 >> (1+2)*3
 ans =9
 And, from previous example
 >> 1+2*3
 ans = 7
 By adding parentheses, these two expressions give
different results: 9 and 7.
MANAV RACHNA UNIVERSITY

23.  The order in which MATLAB performs arithmetic
operations is exactly that taught in high school
algebra courses.
MANAV RACHNA UNIVERSITY

24. Hierarchy of arithmetic operations
Precedence Mathematical operations
First The contents of all parentheses are evaluated
first, starting from the innermost parentheses
and working outward.
Second All exponentials are evaluated, working from
left to right.
Third All multiplications and divisions are
evaluated, working from left to right
MANAV RACHNA UNIVERSITY

25. Controlling the appearance of floating
point number
 MATLAB by default displays only 4 decimals in the
result of the calculations, for example −163.6667, as
shown in above examples. However, MATLAB does
numerical calculations in double precision, which is 15
digits.
 >> format short
 >> x=-163.6667
MANAV RACHNA UNIVERSITY

26.  If we want to see all 15 digits, we use the command
format long
 >> format long
 >> x= -1.636666666666667e+002
 To return to the standard format, enter format short,
or simply format. There are several other formats. For
more details, see the MATLAB documentation, or
type help format.
MANAV RACHNA UNIVERSITY

27. Managing the workspace
 It is a good idea to issue a clear command at the start
of each new independent calculation.
 >> clear
 The command clear or clear all removes all variables
from the workspace. This frees up system memory. In
order to display a list of the variables currently in the
memory, type
 >> who
 While, who will give more details which include size,
space allocation, and class of the variables.
MANAV RACHNA UNIVERSITY

28. Keeping track of your work session
 It is possible to keep track of everything done during
a MATLAB session with the diary command.
 >> diary
 or give a name to a created file,
 >> diary File Name
 where File name could be any arbitrary name you
choose.
MANAV RACHNA UNIVERSITY

29. Entering multiple statements per line
 It is possible to enter multiple statements per line.
 Use commas (,) or semicolons (;) to enter more than
one statement at once.
 Commas (,) allow multiple statements per line
without suppressing output.
 Example
 >> a=7; b=cos (a), c=cosh (a)
 b = 0.6570
 c =
 548.3170
MANAV RACHNA UNIVERSITY

30. Miscellaneous commands
Here are few additional useful commands:
To clear the Command Window, type clc
To abort a MATLAB computation, type ctrl-c
To continue a line, type . . .
Getting help Information about any command is
available by typing
>> help Command
Another way to get help is to use the look for command.
MANAV RACHNA UNIVERSITY

31.  Use on-line help to request info on a specific function
>> help sqrt
 In the current version (MATLAB version 7), the doc
function opens the on-line version of the help manual.
This is very helpful for more complex commands.
>> doc plot
 Use lookfor to find functions by keywords. The
general form is
>> lookfor FunctionName
MANAV RACHNA UNIVERSITY

32. Mathematical functions
cos(x) Cosine abs(x) Absolute value
sin(x) Sine sign(x) Signum function
tan(x) Tangent max(x) Maximum value
acos(x) Arc cosine min(x) Minimum value
asin(x) Arc sine ceil(x) Round towards
+∞
atan(x) Arc tangent floor(x) Round towards −∞
exp(x) Exponential round(x) Round to nearest integer
sqrt(x) Square root rem(x) Remainder after
division
log (x) Natural logarithm angle(x) Phase angle
log10(x) Common logarithm conj(x) Complex conjugate
pi π = 3.14159 . . . Inf The infinity, ∞
i,j The imaginary unit i, √ −1
NaN Not a numberMANAV RACHNA UNIVERSITY

33. Example 1:
 the value of the expression y = e −a sin(x) + 10√y, for
a = 5, x = 2, and y = 8 is computed by
>> a = 5; x = 2; y = 8;
>> y = exp (-a)*sin(x) +10*sqrt (y)
y =
28.2904
MANAV RACHNA UNIVERSITY

34. Example 2:
 >> log (142)
ans =
4.9558
 >> log10 (142)
ans =
2.1523
 Note the difference between the natural logarithm
log(x) and the decimal logarithm (base 10) log10(x).
MANAV RACHNA UNIVERSITY

35. To calculate sin(π/4) and e10
 we enter the following commands in MATLAB,
>> sin (pi/4)
ans =
0.7071
 >> exp (10)
 ans =
2 .2026e+004
MANAV RACHNA UNIVERSITY

36. Matrix
MANAV RACHNA UNIVERSITY

37. Array, Matrix
 Entering a vector: An array of dimension 1 ×n is
called a row vector, whereas an array of
dimension m × 1 is called a column vector. The
elements of vectors in MATLAB are enclosed by
square brackets and are separated by spaces or by
commas. For example, to enter a row vector, x,
type
A = [1 2 5 1]
A =
1 2 5 1
MANAV RACHNA UNIVERSITY

38.  Column vectors are created in a similar way, however,
semicolon (;) must separate the components of a
column vector,
B = [1; 5; 3]
B =
1
5
3
 Entering a matrix: A matrix can be created in Matlab
as follows (note the commas AND semicolons):
>> matrix = [1 2 3 ; 4 5 6 ; 7 8 9]
matrix =
1 2 3
4 5 6
7 8 9
MANAV RACHNA UNIVERSITY

39. Transpose of a Matrix
On the other hand, a row vector is converted to a
column vector using the transpose operator. The
transpose operation is denoted by an apostrophe or a
single quote (’).
>> C = A’
z =
1
2
5
1
MANAV RACHNA UNIVERSITY

40.  Thus, A(1) is the first element of vector A, A(2) its
second element, and so forth.
 >>A(1)
ans= 1
>>A(2)
ans=2
 To access blocks of elements, we use MATLAB’s
colon notation (:). For example, to access the first
three elements of A, we write,
 >> A(1:3)
 ans =
 1 2 5
MANAV RACHNA UNIVERSITY

41.  Or, all elements from the third through the last
elements,
 >> A(3,end)
ans = 5 1
 where end signifies the last element in the vector. If A
is a vector, writing
 >> A( , :)
produces a column vector, whereas writing
 >> A(1:end)
produces a row vector.
MANAV RACHNA UNIVERSITY

42. Matrix Index
 The matrix indices begin from 1 (not 0 (as in C))
 The matrix indices must be positive integer
Given:
A(-2), A(0)
Error: ??? Subscript indices must either be real positive integers or logicals.
A(4,2)
Error: ??? Index exceeds matrix dimensions.
MANAV RACHNA UNIVERSITY

43. Long Array, Matrix
 Creating a vector with constant spacing by
specifying the first term, the spacing, and the last
name.
Variable_name=[m:q:n] or Variable_name = m:q:n
>> t =1:10
t =
1 2 3 4 5 6 7 8 9 10
>>k =2:-0.5:-1
k =
2 1.5 1 0.5 0 -0.5 -1
MANAV RACHNA UNIVERSITY

44.  B = [1:4; 5:8]
B =
1 2 3 4
5 6 7 8
 Creating a vector with constant spacing by specifying
the first term, and last terms, and the number of terms.
 Variable_name=linspace (xi,xe,n)
>> va=linspace(0,8,6)
Va=
0 16 3.2 4.8 6.4 8
MANAV RACHNA UNIVERSITY

45. Generating Vectors from functions
 zeros(M,N) MxN matrix of zeros
 Eye(M) MxM identity matrix
 ones(M,N) MxN matrix of ones
x = zeros(1,3)
x =
0 0 0
X= eye(3)
1 0 0
0 1 0
0 0 1
x = ones(1,3)
x =
1 1 1
MANAV RACHNA UNIVERSITY

46. Concatenation of Matrices
 x = [1 2], y = [4 5], z=[ 0 0]
A = [ x y]
1 2 4 5
B = [x ; y]
1 2
4 5
C = [x y ;z]
Error:
??? Error using ==> vertcat CAT arguments dimensions are not consistent.
MANAV RACHNA UNIVERSITY

47. Operators (arithmetic)
+ addition
- subtraction
* multiplication
/ division
^ power
’ complex conjugate transpose
MANAV RACHNA UNIVERSITY

48. Matrices Operations
Given A and B:
Addition Subtraction Product Transpose
MANAV RACHNA UNIVERSITY

49. Operators (Element by Element)
.* element-by-element multiplication
./ element-by-element division
.^ element-by-element power
MANAV RACHNA UNIVERSITY

50. The use of “.” – “Element” Operation
K= x^2
Erorr:
??? Error using ==> mpower Matrix must be square.
B=x*y
Erorr:
??? Error using ==> mtimes Inner matrix dimensions must agree.
A = [1 2 3; 5 1 4; 3 2 1]
A =
1 2 3
5 1 4
3 2 -1
y = A(3 ,:)
y=
3 4 -1
b = x .* y
b=
3 8 -3
c = x . / y
c=
0.33 0.5 -3
d = x .^2
d=
1 4 9
x = A(1,:)
x=
1 2 3
MANAV RACHNA UNIVERSITY

51. Some matrix functions in Matlab
X = ones(r,c) % Creates matrix full with ones
X = zeros(r,c) % Creates matrix full with zeros
A = diag(x) % Creates squared matrix with
vector x in diagonal
[r,c] = size(A) % Return dimensions of matrix A
+ - * / % Standard operations
.+ .- .* ./ % Wise addition, substraction,…
v = sum(A) % Vector with sum of columns
MANAV RACHNA UNIVERSITY

52. Clearing Variables
 You can use the command “clear all” to delete all the
variables present in the workspace
 You can also clear specific variables using:
>> clear Variable_Name
52MANAV RACHNA UNIVERSITY

53. Thank You…
MANAV RACHNA UNIVERSITY