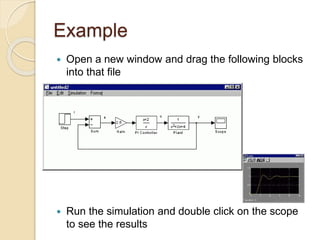
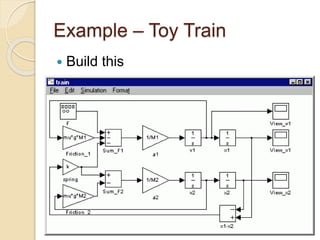
Here are the steps to solve this problem numerically in MATLAB: 1. Define the 2nd order ODE for the pendulum as two first order equations: y1' = y2 y2' = -sin(y1) 2. Create an M-file function pendulum.m that returns the right hand side: function dy = pendulum(t,y) dy = [y(2); -sin(y(1))]; end 3. Use an ODE solver like ode45 to integrate from t=0 to t=6pi with initial conditions y1(0)=pi, y2(0)=0: [t,y] = ode45

1. Introduction to
MATLAB

2. Variables
 Have not to be previously declared
 Variable names can contain up to 63 characters
 Variable names must start with a letter followed by letters, digits,
and underscores( Valid: x1 = 5, Invalid: 1x = 5)
 Variable names are case sensitive (a1 does NOT equal A1)
 EX: Using command window
 >> x = 5; % this is used as a comment
 >> y = 3;
 >> z = x + y
z = 8
 Semicolon (;) : Suppresses output
 Percentage (%) : Commenting. Only good for that line
Operators

3. MATLAB Special Variables
ans Default variable name for results
pi Value of pi number (3.14)
eps Smallest incremental number
inf Infinity
NaN Not a number e.g. 0/0
realmin The smallest usable positive real number
realmax The largest usable positive real number
i,j Imaginary unit

4. MATLAB Assignment & Operators
Assignment = a = b (assign b to a)
Addition + a + b
Subtraction - a - b
Multiplication * or.* a*b or a.*b
Division / or ./ a/b or a./b
Power ^ .^ a^b or a.^b

5. MATLAB Matrices
 MATLAB treats all variables as matrices. For our purposes a
matrix can be thought of as an array, in fact, that is how it is
stored.
 Vectors are special forms of matrices and contain only one
row OR one column.
 Scalars are matrices with only one row AND one column

6. MATLAB Matrices
 A matrix with only one row is called a row vector. A row vector can be
created in MATLAB as follows (note the commas):
» rowvec = [12 , 14 , 63]
rowvec =
12 14 63
 A matrix with only one column is called a column vector. A column
vector can be created in MATLAB as follows (note the semicolons):
» colvec = [13 ; 45; -2]
colvec =
13
45
-2

7. MATLAB Matrices
 A matrix can be created in MATLAB as follows (note the commas
AND semicolons):
» matrix = [1 , 2 , 3 ; 4 , 5 ,6 ; 7 , 8 , 9]
matrix =
1 2 3
4 5 6
7 8 9

8. Index
 MATLAB index starts with 1, NOT 0!
 Vector Index:
◦ a = [22 17 7 4 42]
 a(1) = 22
 a(3) = 7
 Matrix Index:
◦ a = [7 12 42; 5 1 23; 4 9 10];
 a(1, 3) = 42
 a(3, 2) = 9

9. Some matrix functions in MATLAB
X = ones(r,c) Creates matrix full with ones
X = zeros(r,c) Creates matrix full with zeros
A = diag(x) Creates squared matrix with vector x in diagonal
[r,c] = size(A) Return dimensions of matrix A
X = A’ Transposed matrix
X = inv(A) Inverse matrix squared matrix
X = pinv(A) Pseudo inverse
d = det(A) Determinant
[X,D] = eig(A) Eigenvalues and eigenvectors
[U,D,V] = svd(A) singular value decomposition

10. Dot Operator
 For scalar operations, nothing new is needed. Example:
a = 5; b = 3; ==> c = a*b %c = 15
 For element operations, a dot must be used before the operator.
 Note: Dot operator not the same as dot product!
 Example:
◦ a = [1 2 3 4];
◦ b = [5 6 7 8];
◦ c = a*b
◦ Result: ??? Error using ==> mtimes
inner matrix dimensions must agree
 Now, try:
◦ c = a.*b %notice the dot!
◦ Result: c=[5 12 21 32]
 Notice what it is doing: a(1)*b(1), a(2)*b(2), etc.

11. Dot Product
 Check Dimensions
◦ A*B
◦ A*B’
◦ A’*B
 Use MATLAB command
>> C=dot(A,B)
Cross Product
 By definition
 Use MATLAB command
>> C=cross(A,B)
Vector Products
Consider & generate two random 3*1 vectors, A & B
A=rand(3,1) , B=rand(3,1)
 A(2)*B(3)-A(3)*B(2)
 A(3)*B(1)-A(1)*B(3)
 A(1)*B(2)-A(2)*B(1)

12. Loops
 Loop statements do not need parenthesis. The statements
are recognized via tabs.
 3 general types of loops:
◦ If/else/elseif loops
◦ For loops
◦ While loops
 There is a 4th type, called nested loop, that can be any of the
above 3 (and any combinations of them).

13. If/else/elseif Loops
 The condition must be previously defined!

14. For Loops
 Counter variable does not have to be i; it can be any variable
 Iterations can be tightly controlled with min:stepsize:max.
 No need to pre-define the counter because you are declaring in
the for loop itself!
for i=1:10
statement
end

15. While Loops
 As long as output of condition is a logic true, it will continue
looping until the condition becomes false.
 BE CAREFUL OF INFINITE LOOPS.
while condition
statement
end

16. Nested Loops
 Can use a mix of the different types of loops.
 Very useful for performing algorithm/operations on vectors
and matrices.

17. Examples
 Write a code to print out integer numbers from 5 to 36
 Write a code to print out integers between 45 to 109 which are divisible
to 3
 Write a code to print out integers between 45 to 109 which are divisible
to 5
 Write a code :
◦ If n is divisible to 3 print “divisible to 3”
◦ elseIf n is divisible to 5 print “divisible to 5”
◦ Elseif n is divisible by 5 and 3 print “divisible by 15”

18. Section II
Feb 6st, 2016
◦ Graphing & Plots
◦ Scripts and Functions
◦ Linear & System of Equations Solving

19. Plots
 plot –plot(x,y,linespec)
◦ x and y vectors must be same length!
 subplot –subplot(m,n,p) where mxn matrix,
p = current graph
 figure –creates new window for graph
 title –creates text label at top of graph
 xlabel/ylabel–horizontal and vertical labels
for graph

20. Example
 x=0:pi/100:2*pi;
 y=sin(x);
 figure;
 plot(x,y)
◦ xlabel
◦ ylabel
◦ title
◦ figure

21. example
 x= 0:pi/100:2*pi;
 y1=sin(x);
 y2=sin(x-0.25);
 y3=sin(x-0.5);
 figure;
 plot(x,y1,x,y2,’--’,x,y3,’:’);
 legend

22. subplot
 subplot –subplot(m,n,p) where mxn matrix, p = current graph

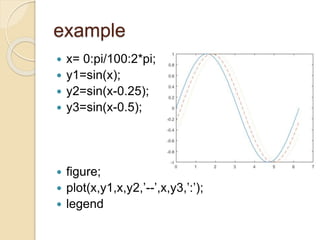
23. Axis-specific
 Helps focus on what is important on the graph.
 Change only the x or y axis limits:
◦ xlim([xminxmax]) or ylim([yminymax])
◦ min and max can be positive or negative.
 example

24. Some useful commands
 Grid on
 Hold on
 Legend
 Plot3 : example
◦ t=0:pi/50:10*pi;
◦ st=sin(t);
◦ ct=cos(t)
◦ figure;
◦ plot3(st,ct,t)

25. plotyy
 2D line plots with y-axis on both left and right side
◦ [AX,H1,H2]=plotyy(x1,y1,x2,y2)

26. Scripts & functions
 Two kind of M-files:
◦ Scripts
◦ Functions:
 With parameters and returning values
 Only visible variables defined inside the
function or parameters
 Usually one file for each function defined
 Structure:

27. Function example
 In function:
◦ function y=average(x)
◦ y=sum(x)/length(x);
◦ end
 In script:
◦ z=1:99;
◦ average(z)

28. Polynomials
 We can use an array to represent a polynomial. To do so we
use list the coefficients in decreasing order of the powers. For
example x3+4x+15 will look like [1 0 4 15]
 To find roots of this polynomial we use roots command. roots
([1 0 4 15])
 To create a polynomial from its roots poly command is used.
poly([1 2 3]) where r1=1, r2=2, r3=3
 To evaluate the new polynomial at x =5 we can use polyval
command. polyval([ 1 -6 11 -6], 5)

29. Systems of Equations
 Consider the following system of equations
◦ x+5y+15z=7
◦ x-3y+13z=3
◦ 3x-4y-15z=11
 One way to solve this system of equations is to use matrices.
First, define matrix A:
◦ A=[1 5 15; 1 -3 13; 3 -4 15];
 Second, matrix b:
◦ b=[7;3;11];
 Third, we solve the equation Ax=b for x, taking the inverse of A
and multiply it by b:
◦ x=inv(A)*b
 Note that we cannot solve equation Ax=b by dividing b by A
because vectors A and b have different dimensions!

30. Section 3
MATLAB
February 20th, 2016
◦ Symbolic Solving
◦ Systems of Equations
◦ ODE Solving
Farhad Goodarzi

31. Systems of Equations
 Consider the following system of equations
◦ x+5y+15z=7
◦ x-3y+13z=3
◦ 3x-4y-15z=11
 One way to solve this system of equations is to use matrices.
First, define matrix A:
◦ A=[1 5 15; 1 -3 13; 3 -4 15];
 Second, matrix b:
◦ b=[7;3;11];
 Third, we solve the equation Ax=b for x, taking the inverse of A
and multiply it by b:
◦ x=inv(A)*b
 Note that we cannot solve equation Ax=b by dividing b by A
because vectors A and b have different dimensions!

32. Symbolic toolbox
 Use syms command
◦ syms F3 x a b
◦ F3=sqrt(x)
◦ Int(F3,a,b)

33. Symbolic toolbox example
 Define functions
F1=6x3-4x2+bx-5, F2= Sin (y),
and
F3= Sqrt(x).
Use int() function to determine:

34. Solving ODE with dsolve, 1st
order
 First order equations
◦ y’=xy
 y=dsolve(‘Dy=y*x’,’x’)
 y=dsolve(‘Dy=y*x’,’y(1)=1’,’x’)
◦ Or
 eq1=‘Dy=y*x’;
 y=dsolve(eq1,’x’);
◦ Issues
 our expression for y(x) isn’t suited for array operations:
vectorize()
 y, as MATLAB returns it, is actually a symbol : eval()
◦ Plotting
 x = linspace(0,1,20);
 z = eval(vectorize(y));
 plot(x,z)

35. Solving ODE with dsolve, 2nd
order
 Second order equations
◦ EQ:
 eqn2 = ’D2y + 8*Dy + 2*y =cos(x)’;
 inits2 = ’y(0)=0 , Dy(0)=1’;
 y=dsolve(eqn2,inits2,’x’)
◦ Plotting
 x = linspace(0,1,20);
 z = eval(vectorize(y));
 plot(x,z)

36. Solving ODE with dsolve,
systems
 Systems of equations
◦ EQs:
 [x,y,z]=dsolve(’Dx=x+2*y-z’,’Dy=x+z’,’Dz=4*x-4*y+5*z’)
 inits=’x(0)=1,y(0)=2,z(0)=3’;
 [x,y,z]=dsolve(’Dx=x+2*y-z’,’Dy=x+z’,’Dz=4*x-4*y+5*z’,inits)
 Notice that since no independent variable was specified,
MATLAB used its default, t.
◦ Plotting
 t=linspace(0,.5,25);
 xx=eval(vectorize(x));
 yy=eval(vectorize(y));
 zz=eval(vectorize(z));
 plot(t, xx, t, yy, t, zz)

37. Solving ODE with dsolve,
systems
 solve the given differential equations symbolically.

38. ODE Solving Numerically
 Defining an ODE function in an M-file
 Solving First-Order ODEs
 Solving Systems of First-Order ODEs
 Solving higher order ODEs

39. Numerical methods are used to solve initial value
problems where it is difficult to obtain exact solutions
 MATLAB has several different built-ins
functions for numerical solution of
ODEs

40. Solvers

41. Solving first-order ODEs
 Define the function M-file
 function y_dot=EOM(y,t)
 global alpha gamma
 y_dot=alpha * y - gamma * y^2;
 end
 Make a script M-file
 global alpha gamma
 alpha=0.15;
 gamma=3.5;

 y0=1;
 [y t]=ode45(@EOM,[0 10],y0);
 plot(t,y);

42. Solving systems of ODEs
 Example
 Create function containing the equations
 Change the error tolerance using odeset
 Plotting the columns of returned vector

43. Solving a Stiff system
 Equations
 Create the function
 Ode and plotting

44. Example
 Use “ode45” to solve the following differential
equation and plot y(x) in the interval of [0,6π]. Put
your name in the plot title.

45. Solving higher-order ODE
 Project: Simple pendulum
 Equation of motion is given by:
 2nd order Nonlinear ODE
 Convert the 2nd order ODE to standard form

46. Simple Pendulum
 Initial conditions and constants
 Coding
◦ Make a function M-file for equation of motion
 function z_dot=EOM_pendulum(t,z)
 global G L
 theta=z(1);
 theta_dot=z(2);
 theta_dot2=-(G/L)*sin(theta);
 z_dot=[theta_dot;theta_dot2];
 end
◦ Make a script M-file to run the code
 global G L
 G=9.8;
 L=2;
 tspan=[0 2*pi];
 inits=[pi/3 0];
 [t, y]=ode45(@EOM_pendulum,tspan,inits);

47. Lorenz Equations
 Initials and constants, T=[0 20]
 Plot x vs. z , check if you
get same results as

48. Section 4
March 5th, 2016
◦ Simulink

49. Simulink
 >> simulink
◦ Continuous and discrete dynamics blocks, such as
Integration, Transfer functions, Transport Delay, etc.
◦ Math blocks, such as Sum, Product, Add, etc
◦ Sources, such as Ramp, Random Generator, Step, etc

50. Useful blocks
 Math and Control
 inputs and outputs

51. Example
 Open a new window and drag the following blocks
into that file
 Run the simulation and double click on the scope
to see the results

52. Example
 Open a new window and drag the following blocks
into that file
 Run the simulation and double click on the scope
to see the results

53. Example
 Open a new window and drag the following blocks
into that file
 Run the simulation and double click on the scope
to see the results

54. simple model
 Build a Simulink model that solves the differential
equation
 Initial condition
 First, sketch a simulation diagram of this mathematical
model (equation)
 Input is the forcing function 3sin(2t)
 Output is the solution of the differential equation x(t)
 
t
x 2
sin
3



55. simple model
 Build a Simulink model that solves the differential
equation
Double-click on
the Sine Wave
block to set
amplitude = 3
and freq = 2.
This produces the
desired input of
3sin(2t)

56. simple model
 It should look like this, change the initial condition
in integrator to -1

57. Example – Toy Train
 consisting of an engine and a car. Assuming that
the train only travels in one direction, we want to
apply control to the train so that it has a smooth
start-up and stop, along with a constant-speed ride
 The mass of the engine and the car will be
represented by M1 and M2, respectively. The two
are held together by a spring, which has the
stiffness coefficient of k. F represents the force
applied by the engine, and the Greek letter, mu,
represents the coefficient of rolling friction.

58. Example – Toy Train
 System

59. Example – Toy Train
 System

60. Example – Toy Train
 Build this

61. Example – Toy Train
 Before running the model, we need to assign numerical
values to each of the variables used in the model.
Create an new m-file and enter the following
commands.
 M1=1;
 M2=0.5;
 k=1;
 F=1;
 mu=0.002;
 g=9.8;
 Execute your m-file to define these values. Simulink will
recognize MATLAB variables for use in the model.

62. Pendulum Example
 Try the following blocks