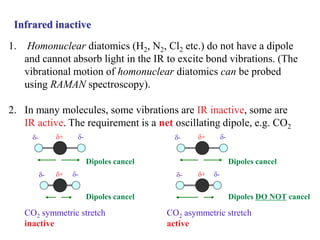
This document discusses infrared spectroscopy and its applications to analyzing molecular vibrations. It begins by explaining that atoms in molecules vibrate and infrared light can excite vibrational motions. Diatomic molecules undergo stretching vibrations, while more complex molecules also bend. The vibrational frequency depends on the force constant and reduced mass. Infrared spectroscopy can identify functional groups and provide information about molecular structure and conformation. It discusses using the amide I and amide II bands to analyze secondary structure in proteins.

1. Infrared Spectroscopy
• Atoms in a molecule do not maintain fixed
positions - they vibrate back and forth.
• The bond length is an average value.
• A diatomic molecule, e.g. H-Cl can only
undergo a STRETCHING vibration.
• More complex molecules exhibit both
STRETCHING and BENDING vibrations.
• Vibrational motion is excited within a single
electronic state by infrared light.
Vibrations of bonds involving HYDROGEN are very
significant as atoms of low mass move a lot more in
comparison to atoms of higher mass.

2. Simple Harmonic Oscillator
re
m1
m2
Hooke’s Law
The force to compress or extend
a spring is:
F(r) = – k (r - re)
Force Constant
Actual length
Equilibrium length
Strong spring - large force constant
Weak spring - small force constant
Units of force constant are: N m-1
Treat a diatomic molecule as two masses joined by a spring

3. Diatomic molecule force constants
Strong bonds have large force constants.
Molecule k/N m-1 Eb/kJ mol-1
H2 509 436
HCl 478 431
Cl2 320 242
N2 2241 945
Single bonds
triple bond
Eb = bond dissociation
energy.
Potential energy in the spring, V(r)
V(r) = k (r – re)2
1
2

4. Vibrational frequency, n
The vibrational frequency is given by:
SI Units
• Hz (or s-1) for n
• N m-1 for k
• kg (per molecule) for µ
We frequently use masses in g mol-1 (e.g. H=1, C=12, O=16 …)
 = m1 m2
m1 + m2
u kg
Where u is the unified mass
constant u = 1.66  10-27 kg
n = 1
2
k
 Hz  = m1 m2
m1 + m2
µ is the reduced mass
kg

5. Vibrational frequency - wavenumbers, cm-1
cm-1
n = 1
200c
k

The vibrational frequency
in cm-1 is given by:
The frequency is:
1. directly proportional to the force constant
2. inversely proportional to the reduced mass
Molecule k/N m-1 µ/kg n/cm-1
H2 509 8.3110-28 4159
HCl 478 1.6210-27 2890
Cl2 320 2.9110-26 557
N2 2241 1.1610-26 2331
The SI unit of wavenumber is m-1.
But cm-1 is more common.
n/m n/cm 100
n = 1/l and c = lnso n = n / c

6. Example
Suppose that the C=O group in a peptide bond can be regarded as
isolated from the rest of the molecule. Given that the force constant
of the bond in a carbonyl group is 908 N m-1, calculate
the vibrational frequency of (a) 12C=16O and (b) 13C=16O.

7. Energy levels
Classically the harmonic oscillator
can have any energy.
Quantum mechanically it only has
discrete equally spaced energy
levels given by:
v = 0, 1, 2, 3…
Ev = (v + ) hn
1
2
Selection rule
Absorption of light only occurs for ∆v = ± 1
This means that each transition has the same energy change.

8. Interaction with light
1. Light has an oscillating electric field.
2. The molecule must also possess an oscillating electric field (at
the same frequency).
3. Photon energy must equal the difference between energy levels.
1. Heteronuclear diatomics have a dipole due to the uneven
electron distribution around each atom.
2. The dipole is the product of the charge  distance apart.
3. Bond vibrations change the distance and hence the dipole
oscillates. This creates an oscillating electric field.
d+
d-
d+
d-
d+
d-
d+
d-
d+
d-
max min
Oscillating dipole

9. 1. Homonuclear diatomics (H2, N2, Cl2 etc.) do not have a dipole
and cannot absorb light in the IR to excite bond vibrations. (The
vibrational motion of homonuclear diatomics can be probed
using RAMAN spectroscopy).
2. In many molecules, some vibrations are IR inactive, some are
IR active. The requirement is a net oscillating dipole, e.g. CO2
Infrared inactive
d+
d- d-
d+
d- d-
Dipoles cancel
Dipoles cancel
CO2 symmetric stretch
inactive
d+
d- d-
d+
d- d-
Dipoles cancel
Dipoles DO NOT cancel
CO2 asymmetric stretch
active

10. Characteristic Vibrations of H2O - all IR active
symmetric stretch asymmetric stretch
n1 = 3657 cm-1 n2 = 1595 cm-1 n3 = 3756 cm-1
bend

11. Number of vibrational modes
Linear molecule with n atoms - number modes = 3n–5
e.g. CO2 n = 3 so number vib modes = 33–5 = 4
Non-linear molecule with n atoms - number modes = 3n–6
e.g. CH4 n = 5 so number vib modes = 35–6 = 9
The number of vibrational modes increases
very rapidly with n, PLUS many of these
vibrations may occur at the same frequency
and so not all of the possible bands are seen
as independent absorptions.
IR spectra are complex
Fullerene C60
174 vib modes

12. Number of vibrational modes
Linear molecule with n atoms - number modes = 3n–5
e.g. CO2 n = 3 so number vib modes = 33–5 = 4
Non-linear molecule with n atoms - number modes = 3n–6
e.g. CH4 n = 5 so number vib modes = 35–6 = 9
The number of vibrational modes increases
very rapidly with n, PLUS many of these
vibrations may occur at the same frequency
and so not all of the possible bands are seen
as independent absorptions.
IR spectra are complex
Fullerene C60
174 vib modes

13. Stretching and bending vibrations in organic molecules
Stretching vibrations can be:
(i) symmetric
(ii) asymetric
Infrared INACTIVE vibrations
• Not all vibrations result in absorption bands.
• For a vibration to cause IR absorption the dipole moment of
the molecule must change when the vibration occurs.
Bending vibrations can be:
(i) scissoring (in-plane)
(ii) rocking (in-plane)
(iii) wagging (out-of-plane)
(iv) twisting out of plane

14. • Each stretching and bending vibration of a bond is associated
with radiation whose frequency exactly matches the frequency
of the vibration of the bond.
• Different functional groups, e.g. C–C, C=C, C=O, N–H …
will have different characteristic frequencies
• Therefore, by determining the frequencies of light (IR) that are
absorbed by a particular compound we can determine what
kind of bonds it has.
IR spectra of Organic/Biological molecules
This is not as easy as it sounds

15. IR spectra of Organic molecules
Gas Phase Infrared Spectrum of Formaldehyde, H2C=O
IR spectra are often shown as % Transmittance vs Wavenumber.
So, ZERO absorption is 100% transmittance.
An absorption band appears as a trough in the spectrum. i.e. the
spectrum looks ‘upside down’.
The spectra of simple
molecules can often
be fully assigned
Wavenumber / cm-1
3n–6 = 34–6 = 6
6 vibrational modes

16. %
Transmittance
Wavenumber
IR spectra of Organic molecules
IR spectrum of 1-propanol
OH stretch
CH2
bending
CH3 stretch
Backbone
stretches
C-C stretch
1. The liquid/solid state usually produces broader lines.
2. The spectra of larger molecules are very complicated and
it is often not possible to assign all the peaks involved.
312–6 = 30
30 vibrational modes

17. Lactic Acid
OH stretches
CH3 stretches
carboxyl
stretches
Backbone
stretches
Fingerprint Region
The fingerprint region is an area of complex overlaps where it is
impossible to assign all (any?) of the bands. It can act as a unique
‘fingerprint’ for a given molecule.
Functional group Region

18. Spectral regions in the infrared
Middle IR spectrum can also be roughly divided into:
1. FUNCTIONAL GROUP REGION,  = 4000 - 1200 cm-1
2. FINGERPRINT REGION,  = 1200 - 400 cm-1
• It takes more energy to stretch a bond than bend it
• Therefore stretching bands are found in the
4000-1200 cm-1 (functional group region)
• Bends are typically observed in the fingerprint region

19. Functional group frequencies
There are extensive tables and charts available to aid in identifying
IR spectral features. It’s as much an art as a science!

20. Functional group frequencies

21. Amide I Amide II
Applications of IR to Protein structure
Amide bond of peptides has many vibrational
modes (at least 10 IR bands) these bands are
designated amide I, amide II, etc.
The frequency of Amide I depends upon the environment of
the bond and as such can be used to learn about the protein structure.
O
C
N
H
Amide I
Amide II
Protein Amide I: 1690-1600
Protein Amide II: 1575-1480

22. Amide Band Assignments
Amide A is 95% due to the the N-H stretching vibration. It is very sensitive to the
strength of the hydrogen bond.
Amide I is primarily governed by the stretching vibrations of the C=O (70-85%) and
C-N groups (10-20%).
Amide II derives mainly from in-plane N-H bending (40-60%). The rest arises from
the C-N (18-40%) and the C-C (about 10%) stretching vibrations.
Amide III, V are very complex bands dependent nature of side chains and hydrogen
bonding - only of limited use for the extraction of structural information.

23. Its frequency depends upon whether the peptide bond is in the
-helix, -sheet, or random configuration
Wavenumber /cm-1
-helix 1650
-sheet 1632, 1685
random coil 1658
Each band is well resolved so if protein contains all three
configurations 4 bands will be seen.
Amide I band