Run length encoding is a data compression technique that works by reducing the size of repeating strings of characters. It encodes repeating strings, called runs, into two bytes - the first for the run count and the second for the run value. While it achieves low compression ratios, it is easy to implement and execute quickly. Run length encoding works best on data with many repeating runs, like icons and line drawings. 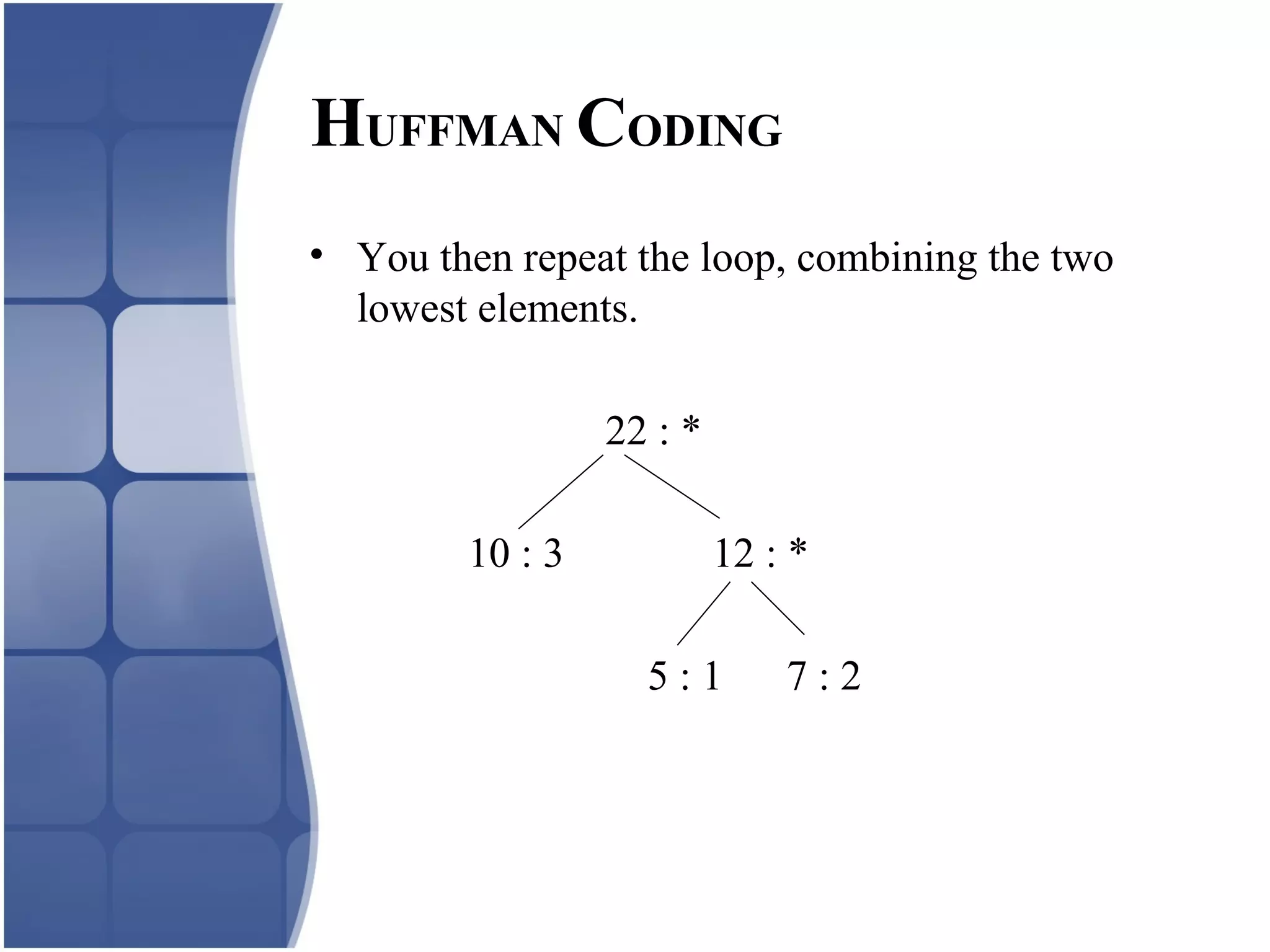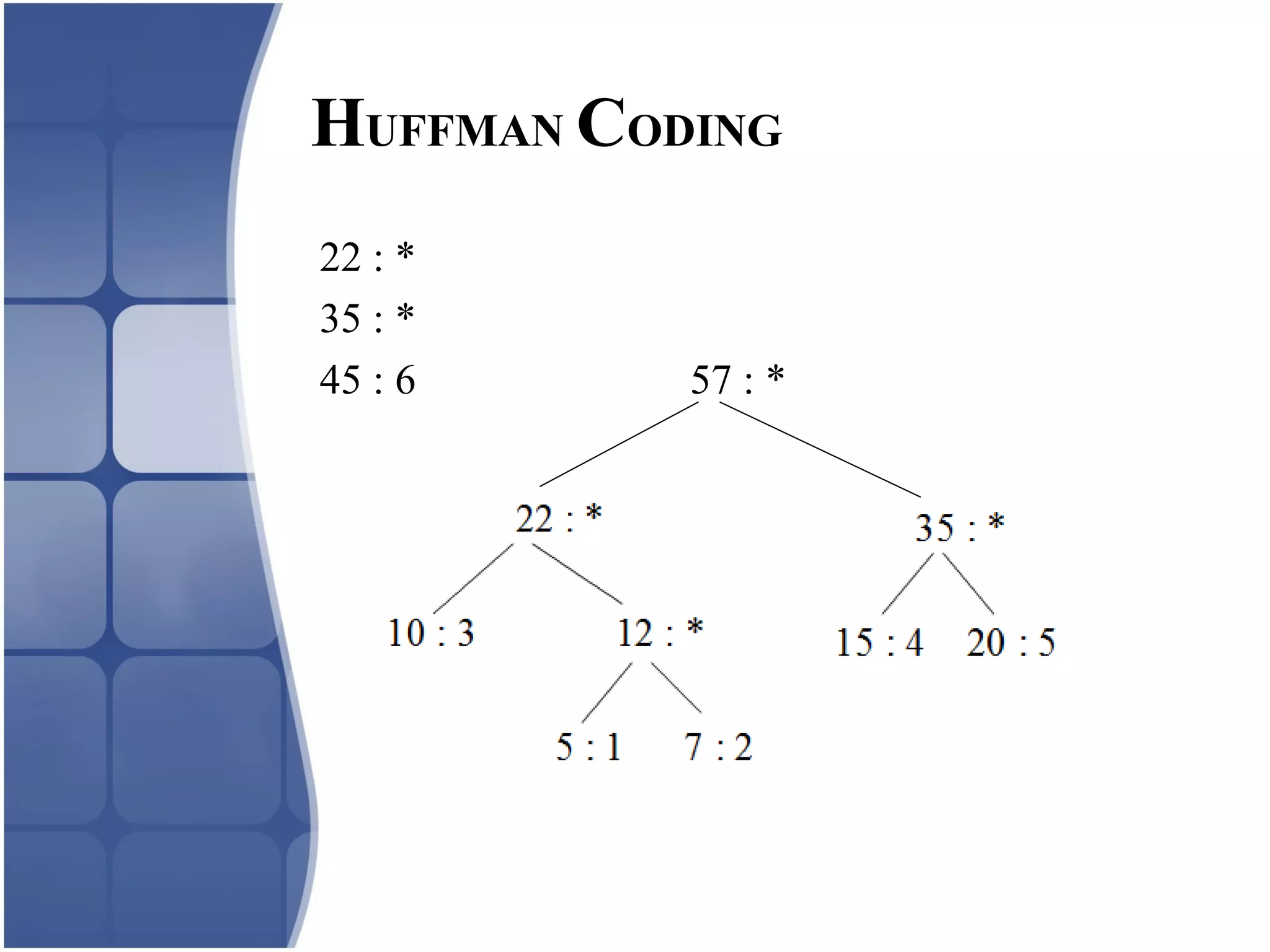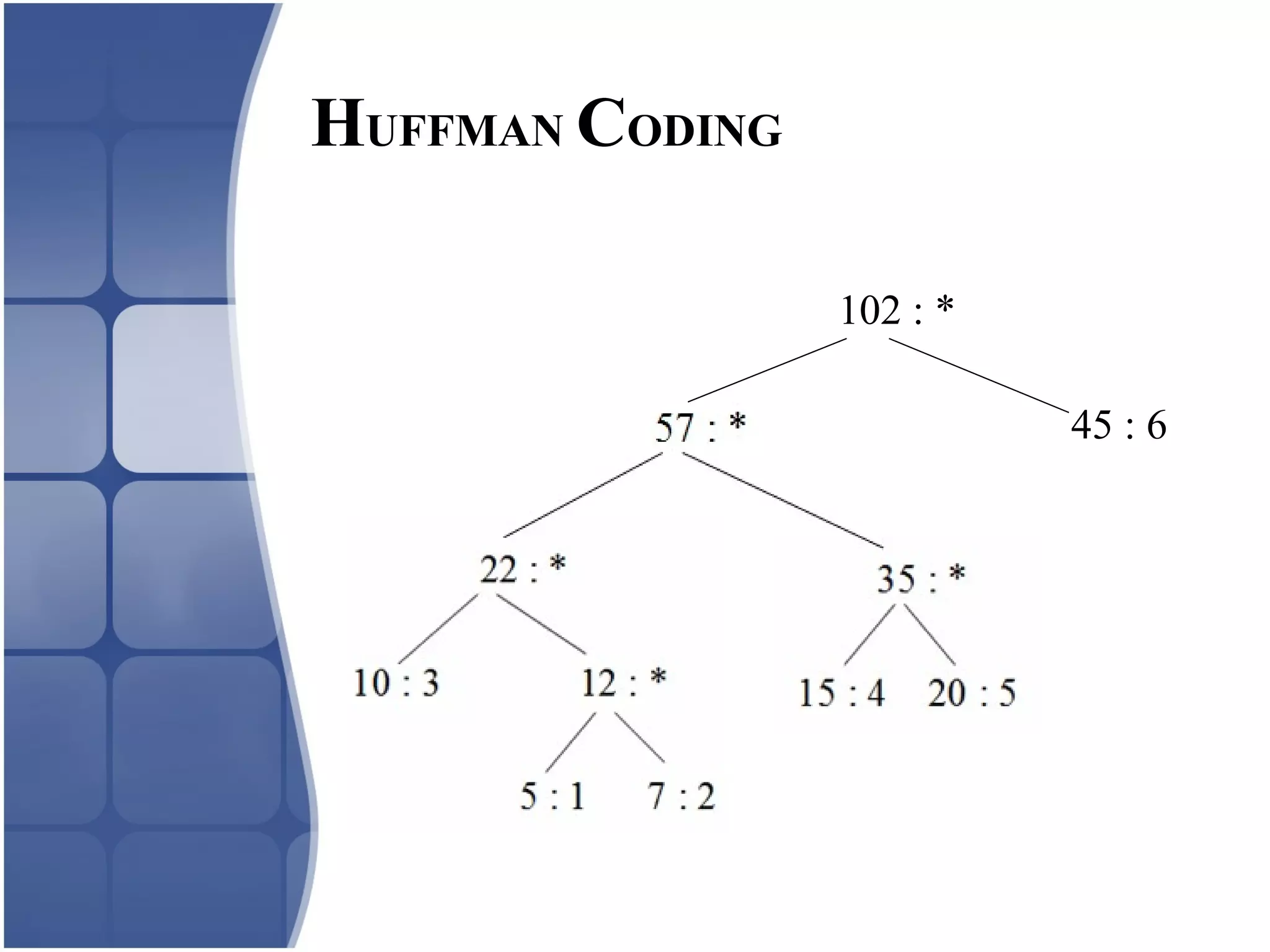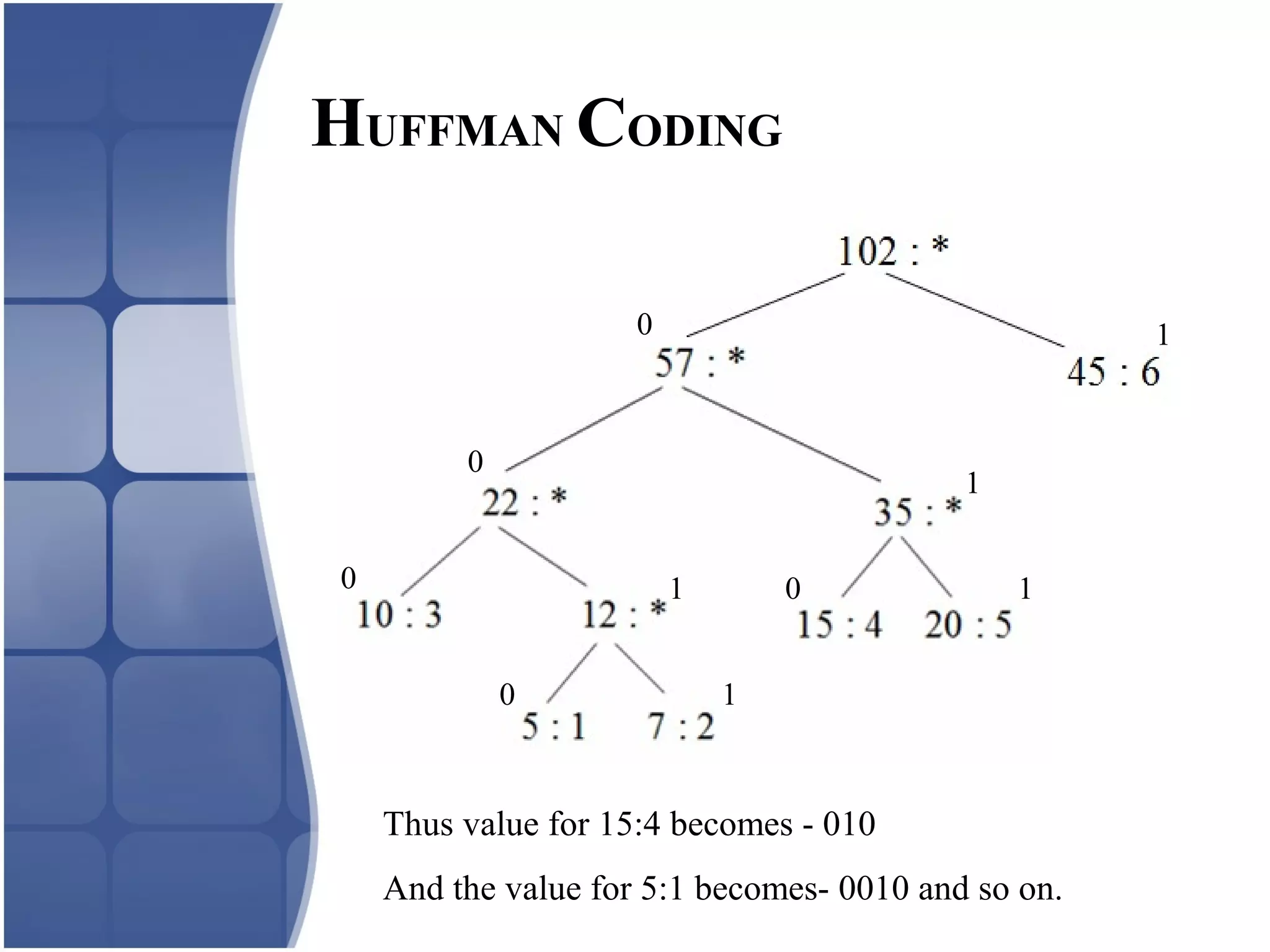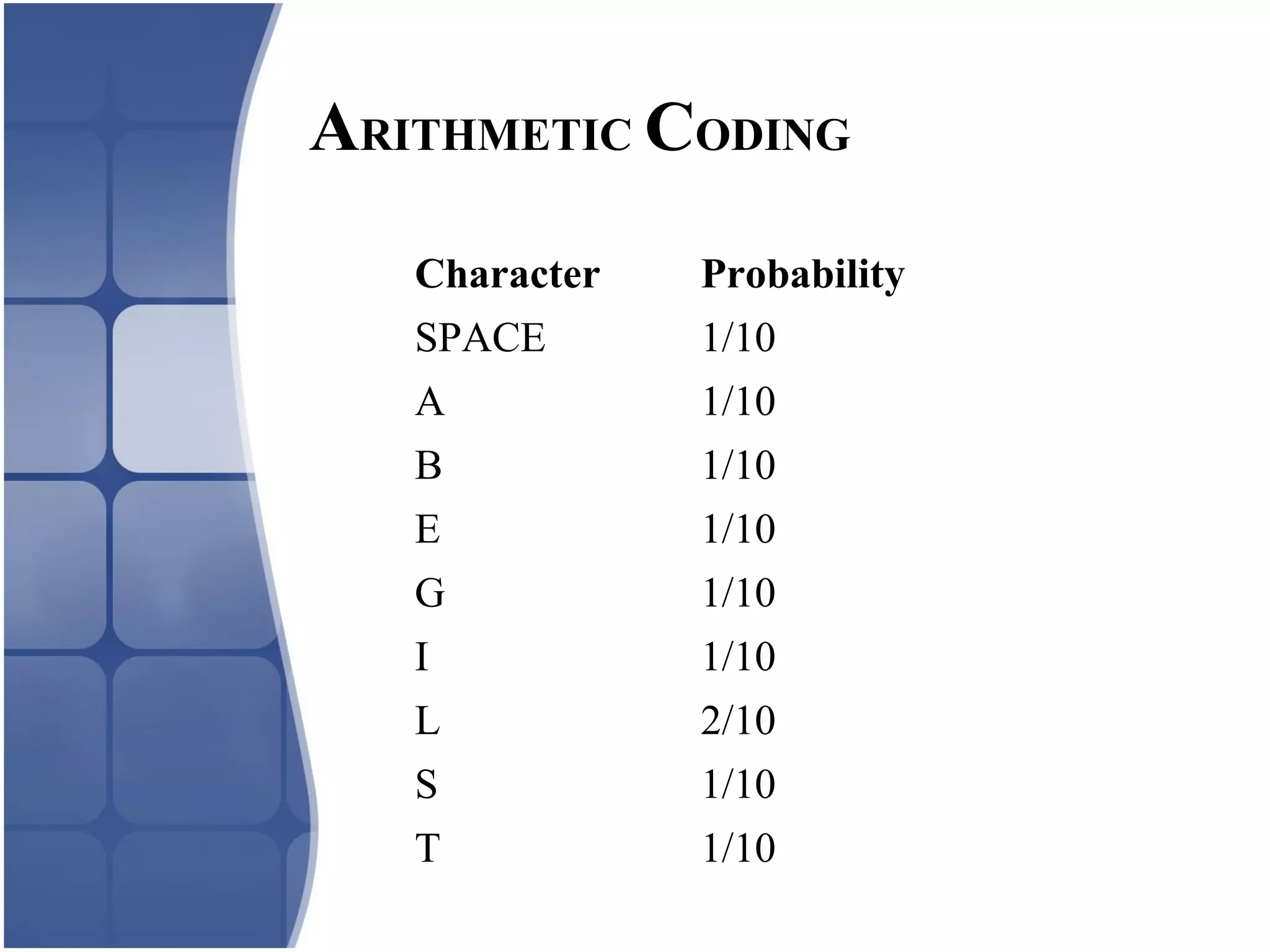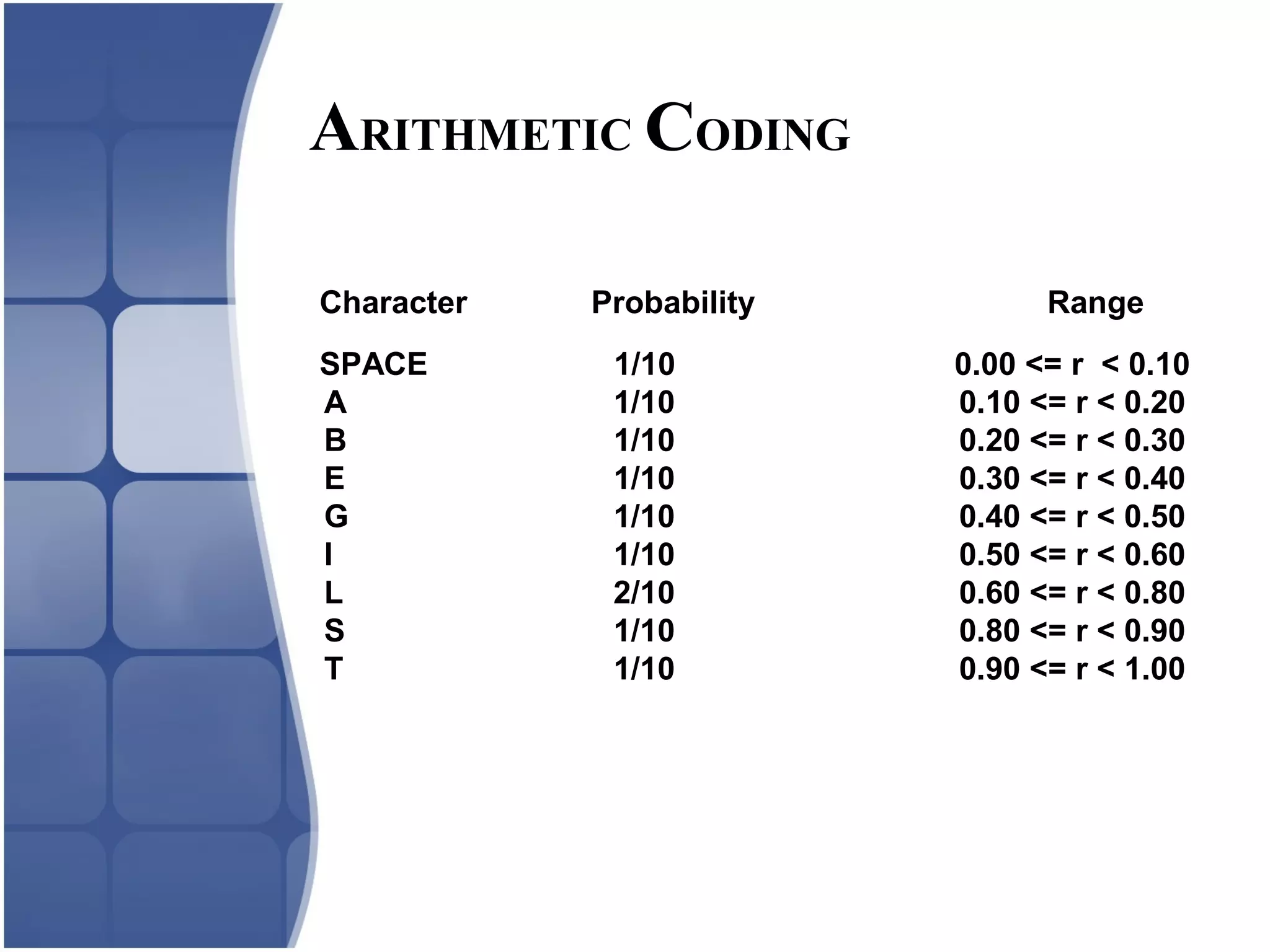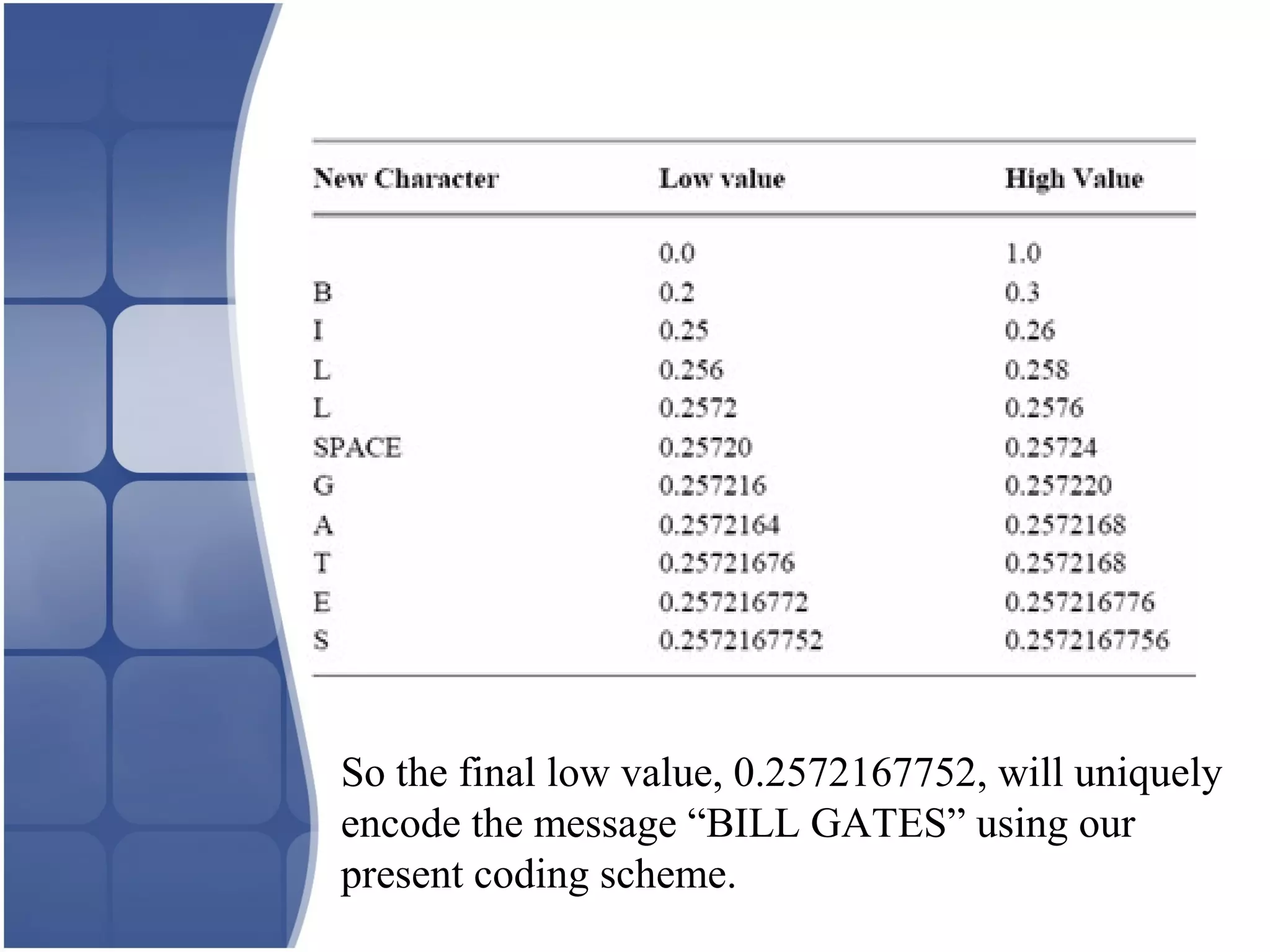Huffman coding creates an optimal variable length code by building a binary tree from the frequency of symbols in the data. It assigns shorter codes to more frequent symbols. The tree is constructed by combining the two lowest frequency nodes until only one node remains. Arithmetic coding encodes a stream of symbols into a single number between 0 and

1. INTERACTIVE
MULTIMEDIA SYSTEMS
CODING TECHNIQUES

2. RUN LENGTH CODING
• Suited for compressing any type of data
regardless of its information, but content of data
will affect the compression ratio. It achieves low
compression ratios, but easy to implement and
quick to execute. It works by reducing the size
of repeating string of characters. Repeating
strings called RUN is typically encoded into two
bytes. The first byte represents no of characters
in run & called RUN COUNT. The second byte
is value of character in run, is called run value.

3. • This is most useful on data that contains many
such runs: for example, relatively simple graphic
images such as icons, line drawings, and
animations. It is not useful with files that don't
have many runs as it could potentially double the
file size.
• RLE also refers to a little-used image format
• Consider a screen containing plain black text on a
solid white background. There will be many long
runs of white pixels in the blank space, and many
short runs of black pixels within the text. Let us take
a hypothetical single scan line, with B representing a
black pixel and W representing white:
RUN LENGTH CODING

4. • WWWWWWWWWWWWBWWWWWWWWWW
WWBBBWWWWWWWWWWWWWWW
• If we apply the run-length encoding (RLE) data
compression algorithm to the above hypothetical
scan line, we get the following:
– 12W1B12W3B15W
• Interpret this as twelve W's, one B, twelve W's, three
B's, etc.
• The run-length code represents the original 43
characters in only 13
RUN LENGTH CODING

5. HUFFMAN CODING
• Huffman coding algorithm determines the
optimal coding using minimum number of bits.
Huffman codes have the unique prefix attribute,
which means they can be correctly decoded
despite being variable length. The procedure for
building the tree is simple and elegant. The
individual symbols are laid out as a string of leaf
nodes that are going to be connected by a binary
tree. Each node has a weight, which is simply the
frequency or probability of the symbol’s
appearance.

6. • The tree is then built with the following steps
1. The two free nodes with the lowest weights are
located.
2. A parent node for these two nodes is created.
3. It is assigned a weight equal to the sum of the
two child nodes.
4. The parent node is added to the list of free
nodes, and the two child nodes are removed
from that list.
5. The previous steps are repeated until only one
free node is left. This free node is designated
the root of the tree
HUFFMAN CODING

7. • To generate a Huffman code you traverse the
tree to the value you want, outputting a 0 every
time you take a left-hand branch, and a 1 every
time you take a right-hand branch.
HUFFMAN CODING

8. • Lets say you have a set of numbers and their
frequency of use and want to create a Huffman
encoding for them:
FREQUENCY VALUE
5 1
7 2
10 3
15 4
20 5
45 6
HUFFMAN CODING

9. • Sort the list in ascending order of weights and
then just follow the steps.
• Create a parent node with a frequency that is the
sum of the two lower element's frequencies:
12:*
5:1 7:2
HUFFMAN CODING

10. • The two elements are removed from the list and
the new parent node, with frequency 12, is
inserted into the list by frequency. So now the
list, sorted by frequency, is:
10 : 3
12 : *
15 : 4
20 : 5
45 : 6
HUFFMAN CODING

11. • You then repeat the loop, combining the two
lowest elements.
22 : *
10 : 3 12 : *
5 : 1 7 : 2
HUFFMAN CODING

12. • and the list is now:
15 : 4
20 : 5
22 : *
45 : 6
• You repeat until there is only one element left in
the list.
35 : *
15 : 4 20 : 5
HUFFMAN CODING

13. 22 : *
35 : *
45 : 6 57 : *
HUFFMAN CODING

14. 102 : *
45 : 6
HUFFMAN CODING

15. HUFFMAN CODING
0
0
0
0
0
1
1
1
1
1
Thus value for 15:4 becomes - 010
And the value for 5:1 becomes- 0010 and so on.

16. ARITHMETIC CODING
• It bypasses the idea of replacing an input symbol
with a specific code. It replaces a stream of input
symbols with a single floating-point output
number. The output from an arithmetic coding
process is a single number less than 1 and
greater than or equal to 0.

17. • This single number can be uniquely decoded to
create the exact stream of symbols that went into
its construction. To construct the output
number, the symbols are assigned a set of
probabilities.
• The message “BILL GATES,” for example,
would have a probability distribution like this:
ARITHMETIC CODING

18. Character Probability
SPACE 1/10
A 1/10
B 1/10
E 1/10
G 1/10
I 1/10
L 2/10
S 1/10
T 1/10
ARITHMETIC CODING

19. • Once character probabilities are known,
individual symbols need to be assigned a range
along a “probability line,” nominally 0 to 1. The
nine-character symbol set used here would look
like the following:
ARITHMETIC CODING

20. SPACE 1/10 0.00 <= r < 0.10
A 1/10 0.10 <= r < 0.20
B 1/10 0.20 <= r < 0.30
E 1/10 0.30 <= r < 0.40
G 1/10 0.40 <= r < 0.50
I 1/10 0.50 <= r < 0.60
L 2/10 0.60 <= r < 0.80
S 1/10 0.80 <= r < 0.90
T 1/10 0.90 <= r < 1.00
Character Probability Range
ARITHMETIC CODING

21. • Each character is assigned the portion of the 0 to
1 range that corresponds to its probability of
appearance. The most significant portion of an
arithmetic-coded message belongs to the first
symbols—or B, in the message “BILL GATES.”
ARITHMETIC CODING

22. • To decode the first character properly, the final
coded message has to be a number greater than or
equal to .20 and less than .30. To encode this
number, track the range it could fall in. After the
first character is encoded, the low end for this
range is .20 and the high end is .30. During the
rest of the encoding process, each new symbol
will further restrict the possible range of the
output number. The next character to be encoded,
the letter I, owns the range .50 to .60 in the new
sub range of .2 to .3
ARITHMETIC CODING

23. • So the new encoded number will fall somewhere
in the 50th to 60th percentile of the currently
established range. Applying this logic will
further restrict our number to .25 to .26. The
algorithm to accomplish this for a message of
any length is
ARITHMETIC CODING

24. ARITHMETIC CODING

25. So the final low value, 0.2572167752, will uniquely
encode the message “BILL GATES” using our
present coding scheme.

26. Decoding The Text
• Given this encoding scheme, it is relatively easy to
see how the decoding process operates.
• Find the first symbol in the message by seeing
which symbol owns the space our encoded
message falls in.
• Since 0.2572167752 falls between .2 and .3, the
first character must be B. Then remove B from the
encoded number.
• We know the low and high ranges of B, remove
their effects by reversing the process that put them
in.

27. • Now, subtract the low value of B, giving .
0572167752. Then divide by the width of the
range of B, or .1. This gives a value of .
572167752. Then calculate where that lands,
which is in the range of the next letter, I.

28. The algorithm for decoding the incoming number is