Compression Ii
•Download as PPT, PDF•
0 likes•490 views
The document discusses various techniques for image compression including: 1) Variable length coding which reduces the first order entropy but not the second order entropy due to inter-pixel redundancy. 2) Predictive coding which codes only the difference between actual and predicted pixel values to remove inter-pixel redundancy. 3) Lossy compression techniques like transform coding and delta modulation which allow for higher compression ratios than lossless techniques by introducing some loss of information.
Report
Share
Report
Share
Recommended
Compression ii

The document discusses various techniques for image compression, including lossless and lossy methods. For lossless compression, it describes predictive coding techniques that remove inter-pixel redundancy such as delta modulation. It also covers entropy encoding schemes like Huffman coding and LZW coding. For lossy compression, it discusses the discrete cosine transform used in the JPEG standard, where higher frequency coefficients are quantized more coarsely to remove information. Zig-zag ordering is used before entropy coding the quantized DCT coefficients.
Arithmetic coding

Arithmetic coding is a lossless data compression technique that encodes data as a single real number between 0 and 1. It maps a string of symbols to a fractional number, with more probable symbols represented by larger fractional ranges. Encoding involves repeatedly dividing the interval based on symbol probabilities, and the final encoded number represents the entire string. Decoding reconstructs the string by comparing the number to symbol probability ranges. Arithmetic coding achieves compression closer to the entropy limit than Huffman coding by spreading coding inefficiencies across all symbols of the data.
Arithmetic coding

This document provides an introduction to arithmetic coding, a data compression technique. It begins with an abstract, introduction, and overview of arithmetic coding and how it differs from other entropy encoding techniques like Huffman coding. It then goes into more detail about the basic concepts, motivation, and methods behind arithmetic coding over multiple chapters. It discusses how arithmetic coding encodes data by creating a code that represents a fraction in the unit interval [0,1] and recursively partitions this interval based on the input symbols. The document provides examples to illustrate how arithmetic coding works and generates unique tags for symbol sequences.
Data Compression - Text Compression - Run Length Encoding

Run-length encoding (RLE) replaces consecutive repeated characters in data with a single character and count. For example, "aaabbc" would compress to "3a2bc". RLE works best on data with many repetitive characters like spaces. It has limitations for natural language text which contains few repetitions longer than doubles. Variants include digram encoding which compresses common letter pairs, and differencing which encodes differences between successive values like temperatures instead of absolute values.
Arithmetic coding

This document discusses arithmetic coding, a lossless data compression technique. It begins with an overview of source coding and commonly used compression algorithms like Huffman coding and run-length encoding. It then describes problems with Huffman coding like less efficiency and flexibility. Arithmetic coding is presented as an alternative with better compression ratios and adaptiveness. The document proceeds to explain the encoding and decoding process of arithmetic coding through assigning probabilities to symbols and mapping them to ranges within 0 to 1. It provides examples and figures to illustrate the technique. In summary, arithmetic coding achieves better compression than Huffman coding by producing a single codeword rather than multiple codewords.
Lec-03 Entropy Coding I: Hoffmann & Golomb Codes

This document summarizes a lecture on entropy coding and discusses Hoffman coding and Golomb coding. It begins with an overview of entropy, conditional entropy, and mutual information. It then explains Hoffman coding by describing the Hoffman coding procedure and properties like optimality. Golomb coding is also summarized, including the Golomb code construction and its advantages over unary coding. Implementation details are provided for Golomb encoding and decoding.
Arithmetic Coding

The document provides an overview of digital media basics including digitization, compression, representation, and standards. It discusses signal digitization through pulse code modulation and sampling. It also covers quantization, digitization examples, and lossless versus lossy compression. Specific compression techniques covered include transform coding, variable rate coding, predictive coding, and entropy coding like Huffman coding. The document also discusses psychoacoustic modeling and perceptual coding. It provides examples of speech, audio, image and video compression standards and techniques.
Lossless

The document discusses various lossless compression techniques including entropy coding methods like Huffman coding and arithmetic coding. It also covers dictionary-based coding like LZW, as well as spatial compression techniques like run-length coding, quadtrees for images, and lossless JPEG.
Recommended
Compression ii

The document discusses various techniques for image compression, including lossless and lossy methods. For lossless compression, it describes predictive coding techniques that remove inter-pixel redundancy such as delta modulation. It also covers entropy encoding schemes like Huffman coding and LZW coding. For lossy compression, it discusses the discrete cosine transform used in the JPEG standard, where higher frequency coefficients are quantized more coarsely to remove information. Zig-zag ordering is used before entropy coding the quantized DCT coefficients.
Arithmetic coding

Arithmetic coding is a lossless data compression technique that encodes data as a single real number between 0 and 1. It maps a string of symbols to a fractional number, with more probable symbols represented by larger fractional ranges. Encoding involves repeatedly dividing the interval based on symbol probabilities, and the final encoded number represents the entire string. Decoding reconstructs the string by comparing the number to symbol probability ranges. Arithmetic coding achieves compression closer to the entropy limit than Huffman coding by spreading coding inefficiencies across all symbols of the data.
Arithmetic coding

This document provides an introduction to arithmetic coding, a data compression technique. It begins with an abstract, introduction, and overview of arithmetic coding and how it differs from other entropy encoding techniques like Huffman coding. It then goes into more detail about the basic concepts, motivation, and methods behind arithmetic coding over multiple chapters. It discusses how arithmetic coding encodes data by creating a code that represents a fraction in the unit interval [0,1] and recursively partitions this interval based on the input symbols. The document provides examples to illustrate how arithmetic coding works and generates unique tags for symbol sequences.
Data Compression - Text Compression - Run Length Encoding

Run-length encoding (RLE) replaces consecutive repeated characters in data with a single character and count. For example, "aaabbc" would compress to "3a2bc". RLE works best on data with many repetitive characters like spaces. It has limitations for natural language text which contains few repetitions longer than doubles. Variants include digram encoding which compresses common letter pairs, and differencing which encodes differences between successive values like temperatures instead of absolute values.
Arithmetic coding

This document discusses arithmetic coding, a lossless data compression technique. It begins with an overview of source coding and commonly used compression algorithms like Huffman coding and run-length encoding. It then describes problems with Huffman coding like less efficiency and flexibility. Arithmetic coding is presented as an alternative with better compression ratios and adaptiveness. The document proceeds to explain the encoding and decoding process of arithmetic coding through assigning probabilities to symbols and mapping them to ranges within 0 to 1. It provides examples and figures to illustrate the technique. In summary, arithmetic coding achieves better compression than Huffman coding by producing a single codeword rather than multiple codewords.
Lec-03 Entropy Coding I: Hoffmann & Golomb Codes

This document summarizes a lecture on entropy coding and discusses Hoffman coding and Golomb coding. It begins with an overview of entropy, conditional entropy, and mutual information. It then explains Hoffman coding by describing the Hoffman coding procedure and properties like optimality. Golomb coding is also summarized, including the Golomb code construction and its advantages over unary coding. Implementation details are provided for Golomb encoding and decoding.
Arithmetic Coding

The document provides an overview of digital media basics including digitization, compression, representation, and standards. It discusses signal digitization through pulse code modulation and sampling. It also covers quantization, digitization examples, and lossless versus lossy compression. Specific compression techniques covered include transform coding, variable rate coding, predictive coding, and entropy coding like Huffman coding. The document also discusses psychoacoustic modeling and perceptual coding. It provides examples of speech, audio, image and video compression standards and techniques.
Lossless

The document discusses various lossless compression techniques including entropy coding methods like Huffman coding and arithmetic coding. It also covers dictionary-based coding like LZW, as well as spatial compression techniques like run-length coding, quadtrees for images, and lossless JPEG.
Text compression

Lossless Compression ,Text compression (lossless) , Run-length Encoding , Huffman Coding , Shannon-FANO Coding.
Huffman Coding

The document provides an overview of Huffman coding, a lossless data compression algorithm. It begins with a simple example to illustrate the basic idea of assigning shorter codes to more frequent symbols. It then defines key terms like entropy and describes the Huffman coding algorithm, which constructs an optimal prefix code from the frequency of symbols in the data. The document discusses how Huffman coding can be applied to image compression by first predicting pixel values and then encoding the residuals. It notes some disadvantages of Huffman coding and describes variations like adaptive Huffman coding.
Interpixel redundancy

The document discusses various techniques for image compression including:
- Run-length coding which encodes repeating pixel values and their lengths.
- Difference coding which encodes the differences between pixel values.
- Block truncation coding which divides images into blocks and assigns codewords.
- Predictive coding which predicts pixel values from neighbors and encodes differences.
Reversible compression allows exact reconstruction while lossy compression sacrifices some information for higher compression but images remain visually similar. Combining techniques can achieve even higher compression ratios.
Huffman and Arithmetic coding - Performance analysis

Huffman coding and arithmetic coding are analyzed for complexity.
Huffman coding assigns variable length codes to symbols based on probability and has O(N2) complexity. Arithmetic coding encodes the entire message as a fraction between 0 and 1 by dividing intervals based on symbol probability and has better O(N log n) complexity. Arithmetic coding compresses data more efficiently with fewer bits per symbol and has lower complexity than Huffman coding asymptotically.
Source coding theorem

The document discusses the source coding theorem, which establishes fundamental limits on lossy communication over error-free channels where the goal is information compression. It addresses how to determine the smallest rate needed to convey information about a source to a user while constraining the average error introduced by compression to a maximum level D. This problem is studied by rate distortion theory, which models the encoding-decoding process as a deterministic channel and defines a distortion measure for the penalty between source and decoded outputs. The rate distortion function gives the minimum mutual information needed to satisfy a given distortion level D.
Lec7 8 9_10 coding techniques

Run length encoding is a data compression technique that works by reducing the size of repeating strings of characters. It encodes repeating strings, called runs, into two bytes - the first for the run count and the second for the run value. While it achieves low compression ratios, it is easy to implement and execute quickly. Run length encoding works best on data with many repeating runs, like icons and line drawings.
Huffman coding creates an optimal variable length code by building a binary tree from the frequency of symbols in the data. It assigns shorter codes to more frequent symbols. The tree is constructed by combining the two lowest frequency nodes until only one node remains. Arithmetic coding encodes a stream of symbols into a single number between 0 and
Dictionary Based Compression

This document discusses various data compression techniques. It begins with an introduction to compression and its goals of reducing storage space and transmission time. Then it discusses lossless techniques like Huffman coding, Lempel-Ziv coding, run-length encoding and pattern substitution. The document also briefly covers lossy compression and entropy encoding algorithms like Shannon-Fano coding and arithmetic coding. Key compression methods and their applications are summarized throughout.
Adaptive Huffman Coding

Adaptive Huffman coding is an improvement over standard Huffman coding that allows the Huffman tree to be adapted as additional symbols are encoded. It determines codeword mappings using a running estimate of symbol probabilities. This allows it to better exploit locality in the data. The algorithm works in two phases: first, it transforms the existing Huffman tree to maintain optimality when a symbol's weight is incremented; second, it increments the weight. This process is repeated as each new symbol is encoded.
Data Communication & Computer network: Shanon fano coding

These slides cover the fundamentals of data communication & networking. it covers Shanon fano coding which are used in communication of data over transmission medium. it is useful for engineering students & also for the candidates who want to master data communication & computer networking.
Shannon Fano

The document discusses Shannon-Fano encoding, which is an early method for data compression that constructs efficient binary codes for information sources without memory. It works by assigning shorter codes to more frequent messages and longer codes to less frequent messages. The encoding process involves recursively splitting the set of messages in half based on probability until each message has its own unique code. While Shannon-Fano codes are reasonably efficient, they are not always optimal and the codes generated can depend on how the initial splitting of messages is done.
Huffman Algorithm and its Application by Ekansh Agarwal

This presentation contains the explanation on the topic Huffman algorithm backed by a sample problem for explaination
Source coding 

The document discusses information theory and source coding. It defines information and entropy, explaining that the amount of information contained in a message depends on its probability. The entropy of a data source measures the average information content. Huffman coding is presented as a method to assign variable-length codes to symbols to minimize the average code length. Error detection and correction codes are also summarized, including parity checking, cyclic redundancy checks (CRC), linear block codes, and convolutional codes.
Multimedia lossless compression algorithms

This document discusses various lossless compression algorithms including run-length coding, Shannon-Fano algorithm, Huffman coding, extended Huffman coding, dictionary-based coding like LZW, and arithmetic coding. It provides details on the basic principles of run-length coding, an example of extended Huffman coding for a source with symbols A, B, and C, and outlines the structure of the document.
Error Control Coding -Introduction

This chapter provides an introductory lecture note on the Error Control Coding techniques. Before one goes into the details of different types of Coding schemes, this note will acquaint the readers with all the terms related and associated to Error Control Coding. It is highly recommended that one goes through this article before delving deep into the coding schemes.
Module 4 Arithmetic Coding

This document discusses arithmetic coding, a technique for data compression. It begins by explaining how real numbers can be represented in binary and how this relates to encoding strings based on their probabilities. The document then provides examples of how to generate codes for strings and explains the coding and decoding algorithms. It discusses issues like scaling, integer arithmetic coding, adaptation of probabilities, and handling zero frequency and end of file problems. In the end, it compares arithmetic coding to Huffman coding, noting their similarities and differences in terms of compression performance, context handling, and adaptation.
Hamming codes

Richard Hamming developed Hamming codes in the late 1940s to enable error correction in computing. Hamming codes are perfect 1-error correcting codes that use parity checks to detect and correct single bit errors in binary data. The codes work by encoding k message bits into an n-bit codeword with additional parity check bits such that the minimum distance between any two codewords is 3, allowing correction of single bit errors. Hamming codes see widespread use and can be generalized to non-binary alphabets. Extended Hamming codes provide both single-error correction and double-error detection.
Source coding

This document summarizes several source coding techniques: Arithmetic coding encodes a message into a single floating point number between 0 and 1. Lempel-Ziv coding builds a dictionary to encode repeated patterns. Run length encoding replaces repeated characters with a code indicating the character and number of repeats. Rate distortion theory calculates the minimum bit rate needed for a given source and distortion. The entropy rate measures how entropy grows with the length of a stochastic process. JPEG uses lossy compression including discrete cosine transform and quantization to discard high frequency data imperceptible to humans.
Multimedia Communication Lec02: Info Theory and Entropy

Introduction of info theory basis for image/video coding, especially, entropy, rate-distortion theory,
entropy coding, huffman coding, arithmetic coding
ECE 4490 Multimedia Communication Lec01

This document outlines the syllabus for a Multimedia Communication class taught by Zhu Li in spring 2016. The class will cover topics related to video coding standards, video compression techniques, and video networking. Students will complete homework assignments, two quizzes, and a project. The goal of the class is for students to understand multimedia compression theory and algorithms, and be able to apply their knowledge to solve real-world problems in media communication.
Channel coding 

Channel coding is used to reduce error rates when digital communication encounters unacceptable errors over noisy channels. It works by mapping fixed-length message blocks to longer codewords with added check bits for error detection and correction. There are two main schemes for dealing with errors - Automatic Repeat Request retransmits codewords until error-free, while Forward Error Correction can detect and fix bit errors directly. The minimum distance of a code determines its ability to detect and correct errors using Hamming distance calculations during decoding. Bounds like the Hamming Bound provide the maximum number of codewords a code can contain to guarantee certain error correction capabilities.
2.3 unit-ii-text-compression-a-outline-compression-techniques-run-length-codi...

This document discusses various techniques for lossless data compression, including run-length coding, Huffman coding, adaptive Huffman coding, arithmetic coding, and Shannon-Fano coding. It provides details on how each technique works, such as assigning shorter codes to more frequent symbols in Huffman coding and dynamically updating codes based on the data stream in adaptive Huffman coding. The document also discusses the importance of compression techniques for reducing the number of bits needed to store or transmit data.
Turbo Code 

This document discusses turbo and turbo-like codes. It begins with an introduction to turbo codes, describing them as a class of high-performance error correction codes that were the first practical codes to closely approach channel capacity. It then covers channel coding, Shannon's theory, existing coding schemes like block codes and convolutional codes, and the need for better codes. The document spends significant time explaining turbo codes in detail, including their structure using parallel concatenated convolutional codes, interleaving, and iterative decoding. It also discusses related coding schemes like turbo product codes and low-density parity check codes. Finally, it reviews the performance, practical issues, applications in standards, and future trends of turbo and turbo-like codes.
More Related Content
What's hot
Text compression

Lossless Compression ,Text compression (lossless) , Run-length Encoding , Huffman Coding , Shannon-FANO Coding.
Huffman Coding

The document provides an overview of Huffman coding, a lossless data compression algorithm. It begins with a simple example to illustrate the basic idea of assigning shorter codes to more frequent symbols. It then defines key terms like entropy and describes the Huffman coding algorithm, which constructs an optimal prefix code from the frequency of symbols in the data. The document discusses how Huffman coding can be applied to image compression by first predicting pixel values and then encoding the residuals. It notes some disadvantages of Huffman coding and describes variations like adaptive Huffman coding.
Interpixel redundancy

The document discusses various techniques for image compression including:
- Run-length coding which encodes repeating pixel values and their lengths.
- Difference coding which encodes the differences between pixel values.
- Block truncation coding which divides images into blocks and assigns codewords.
- Predictive coding which predicts pixel values from neighbors and encodes differences.
Reversible compression allows exact reconstruction while lossy compression sacrifices some information for higher compression but images remain visually similar. Combining techniques can achieve even higher compression ratios.
Huffman and Arithmetic coding - Performance analysis

Huffman coding and arithmetic coding are analyzed for complexity.
Huffman coding assigns variable length codes to symbols based on probability and has O(N2) complexity. Arithmetic coding encodes the entire message as a fraction between 0 and 1 by dividing intervals based on symbol probability and has better O(N log n) complexity. Arithmetic coding compresses data more efficiently with fewer bits per symbol and has lower complexity than Huffman coding asymptotically.
Source coding theorem

The document discusses the source coding theorem, which establishes fundamental limits on lossy communication over error-free channels where the goal is information compression. It addresses how to determine the smallest rate needed to convey information about a source to a user while constraining the average error introduced by compression to a maximum level D. This problem is studied by rate distortion theory, which models the encoding-decoding process as a deterministic channel and defines a distortion measure for the penalty between source and decoded outputs. The rate distortion function gives the minimum mutual information needed to satisfy a given distortion level D.
Lec7 8 9_10 coding techniques

Run length encoding is a data compression technique that works by reducing the size of repeating strings of characters. It encodes repeating strings, called runs, into two bytes - the first for the run count and the second for the run value. While it achieves low compression ratios, it is easy to implement and execute quickly. Run length encoding works best on data with many repeating runs, like icons and line drawings.
Huffman coding creates an optimal variable length code by building a binary tree from the frequency of symbols in the data. It assigns shorter codes to more frequent symbols. The tree is constructed by combining the two lowest frequency nodes until only one node remains. Arithmetic coding encodes a stream of symbols into a single number between 0 and
Dictionary Based Compression

This document discusses various data compression techniques. It begins with an introduction to compression and its goals of reducing storage space and transmission time. Then it discusses lossless techniques like Huffman coding, Lempel-Ziv coding, run-length encoding and pattern substitution. The document also briefly covers lossy compression and entropy encoding algorithms like Shannon-Fano coding and arithmetic coding. Key compression methods and their applications are summarized throughout.
Adaptive Huffman Coding

Adaptive Huffman coding is an improvement over standard Huffman coding that allows the Huffman tree to be adapted as additional symbols are encoded. It determines codeword mappings using a running estimate of symbol probabilities. This allows it to better exploit locality in the data. The algorithm works in two phases: first, it transforms the existing Huffman tree to maintain optimality when a symbol's weight is incremented; second, it increments the weight. This process is repeated as each new symbol is encoded.
Data Communication & Computer network: Shanon fano coding

These slides cover the fundamentals of data communication & networking. it covers Shanon fano coding which are used in communication of data over transmission medium. it is useful for engineering students & also for the candidates who want to master data communication & computer networking.
Shannon Fano

The document discusses Shannon-Fano encoding, which is an early method for data compression that constructs efficient binary codes for information sources without memory. It works by assigning shorter codes to more frequent messages and longer codes to less frequent messages. The encoding process involves recursively splitting the set of messages in half based on probability until each message has its own unique code. While Shannon-Fano codes are reasonably efficient, they are not always optimal and the codes generated can depend on how the initial splitting of messages is done.
Huffman Algorithm and its Application by Ekansh Agarwal

This presentation contains the explanation on the topic Huffman algorithm backed by a sample problem for explaination
Source coding 

The document discusses information theory and source coding. It defines information and entropy, explaining that the amount of information contained in a message depends on its probability. The entropy of a data source measures the average information content. Huffman coding is presented as a method to assign variable-length codes to symbols to minimize the average code length. Error detection and correction codes are also summarized, including parity checking, cyclic redundancy checks (CRC), linear block codes, and convolutional codes.
Multimedia lossless compression algorithms

This document discusses various lossless compression algorithms including run-length coding, Shannon-Fano algorithm, Huffman coding, extended Huffman coding, dictionary-based coding like LZW, and arithmetic coding. It provides details on the basic principles of run-length coding, an example of extended Huffman coding for a source with symbols A, B, and C, and outlines the structure of the document.
Error Control Coding -Introduction

This chapter provides an introductory lecture note on the Error Control Coding techniques. Before one goes into the details of different types of Coding schemes, this note will acquaint the readers with all the terms related and associated to Error Control Coding. It is highly recommended that one goes through this article before delving deep into the coding schemes.
Module 4 Arithmetic Coding

This document discusses arithmetic coding, a technique for data compression. It begins by explaining how real numbers can be represented in binary and how this relates to encoding strings based on their probabilities. The document then provides examples of how to generate codes for strings and explains the coding and decoding algorithms. It discusses issues like scaling, integer arithmetic coding, adaptation of probabilities, and handling zero frequency and end of file problems. In the end, it compares arithmetic coding to Huffman coding, noting their similarities and differences in terms of compression performance, context handling, and adaptation.
Hamming codes

Richard Hamming developed Hamming codes in the late 1940s to enable error correction in computing. Hamming codes are perfect 1-error correcting codes that use parity checks to detect and correct single bit errors in binary data. The codes work by encoding k message bits into an n-bit codeword with additional parity check bits such that the minimum distance between any two codewords is 3, allowing correction of single bit errors. Hamming codes see widespread use and can be generalized to non-binary alphabets. Extended Hamming codes provide both single-error correction and double-error detection.
Source coding

This document summarizes several source coding techniques: Arithmetic coding encodes a message into a single floating point number between 0 and 1. Lempel-Ziv coding builds a dictionary to encode repeated patterns. Run length encoding replaces repeated characters with a code indicating the character and number of repeats. Rate distortion theory calculates the minimum bit rate needed for a given source and distortion. The entropy rate measures how entropy grows with the length of a stochastic process. JPEG uses lossy compression including discrete cosine transform and quantization to discard high frequency data imperceptible to humans.
Multimedia Communication Lec02: Info Theory and Entropy

Introduction of info theory basis for image/video coding, especially, entropy, rate-distortion theory,
entropy coding, huffman coding, arithmetic coding
ECE 4490 Multimedia Communication Lec01

This document outlines the syllabus for a Multimedia Communication class taught by Zhu Li in spring 2016. The class will cover topics related to video coding standards, video compression techniques, and video networking. Students will complete homework assignments, two quizzes, and a project. The goal of the class is for students to understand multimedia compression theory and algorithms, and be able to apply their knowledge to solve real-world problems in media communication.
Channel coding 

Channel coding is used to reduce error rates when digital communication encounters unacceptable errors over noisy channels. It works by mapping fixed-length message blocks to longer codewords with added check bits for error detection and correction. There are two main schemes for dealing with errors - Automatic Repeat Request retransmits codewords until error-free, while Forward Error Correction can detect and fix bit errors directly. The minimum distance of a code determines its ability to detect and correct errors using Hamming distance calculations during decoding. Bounds like the Hamming Bound provide the maximum number of codewords a code can contain to guarantee certain error correction capabilities.
What's hot (20)
Huffman and Arithmetic coding - Performance analysis

Huffman and Arithmetic coding - Performance analysis
Data Communication & Computer network: Shanon fano coding

Data Communication & Computer network: Shanon fano coding
Huffman Algorithm and its Application by Ekansh Agarwal

Huffman Algorithm and its Application by Ekansh Agarwal
Multimedia Communication Lec02: Info Theory and Entropy

Multimedia Communication Lec02: Info Theory and Entropy
Similar to Compression Ii
2.3 unit-ii-text-compression-a-outline-compression-techniques-run-length-codi...

This document discusses various techniques for lossless data compression, including run-length coding, Huffman coding, adaptive Huffman coding, arithmetic coding, and Shannon-Fano coding. It provides details on how each technique works, such as assigning shorter codes to more frequent symbols in Huffman coding and dynamically updating codes based on the data stream in adaptive Huffman coding. The document also discusses the importance of compression techniques for reducing the number of bits needed to store or transmit data.
Turbo Code 

This document discusses turbo and turbo-like codes. It begins with an introduction to turbo codes, describing them as a class of high-performance error correction codes that were the first practical codes to closely approach channel capacity. It then covers channel coding, Shannon's theory, existing coding schemes like block codes and convolutional codes, and the need for better codes. The document spends significant time explaining turbo codes in detail, including their structure using parallel concatenated convolutional codes, interleaving, and iterative decoding. It also discusses related coding schemes like turbo product codes and low-density parity check codes. Finally, it reviews the performance, practical issues, applications in standards, and future trends of turbo and turbo-like codes.
Image compression

This document summarizes image compression techniques. It discusses:
1) The goal of image compression is to reduce the amount of data required to represent a digital image while preserving as much information as possible.
2) There are three main types of data redundancy in images - coding, interpixel, and psychovisual - and compression aims to reduce one or more of these.
3) Popular lossless compression techniques, like Run Length Encoding and Huffman coding, exploit coding and interpixel redundancies. Lossy techniques introduce controlled loss for further compression.
notes_Image Compression_edited.ppt

Digital image compression techniques aim to reduce the number of bits required to represent an image by minimizing redundancy. There are two main categories: lossless compression preserves all image information while lossy compression provides higher data reduction but less than perfect image reproduction. Common methods include removing coding, interpixel, and psychovisual redundancies through techniques like variable length coding, discrete cosine transform, and quantization.
Reed Soloman and convolution codes

This document provides an overview of Reed-Solomon codes and convolutional codes. It describes the key properties and components of Reed-Solomon codes, including how they encode messages by dividing them into blocks and adding redundancy. It also explains convolutional codes use shift registers and linear algebraic functions to encode redundant information. The document compares block and convolutional codes and discusses factors like coding rate and constraint length that impact their performance.
Chapter 4 Lossless Compression Algorithims.pptx

Lossless compression algorithms compress data without any loss of information, allowing the original data to be perfectly reconstructed from the compressed data. Some common lossless compression algorithms include run length encoding (RLE), Huffman coding, Lempel-Ziv-Welch (LZW), and variable length coding (VLC). RLE replaces repeated characters with a single character and count, Huffman coding assigns variable length binary codes to characters based on their frequency, and LZW builds a dictionary of repeated strings to shorten repetitive sequences during compression. Lossless compression is useful for storage and transmission of files where preserving complete accuracy of the data is important.
Reed Solomon Coding For Error Detection and Correction

This document discusses Reed-Solomon coding for error detection and correction. It provides an overview of Reed-Solomon codes, including that they are a type of linear block code well-suited for correcting burst errors. The encoding and decoding processes are described at a high-level, involving the generation and root-finding of polynomials over Galois fields. Applications mentioned include data storage, satellite communications, barcodes, and CD audio. In summary, the document provides a technical introduction to Reed-Solomon coding, the encoding and decoding algorithms, and common uses in digital communication and storage systems.
M.TECH, ECE 2nd SEM LAB RECORD 

DFT and IDFT are verified on an RGB image. An RGB image is read from a file and converted to grayscale. The DFT is performed on the grayscale image and plotted. The IDFT is then performed on the DFT output and plotted, reconstructing the original grayscale image.
Digital image processing- Compression- Different Coding techniques 

Image Compression- Different coding Techniques such as Huffman coding, Bit plane and Arithmetic coding are discussed. By using these coding techniques compression of data or image can be achieved.
Lec_8_Image Compression.pdf

This document discusses various methods of image compression. It begins by defining image compression as reducing the amount of data required to represent a digital image. The main methods of compression are by removing redundant data from the image.
The document then discusses three main types of data redundancy that can be reduced: coding redundancy, spatial/temporal redundancy, and irrelevant information redundancy. Coding redundancy refers to inefficient coding of pixel values and can be reduced using techniques like Huffman coding or arithmetic coding. Spatial/temporal redundancy occurs from correlations between neighboring pixel values, while irrelevant information redundancy refers to data that is ignored by the human visual system.
The document provides examples and formulas for measuring compression ratio, data redundancy, and estimating the information content of
Lecft3data

Run-length encoding is a data compression technique that replaces consecutive repeating characters with the character and number of repeats. It can be used to compress text by replacing strings like "aabbcc" with "a2b2c2". For images, runs of pixels with the same intensity value are encoded as a pair of the run length and pixel value. Huffman coding assigns variable-length binary codes to symbols based on their frequency, with more common symbols getting shorter codes to compress data more efficiently than fixed-length codes.
art_sklar7_reed-solomon

1) Reed-Solomon codes are a type of error-correcting code invented in 1960 that can detect and correct multiple symbol errors. They work by encoding data into redundant symbols that can be used to detect and locate errors.
2) Reed-Solomon codes are particularly good at correcting burst errors, where a block of symbols are corrupted together by noise. Even if an entire block of bits is corrupted, the code can still correct the errors by replacing the corrupted symbol.
3) The error correction capability of Reed-Solomon codes increases with larger block sizes, as noise is averaged over more symbols. However, implementing Reed-Solomon codes also becomes more complex with higher redundancy.
art_sklar7_reed-solomon

1) Reed-Solomon codes are a type of error-correcting code invented in 1960 that can detect and correct multiple symbol errors. They work by encoding data into redundant symbols that can be used to detect and locate errors.
2) Reed-Solomon codes are particularly good at correcting burst errors, where a block of symbols are corrupted together by noise. Even if an entire block of bits is corrupted, the code can still correct the errors by replacing the corrupted symbol.
3) The error correction capability of Reed-Solomon codes increases with larger block sizes, as noise is averaged over more symbols. However, implementing Reed-Solomon codes also becomes more complex with higher redundancy.
art_sklar7_reed-solomon

1) Reed-Solomon codes are a type of error-correcting code invented in 1960 that can detect and correct multiple symbol errors. They work by encoding data into redundant symbols that can be used to detect and locate errors.
2) Reed-Solomon codes are particularly good at correcting burst errors, where a run of symbols are corrupted together, because they can correct a set number of errors regardless of where in the codeword they occur.
3) The error correction capability increases with lower code rates (more redundant symbols) and longer block lengths, as this averages the noise over more symbols and makes it less likely for a noise burst to corrupt too many consecutive symbols.
Compression

The document discusses different types of data compression techniques. It explains that compression reduces the size of data to reduce bandwidth and storage requirements when transmitting or storing audio, video, and images. It describes how compression works by exploiting redundancies in the data as well as properties of human perception. Various compression methods are outlined, including lossless techniques that preserve all information as well as lossy methods for audio and video that can tolerate some loss of information. Specific algorithms discussed include Huffman coding, run-length coding, LZW coding, and arithmetic coding. The document also provides details on JPEG image compression and MPEG video compression standards.
Compression

The document discusses different types of data compression techniques. It explains that compression reduces the size of data to reduce bandwidth and storage requirements when transmitting or storing audio, video, and images. It describes how compression works by exploiting redundancies in the data as well as properties of human perception. Various compression methods are outlined, including lossless techniques that preserve all information as well as lossy methods for audio and video that can tolerate some loss of information. Specific algorithms discussed include Huffman coding, run-length coding, LZW coding, and arithmetic coding. The document also provides details on JPEG image compression and MPEG video compression standards.
Error Detection N Correction

The document discusses error detection and correction techniques. It introduces Hamming codes, which can detect up to two bit errors and correct one bit errors. It explains how Hamming codes work by adding redundant parity bits to messages based on the values of data bits. A 4x7 generator matrix is used to encode 4-bit data words into 7-bit codewords for the Hamming(7,4) code. An example shows how a data word of 1010 encodes to the codeword 1011010. The summary then tests a C++ implementation of Hamming code encoding.
image compression in data compression

The document is a term paper on image compression submitted by a student. It discusses various topics related to image compression including:
- Introduction to image compression and its goals of reducing redundancy and storing/transmitting data efficiently.
- Methods to reduce correlation between pixels like predictive coding, orthogonal transforms, and subband coding.
- Quantization in image compression and its role in reducing less important high frequency components.
- Entropy coding techniques used in JPEG like differential coding, run-length coding, and Huffman coding to further compress the data.
12_HuffmanhsjsjsjjsiejjssjjejsjCoding_pdf.pdf

The document discusses data compression techniques including lossless and lossy compression. It focuses on Huffman coding, a lossless compression algorithm. It explains how Huffman coding works by assigning variable-length binary codes to characters based on their frequency, with more common characters getting shorter codes. This allows the data to be compressed. It provides an example showing the construction of a Huffman tree from character frequencies and the assignment of codes. The codes generated satisfy the prefix property to allow for unique decoding.
image compresson

This document discusses image compression techniques. It begins by explaining the goals of image compression which are to reduce storage requirements and increase transmission rates by decreasing the amount of data needed to represent a digital image. It then describes the main approaches of lossless and lossy compression as well as the tradeoff between image quality and compression ratio. The document goes on to explain various sources of redundancy in images like coding, interpixel, and psychovisual redundancy that compression aims to reduce. It also introduces concepts like entropy, data vs information, and different lossless compression methods including Huffman coding, arithmetic coding, LZW coding, DPCM, run-length coding, and bit-plane coding.
Similar to Compression Ii (20)
2.3 unit-ii-text-compression-a-outline-compression-techniques-run-length-codi...

2.3 unit-ii-text-compression-a-outline-compression-techniques-run-length-codi...
Reed Solomon Coding For Error Detection and Correction

Reed Solomon Coding For Error Detection and Correction
Digital image processing- Compression- Different Coding techniques 

Digital image processing- Compression- Different Coding techniques
More from anithabalaprabhu
Ch 04 Arithmetic Coding ( P P T)

Arithmetic coding is an entropy encoding technique that maps a sequence of symbols to a number between 0 and 1. Each possible sequence is assigned a unique interval within this range. As symbols are processed, the interval boundaries are updated based on the symbol probabilities. This allows arithmetic coding to efficiently encode sequences without needing to pre-determine codes for all possible sequences. It can achieve compression close to the entropy limit for long sequences, and easily supports adaptive and context modeling to handle non-IID sources. The interval updates ensure a unique number can be sent to decode the full sequence.
Datacompression1

The document discusses entropy and Shannon's first theorem. It defines entropy as the average amount of information received per symbol from a source where symbols have different probabilities. Entropy measures the uncertainty in the probability distribution of the source. The entropy of a source is equal to the minimum expected code length needed to encode symbols from that source.
Speech Compression

This document summarizes various audio compression techniques used to reduce the required storage space and transmission bandwidth for digital audio. It discusses lossless compression techniques that remove redundant data without degrading quality, as well as lossy techniques that remove inaudible or irrelevant information, resulting in smaller file sizes but some loss of quality. The key techniques described include psychoacoustic modeling to determine inaudible components, spectral analysis using transforms or filter banks, noise allocation to minimize quantization noise, and additional methods like predictive coding, coupling/delta encoding, and Huffman coding.
Z24 4 Speech Compression

The document discusses several speech compression techniques:
1) Uncompressed audio rates are 64kbps for voice and 1.5Mbps for CD audio.
2) ADPCM reduces the data rate to 32kbps by transmitting differences between predicted and actual sample values.
3) SB-ADPCM splits audio into lower and upper sub-bands, compressing each at different rates (48kbps and 16kbps respectively) for total of 64kbps.
4) LPC represents speech as a combination of previous samples and residual error, transmitting just coefficients, enabling lower rates like those in GSM and other standards.
Dictor

The document discusses different data compression techniques, focusing on lossless dictionary-based compression algorithms like Lempel-Ziv (LZ). It explains how LZ algorithms like LZW work by building an adaptive dictionary during compression and decompression. The LZW algorithm is described through examples. Advantages of LZW include no need to explicitly transfer the dictionary and fast encoding/decoding through table lookups. Problems like running out of dictionary space are also addressed.
Ch 04 Arithmetic Coding (Ppt)

Arithmetic coding is an entropy encoding technique that maps a sequence of symbols to a numeric interval between 0 and 1. Each symbol maps to a sub-interval of the current interval based on the symbol probabilities. As symbols are processed, the interval boundaries are updated according to the cumulative distribution function of the symbol probabilities. Arithmetic coding achieves better compression than Huffman coding by allowing coding of variable-length blocks without pre-specifying code lengths. It also handles conditional probability models more efficiently by updating interval boundaries based on context without needing pre-specified codebooks for all contexts.
06 Arithmetic 1

This document discusses arithmetic coding, an entropy encoding technique. It begins with an introduction comparing arithmetic coding to Huffman coding. The document then provides pseudocode for the basic encoding and decoding algorithms. It describes how scaling techniques like E1 and E2 scaling allow for incremental encoding and decoding as well as achieving infinite precision with finite-precision integers. The document outlines applications of arithmetic coding in areas like JBIG, H.264, and JPEG 2000.
Lassy

The document discusses lossy compression techniques. It begins by explaining that lossy compression algorithms compress data by discarding some information, yielding much higher compression ratios than lossless compression but resulting in distorted approximations of the original data. It then covers various lossy compression methods including quantization, transform coding using the discrete cosine transform (DCT), wavelet-based coding using the discrete wavelet transform (DWT), and techniques like vector quantization (VQ) and the Karhunen-Loeve transform (KLT) that aim to decorrelate signal components before quantization. Key aspects like rate-distortion theory, various distortion measures, and algorithms for quantization are also described.
Compression Ii

The document discusses various image compression techniques including:
1) Variable length coding such as Huffman coding which reduces redundancy but is not optimal for the sample image due to inter-pixel redundancy.
2) Predictive coding which encodes pixel differences to remove redundancy, achieving higher compression ratios.
3) Lossy techniques like JPEG use quantization and discrete cosine transform to compress images further, introducing some distortion.
Lossy

The document discusses lossy compression techniques such as quantization and transform coding. It explains that lossy compression achieves higher compression rates by introducing some loss or distortion to the reconstructed data compared to the original. It describes various distortion measures used to evaluate the quality of lossy compression, including mean squared error and peak signal-to-noise ratio. It also discusses the discrete cosine transform, a widely used transform coding technique that decomposes images or signals into different frequency components for more efficient compression.
Planning

The document discusses various aspects of project planning and control, including defining control variables, product/process/resource characteristics, different control situations, and techniques for project planning and control. It covers archetypical control situations like realization, allocation, design, and exploration problems. Risk management strategies are also summarized, including identifying risk factors, determining risk exposure, and developing risk mitigation strategies.
Losseless

This document discusses lossless data compression and introduces key concepts such as codecs, prefix codes, entropy, and Shannon's source coding theorem. Specifically:
- Lossless data compression allows for perfect retrieval of original files by storing/transmitting big files using fewer bytes, with examples like ZIP files.
- A codec consists of a coder that maps messages to codewords and a decoder that maps codewords back to the original messages. Prefix codes are codes where no codeword is a prefix of another.
- Entropy measures the uncertainty in a probabilistic source, with the entropy of a distribution being the expected self-entropy of messages drawn from that distribution.
- Shannon's source coding theorem states that the expected
Lec32

The document discusses Huffman coding, a lossless data compression algorithm that uses variable-length codewords to encode symbols based on their frequency of occurrence. It works by building a binary tree from the frequency of symbols, where more frequent symbols are encoded by shorter codewords. This allows for more efficient representation of frequent symbols and achieves compression close to the theoretical minimum possible given the frequencies. The algorithm and encoding/decoding process are explained step-by-step with an example.
Lec5 Compression

1. The document discusses different compression techniques for text, audio, images, and video.
2. It provides examples of compression ratios achieved using lossy and lossless compression methods. For example, text compression can achieve 3:1 ratios using Lempel-Ziv coding while audio compression can achieve ratios between 3:1 to 24:1 using MP3.
3. The techniques discussed include entropy encoding, run-length encoding, Huffman coding, discrete cosine transforms, and differential encoding which takes advantage of redundancies in the data. The best approach depends on the type of data and acceptable quality.
Huffman Student

The document discusses Huffman coding, which is a variable-length binary coding technique used for lossless data compression. It describes how Huffman codes are constructed using a Huffman tree to assign codewords to symbols based on their frequency of occurrence, with more frequent symbols assigned shorter codewords. The document outlines the Huffman coding algorithm and provides examples of how it works to generate an optimal prefix code with the minimum average codeword length.
Huffman Encoding Pr

Huffman encoding is a variable-length encoding technique used for text compression that assigns shorter bit strings to more common characters and longer bit strings to less common characters. It uses a prefix code where no codeword is a prefix of another, allowing for unique decoding. The algorithm works by building a Huffman tree from the bottom up by repeatedly combining the two lowest frequency symbols into a node until a full tree is created, with codes read from the paths. This greedy approach results in an optimal prefix code that minimizes the expected codeword length, improving compression.
Huffman1

Huffman coding is a data compression technique that uses variable-length code words to encode characters based on their frequency of occurrence. It involves building a Huffman tree from the character frequencies, where more common characters are encoded with shorter code words. The tree is then traversed to assign each character a unique code. The encoded file is smaller since frequent characters take up less bits. It works well for text files since letters are non-uniformly distributed.
Huffman

Huffman coding is a data compression technique that uses statistical coding to assign variable-length code words to characters based on their frequency of occurrence. It involves building a Huffman tree from character frequencies, where more common characters have shorter code words. The encoded file is then created by traversing the tree to assign each character its code word. This results in a smaller file size than other fixed-length encodings like ASCII.
More from anithabalaprabhu (18)
Recently uploaded
zkStudyClub - Reef: Fast Succinct Non-Interactive Zero-Knowledge Regex Proofs

This paper presents Reef, a system for generating publicly verifiable succinct non-interactive zero-knowledge proofs that a committed document matches or does not match a regular expression. We describe applications such as proving the strength of passwords, the provenance of email despite redactions, the validity of oblivious DNS queries, and the existence of mutations in DNA. Reef supports the Perl Compatible Regular Expression syntax, including wildcards, alternation, ranges, capture groups, Kleene star, negations, and lookarounds. Reef introduces a new type of automata, Skipping Alternating Finite Automata (SAFA), that skips irrelevant parts of a document when producing proofs without undermining soundness, and instantiates SAFA with a lookup argument. Our experimental evaluation confirms that Reef can generate proofs for documents with 32M characters; the proofs are small and cheap to verify (under a second).
Paper: https://eprint.iacr.org/2023/1886
GraphSummit Singapore | The Art of the Possible with Graph - Q2 2024

Neha Bajwa, Vice President of Product Marketing, Neo4j
Join us as we explore breakthrough innovations enabled by interconnected data and AI. Discover firsthand how organizations use relationships in data to uncover contextual insights and solve our most pressing challenges – from optimizing supply chains, detecting fraud, and improving customer experiences to accelerating drug discoveries.
Securing your Kubernetes cluster_ a step-by-step guide to success !

Today, after several years of existence, an extremely active community and an ultra-dynamic ecosystem, Kubernetes has established itself as the de facto standard in container orchestration. Thanks to a wide range of managed services, it has never been so easy to set up a ready-to-use Kubernetes cluster.
However, this ease of use means that the subject of security in Kubernetes is often left for later, or even neglected. This exposes companies to significant risks.
In this talk, I'll show you step-by-step how to secure your Kubernetes cluster for greater peace of mind and reliability.
Goodbye Windows 11: Make Way for Nitrux Linux 3.5.0!

As the digital landscape continually evolves, operating systems play a critical role in shaping user experiences and productivity. The launch of Nitrux Linux 3.5.0 marks a significant milestone, offering a robust alternative to traditional systems such as Windows 11. This article delves into the essence of Nitrux Linux 3.5.0, exploring its unique features, advantages, and how it stands as a compelling choice for both casual users and tech enthusiasts.
20240605 QFM017 Machine Intelligence Reading List May 2024

Everything I found interesting about machines behaving intelligently during May 2024
“I’m still / I’m still / Chaining from the Block”

“An Outlook of the Ongoing and Future Relationship between Blockchain Technologies and Process-aware Information Systems.” Invited talk at the joint workshop on Blockchain for Information Systems (BC4IS) and Blockchain for Trusted Data Sharing (B4TDS), co-located with with the 36th International Conference on Advanced Information Systems Engineering (CAiSE), 3 June 2024, Limassol, Cyprus.
Artificial Intelligence for XMLDevelopment

In the rapidly evolving landscape of technologies, XML continues to play a vital role in structuring, storing, and transporting data across diverse systems. The recent advancements in artificial intelligence (AI) present new methodologies for enhancing XML development workflows, introducing efficiency, automation, and intelligent capabilities. This presentation will outline the scope and perspective of utilizing AI in XML development. The potential benefits and the possible pitfalls will be highlighted, providing a balanced view of the subject.
We will explore the capabilities of AI in understanding XML markup languages and autonomously creating structured XML content. Additionally, we will examine the capacity of AI to enrich plain text with appropriate XML markup. Practical examples and methodological guidelines will be provided to elucidate how AI can be effectively prompted to interpret and generate accurate XML markup.
Further emphasis will be placed on the role of AI in developing XSLT, or schemas such as XSD and Schematron. We will address the techniques and strategies adopted to create prompts for generating code, explaining code, or refactoring the code, and the results achieved.
The discussion will extend to how AI can be used to transform XML content. In particular, the focus will be on the use of AI XPath extension functions in XSLT, Schematron, Schematron Quick Fixes, or for XML content refactoring.
The presentation aims to deliver a comprehensive overview of AI usage in XML development, providing attendees with the necessary knowledge to make informed decisions. Whether you’re at the early stages of adopting AI or considering integrating it in advanced XML development, this presentation will cover all levels of expertise.
By highlighting the potential advantages and challenges of integrating AI with XML development tools and languages, the presentation seeks to inspire thoughtful conversation around the future of XML development. We’ll not only delve into the technical aspects of AI-powered XML development but also discuss practical implications and possible future directions.
GDG Cloud Southlake #33: Boule & Rebala: Effective AppSec in SDLC using Deplo...

Effective Application Security in Software Delivery lifecycle using Deployment Firewall and DBOM
The modern software delivery process (or the CI/CD process) includes many tools, distributed teams, open-source code, and cloud platforms. Constant focus on speed to release software to market, along with the traditional slow and manual security checks has caused gaps in continuous security as an important piece in the software supply chain. Today organizations feel more susceptible to external and internal cyber threats due to the vast attack surface in their applications supply chain and the lack of end-to-end governance and risk management.
The software team must secure its software delivery process to avoid vulnerability and security breaches. This needs to be achieved with existing tool chains and without extensive rework of the delivery processes. This talk will present strategies and techniques for providing visibility into the true risk of the existing vulnerabilities, preventing the introduction of security issues in the software, resolving vulnerabilities in production environments quickly, and capturing the deployment bill of materials (DBOM).
Speakers:
Bob Boule
Robert Boule is a technology enthusiast with PASSION for technology and making things work along with a knack for helping others understand how things work. He comes with around 20 years of solution engineering experience in application security, software continuous delivery, and SaaS platforms. He is known for his dynamic presentations in CI/CD and application security integrated in software delivery lifecycle.
Gopinath Rebala
Gopinath Rebala is the CTO of OpsMx, where he has overall responsibility for the machine learning and data processing architectures for Secure Software Delivery. Gopi also has a strong connection with our customers, leading design and architecture for strategic implementations. Gopi is a frequent speaker and well-known leader in continuous delivery and integrating security into software delivery.
GraphSummit Singapore | The Future of Agility: Supercharging Digital Transfor...

Leonard Jayamohan, Partner & Generative AI Lead, Deloitte
This keynote will reveal how Deloitte leverages Neo4j’s graph power for groundbreaking digital twin solutions, achieving a staggering 100x performance boost. Discover the essential role knowledge graphs play in successful generative AI implementations. Plus, get an exclusive look at an innovative Neo4j + Generative AI solution Deloitte is developing in-house.
Encryption in Microsoft 365 - ExpertsLive Netherlands 2024

In this session I delve into the encryption technology used in Microsoft 365 and Microsoft Purview. Including the concepts of Customer Key and Double Key Encryption.
How to Get CNIC Information System with Paksim Ga.pptx

Pakdata Cf is a groundbreaking system designed to streamline and facilitate access to CNIC information. This innovative platform leverages advanced technology to provide users with efficient and secure access to their CNIC details.
Mind map of terminologies used in context of Generative AI

Mind map of common terms used in context of Generative AI.
GridMate - End to end testing is a critical piece to ensure quality and avoid...

End to end testing is a critical piece to ensure quality and avoid regressions. In this session, we share our journey building an E2E testing pipeline for GridMate components (LWC and Aura) using Cypress, JSForce, FakerJS…
Epistemic Interaction - tuning interfaces to provide information for AI support

Paper presented at SYNERGY workshop at AVI 2024, Genoa, Italy. 3rd June 2024
https://alandix.com/academic/papers/synergy2024-epistemic/
As machine learning integrates deeper into human-computer interactions, the concept of epistemic interaction emerges, aiming to refine these interactions to enhance system adaptability. This approach encourages minor, intentional adjustments in user behaviour to enrich the data available for system learning. This paper introduces epistemic interaction within the context of human-system communication, illustrating how deliberate interaction design can improve system understanding and adaptation. Through concrete examples, we demonstrate the potential of epistemic interaction to significantly advance human-computer interaction by leveraging intuitive human communication strategies to inform system design and functionality, offering a novel pathway for enriching user-system engagements.
LF Energy Webinar: Electrical Grid Modelling and Simulation Through PowSyBl -...

Do you want to learn how to model and simulate an electrical network from scratch in under an hour?
Then welcome to this PowSyBl workshop, hosted by Rte, the French Transmission System Operator (TSO)!
During the webinar, you will discover the PowSyBl ecosystem as well as handle and study an electrical network through an interactive Python notebook.
PowSyBl is an open source project hosted by LF Energy, which offers a comprehensive set of features for electrical grid modelling and simulation. Among other advanced features, PowSyBl provides:
- A fully editable and extendable library for grid component modelling;
- Visualization tools to display your network;
- Grid simulation tools, such as power flows, security analyses (with or without remedial actions) and sensitivity analyses;
The framework is mostly written in Java, with a Python binding so that Python developers can access PowSyBl functionalities as well.
What you will learn during the webinar:
- For beginners: discover PowSyBl's functionalities through a quick general presentation and the notebook, without needing any expert coding skills;
- For advanced developers: master the skills to efficiently apply PowSyBl functionalities to your real-world scenarios.
20240609 QFM020 Irresponsible AI Reading List May 2024

Everything I found interesting about the irresponsible use of machine intelligence in May 2024
Removing Uninteresting Bytes in Software Fuzzing

Imagine a world where software fuzzing, the process of mutating bytes in test seeds to uncover hidden and erroneous program behaviors, becomes faster and more effective. A lot depends on the initial seeds, which can significantly dictate the trajectory of a fuzzing campaign, particularly in terms of how long it takes to uncover interesting behaviour in your code. We introduce DIAR, a technique designed to speedup fuzzing campaigns by pinpointing and eliminating those uninteresting bytes in the seeds. Picture this: instead of wasting valuable resources on meaningless mutations in large, bloated seeds, DIAR removes the unnecessary bytes, streamlining the entire process.
In this work, we equipped AFL, a popular fuzzer, with DIAR and examined two critical Linux libraries -- Libxml's xmllint, a tool for parsing xml documents, and Binutil's readelf, an essential debugging and security analysis command-line tool used to display detailed information about ELF (Executable and Linkable Format). Our preliminary results show that AFL+DIAR does not only discover new paths more quickly but also achieves higher coverage overall. This work thus showcases how starting with lean and optimized seeds can lead to faster, more comprehensive fuzzing campaigns -- and DIAR helps you find such seeds.
- These are slides of the talk given at IEEE International Conference on Software Testing Verification and Validation Workshop, ICSTW 2022.
Recently uploaded (20)
zkStudyClub - Reef: Fast Succinct Non-Interactive Zero-Knowledge Regex Proofs

zkStudyClub - Reef: Fast Succinct Non-Interactive Zero-Knowledge Regex Proofs
GraphSummit Singapore | The Art of the Possible with Graph - Q2 2024

GraphSummit Singapore | The Art of the Possible with Graph - Q2 2024
Securing your Kubernetes cluster_ a step-by-step guide to success !

Securing your Kubernetes cluster_ a step-by-step guide to success !
Goodbye Windows 11: Make Way for Nitrux Linux 3.5.0!

Goodbye Windows 11: Make Way for Nitrux Linux 3.5.0!
20240605 QFM017 Machine Intelligence Reading List May 2024

20240605 QFM017 Machine Intelligence Reading List May 2024
GDG Cloud Southlake #33: Boule & Rebala: Effective AppSec in SDLC using Deplo...

GDG Cloud Southlake #33: Boule & Rebala: Effective AppSec in SDLC using Deplo...
GraphSummit Singapore | The Future of Agility: Supercharging Digital Transfor...

GraphSummit Singapore | The Future of Agility: Supercharging Digital Transfor...
Monitoring Java Application Security with JDK Tools and JFR Events

Monitoring Java Application Security with JDK Tools and JFR Events
Encryption in Microsoft 365 - ExpertsLive Netherlands 2024

Encryption in Microsoft 365 - ExpertsLive Netherlands 2024
How to Get CNIC Information System with Paksim Ga.pptx

How to Get CNIC Information System with Paksim Ga.pptx
Mind map of terminologies used in context of Generative AI

Mind map of terminologies used in context of Generative AI
GridMate - End to end testing is a critical piece to ensure quality and avoid...

GridMate - End to end testing is a critical piece to ensure quality and avoid...
Epistemic Interaction - tuning interfaces to provide information for AI support

Epistemic Interaction - tuning interfaces to provide information for AI support
LF Energy Webinar: Electrical Grid Modelling and Simulation Through PowSyBl -...

LF Energy Webinar: Electrical Grid Modelling and Simulation Through PowSyBl -...
20240609 QFM020 Irresponsible AI Reading List May 2024

20240609 QFM020 Irresponsible AI Reading List May 2024
Compression Ii
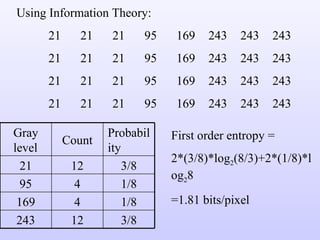
- 1. Using Information Theory: 21 21 21 95 169 243 243 243 21 21 21 95 169 243 243 243 21 21 21 95 169 243 243 243 21 21 21 95 169 243 243 243 First order entropy = 2*(3/8)*log 2 (8/3)+2*(1/8)*log 2 8 =1.81 bits/pixel Gray level Count Probability 21 12 3/8 95 4 1/8 169 4 1/8 243 12 3/8
- 2. Second-order entropy = 2*(1/4)*log 2 4+4*(1/8)*log 2 8=1+1.5=2.5 bits/pair = 1.25 bits/pixel. Gray level pair Count Probability (21,21) 8 ¼ (21,95) 4 1/8 (95,169) 4 1/8 (169,243) 4 1/8 (243,243) 8 ¼ (243,21) 4 1/8
- 3. The fact that the second order entropy (in bits/pixel) is less than the first order entropy, indicates the presence of inter-pixel redundancy. Hence variable length coding alone will not lead to the most optimum compression in this case. Consider mapping the pixels of the image to create the following representation: 21 0 0 74 74 74 0 0 21 0 0 74 74 74 0 0 21 0 0 74 74 74 0 0 21 0 0 74 74 74 0 0
- 4. Here, we construct a difference array by replicating the first column of the original image and using the arithmetic difference between adjacent columns for the remaining elements. First order entropy of this difference image = 1.41 bits/pixel Gray level or difference Count Probability 0 16 ½ 21 4 1/8 74 12 3/8
- 5. Near optimal variable length codes: Huffman codes require an enormous number of computations. For N source symbols, N-2 source reductions (sorting operations) and N-2 code assignments must be made. Sometimes we sacrifice coding efficiency for reducing the number of computations.
- 8. Truncated Huffman code: A truncated Huffman code is generated by Huffman coding only the most probable M symbols of the source, for some integer M (less than the total N symbols). A prefix code followed by a suitable fixed length is used to represent all other source symbols. In the table in the previous slide, M was arbitrarily selected as 12 and the prefix code was generated as the 13 th Huffman code word. That is a 13 th symbol whose probability is the sum of the probabilities of the symbols from 13 th to 21 st is included in the Huffman coding along with the first 12 symbols.
- 9. B-code: It is close to optimal when the source symbols probabilities obey a law of the form: P(a j ) = c j - In the B-code, each code word is made up of continuation bits, denoted C, and information bits, which are binary numbers. The only purpose of the continuation bits is to separate individual code words, so they simply toggle between 0 and 1 for each new code word. The B-code shown here is called a B 2 code, because two information bits are used per continuation bit.
- 12. Arithmetic coding: Unlike the variable-length codes described previously, arithmetic coding , generates non-block codes. In arithmetic coding, a one-to-one correspondence between source symbols and code words does not exist. Instead, an entire sequence of source symbols (or message) is assigned a single arithmetic code word. The code word itself defines an interval of real numbers between 0 and 1. As the number of symbols in the message increases, the interval used to represent it becomes smaller and the number of information units (say, bits) required to represent the interval becomes larger. Each symbol of the message reduces the size of the interval in accordance with the probability of occurrence. It is supposed to approach the limit set by entropy.
- 13. Arithmetic coding Let the message to be encoded be a 1 a 2 a 3 a 3 a 4
- 14. 0.2 0.4 0.8 0.04 0.08 0.16 0.048 0.056 0.072 0.0592 0.0624 0.0688 0.06368 0.06496
- 15. So, any number in the interval [0.06752,0.0688) , for example 0.068 can be used to represent the message. Here 3 decimal digits are used to represent the 5 symbol source message. This translates into 3/5 or 0.6 decimal digits per source symbol and compares favourably with the entropy of -(3x0.2log 10 0.2+0.4log 10 0.4) = 0.5786 digits per symbol
- 17. 1.0 0.8 0.4 0.2 0.8 0.72 0.56 0.48 0.4 0.0 0.72 0.688 0.624 0.592 0.592 0.5856 0.5728 0.5664 Therefore, the message is a 3 a 3 a 1 a 2 a 4 0.5728 0.57152 056896 0.56768 Decoding: Decode 0.572. Since 0.8>code word > 0.4, the first symbol should be a 3 . 0.56 0.56 0.5664
- 20. Example: 39 39 126 126 39 39 126 126 39 39 126 126 39 39 126 126
- 24. Recognized Encoded value pixels Dic. address Dic. entry 39 39 39 39 39 256 39-39 39 126 126 257 39-126 126 126 126 258 126-126 126 256 39-39 259 126-39 256 258 126-126 260 39-39-126 258 260 39-39-126 261 126-126-39 260 259 126-39 262 39-39-126-126 259 257 39-126 263 126-39-39 257 126 126 264 39-126-126
- 25. INTERPIXEL REDUNDANCY Variable length coding will produce identical compression ratios for the two images shown on the next slide, however we can achieve higher compression ratios by reducing interpixel redundancy. We can detect the presence of correlation between pixels (or interpixel redundancy) by computing the auto-correlation coefficients along a row of pixels
- 26. Maximum possible value of n) is 1 and this value is approached for this image, both for adjacent pixels and also for pixels which are separated by 45 pixels (or multiples of 45).
- 27. Chapter 8 Image Compression
- 31. An m-bit gray scale image can be converted into m binary images by bit-plane slicing. These individual images are then encoded using run-length coding. However, a small difference in the gray level of adjacent pixels can cause a disruption of the run of zeroes or ones. Eg: Let us say one pixel has a gray level of 127 and the next pixel has a gray level of 128. In binary: 127 = 01111111 & 128 = 10000000 Therefore a small change in gray level has decreased the run-lengths in all the bit-planes!
- 33. Let g m-1 …….g 1 g 0 represent the gray code representation of a binary number. Then: In gray code: 127 = 01000000 128 = 11000000
- 37. Decoding a gray coded image: The MSB is retained as such,i.e.,
- 40. Decompression: Most general form : Most Simple form
- 41. Example for Lossless Predictive coding
- 44. Delta modulation (DM) is a well-known form of lossy predictive coding in which the predictor and quantizer are defined as:
- 45. DELTA MODULATION
- 48. TRANSFORM CODING
- 51. Zig-zag coding is done after the quantization as shown below 4333222122200000 4.32 3.12 3.01 2.41 2.74 2.11 1.92 1.55 2.11 1.33 0.32 0.11 1.62 0.44 0.03 0.02 0 0 0 2 0 0 1 2 2 2 2 3 2 3 3 4