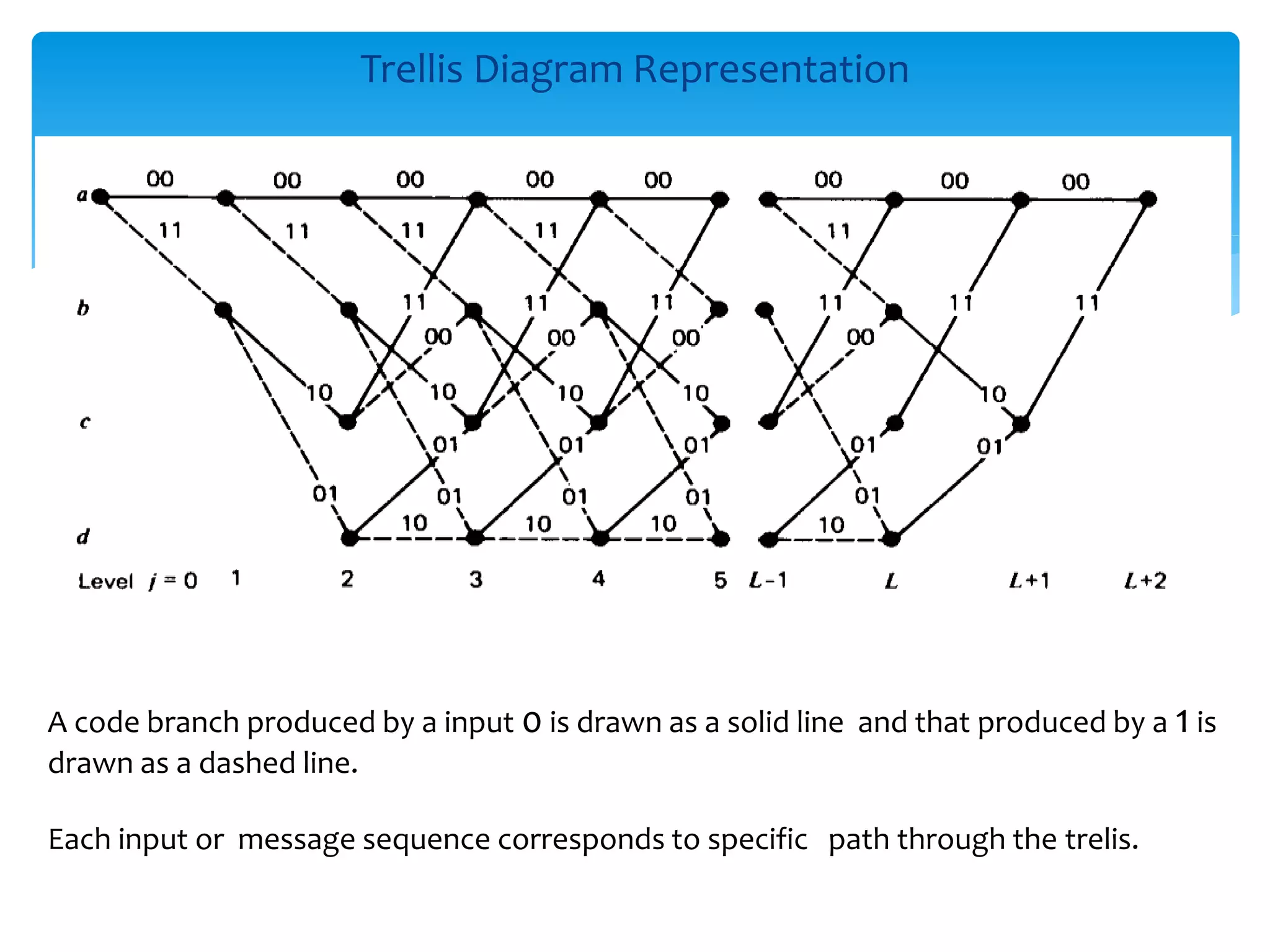
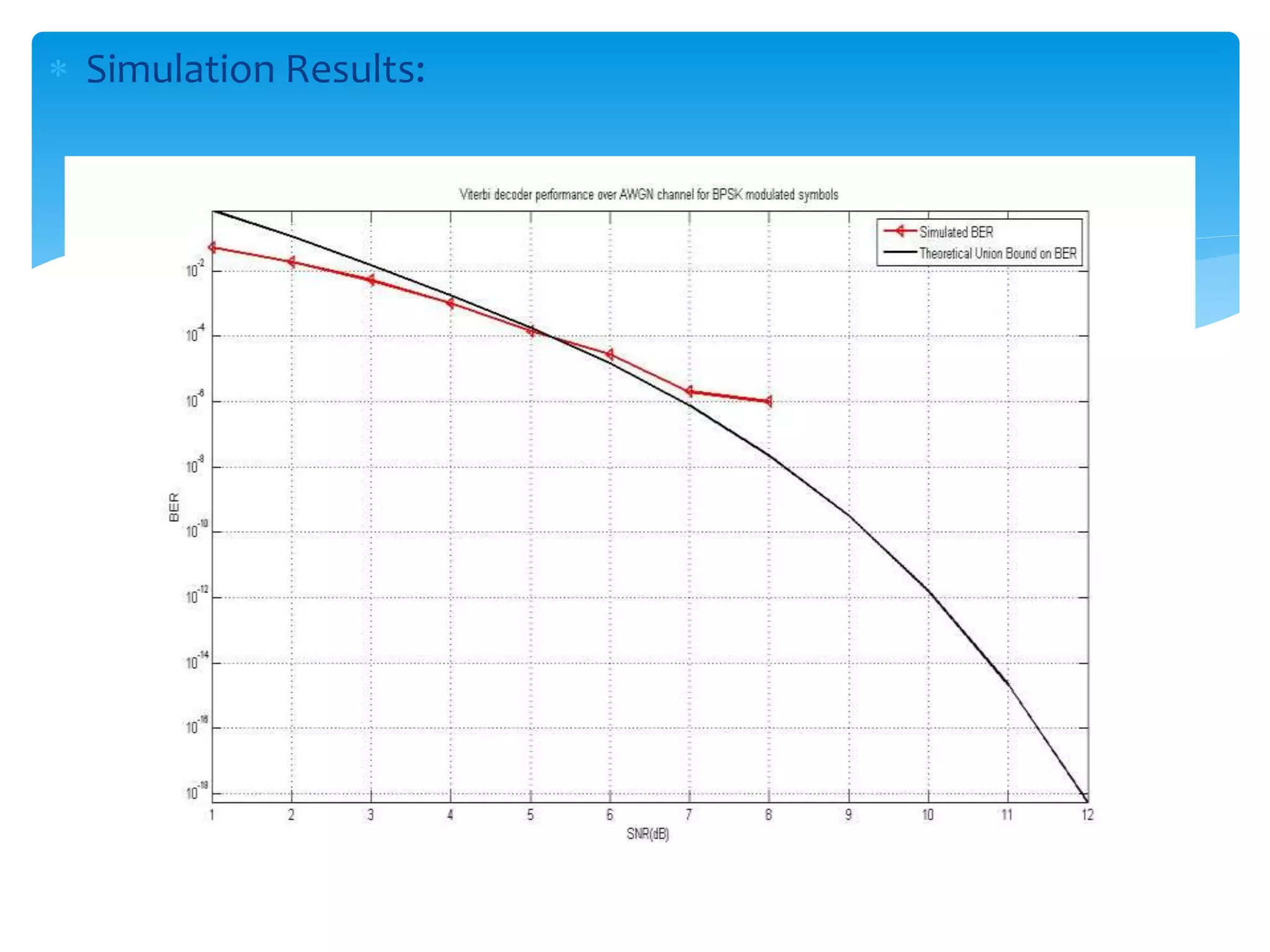
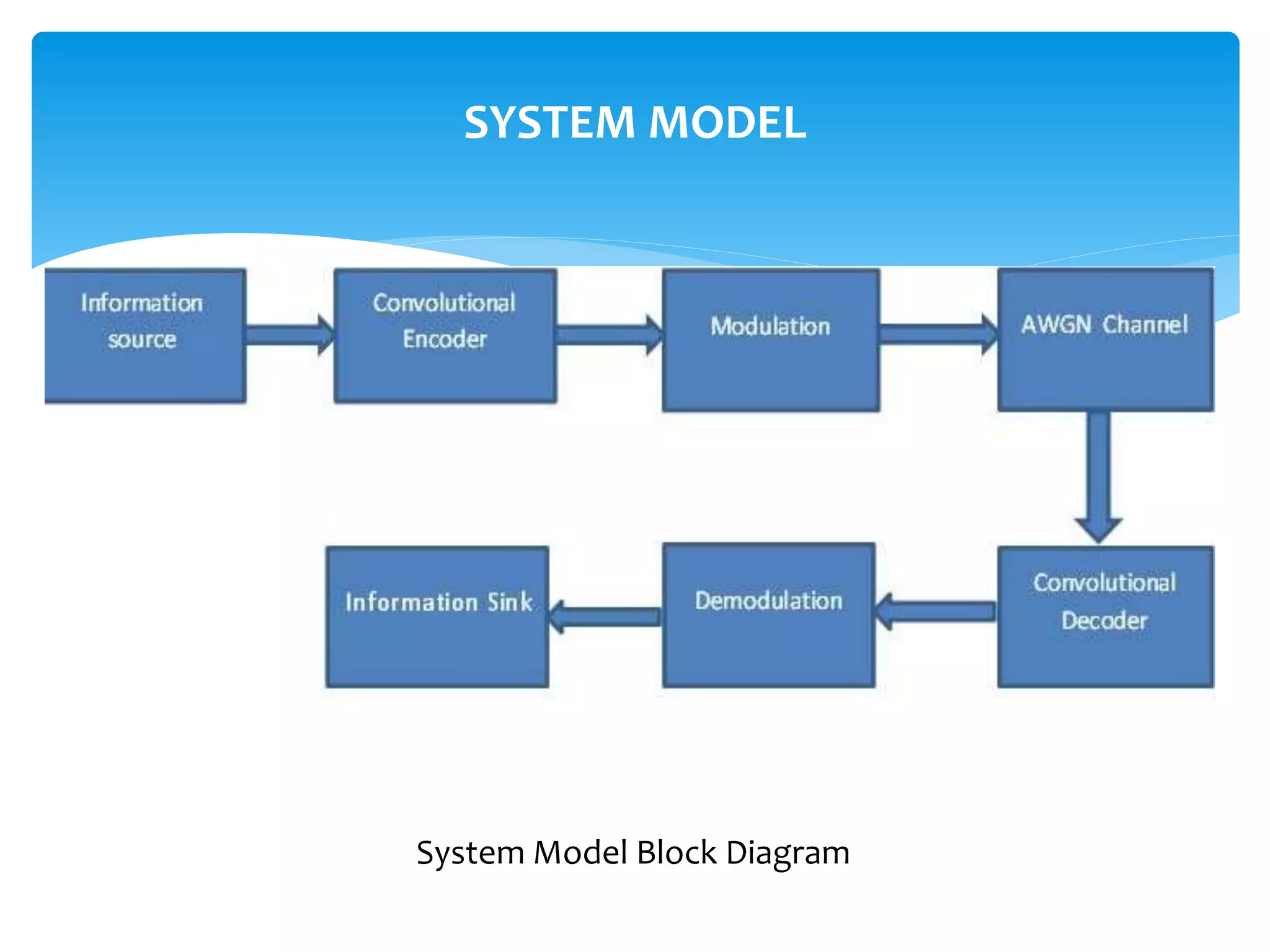
This document describes convolutional codes for channel coding in communication systems. Convolutional codes are represented by parameters like constraint length K, where K is the number of shift registers used. The convolutional encoder operates like a finite state machine, with the state defined by the most recent K-1 message bits. The trellis diagram provides an explicit representation of the convolutional encoder as a finite state machine. Convolutional codes are decoded using the Viterbi algorithm, which performs maximum likelihood decoding by selecting the most probable path through the trellis. Simulation results show the performance of the convolutional encoding and decoding system.

1. Implementation of Convolutional
Encoder and Decoder
BY-RONIT KUMAR
111EC0175

2. INTRODUCTION
• Maintenance of the quality of data is the most important thing
in communication. There are various factors that affect the
quality of data when it is transferred over a communication
channel like noise, fading etc.
• To overcome these effects channel coding schemes are
introduced.
• In this presentation one type of channel coding is described
which is Convolutional Codes

3. Why Channel Coding?
• In digital communication systems to improve the quality of data
at output, channel coding is employed. It deals with various
numbers of techniques that are being used for the
improvement of performance of our communication system
• It increases the information transfer rate at a fixed error rate or
error rate can be reduced with a fixed information transfer rate.
• The maximum performance of the system is restricted by
Shannon limit.

4. Convolutional codes
 Convolutional codes are represented by three parameters n, k,
K. where K represents the number of shift registers used in the
encoding part .
 The coded sequence of n bits obtained after encoding not only
depends on the k bit information message but also on the
previous information bits that is transmitted.
 Convolutional codes are same as block codes but encoder has
an additional structure.
 Convolutional code is a linear code and its mapping is bijective.

5. SYSTEM MODEL
System Model Block Diagram

6.  A sequence of message bits is used as data source
Convolutional coding is applied on the binary data . After
encoding of image, modulation is performed.
 Additive White Gaussian Noise (AWGN) is added when this
coded data is passed through the channel. This noise
changes/flips some of the data bits.
 Convolutional decoding of the received sequence is performed
at the receiver end. After decoding is demodulation is done and
original transmitted message is retrieved.

7. Description of a convolutional encoder

8. • It has constraint length 3 and because two adders are used in it
its rate is ½.
• A bit is shifted into the leftmost stage at each input and the
bits previously existing in the shift registers are shifted one
position to right.
• After applying the modulo-2 operation corresponding
outputs are obtained. This process continues until the arrival of
data at the input of encoder.
• The choice of connection between the shift registers and
adders describes the characteristics of code. By varying the
connections, characteristics of the code can be varied.

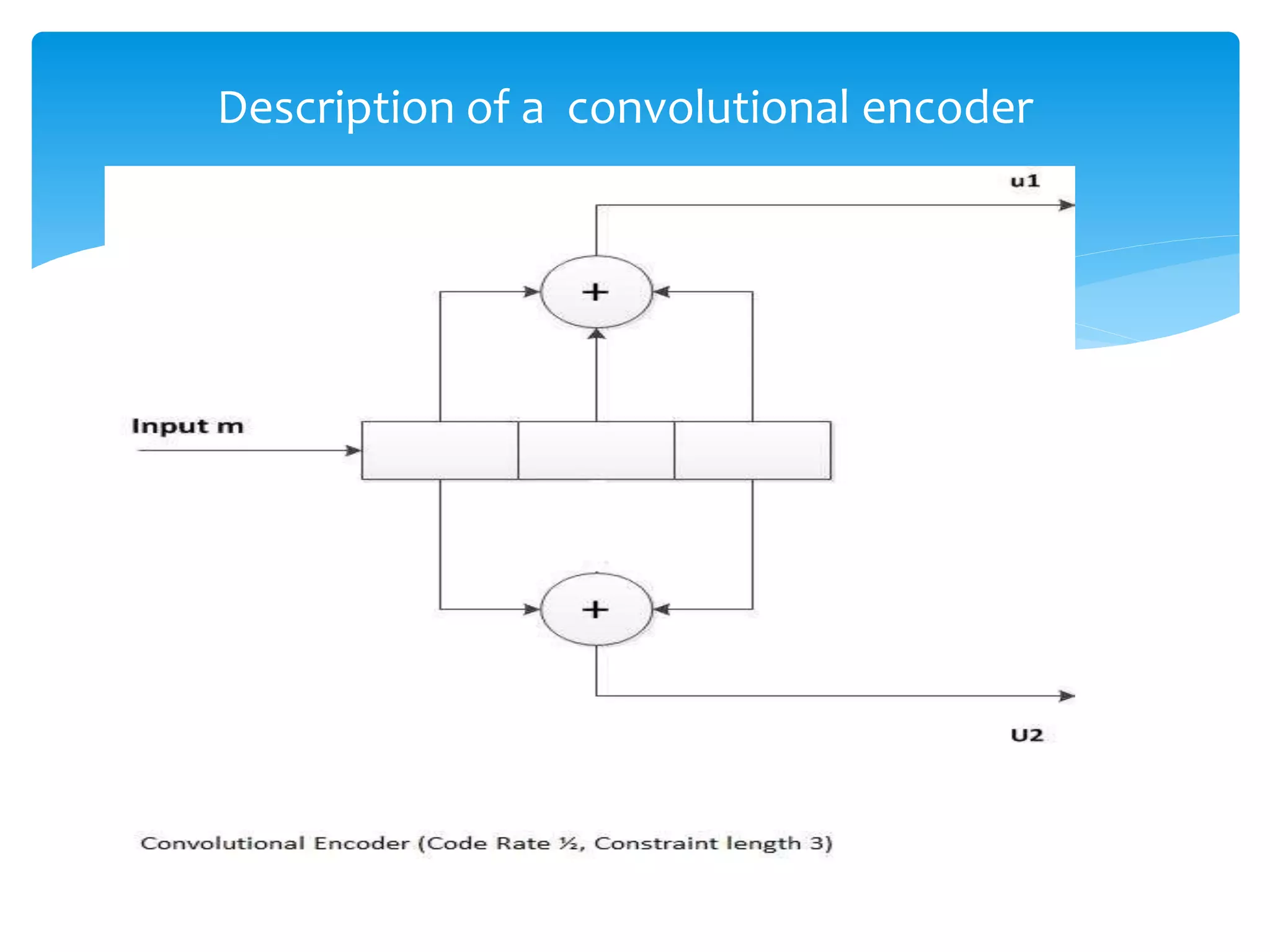
9. • To describe an encoder, set of “m” connection vectors are required.
These vectors have the same dimension as that of K (shift registers).
These connections describe which shift register is connected with m
adders.
• A value of “1” in the position demonstrates that, that shift register is
connected to the adder and a “0” in given position will indicate that
not a single connection exits between the stage and adder.
• For encoder shown in Fig. we can write the connection vector for
upper connection and for lower connection as follows:
h1=[1 1 1]…………..(1)
h2=[1 0 1]…………..(2)

10. Trellis Diagram Representation
A code branch produced by a input 0 is drawn as a solid line and that produced by a 1 is
drawn as a dashed line.
Each input or message sequence corresponds to specific path through the trelis.

11.  It explicitly brings out the fact that the convolutional encoder is
a finite state machine.
 The state of a convolutional encoder of rate 1/n is defined as
the most recent (K-1) message bits moved into the encoder’s
shift register.
 So at time j the state of the encoder is (mj-K+1,mj-K+2,….mj-1,mj)
 The trellis contains (L+K) levels where L is the length of the
message sequence and K is the constraint length of the code.

12. The Viterbi Algorithm(Decoding of convolutional codes)
 The viterbi algorithm is used to decode convolutional codes and any
structure or system that can be described by a trellis.
 It is a maximum likelihood decoding algorithm that selects the most
probable path that maximizes the likelihood function.
 The algorithm is based on add-compare-select the best path each time at
each state.
 The steps are :
1.Walk through the trellis and compute the Hamming distance between
that branch of r and those in the trellis.

13. 2.At each level, consider the two paths entering the same node
and are identical from this node onwards. From these two paths,
the one that is closer to r at this stage will still be so at any time in
the future. This path is retained, and the other path is discarded.
3.Proceeding this way, at each stage one path will be saved for
each node. These paths are called the survivors. The decoded
sequence (based on Minimum distance Decoding) is guaranteed
to be one of these survivors.
4.Each survivor is associated with a metric of the accumulated
Hamming distance (the Hamming distance up to this stage).
5.Carry out this process until the received sequence is considered
completely. Choose the survivor with the smallest metric.

14.  Simulation Results:

15. FUTURE WORK
 VHDL Implementation of convolutional encoding and decoding
 To improve performance by finding and implementing better
coding techniques.
References:
 Digital Communication By Simon Haykins
 IEEE Papers on Convolutional Coding and Decoding
 Google

16. THANK YOU