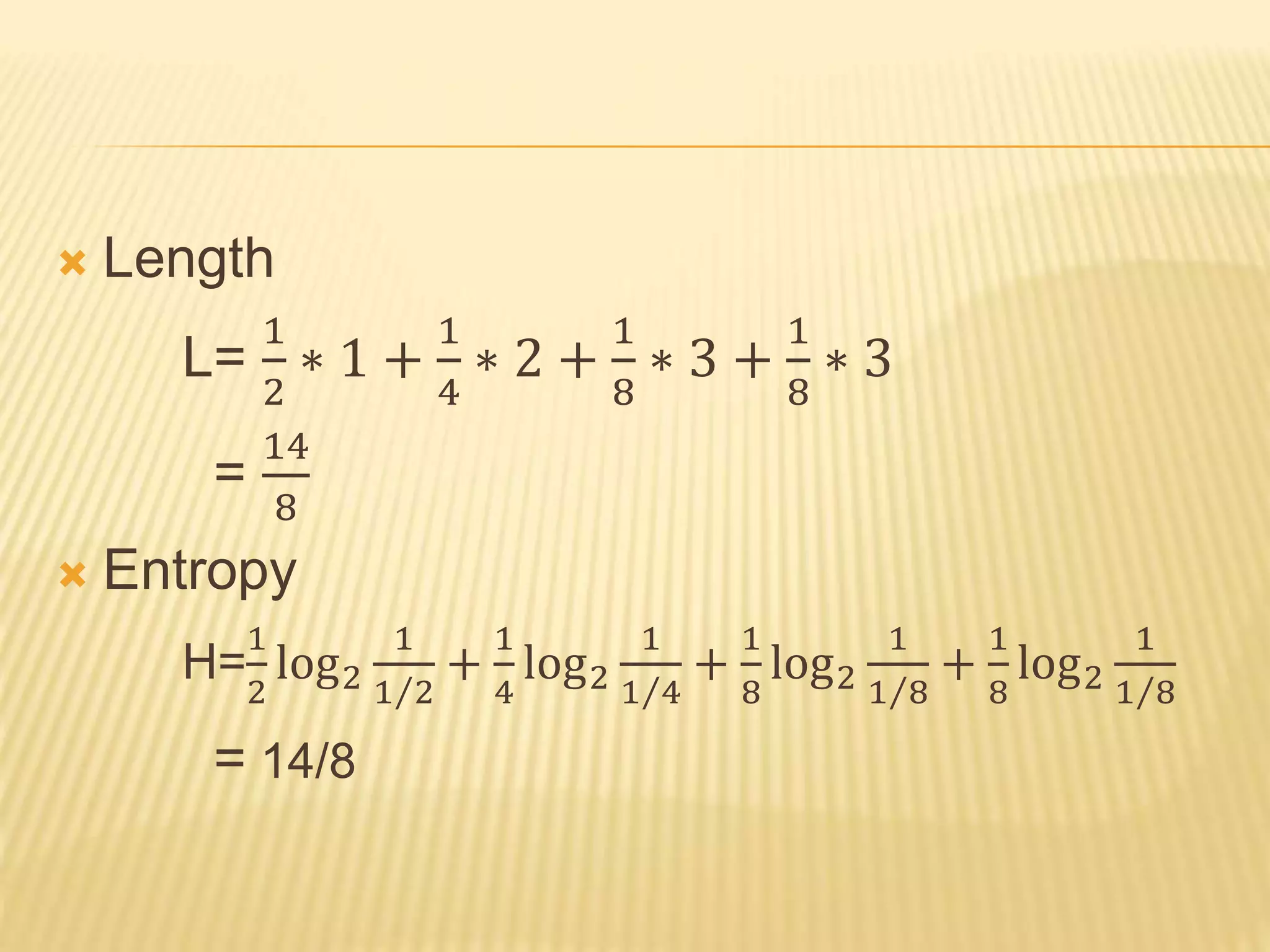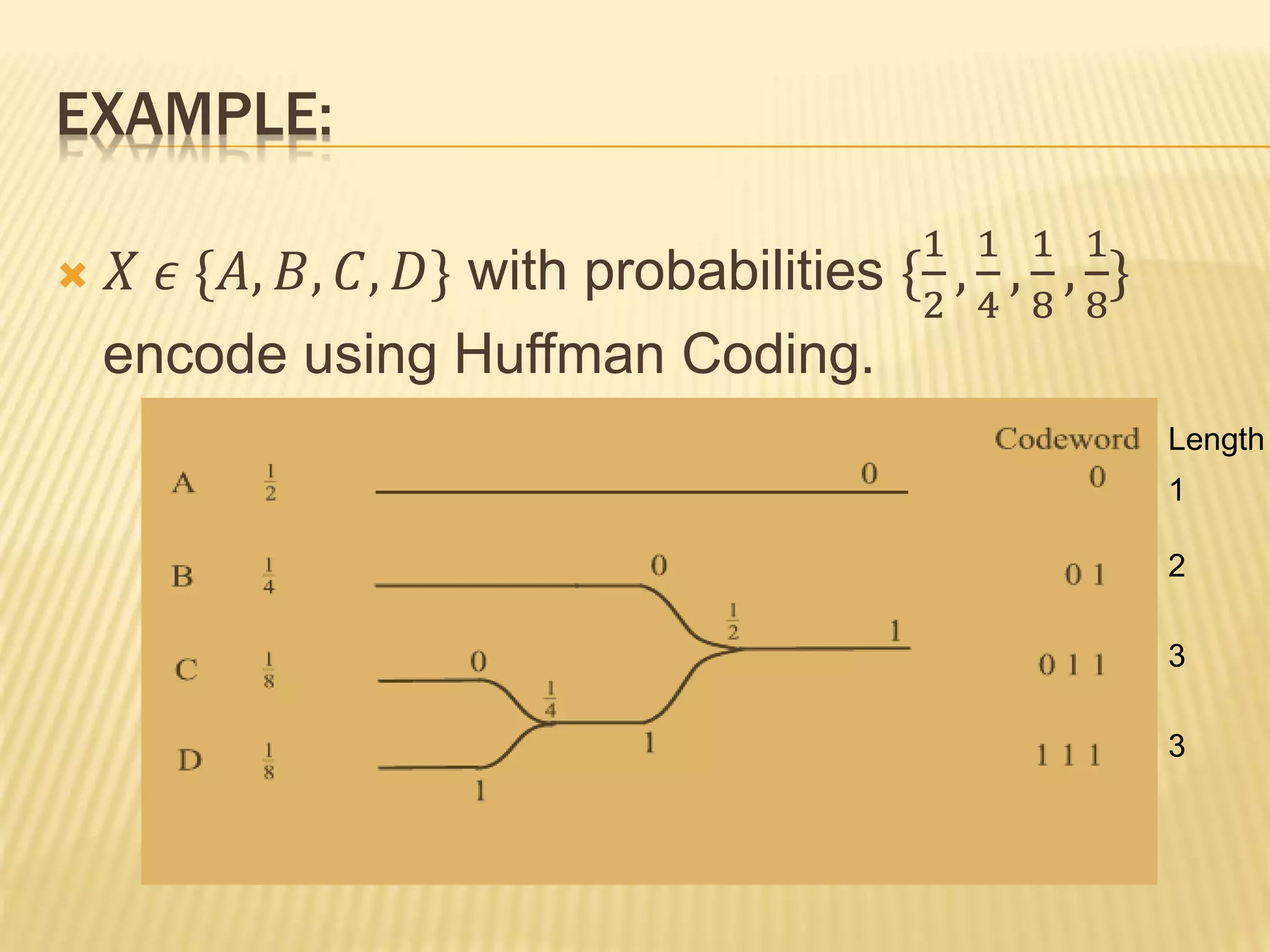
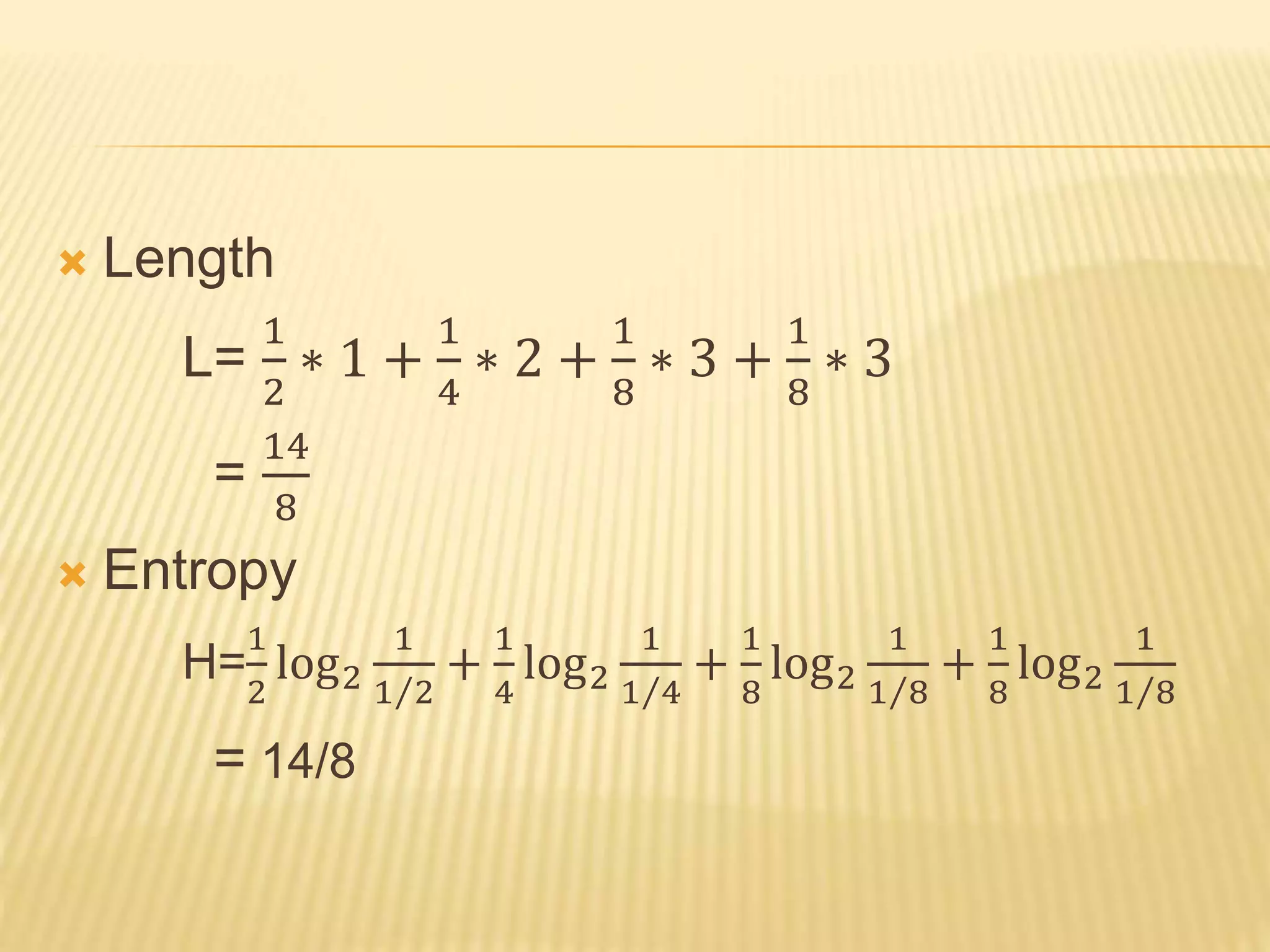
Huffman coding is a lossless data compression algorithm that assigns variable-length codes to symbols based on their frequencies. It involves arranging symbols by probability, assigning shorter codes like 0 and 1 to more probable symbols, and combining less probable symbols into a new symbol. This process repeats until only two symbols remain, which are then assigned codes moving backward. The algorithm aims to achieve maximum efficiency by keeping code lengths short for frequent symbols and long for rare symbols. An example encodes letters A-D with probabilities 1/2, 1/4, 1/8, 1/8 into codes with lengths 1, 2, 3, and 3, achieving maximum efficiency with zero redundancy.

1. HUFFMAN CODING
By: Mr. Nihal Kumar(Ass. Professor)

2. INTRODUCTION
 Huffman coding is a lossless data encoding
algorithm
 This is a method of reducing complex code
into simpler sequences and is common in
video encoding.
 This is a variable length and prefix free
coding.

3. PROCESS
 The source symbols are arranged in order of
decreasing probabilities(frequencies)
 Then the two least probabilities are assigned
to bit 0 & 1.
 Then combine last two symbols and move
the combined symbol as high as possible.
 Repeat the above step until two symbols left.
 Code for each symbol is found by moving
backward

4. CALCULATION
 Length of code
L = 𝑖=1
𝑛
𝑙𝑖 𝑃𝑖
 Entropy
H= 𝑖=1
𝑛
𝑃𝑖 log2
1
𝑃 𝑖
 Efficiency
𝜂 =
𝐻
𝐿

5.  Redundancy
𝛾 = 1 − 𝜂

6. EXAMPLE:
 𝑋 𝜖 {𝐴, 𝐵, 𝐶, 𝐷} with probabilities {
1
2
,
1
4
,
1
8
,
1
8
}
encode using Huffman Coding.
Length
1
2
3
3

7.  Length
L=
1
2
∗ 1 +
1
4
∗ 2 +
1
8
∗ 3 +
1
8
∗ 3
=
14
8
 Entropy
H=
1
2
log2
1
1 2
+
1
4
log2
1
1 4
+
1
8
log2
1
1 8
+
1
8
log2
1
1 8
= 14/8

8.  So efficiency
𝜂 =
𝐻
𝐿
=
14 8
14 8
= 1
Redundancy
𝛾 = 1 − 𝜂
= 0