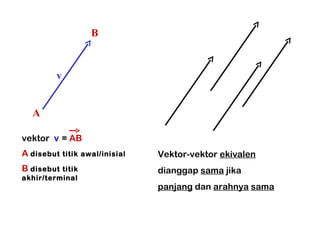
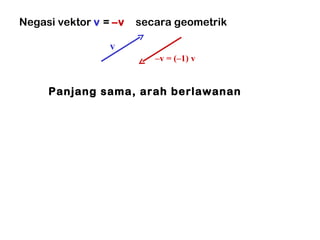
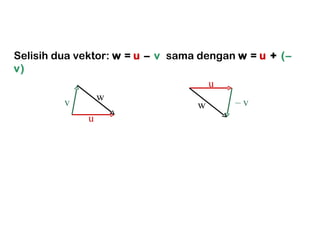
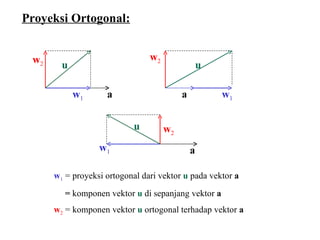
Bab ini membahas konsep vektor di ruang 2 dan 3, termasuk operasi dasar seperti penjumlahan, pengurangan, dan perkalian skalar. Juga diuraikan tentang norma vektor, perkalian titik, dan proyeksi ortogonal, serta aplikasi praktis dalam berbagai konteks. Konsep dan teorema kunci, seperti teorema aritmatika vektor dan hubungan antara vektor dikemukakan secara analitik dan grafis.

1. Chapter 3 Vectors in 2-Space and 3-Space

2. Chapter 3 3.1. Introduction to Vectors 3.2. Norm of a Vector; Vector Arithmetic 3.3. Dot Products; Projections 3.4. Cross Product 3.5. Lines and Planes in 3-Space

3. A B v vektor v = AB A disebut titik awal/inisial B disebut titik akhir/terminal Vektor-vektor ekivalen dianggap sama jika panjang dan arahnya sama

4. Negasi vektor v = –v secara geometrik v – v = (–1) v Panjang sama, arah berlawanan

5. Penjumlahan dua vektor: w = u + v secara geometrik u v w u w u u u u u u v v v v v

6. Selisih dua vektor: w = u – v sama dengan w = u + (–v) u – v w v u w

7. Penjumlahan dua vektor: w = u + v Vektor-vektor u , v , w di Ruang-2 atau Ruang-3 Ruang-2: u = (u 1 , u 2 ) ; v = (v 1 , v 2 ) ; w = (w 1 , w 2 ) w = (w 1 , w 2 ) = (u 1 , u 2 ) + (v 1 , v 2 ) = (u 1 + v 1 , u 2 + v 2 ) w 1 = u 1 + v 1 w 2 = u 2 + v 2 secara analitik:

8. Perkalian vektor dengan skalar (bilangan nyata / real number ) w = k v ; k = skalar v 3v – 2v v secara geometrik:

9. Perkalian vektor dengan skalar (bilangan nyata / real number ) w = k v ; k = skalar Cara analitik: Di Ruang-2: w = k v = ( k v 1 , k v 2 ) (w 1 , w 2 ) = ( k v 1 , k v 2 ) w 1 = k v 1 w 2 = k v 2

10. Koordinat Cartesius: P 1 = (x 1 , y 1 ) dan P 2 = (x 2 , y 2 ) P 1 dapat dianggap sebagai titik dengan koordinat (x 1 , y 1 ) atau sebagai vektor OP 1 di Ruang-2 dengan komponen pertama x 1 dan komponen kedua y 1 P 2 dapat dianggap sebagai titik dengan koordinat (x 2 , y 2 ) atau sebagai vektor OP 2 di Ruang-2 dengan komponen pertama x 2 dan komponen kedua y 2 Vektor P 1 P 2 = OP 2 – OP 1 = ( x 2 – x 1 , y 2 – y 1 )

11. Vektor-vektor di ruang-3 Aturan tangan kanan Aturan tangan-kiri x y y z z x x : 4 jari y : telapak tangan z : ibu jari Lihat Gambar 3.1.12

12. Translasi (0, 0) (k, l) sumbu-x sumbu-y sumbu-y’ sumbu-x’ (x, y) (x’, y’) P x’ = x – k y’ = y – l y l x x’ k y’ (0, 0) x = x’ + k y = y’ + l

13. Pelajari sendiri contoh “ Application to Computer Color Models” pada halaman 128 “ Global Positioning” pada halaman 133 Examples 1 – 3

14. Chapter 3 3.1. Introduction to Vectors 3.2. Norm of a Vector; Vector Arithmetic 3.3. Dot Products; Projections 3.4. Cross Product 3.5. Lines and Planes in 3-Space

15. Aritmatika vektor di Ruang-2 dan Ruang-3 Teorema 3.2.1.: u, v, w vektor-vektor di Ruang-2/Ruang-3 k, l adalah skalar (bilangan real ) u+v = v+u (u+v)+w = u+(v+w) u+0 = 0+u = u u+(-u) = (-u)+u = 0 k ( l u) = ( kl )u k (u+v) = k u + k v ( k+l )u = k u + l u 1 u = u

16. Bukti teorema 3.2.1.: Secara geometrik (digambarkan) Secara analitik (dijabarkan) Bukti secara analitik untuk teorema 3.2.1. di Ruang-3 u = (u 1 , u 2 , u 3 ); v = (v 1 , v 2 , v 3 ); w = (w 1 , w 2 , w 3 ) u + v = (u 1 , u 2 , u 3 ) + (v 1 , v 2 , v 3 ) u + 0 = (u 1 , u 2 , u 3 ) + (0, 0, 0) = (u 1 + v 1 , u 2 + v 2 , u 3 + v 3 ) = (u 1 + 0, u 2 + 0, u 3 + 0) = (v 1 + u 1 , v 2 + u 2 , v 3 + u 3 ) = (0 + u 1 , 0 + u 2 , 0 + u 3 ) = v + u = 0 + u = (u 1 , u 2 , u 3 ) = u

17. k ( l u) = k ( l u 1 , l u 2 , l u 3 ) k ( u + v ) = k ((u 1 , u 2 , u 3 ) + (v 1 , v 2 , v 3 )) = ( kl u 1 , kl u 2 , kl u 3 ) = k (u 1 + v 1 , u 2 + v 2 , u 3 + v 3 ) = kl (u 1 , u 2 , u 3 ) = ( k u 1 + k v 1 , k u 2 + k v 2 , k u 3 + k v 3 ) = kl u = ( k u 1 , k u 2 , k u 3 ) + ( k v 1 , k v 2 , k v 3 ) = k u + k v ( k + l ) u = (( k + l ) u 1 , ( k + l ) u 2 , ( k + l ) u 3 ) = ( k u 1 , k u 2 , k u 3 ) + ( l u 1 , l u 2 , l u 3 ) = k (u 1 , u 2 , u 3 ) + l (u 1 , u 2 , u 3 ) = k u + l u

18. Norma sebuah vektor: (Untuk sementara norma bisa dianggap sebagai “ panjang” vektor ) u = (u 1 , u 2 ) vektor di ruang-2 norma vektor u = || u || =  (u 1 2 + u 2 2 ) u = (u 1 , u 2 , u 3 ) vektor di ruang-3 norma vektor u = || u || =  ( u 1 2 + u 2 2 + u 3 2 ) Vektor Satuan ( unit Vector ) : suatu vektor dengan norma 1

19. Jarak antara dua titik: Ruang-2: vektor P 1 P 2 = (x 2 – x 1 , y 2 – y 1 ) jarak antara P 1 (x 1 , y 1 ) dan P 2 (x 2 , y 2 ) =  (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 Ruang-3: vektor P 1 P 2 = (x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) jarak antara P 1 (x 1 , y 1 , z 1 ) dan P 2 (x 2 , y 2 , z 2 ) =  (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 + (z 2 – z 1 ) 2 Contoh: jarak antara P 1 (2, –1, –5) dan P 2 (4, –3, 1) =  (4 – 2) 2 + (–3 + 1) 2 + (1 + 5) 2 =  44

20. Jika u adalah vektor dan k adalah skalar, maka norma k u = | k | || u ||

21. Chapter 3 3.1. Introduction to Vectors 3.2. Norm of a Vector; Vector Arithmetic 3.3. Dot Products; Projections 3.4. Cross Product 3.5. Lines and Planes in 3-Space

22. Sudut apit antara dua vektor u dan v     u u u u v v v v

23. Perkalian titik: u . v = skalar Vektor u dan v di Ruang-2 atau di Ruang-3, dengan  = sudut apit antara u dan v || u || || v || cos  jika u  0 dan v  0 u . v = 0 jika u = 0 atau v = 0 Catatan: u dan v saling tegak lurus (  = 90 o & cos  = 0)  u . v = 0 Vektor-vektor yang saling tegak lurus disebut vektor-vektor ortogonal

24. Perkalian titik: u . v = skalar Vektor u dan v di Ruang-2 atau di Ruang-3, dengan  sudut apit antara u dan v Catatan: u , v  Ruang-2  u = (u 1 , u 2 ), v = (v 1 , v 2 ) u , v  Ruang-3  u = (u 1 , u 2 , u 3 ), v = (v 1 , v 2 , v 3 ) Formula lain untuk u . v : Ruang-2: u . v = 1 u 1 v 1 + 1 u 2 v 2 Ruang-3: u . v = 1 u 1 v 1 + 1 u 2 v 2 + 1 u 3 v 3

25. Teorema 3.3.1 – 3.3.2: Vektor-vektor u , v , w di Ruang-2 atau di Ruang-3; k adalah skalar v.v = || v || 2 , atau || v || = ( v.v ) 1/2 jika u  0 , v  0 dan mengapit sudut  , maka  lancip  u .v  0  tumpul  u .v  0  = 90 o  u .v = 0 u . v = v . u u . (v + w) = u .v + u .w k (u . v) = ( k u) . v = u . ( k v) v .v  0 jika v  0 dan v . v = 0 jika v = 0

26. Teorema 3.3.1 – 3.3.2: Vektor-vektor u , v , w di Ruang-2 atau di Ruang-3; k adalah skalar Buktikan : v . v = || v || 2 , atau || v || = ( v.v ) 1/2 Bukti: v . v = ||v|| ||v|| cos 0 o v . v = v 1 v 1 + v 2 v 2 = || v || || v || (1) = || v || 2 = v 1 2 + v 2 2 = || v || 2 = || v || 2 Buktikan : u . v = v . u Bukti : u . v = ||u|| ||v|| cos  = ||v|| ||u|| cos  = v . u

27. Teorema 3.3.1 – 3.3.2: Vektor-vektor u , v , w di Ruang-2 atau di Ruang-3; k adalah skalar Buktikan : u . (v + w) = u .v + u .w Bukti: u . (v + w) = (u 1 , u 2 , u 3 ) . ( v 1 +w 1 , v 2 +w 2 , v 3 +w 3 ) = u 1 ( v 1 +w 1 ) + u 2 ( v 2 +w 2 ) + u 3 ( v 3 +w 3 ) = (u 1 v 1 +u 1 w 1 ) + (u 2 v 2 +u 2 w 2 ) + (u 3 v 3 +u 3 w 3 ) = (u 1 v 1 +u 2 v 2 + u 3 v 3 ) + (u 1 w 1 + u 2 w 2 +u 3 w 3 ) = u .v + u .w Buktikan : k (u . v) = ( k u) . v = u . ( k v) Bukti: k (u . v) = k (u 1 v 1 + u 2 v 2 + u 3 v 3 ) …………. = ( k u 1 v 1 + k u 2 v 2 + k u 3 v 3 ) = (u 1 k v 1 + u 2 k v 2 + u 3 k v 3 ) = ( k u 1 )v 1 + ( k u 2 )v 2 + ( k u 3 )v 3 = u 1 ( k v 1 ) + u 2 ( k v 2 ) + u 3 ( k v 3 ) = ( k u) . v = u . ( k v)

28. Teorema 3.3.1 – 3.3.2: Vektor-vektor u , v , w di Ruang-2 atau di Ruang-3; k adalah skalar Buktikan : jika v  0 maka v . v  0 Bukti : v = ( v 1 , v 2 ) sehingga v . v = v 1 v 1 + v 2 v 2  0 karena kwadrat suatu bilangan selalu positif Buktikan : jika v = 0 (vektor) maka v . v = 0 (skalar) Bukti : v = ( 0, 0 ) sehingga v . v = 0 + 0 = 0

29. Proyeksi Ortogonal: w 1 = proyeksi ortogonal dari vektor u pada vektor a = komponen vektor u di sepanjang vektor a w 2 = komponen vektor u ortogonal terhadap vektor a u a w 1 w 2 u u a a w 1 w 1 w 2 w 2

30. Proyeksi Ortogonal: w 1 = proyeksi ortogonal dari vektor u pada vektor a = komponen vektor u di sepanjang vektor a w 2 = komponen vektor u ortogonal terhadap vektor a u a w 1 w 2 u u a a w 1 w 1 w 2 w 2

31. Proyeksi Ortogonal: u w 1 w 2 a w 1 = proyeksi ortogonal dari vektor u pada vektor a w 2 = komponen vektor u ortogonal terhadap vektor a w 1 = ( u . a / || a || 2 ) a w 2 = u – ( u . a / || a || 2 ) a Bukti: w 1 = ( k ) a  k = ( u . a / || a || 2 ) ? u = w 1 + w 2 = k a + w 2 u . a = ( k a + w 2 ) . a = k a . a + w 2 . a = k || a || 2 + 0 = k || a || 2 k = ( u . a ) / || a || 2 Norm vektor w 1 = || w 1 || = | u . a | || a || / || a || 2 = | u . a | / || a ||

32. Jarak titik P o (x o , y o ) ke garis lurus g : ax +by +c = 0 | ax o + by o + c|  (a 2 + b 2 )

33. Jarak titik P o (x o , y o ) ke garis lurus g : ax +by +c+= 0 g : ax + by + c = 0 n Q (x 1 , y 1 ) Vektor n = (a, b) ortogonal garis g Bukti bahwa n = (a, b) ortogonal garis g R(x 2 , y 2 ) * * Vektor QR = (x 2 – x 1 , y 2 – y 1 ) Dengan perkalian titik: n . QR = a(x 2 – x 1 ) + b (y 2 – y 1 ) R terletak pada garis g, maka: ax 2 + by 2 + c = 0 Q terletak pada garis g, maka: ax 1 + by 1 + c = 0 a(x 2 – x 1 ) + b (y 2 – y 1 ) + 0 = 0 Jadi, n . QR = a(x 2 – x 1 ) + b (y 2 – y 1 ) = 0 artinya vektor n ortogonal QR, sehingga vektor n ortogonal garis g (terbukti)

34. Jarak titik P o (x o , y o ) ke garis lurus g : ax +by +c+= 0 g : ax + by + c = 0 n o P o (x o , y o ) Q (x 1 , y 1 ) Vektor QP o = (x o – x 1 , y o – y 1 ) ( vektor QP o seperti vektor u ; vektor n seperti vektor a vektor d seperti vektor w 1 ) jarak dari titik P o ke garis g = || d || d || w 1 || = | u . a | / || a || || d || = | QP o . n | / || n || = |(x o – x 1 , y o – y 1 ) . (a, b)| /  (a 2 + b 2 ) = | (x o – x 1 )a +(y o – y 1 )b) | /  (a 2 + b 2 ) = | x o a – x 1 a + y o b – y 1 b | /  (a 2 + b 2 ) tetapi Q terletak di g, maka ax 1 + by 1 + c = 0 atau c = – ax 1 – by 1 Maka || d || = | ax o + by o – ax 1 – by 1 | /  (a 2 + b 2 ) = | ax o + by o + c| /  (a 2 + b 2 )

35. Pekerjaan Rumah untuk tgl 28-10-2011 (dipresentasikan) 3.1. no. 5, 11 3.2. no. 3, 9 3.3. no. 8, 27