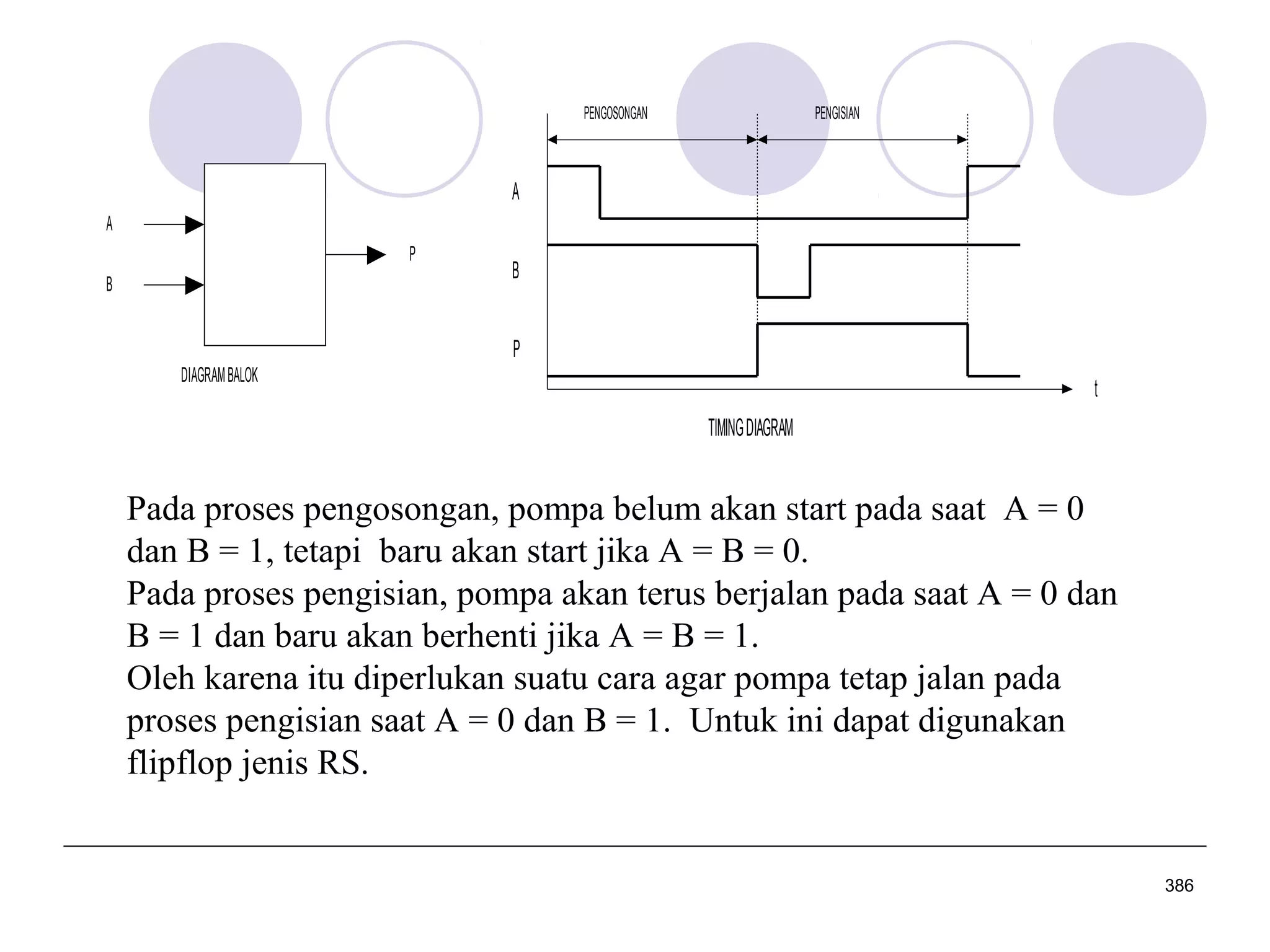
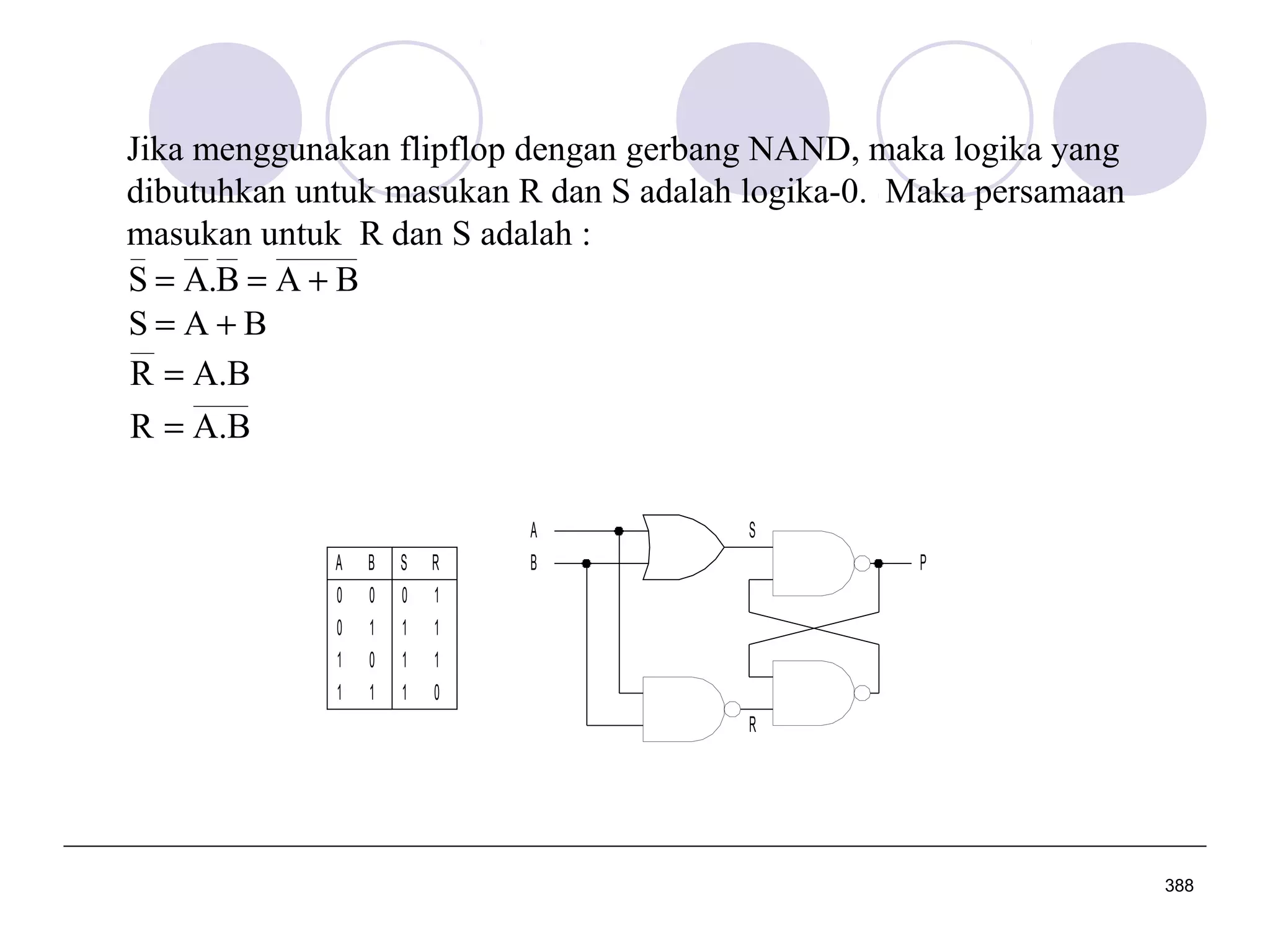
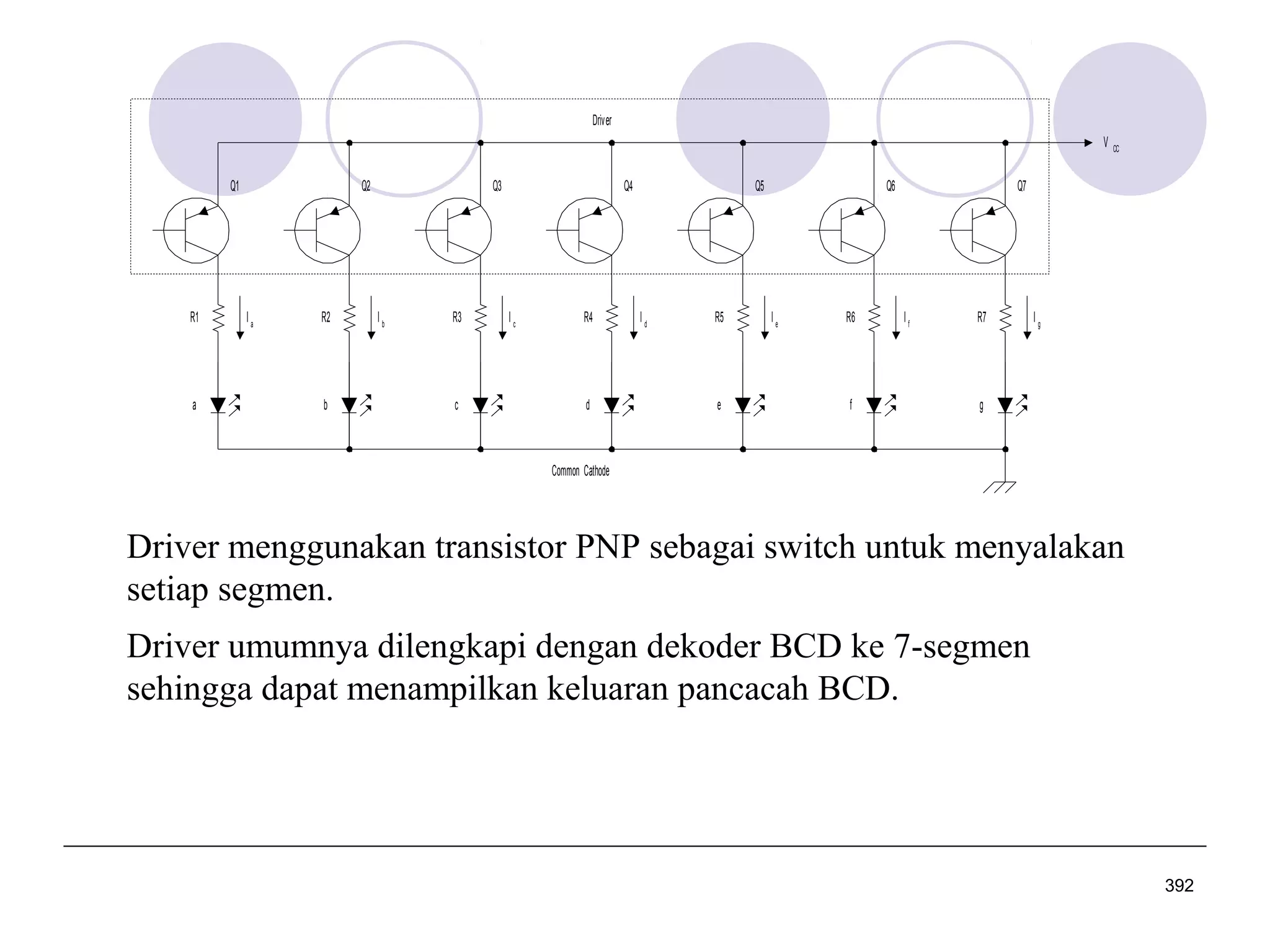
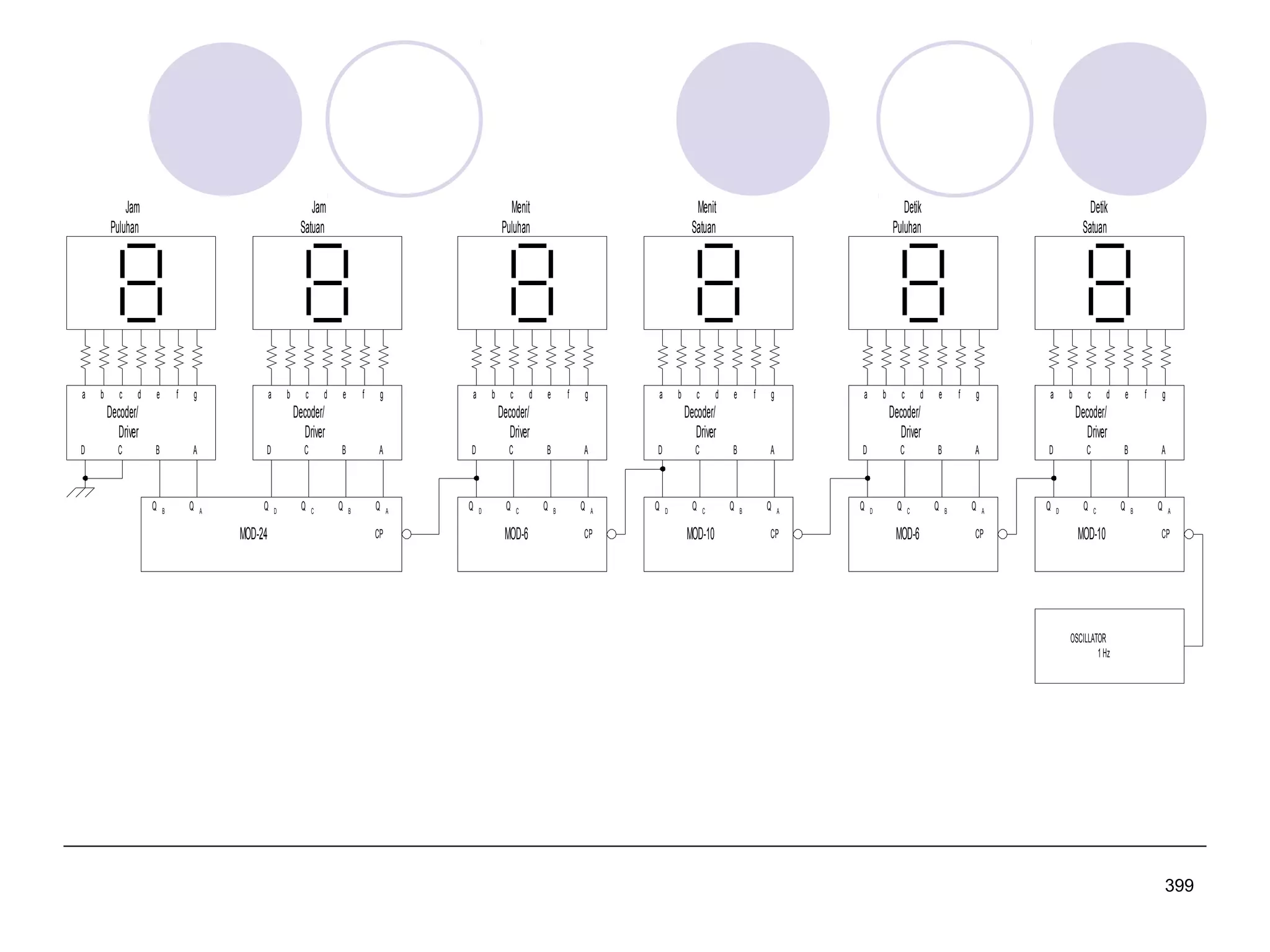
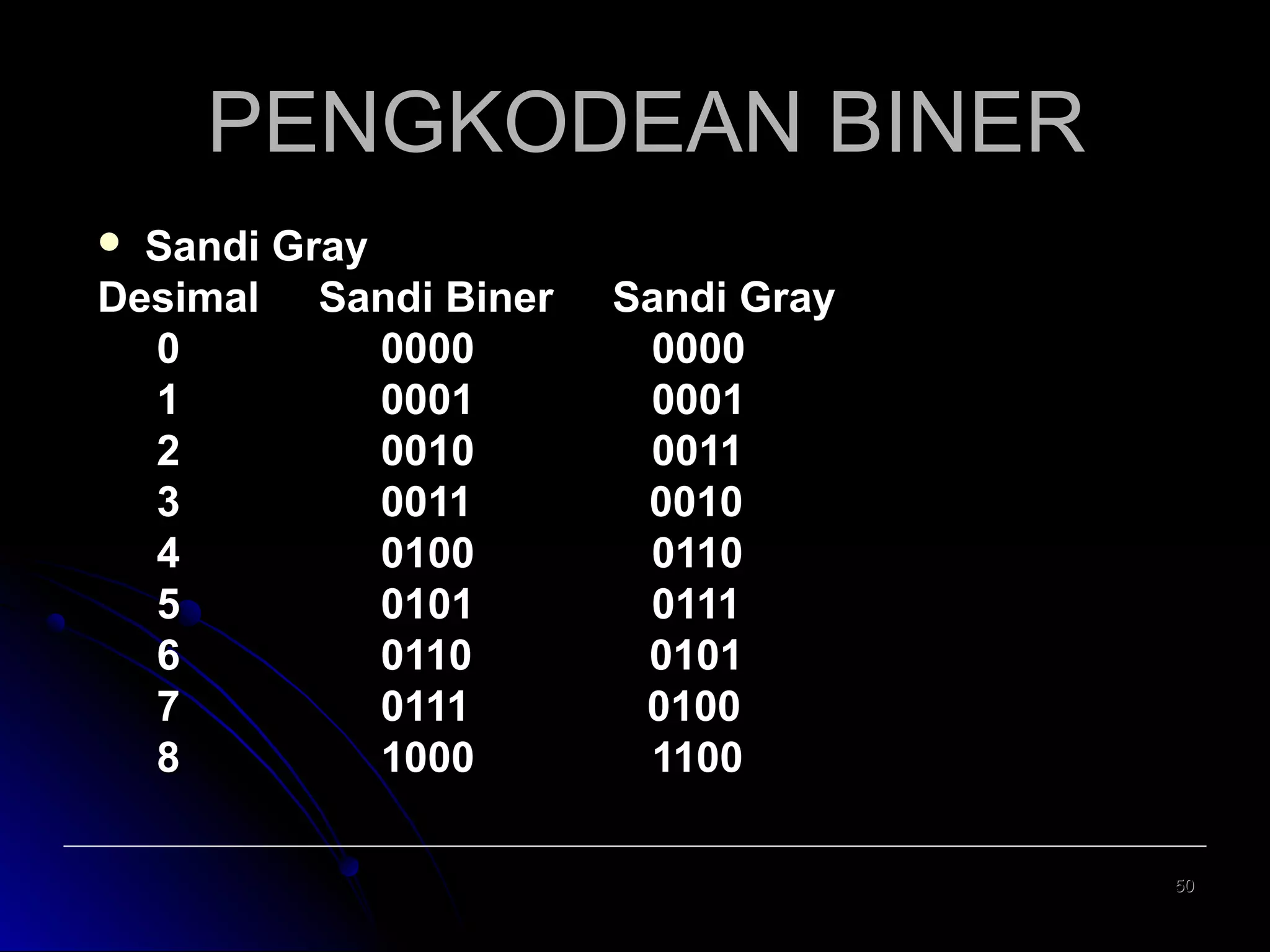
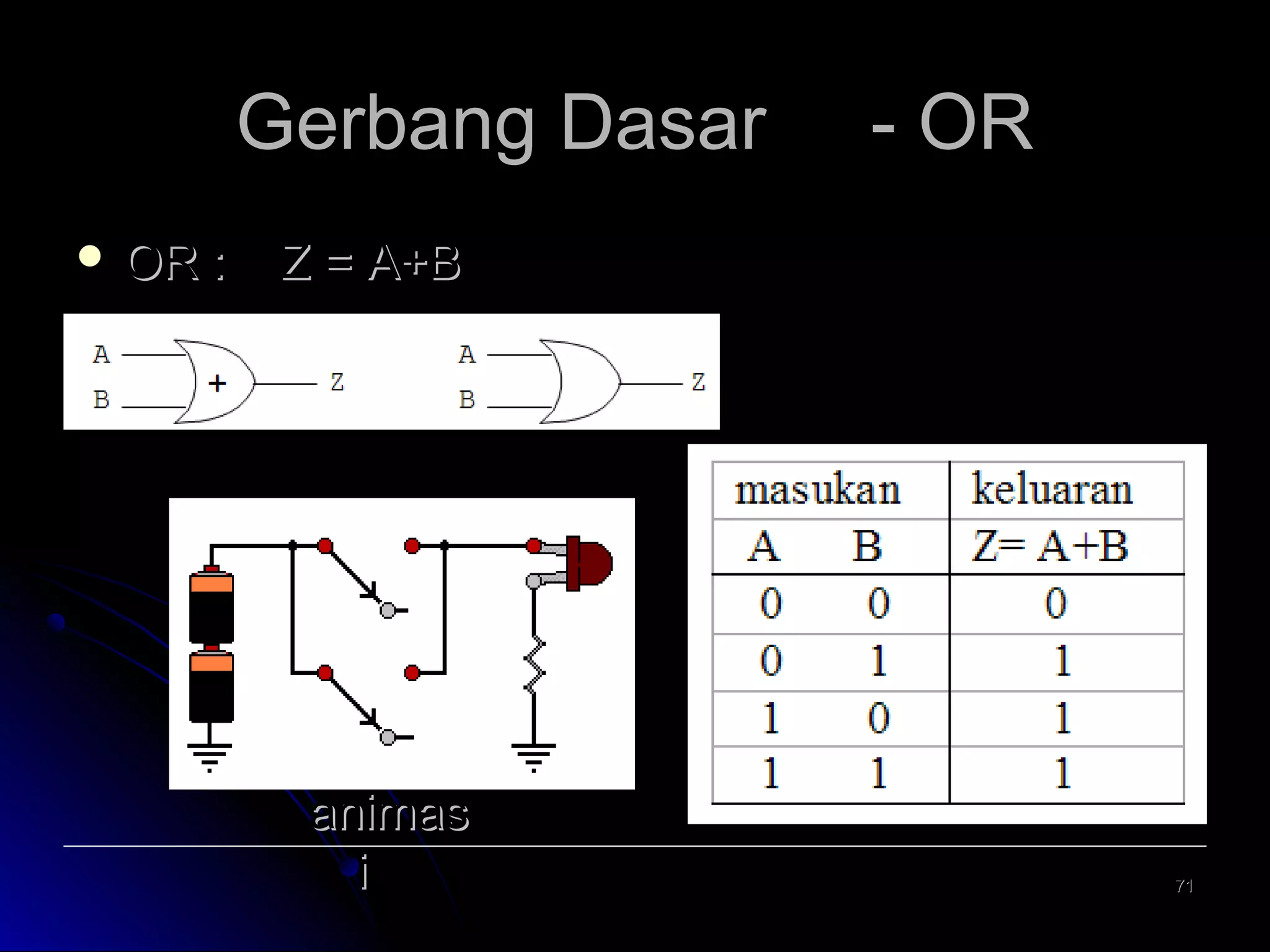
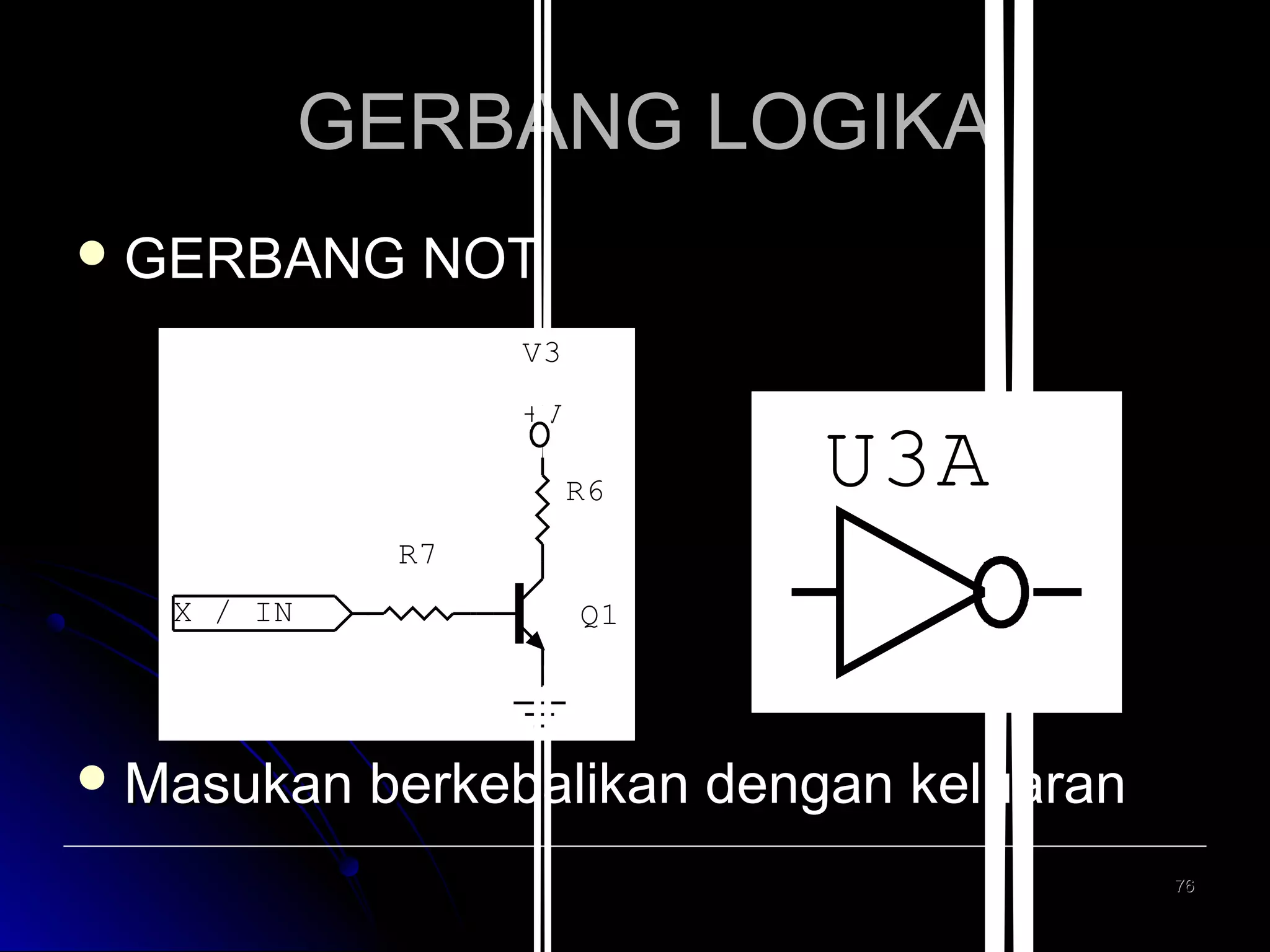
Dokumen ini adalah kuliah dasar tentang sistem digital yang mencakup perancangan logika digital, sistem bilangan, dan pengkodean biner. Ini memberikan penjelasan mengenai berbagai jenis sistem bilangan, konversi antara sistem, dan penggunaan komplemen dalam perhitungan aritmatika digital. Mata kuliah ini penting untuk program studi teknik elektro dan terkait dengan berbagai mata kuliah lanjutan di bidang teknik elektronika dan telekomunikasi.














![Biner, Oktal, Hexadesimal [2]
Biner
: 101,01 =
(5,25)
2
10
Oktal
:
Hexadesimal :
18](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-18-2048.jpg)

![Konversi [2]
Biner
– Oktal
bilangan biner dikelompokkan atas 3 bit
1 011 001 111 = (1) (3) (1) (7) 8
Biner
– Hexadesimal
bilangan biner dikelompokkan atas 4 bit
10 1100 1111 = (2) (C) (F)
16
20](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-20-2048.jpg)











































































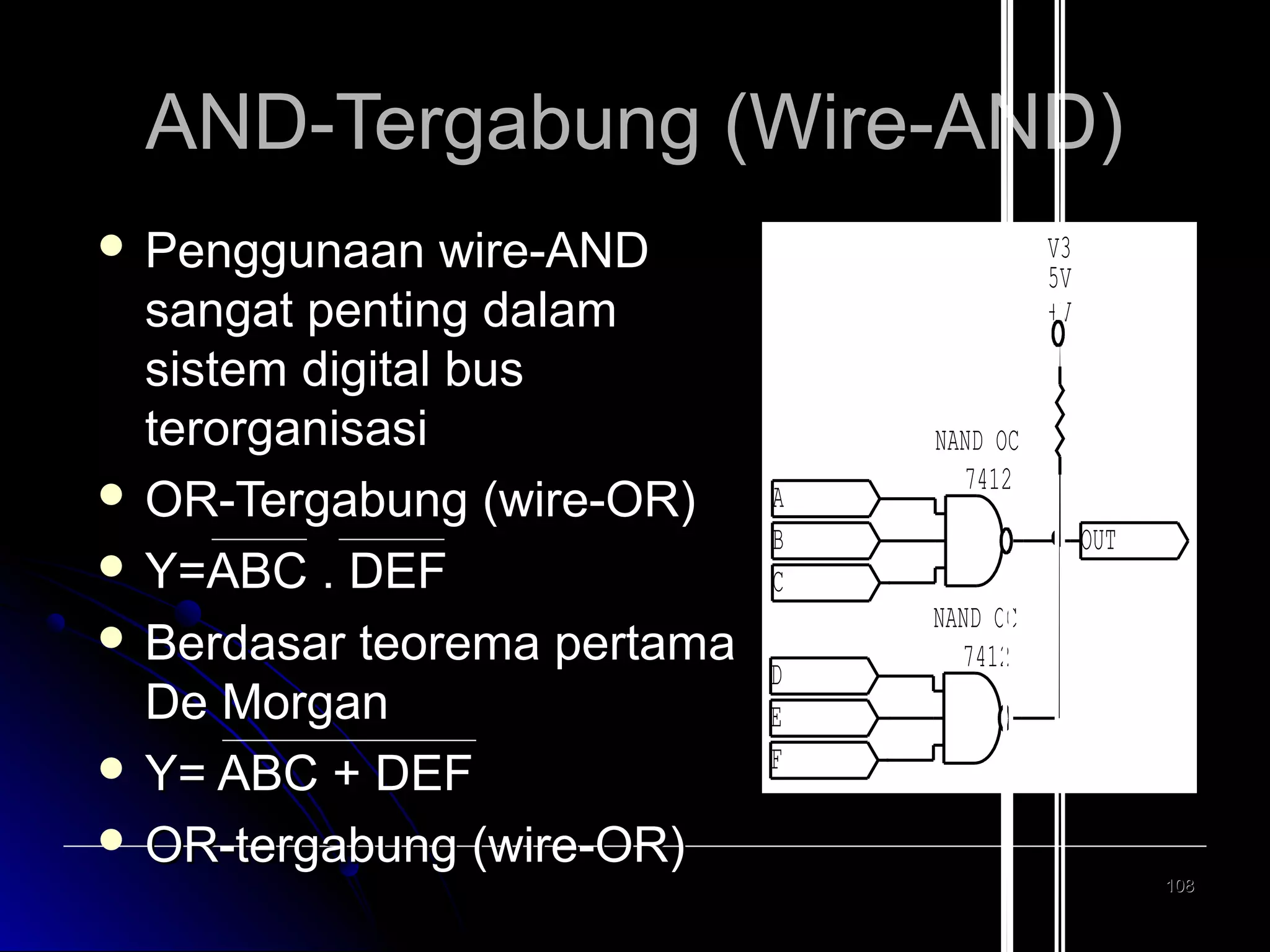















































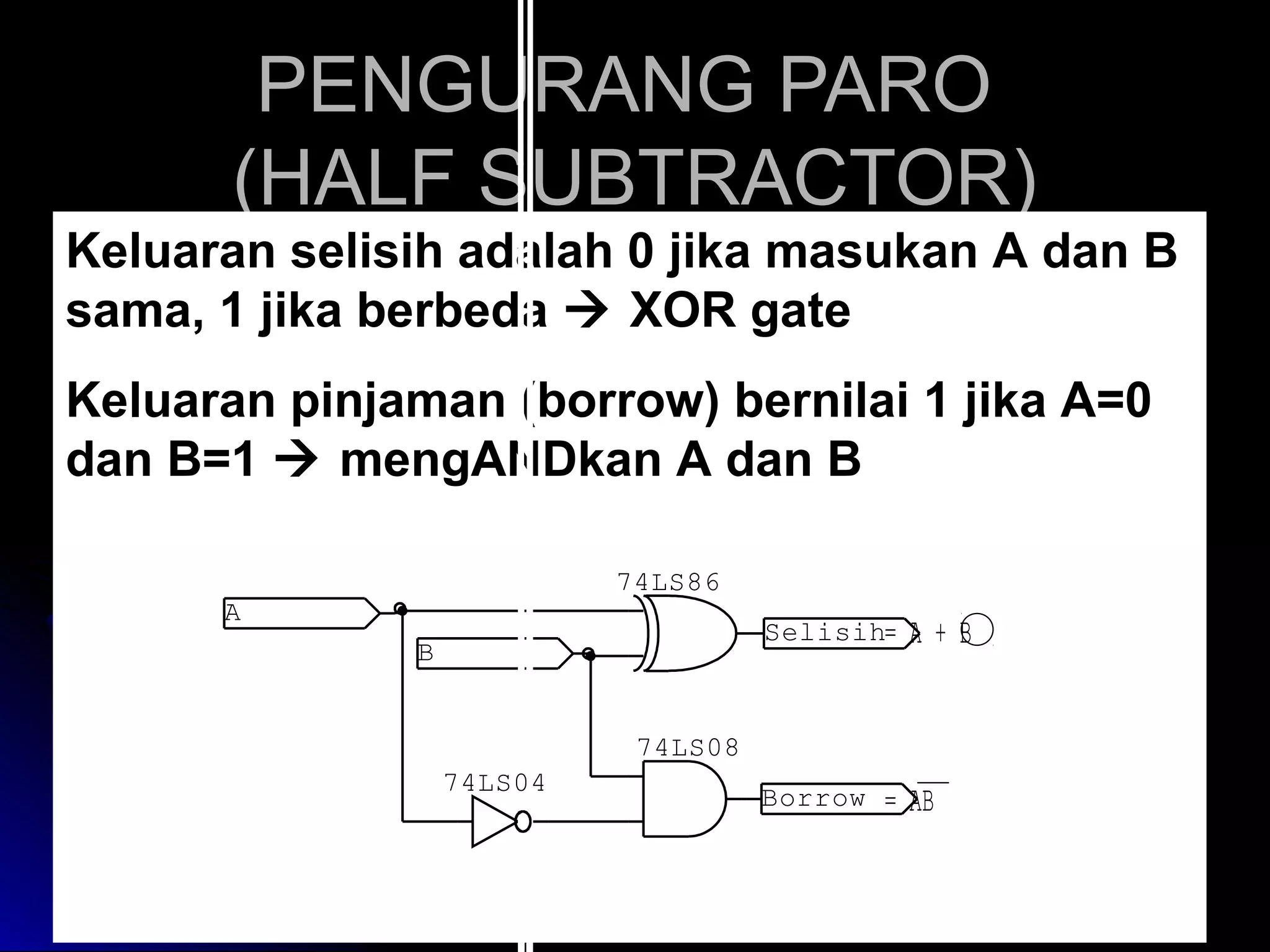









































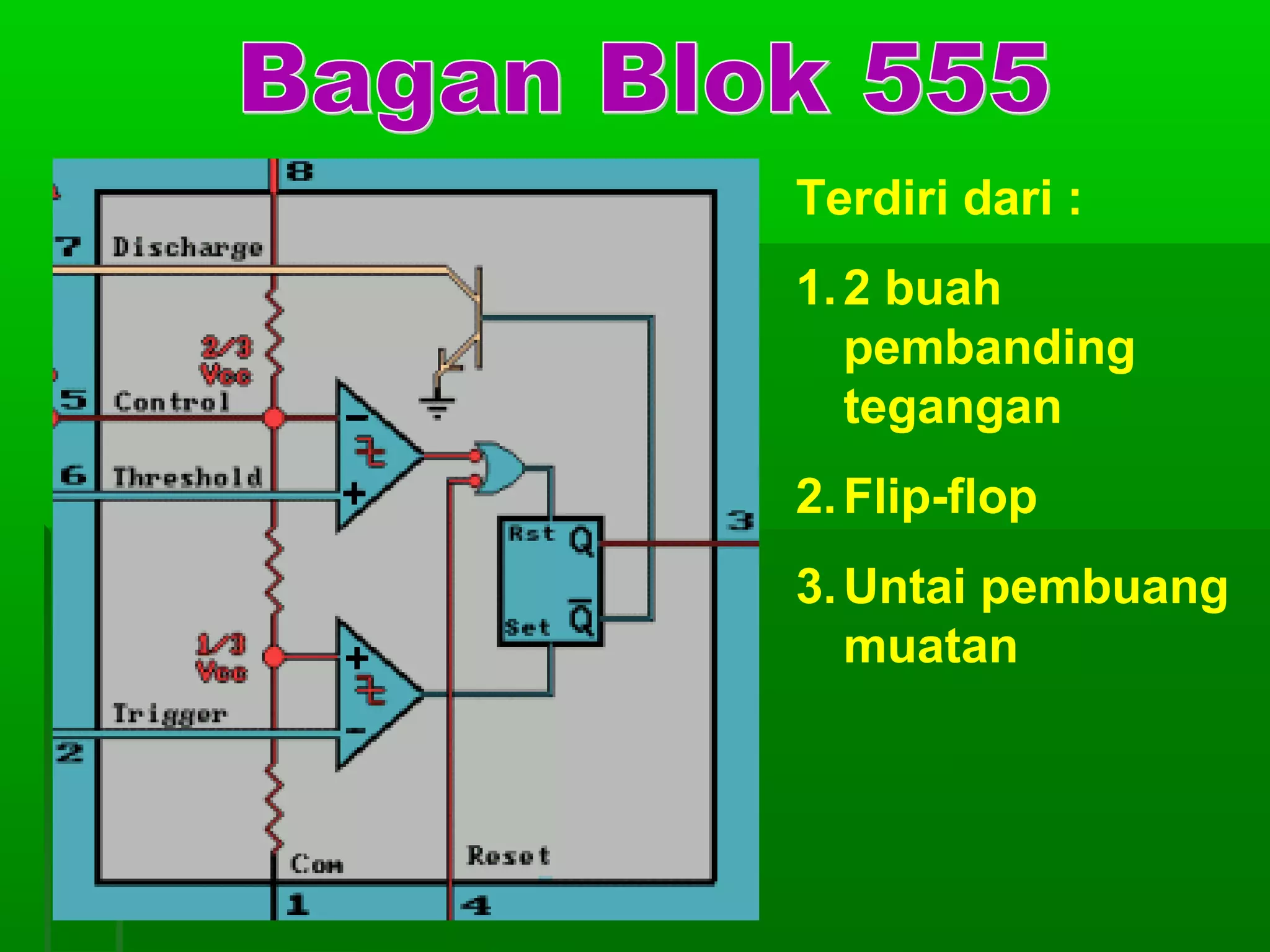
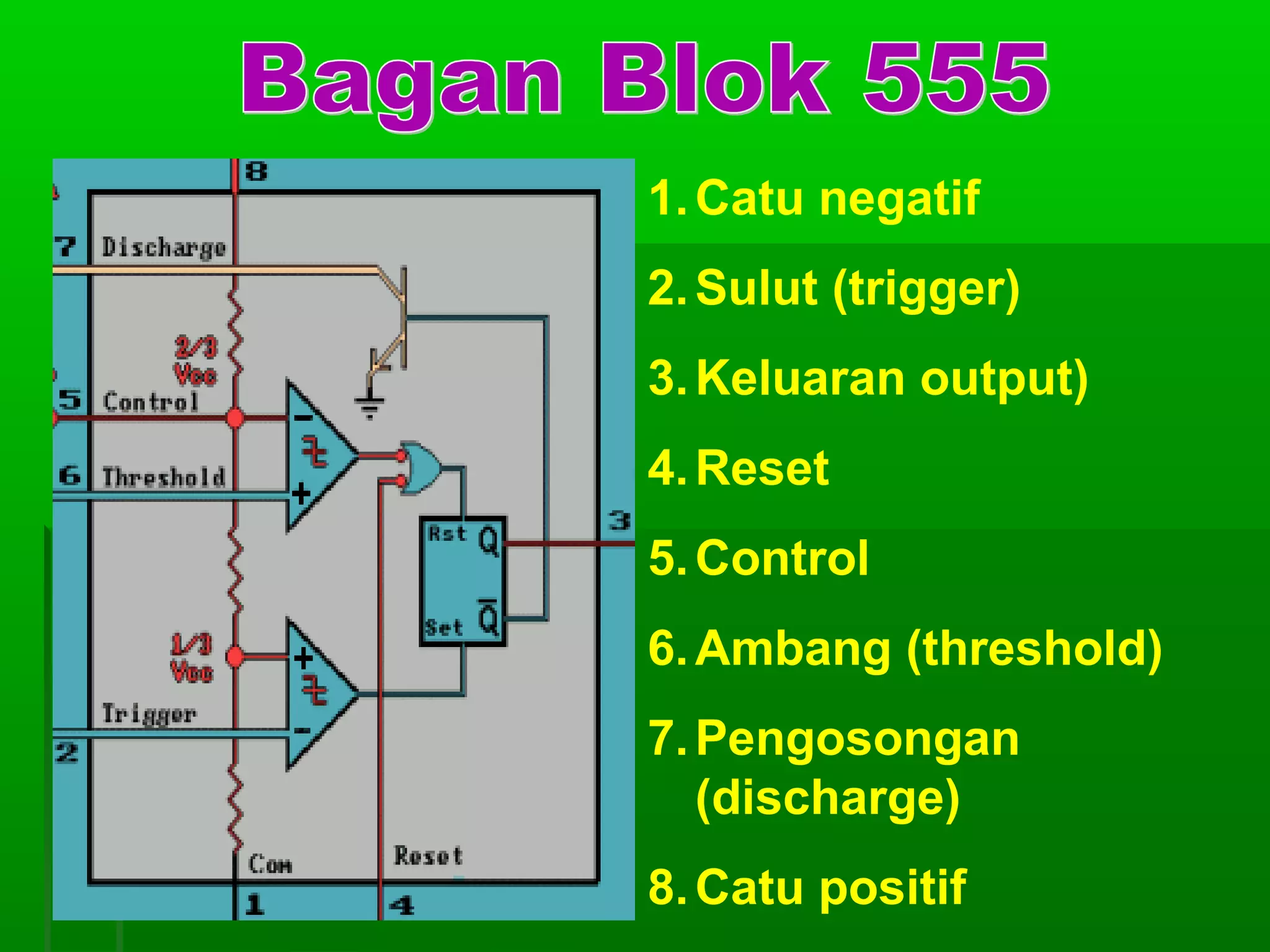














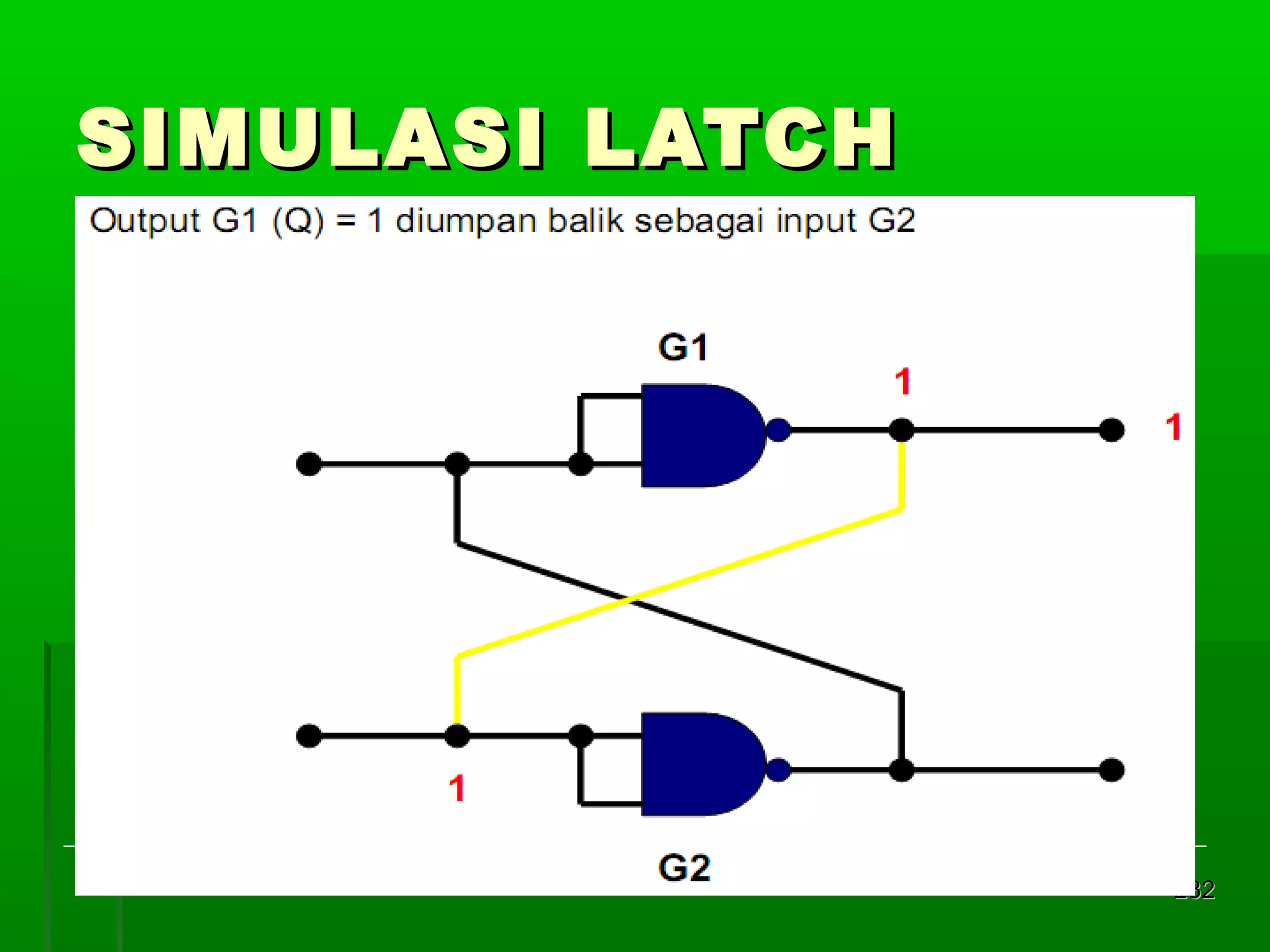
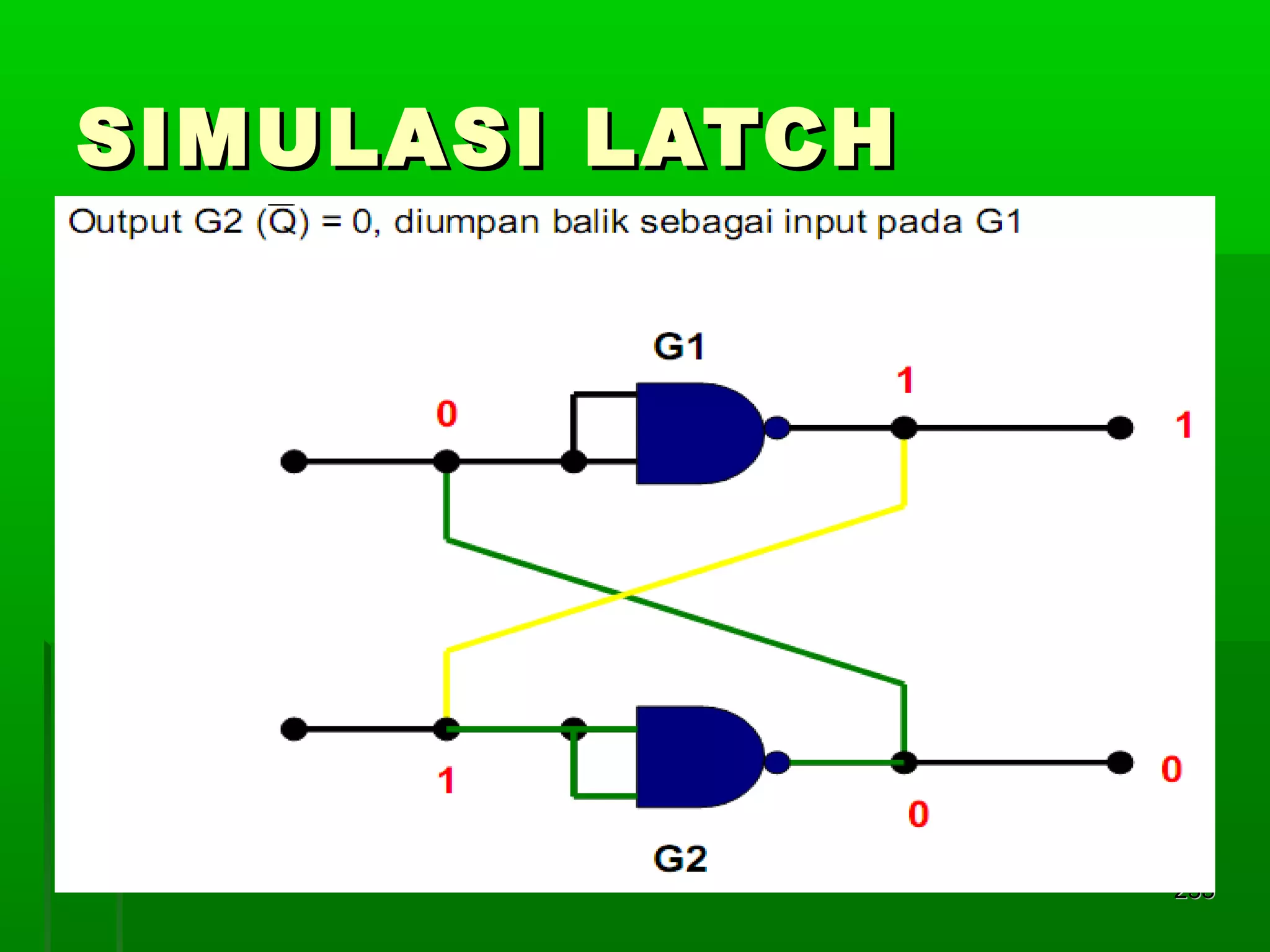

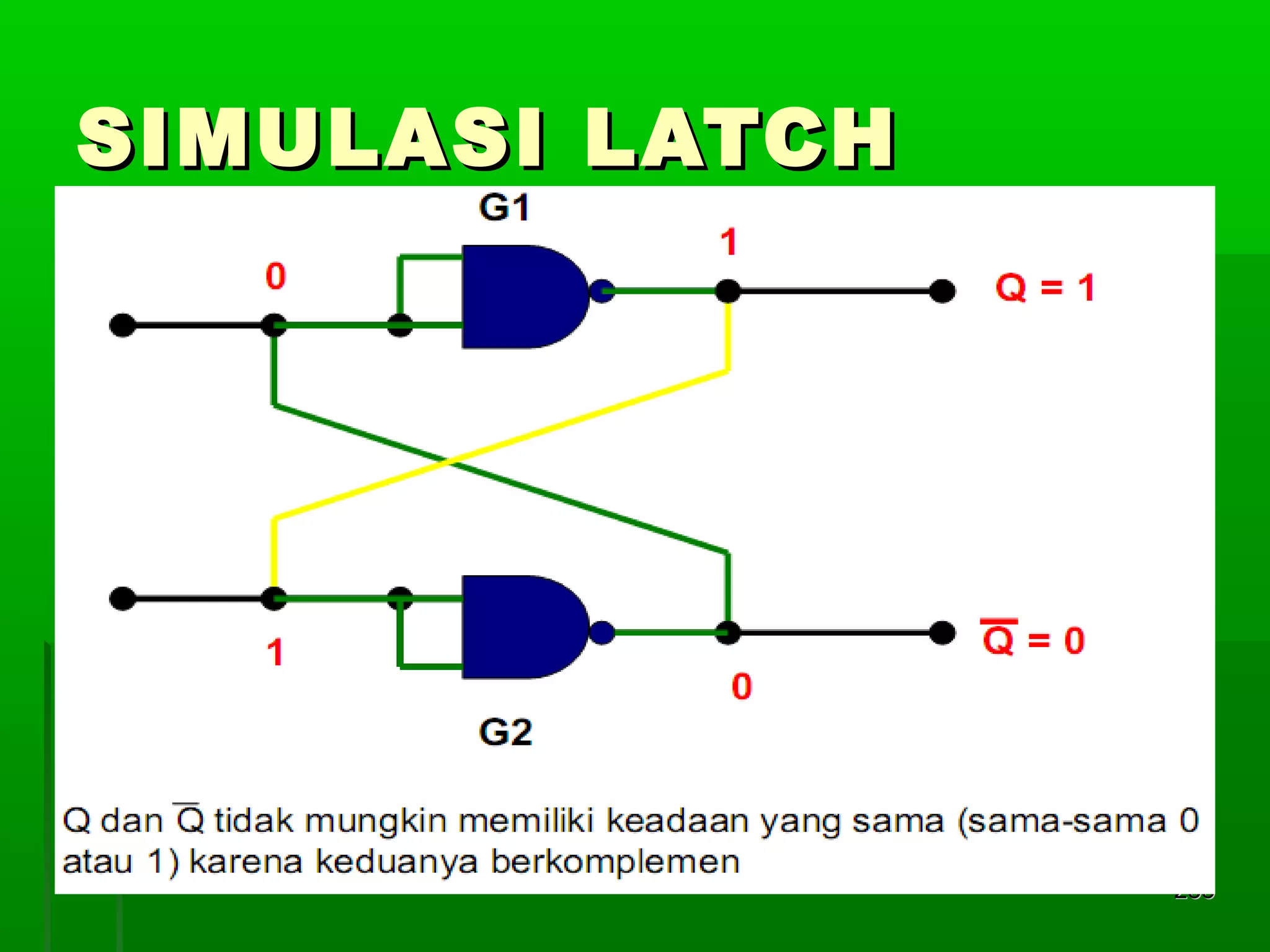


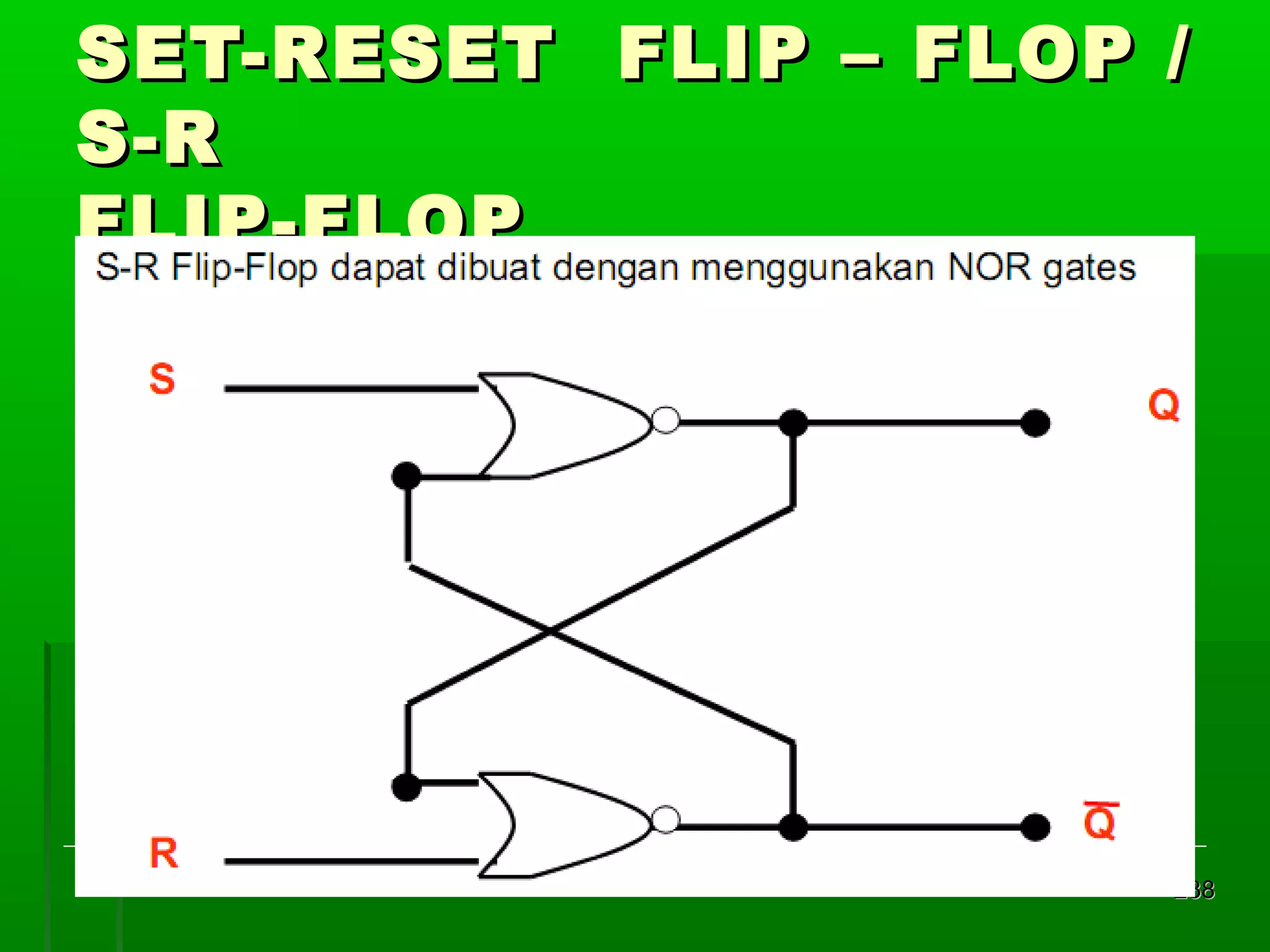

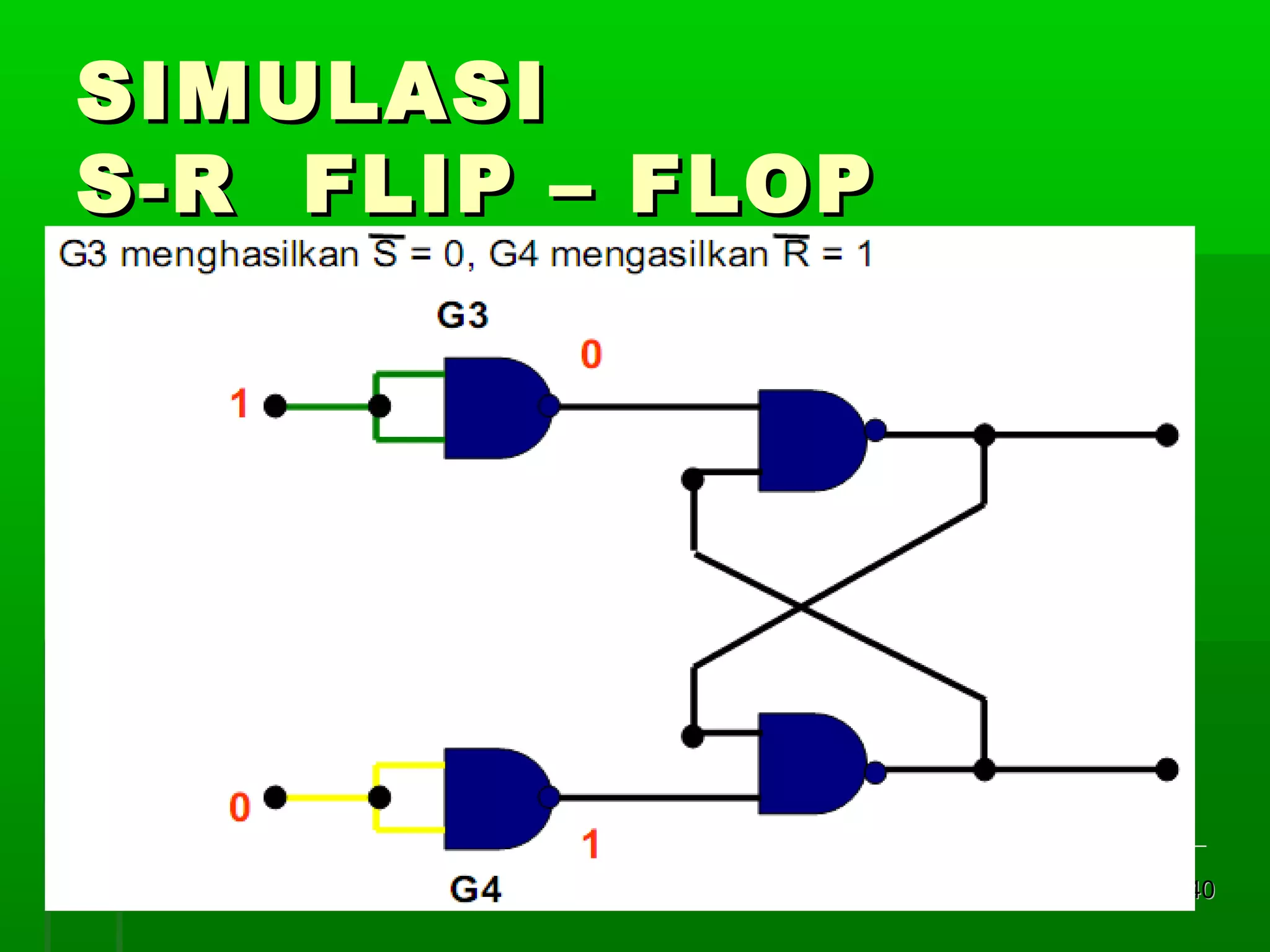
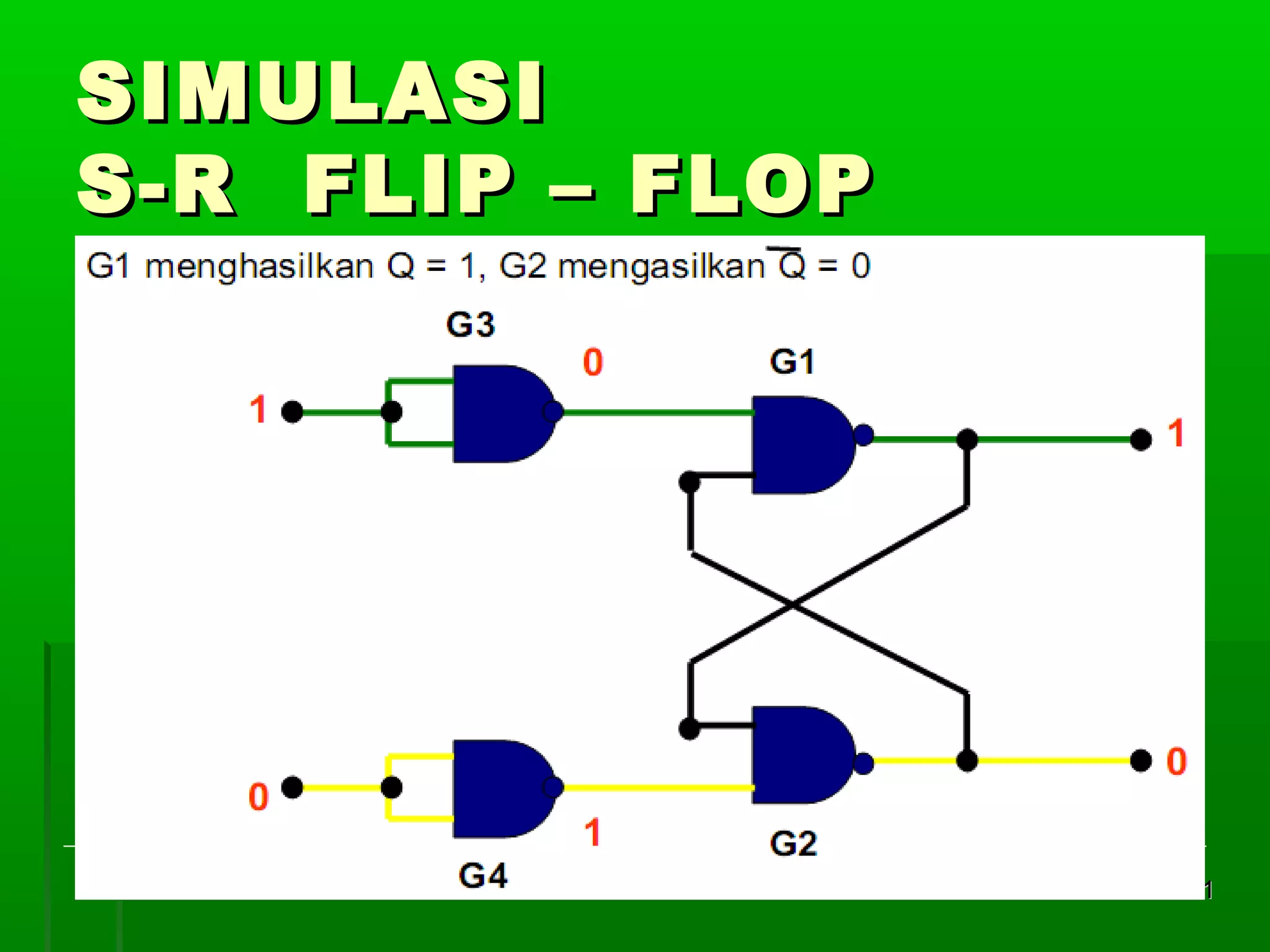
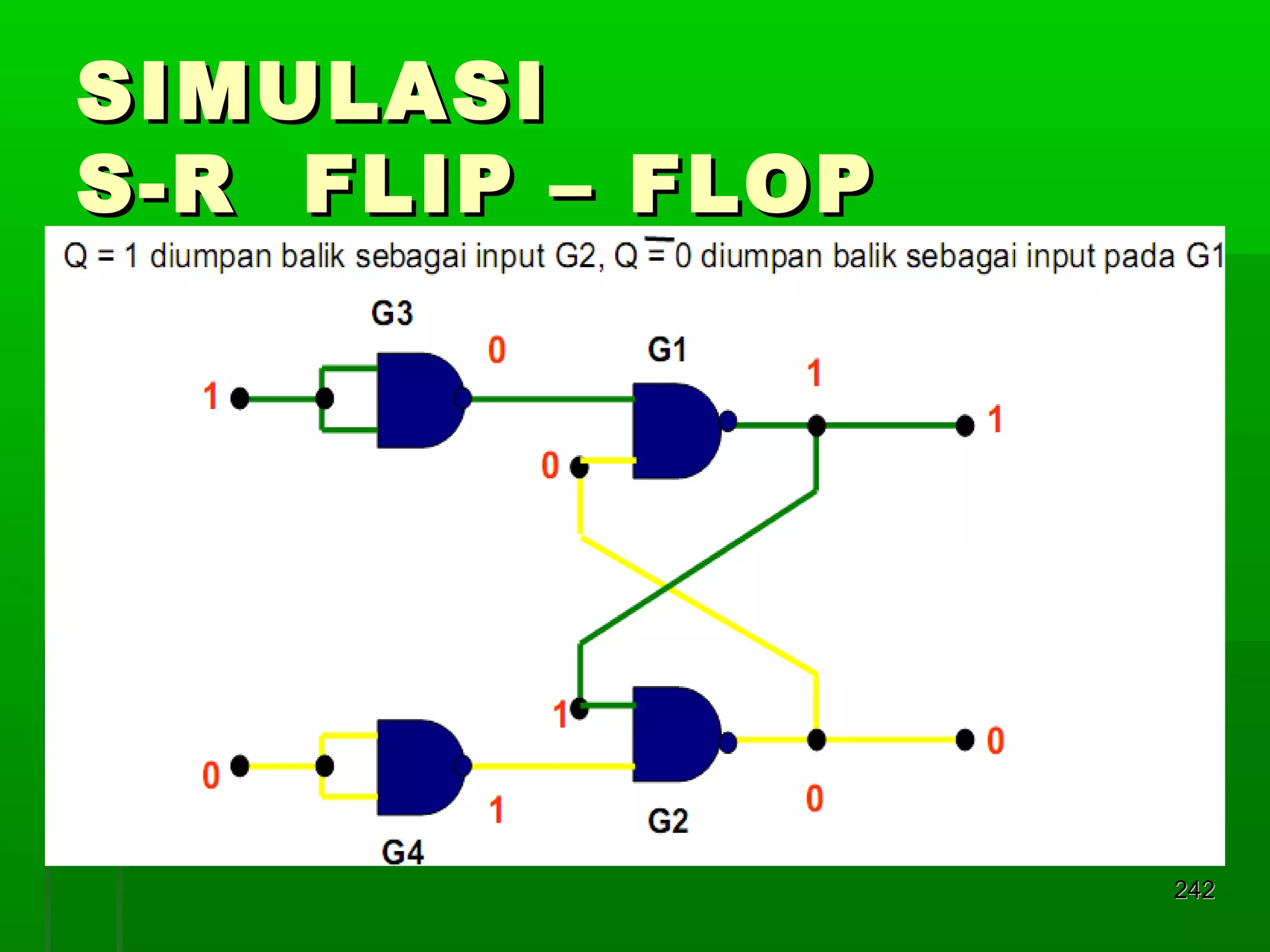
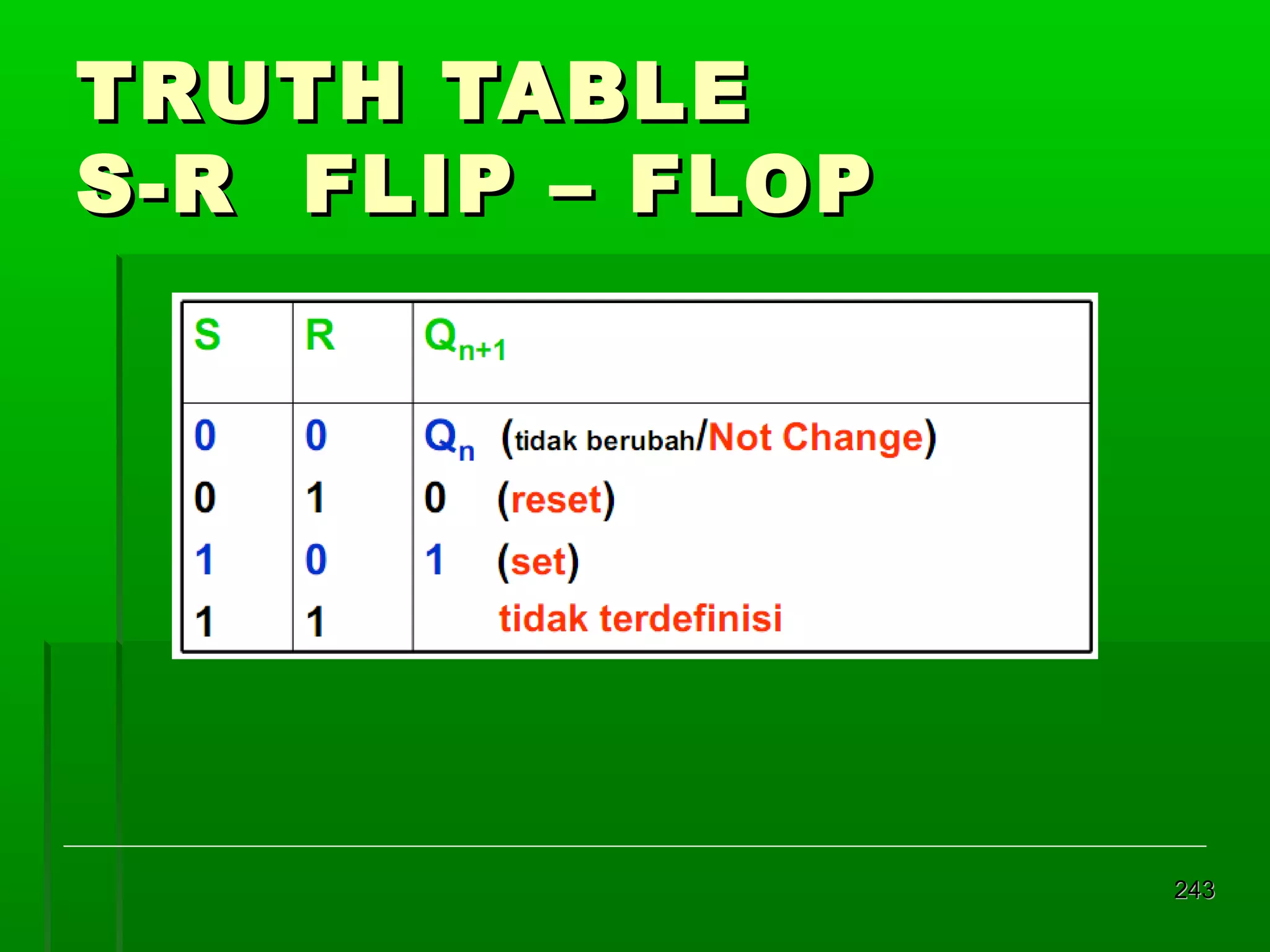

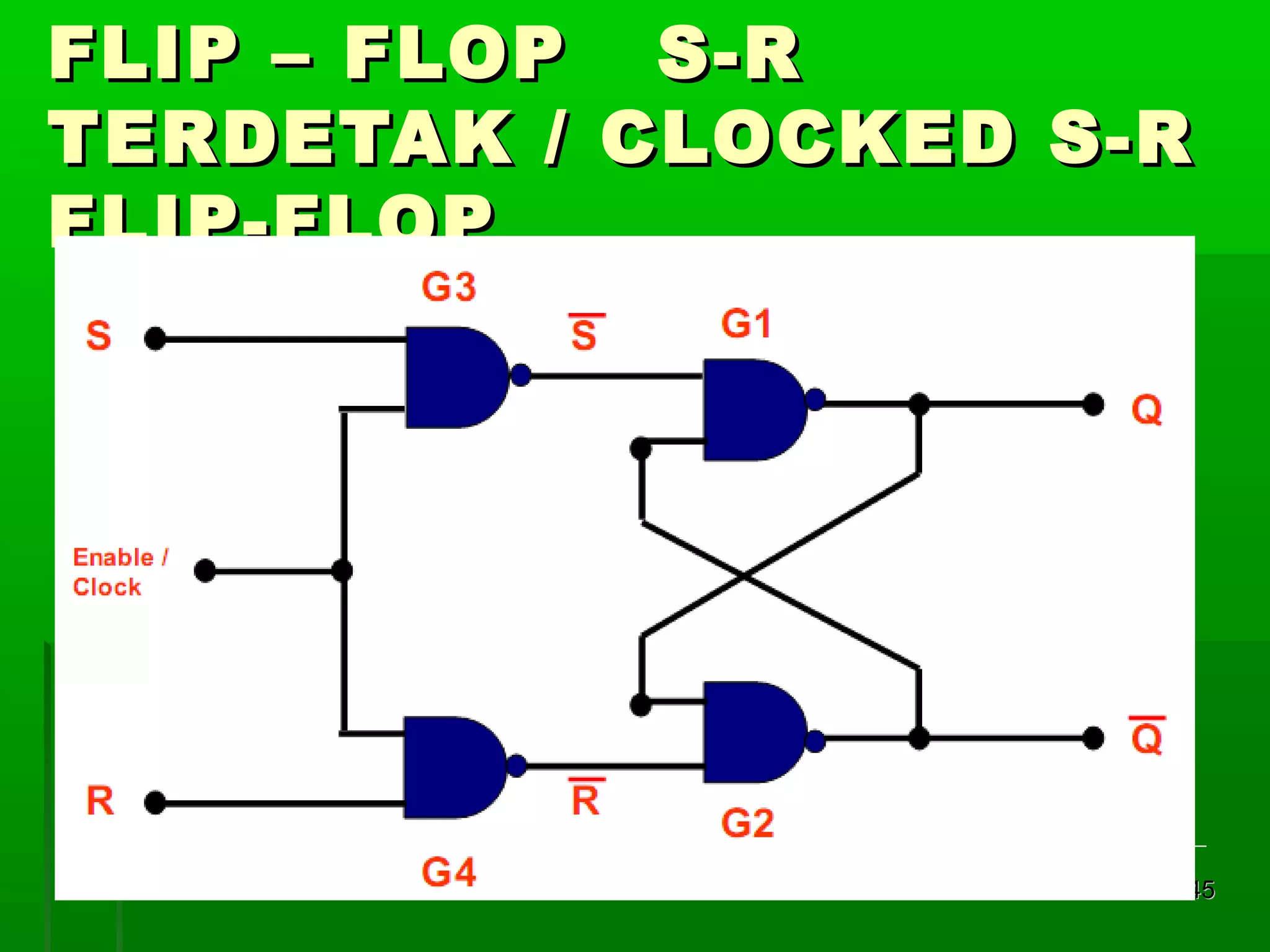






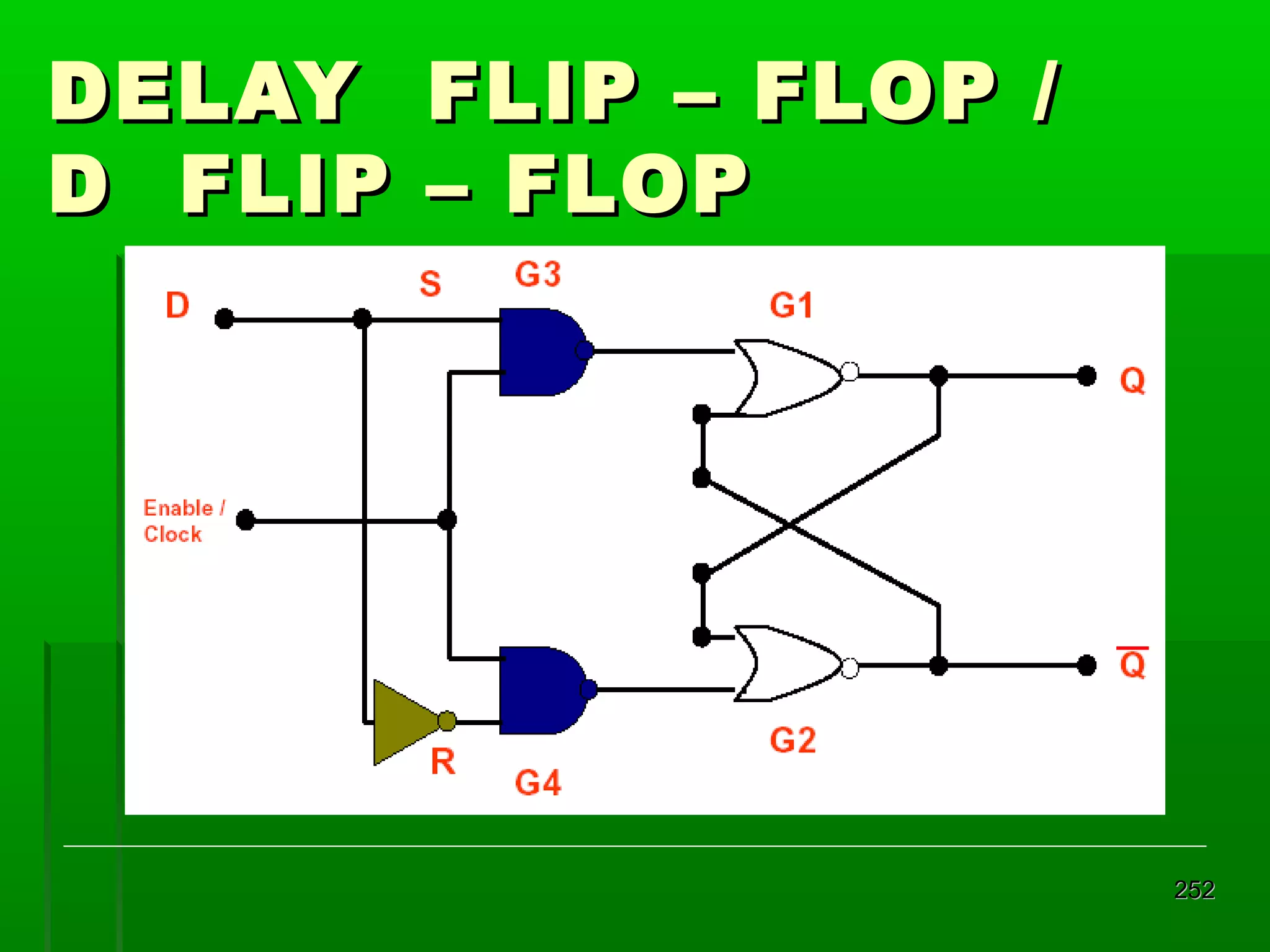


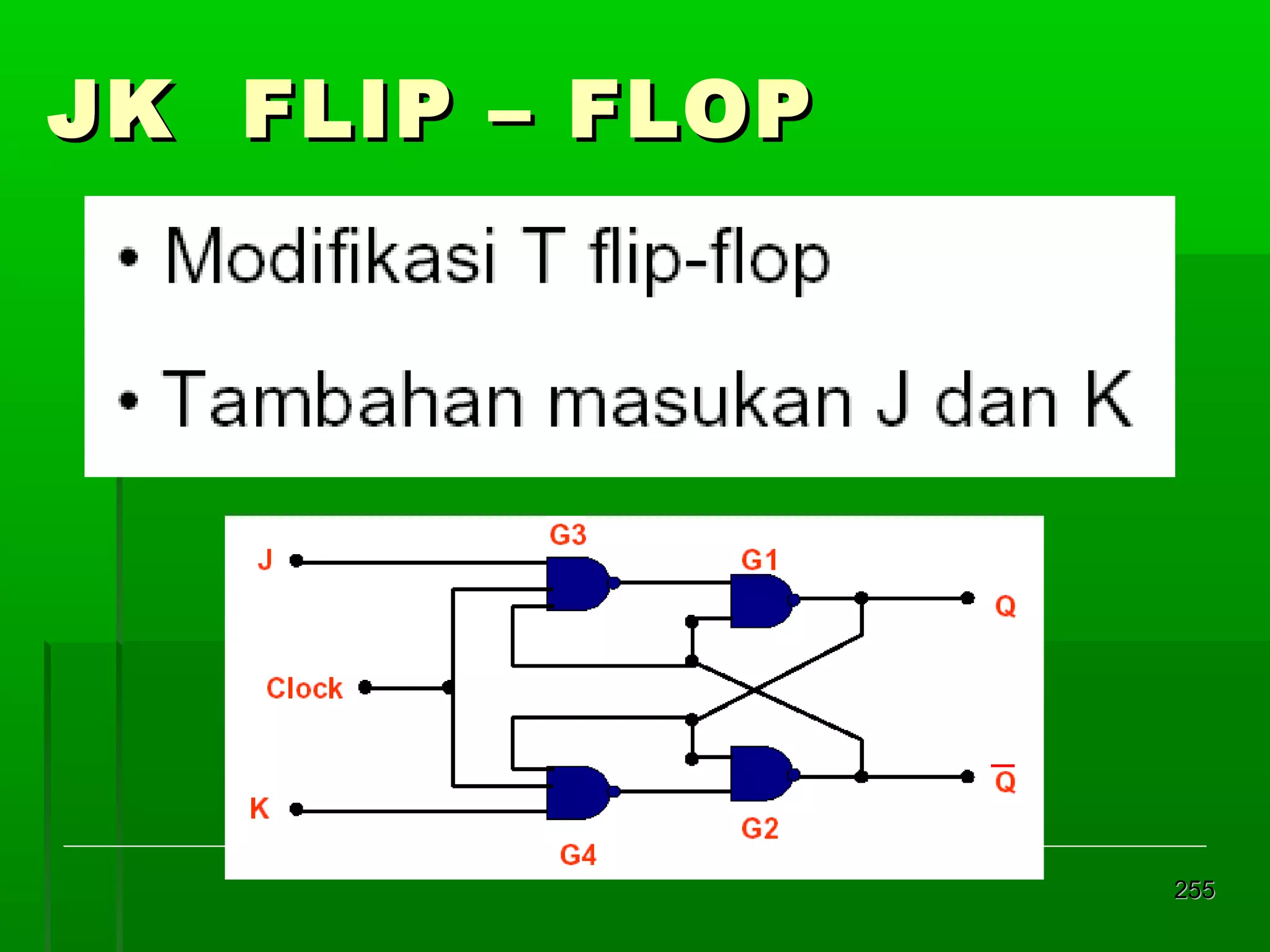

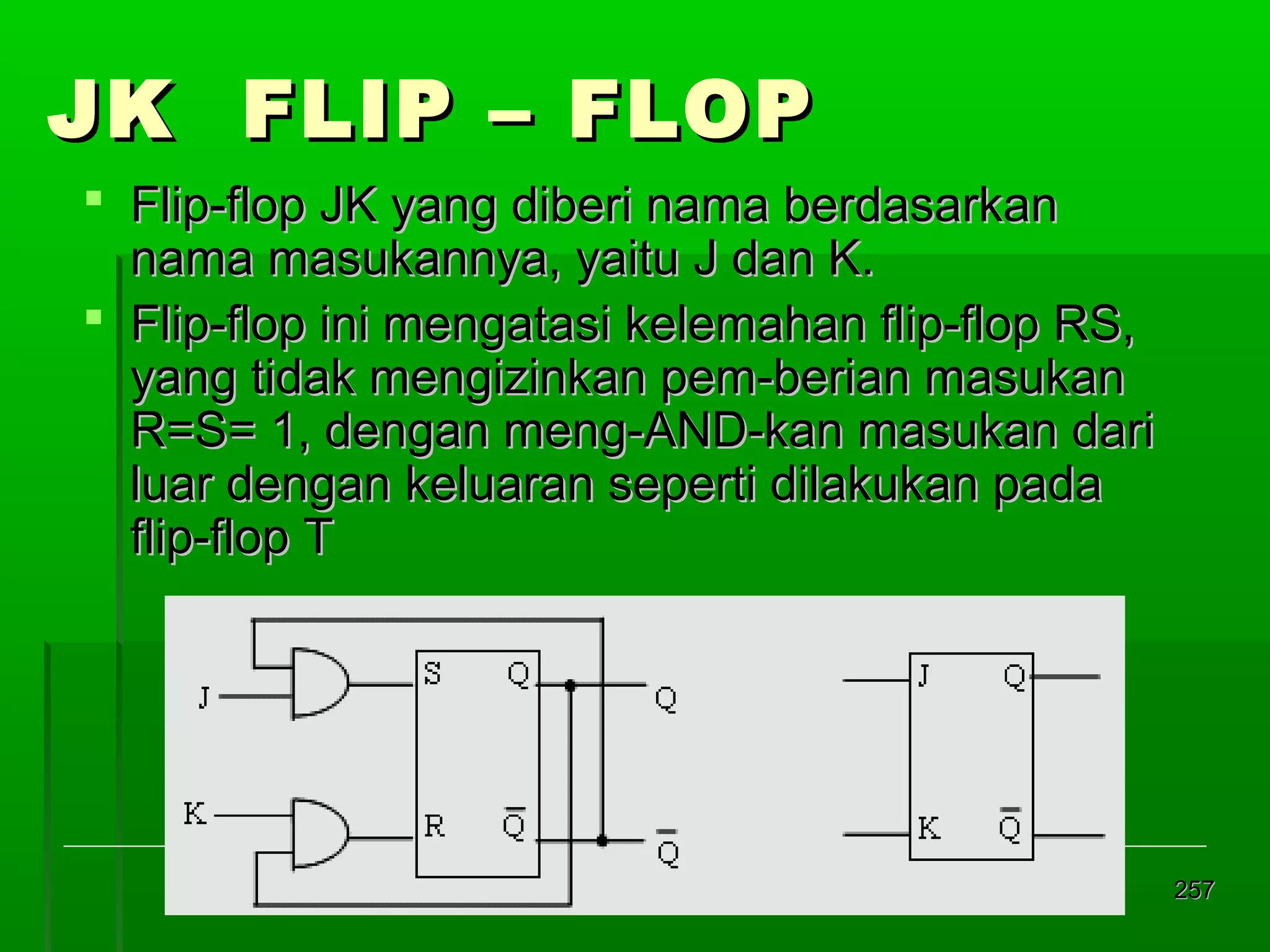

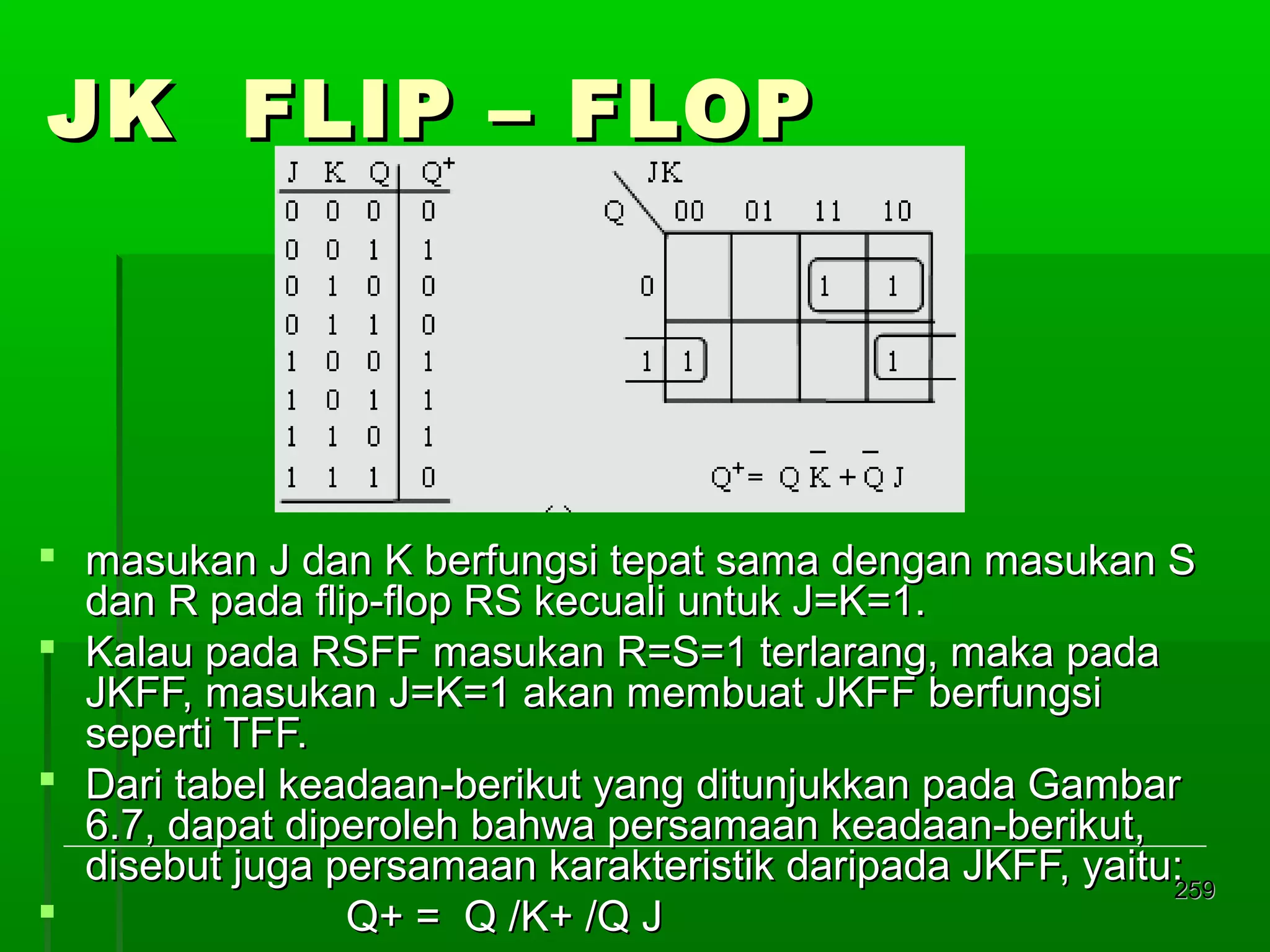
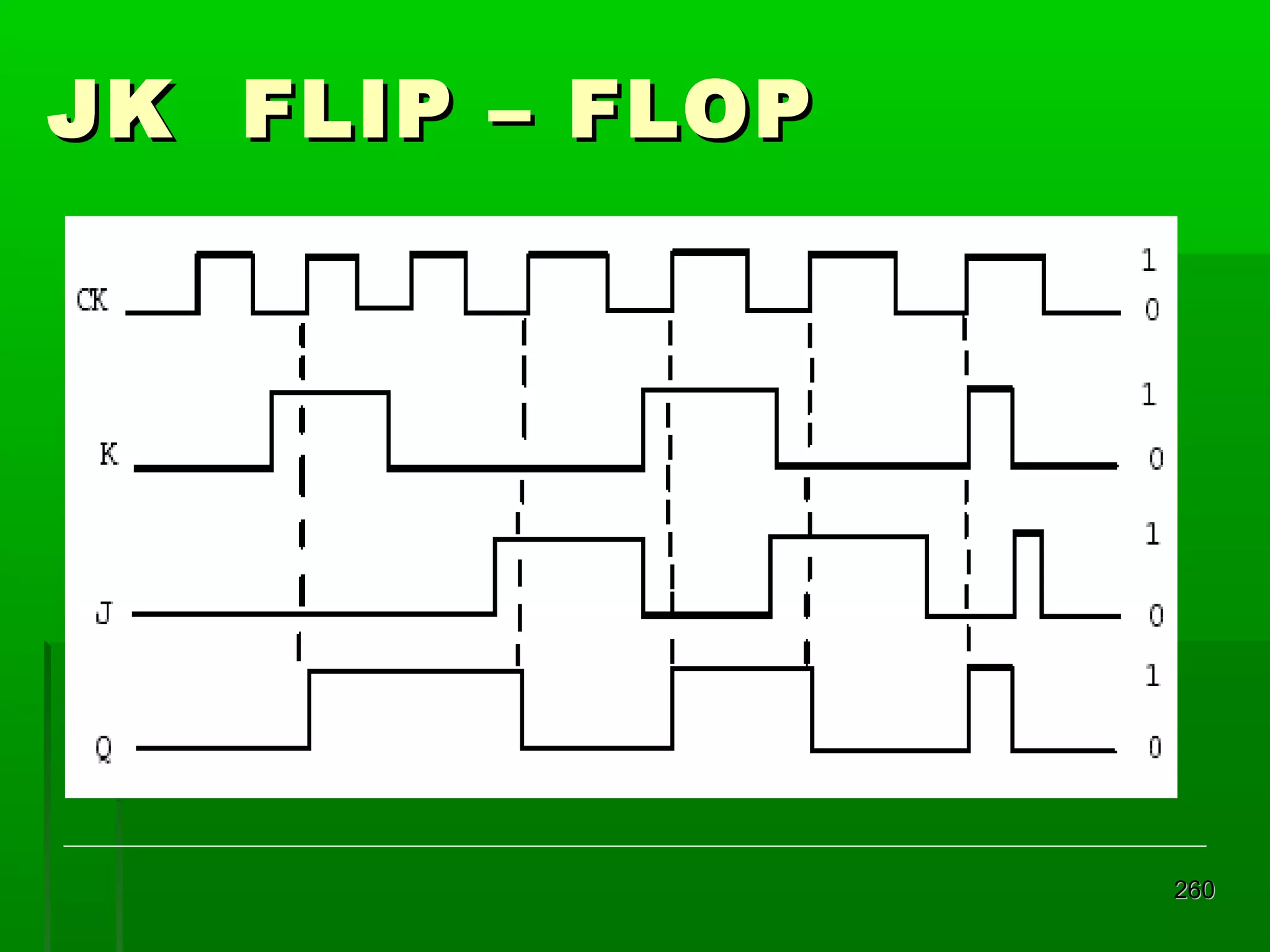




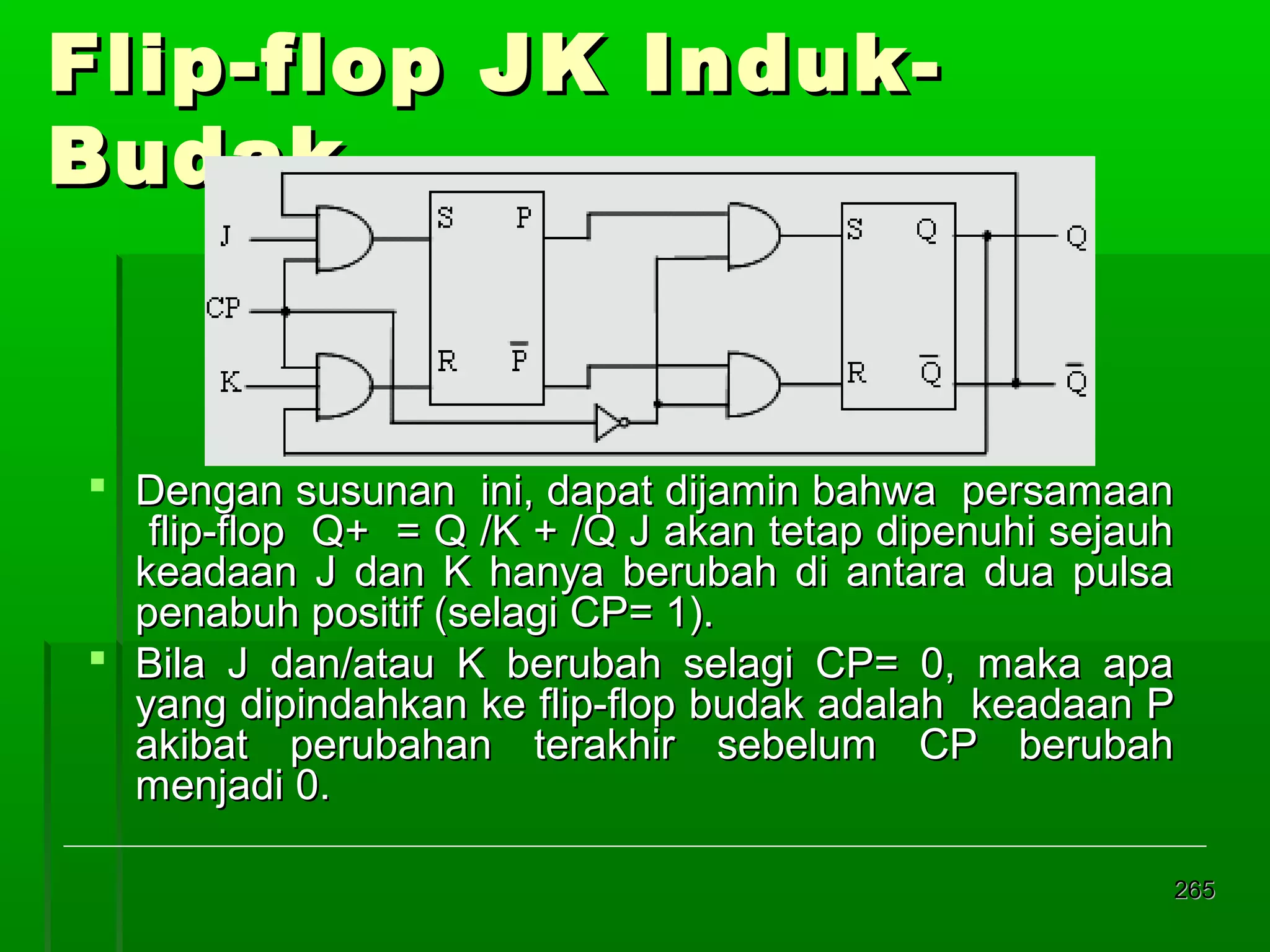

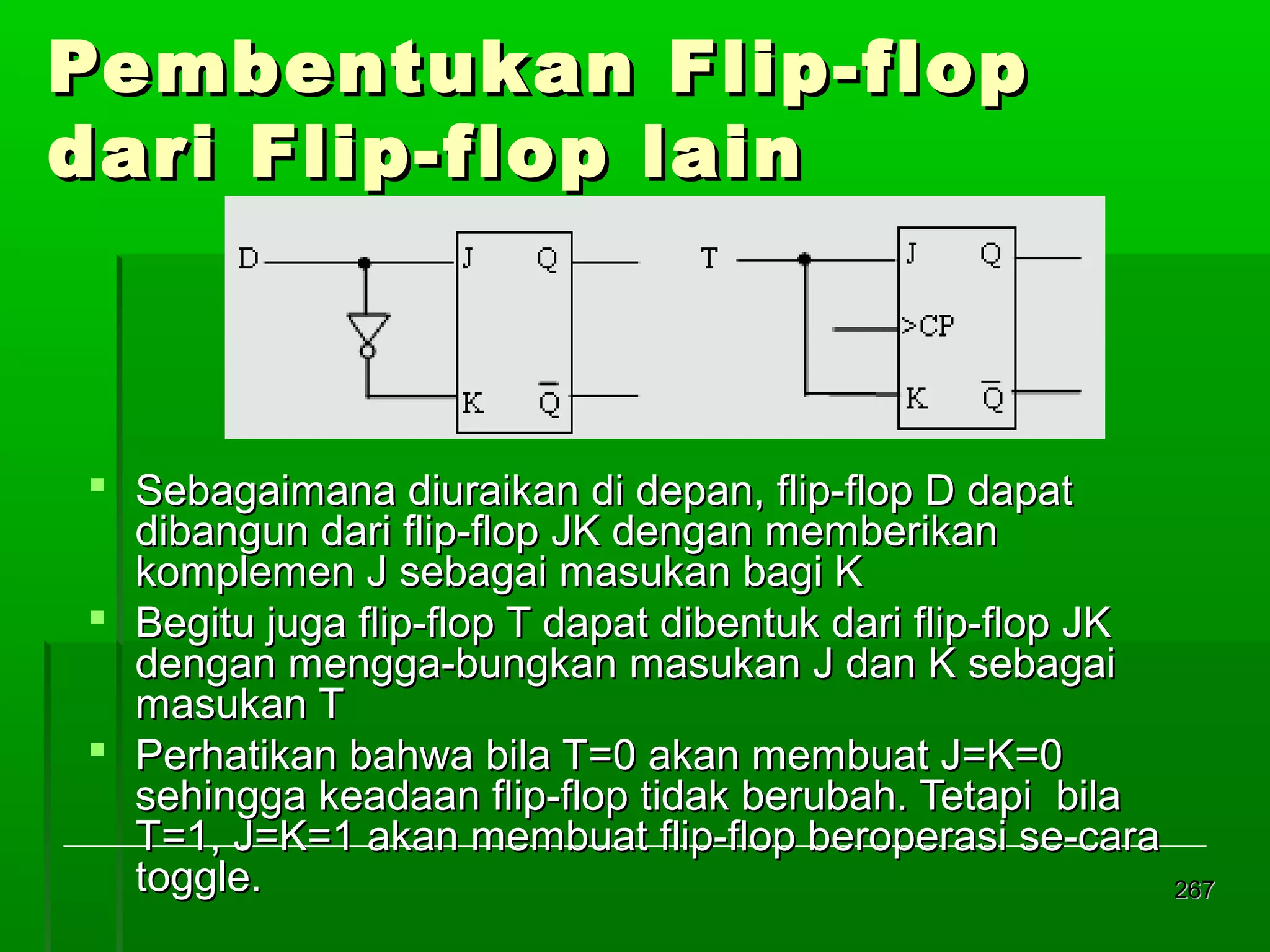








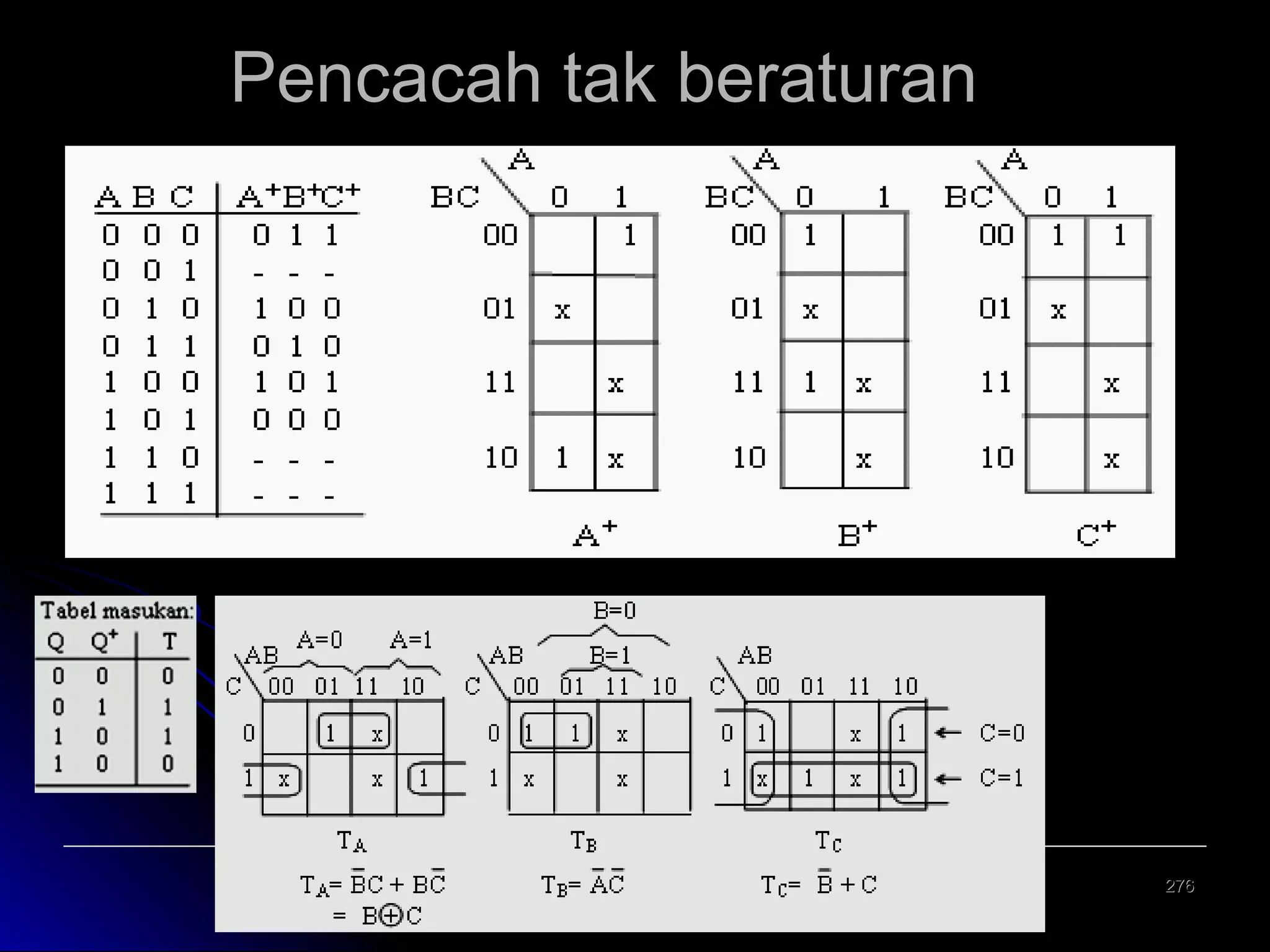
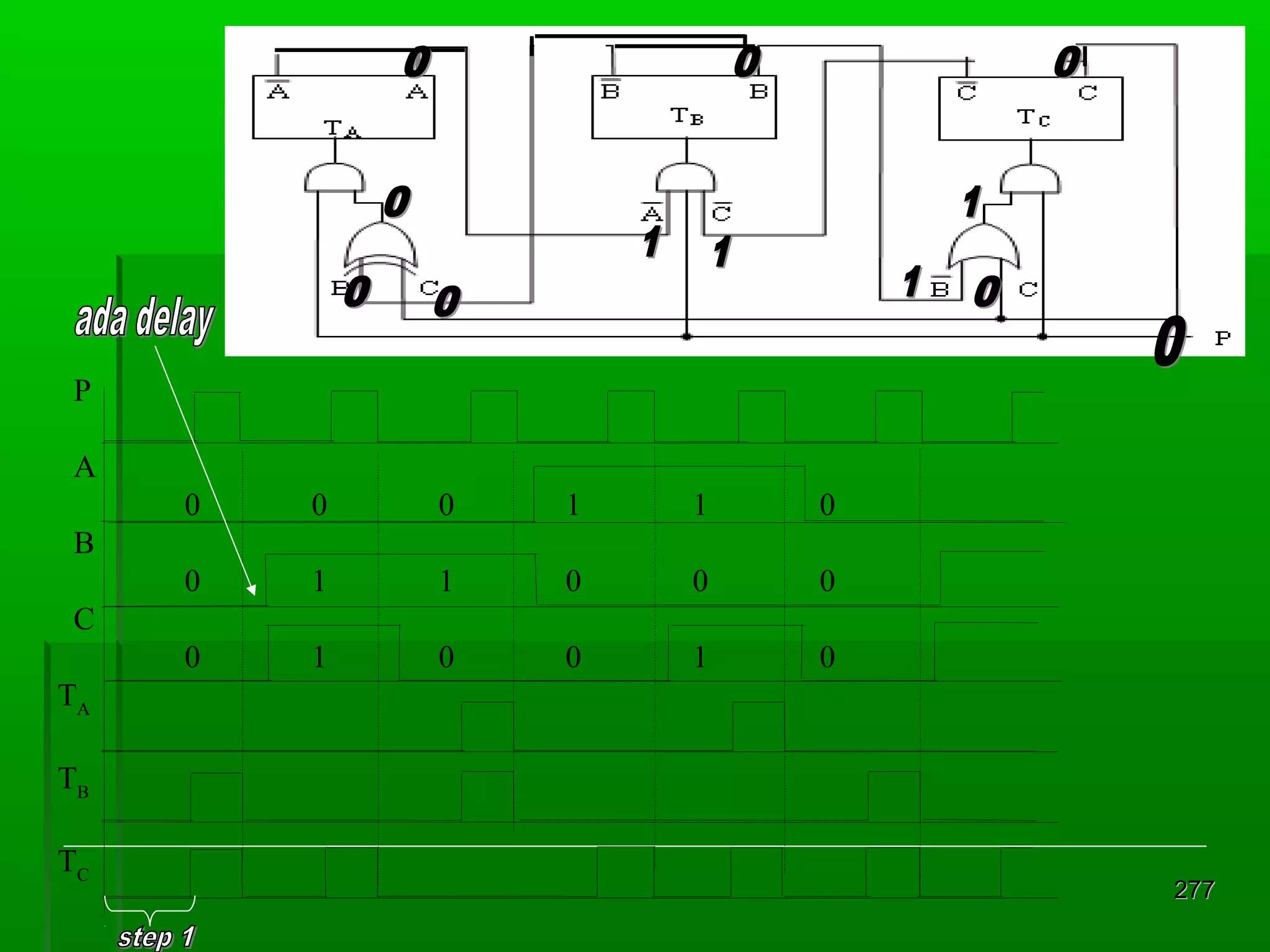
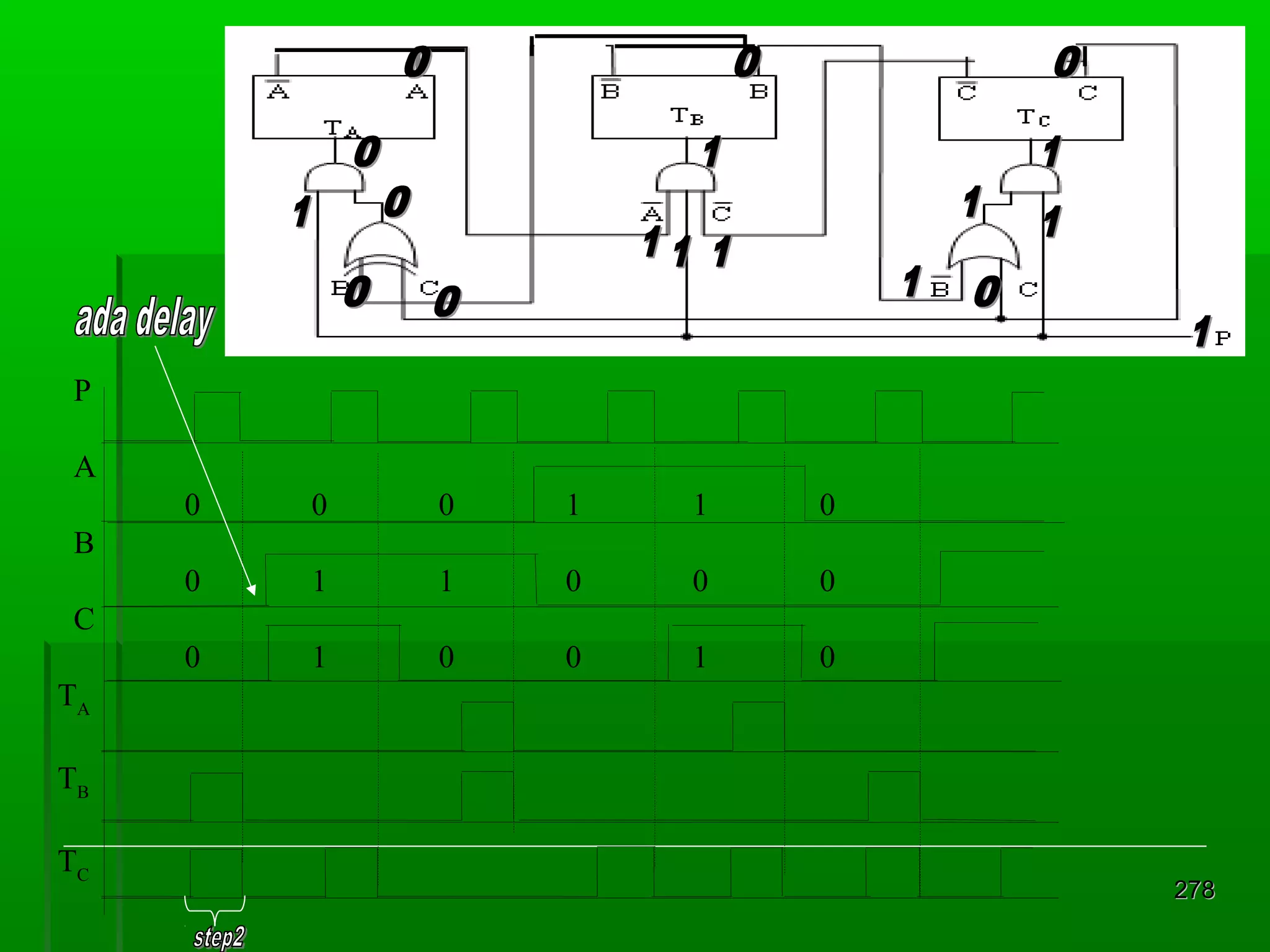

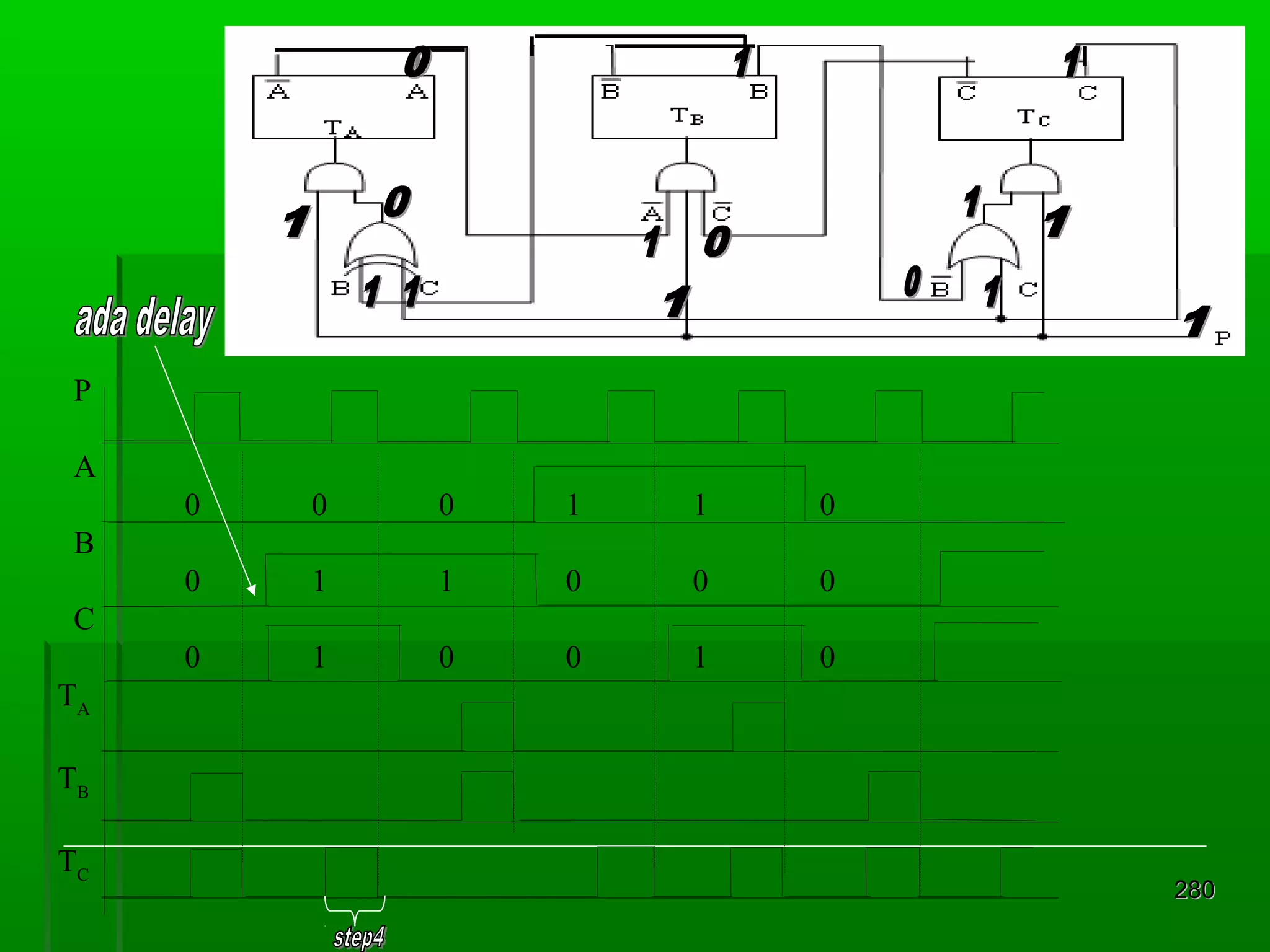

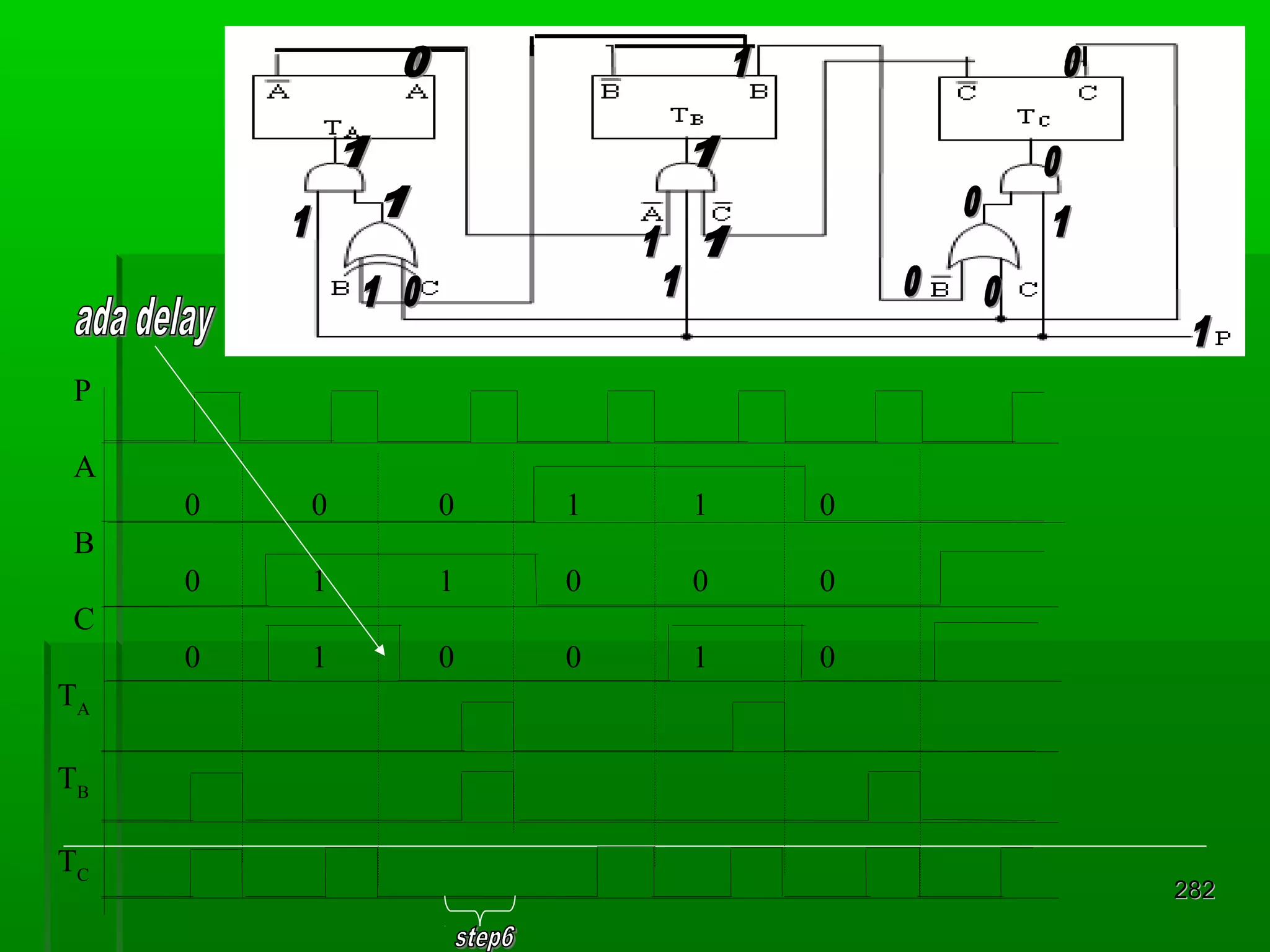




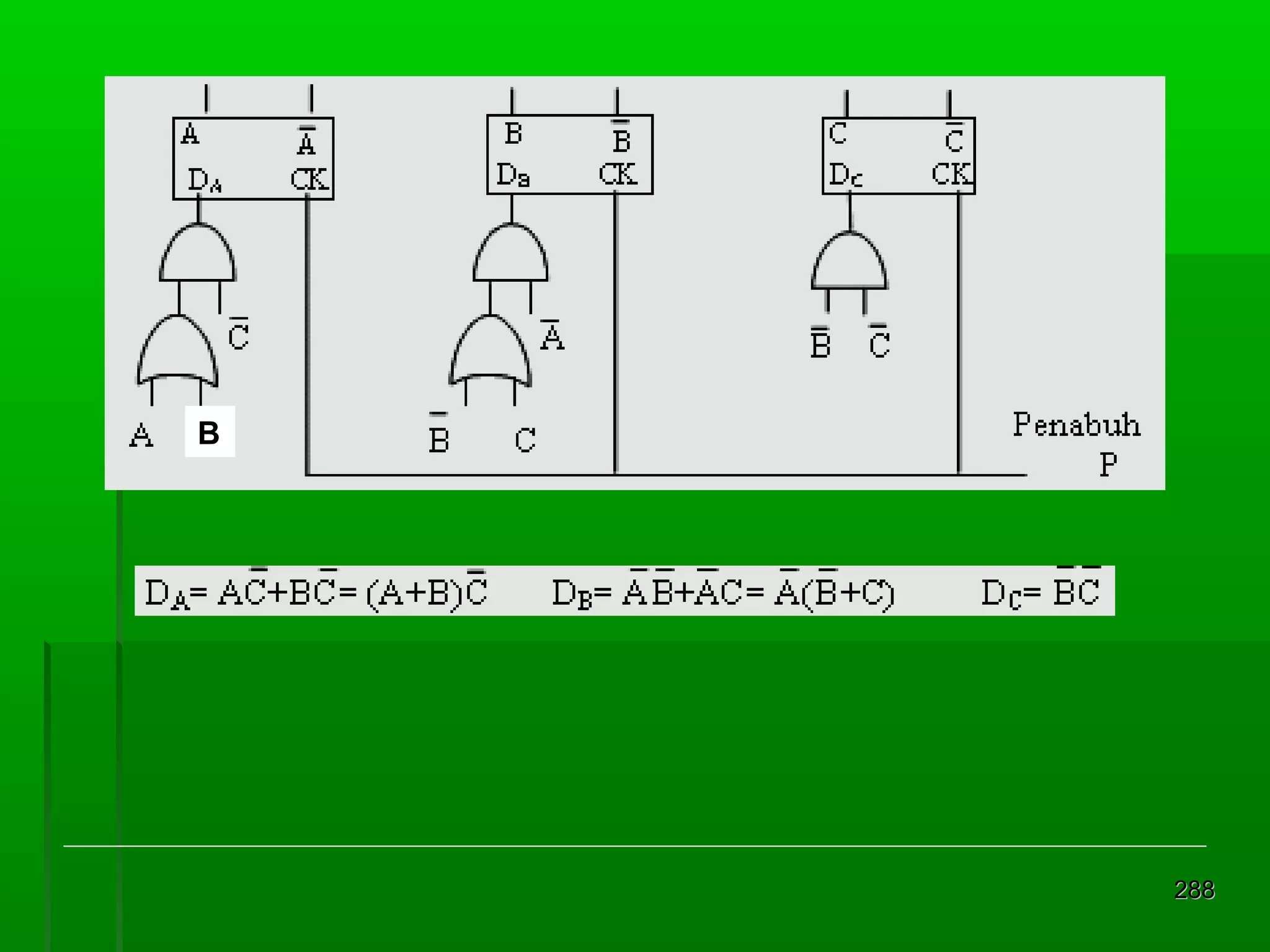








![Re gister Geser Seri [2]
Realisasi : keluaran satu flip-flop
diberikan kepada masukan flip-flop
berikutnya dalam urutan penggeseran
Contoh dengan flip-flop JK 4 bit register
geser:
masukan K = J flip flop D
Din = masukan luar untuk mengganti bit
ujung
299](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-299-2048.jpg)
![Re gister Geser Seri [3]
Rangkaian Logika (atas), bidirectional (bawah)
300](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-300-2048.jpg)

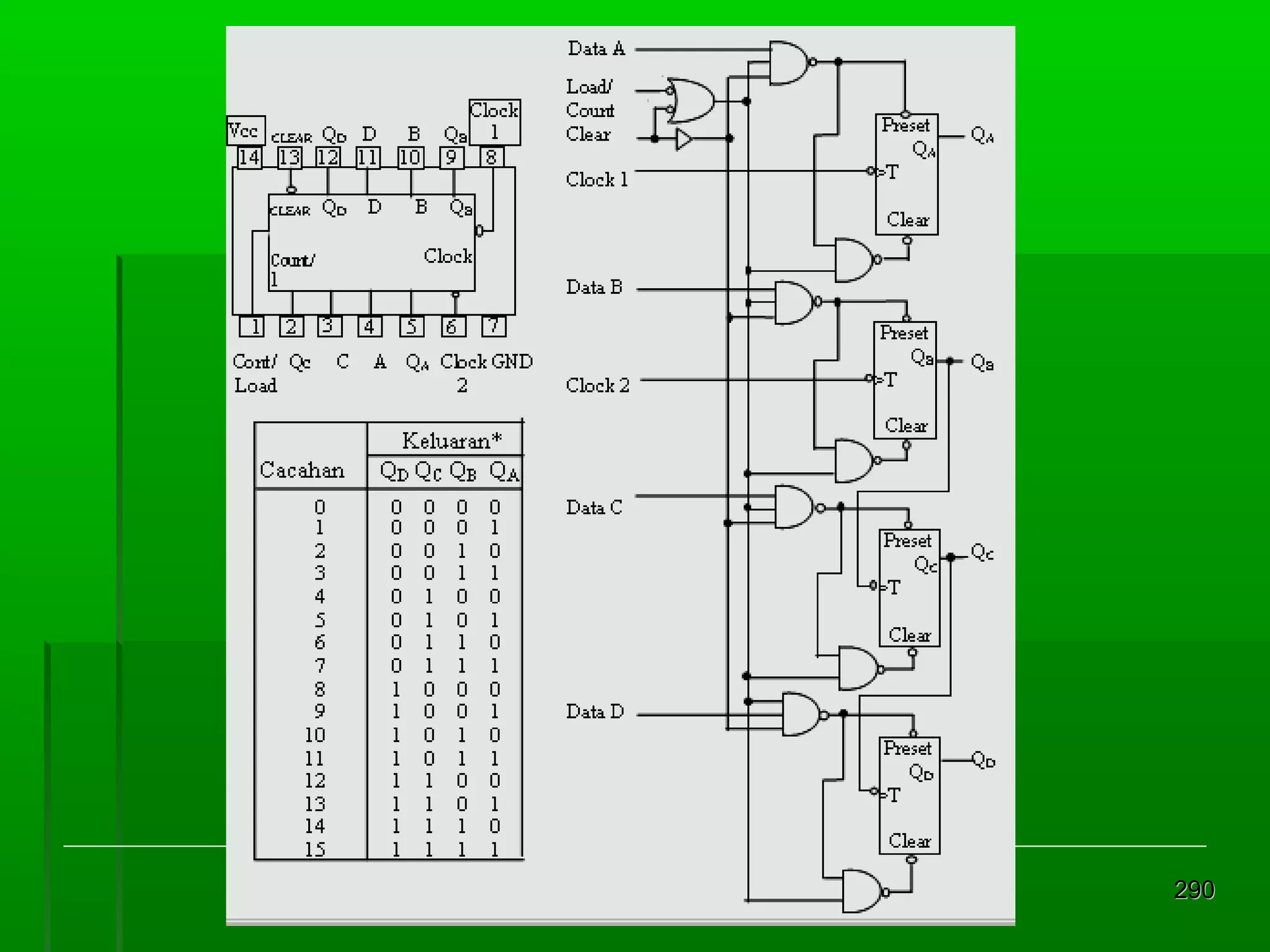
![Re gister Geser Par alel
[2]
Realisasi dengan Flip Flop RS
302](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-302-2048.jpg)











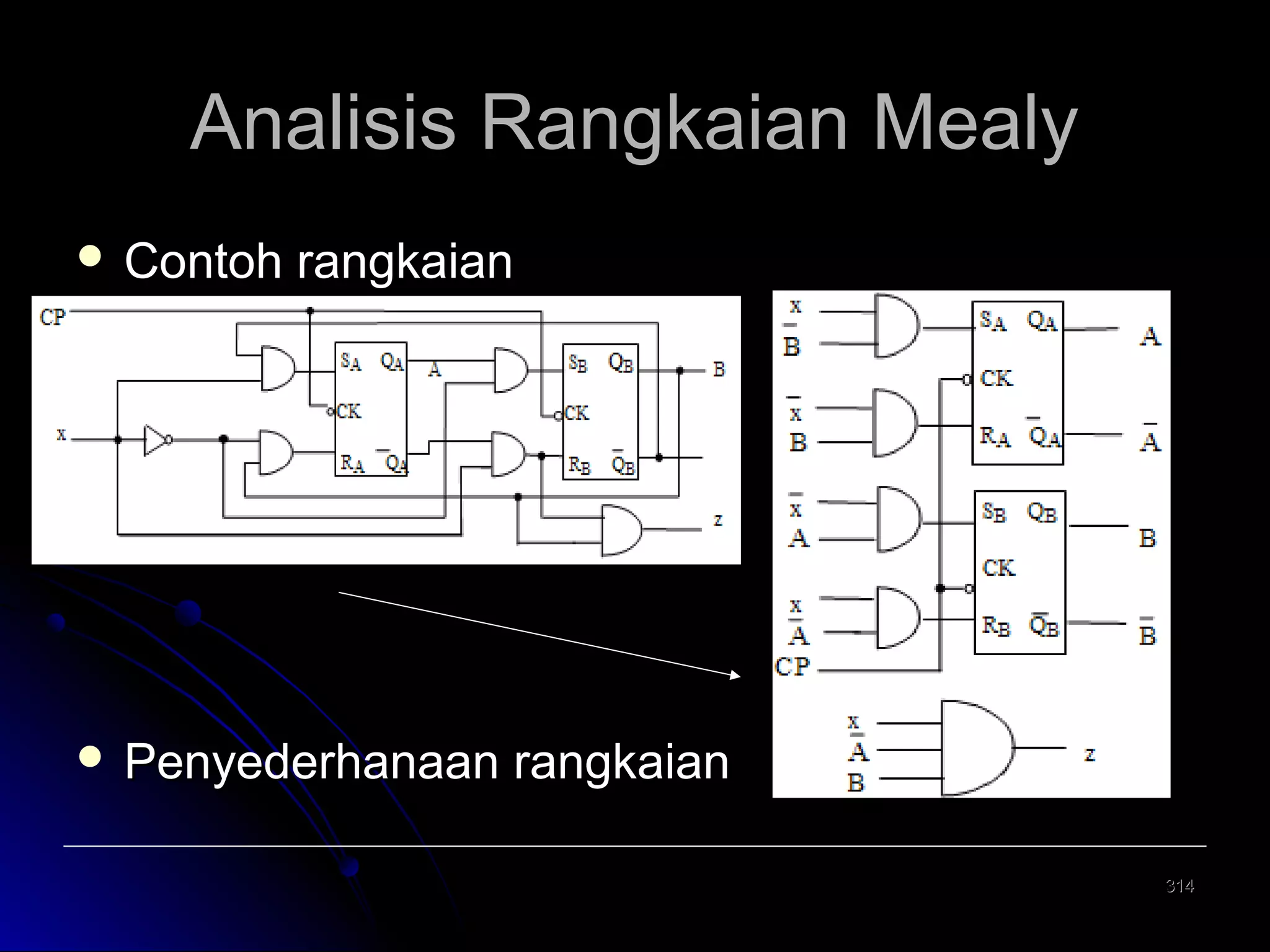
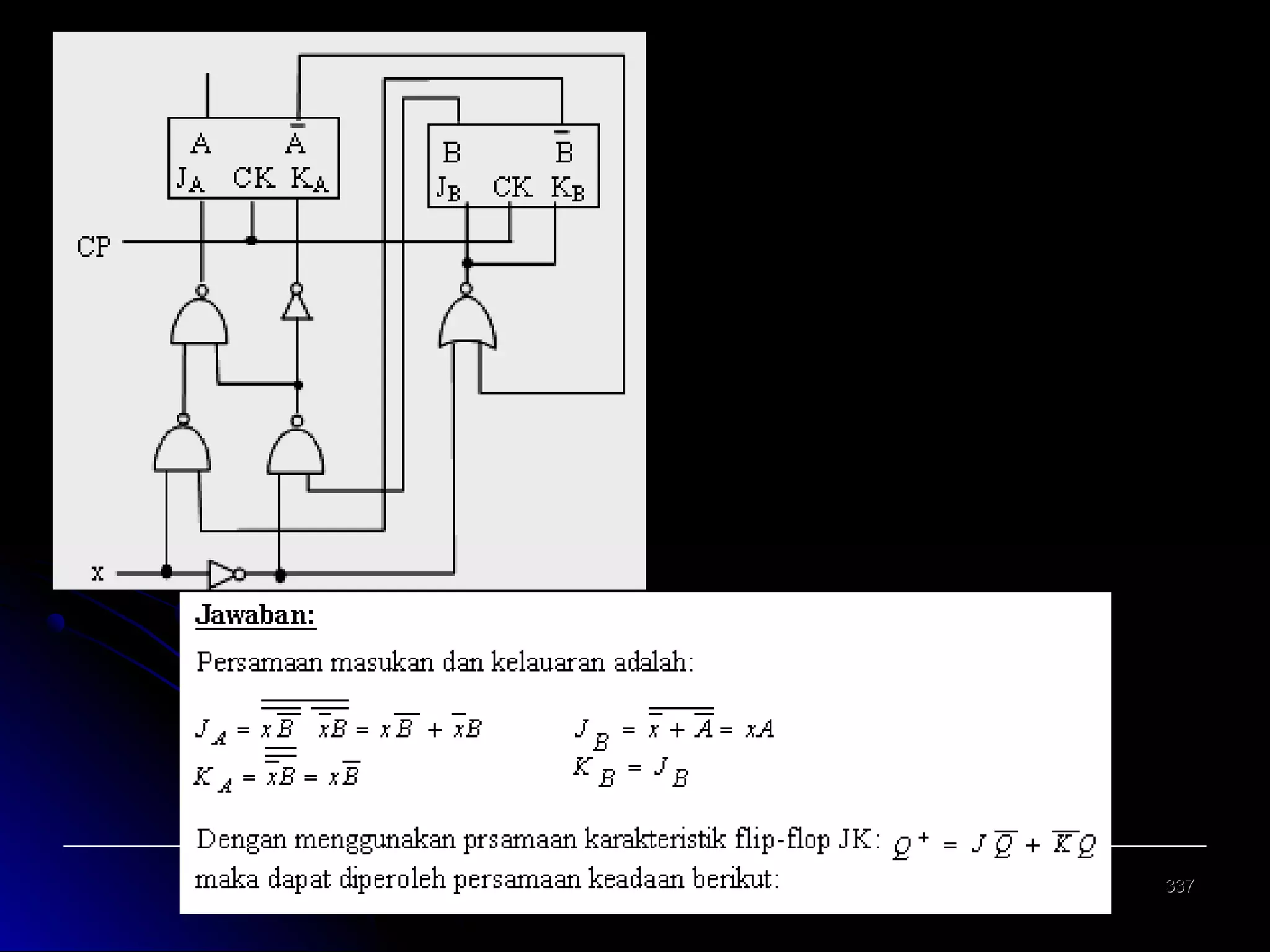
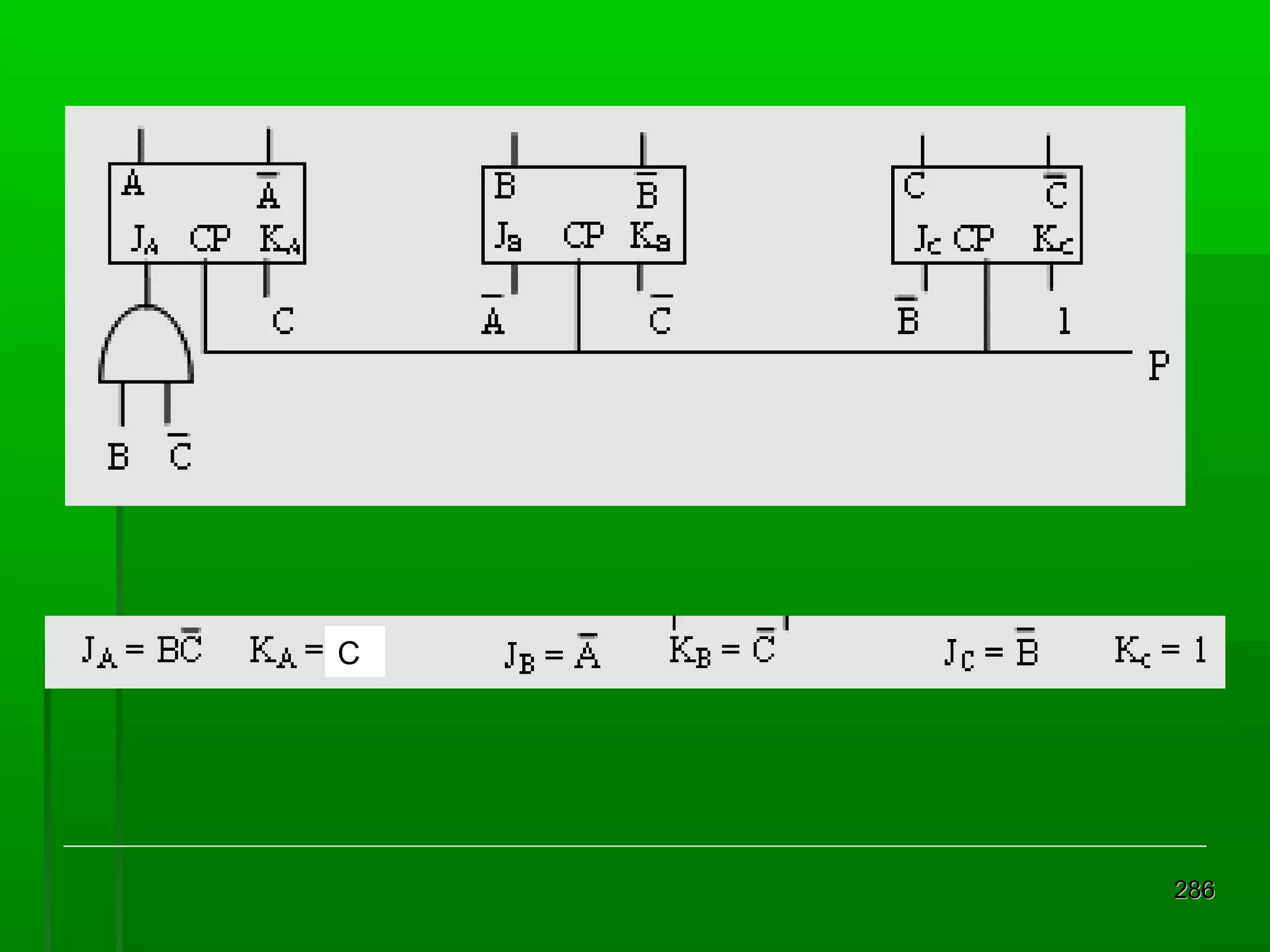
![Analisis Rangkaian Mealy [2]
Persamaan Keadaan
315](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-315-2048.jpg)
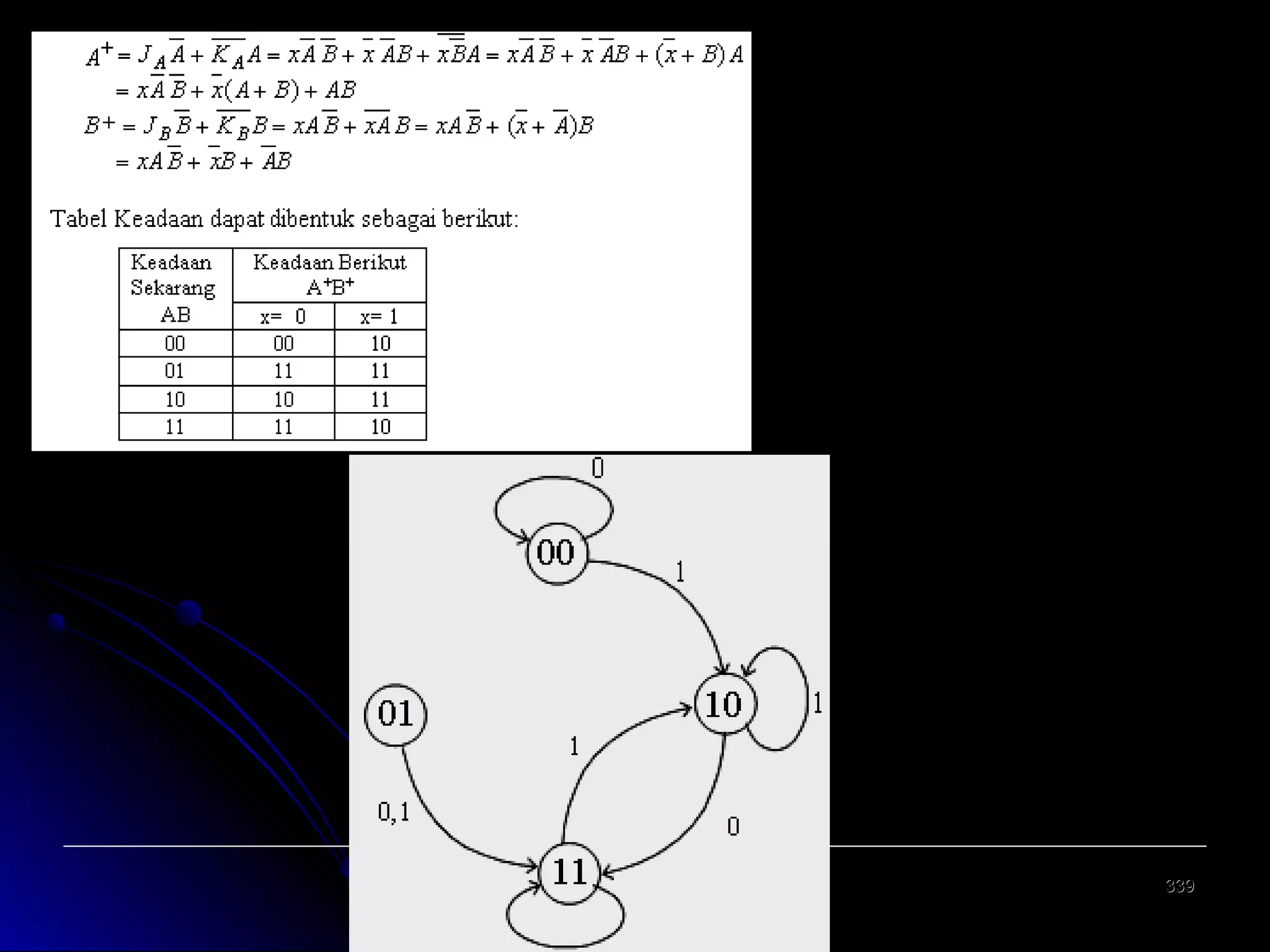
![Analisis Rangkaian Mealy [3]
Tabel Keadaan
dari persamaan keadaan, dapat dibuat sebuah
tabel keadaan dengan masing-masing input 0
dan 1 untuk keluaran berikutnya dan keluaran
rangkaian
316](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-316-2048.jpg)
![Analisis Rangkaian Mealy [4]
317](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-317-2048.jpg)
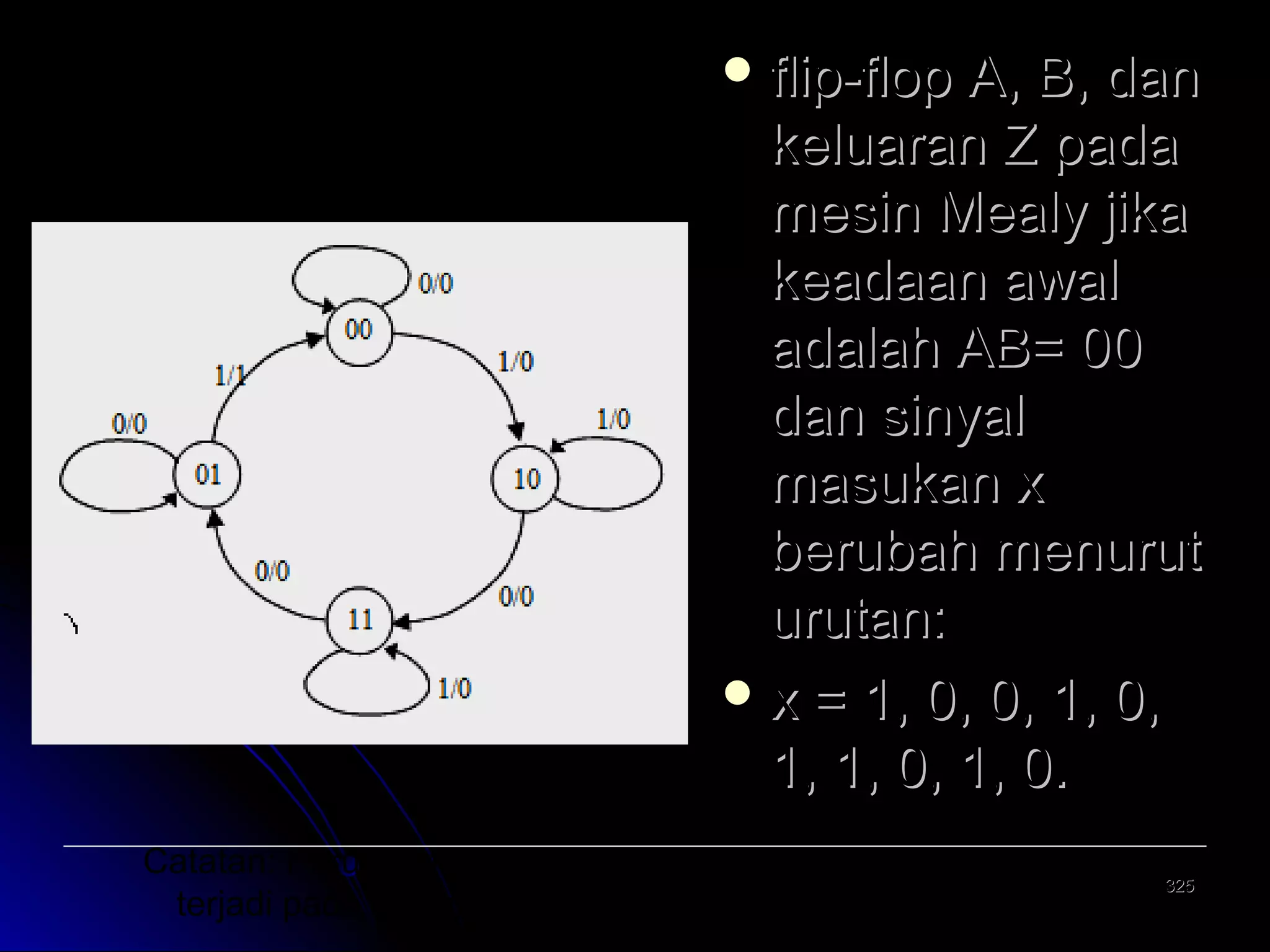
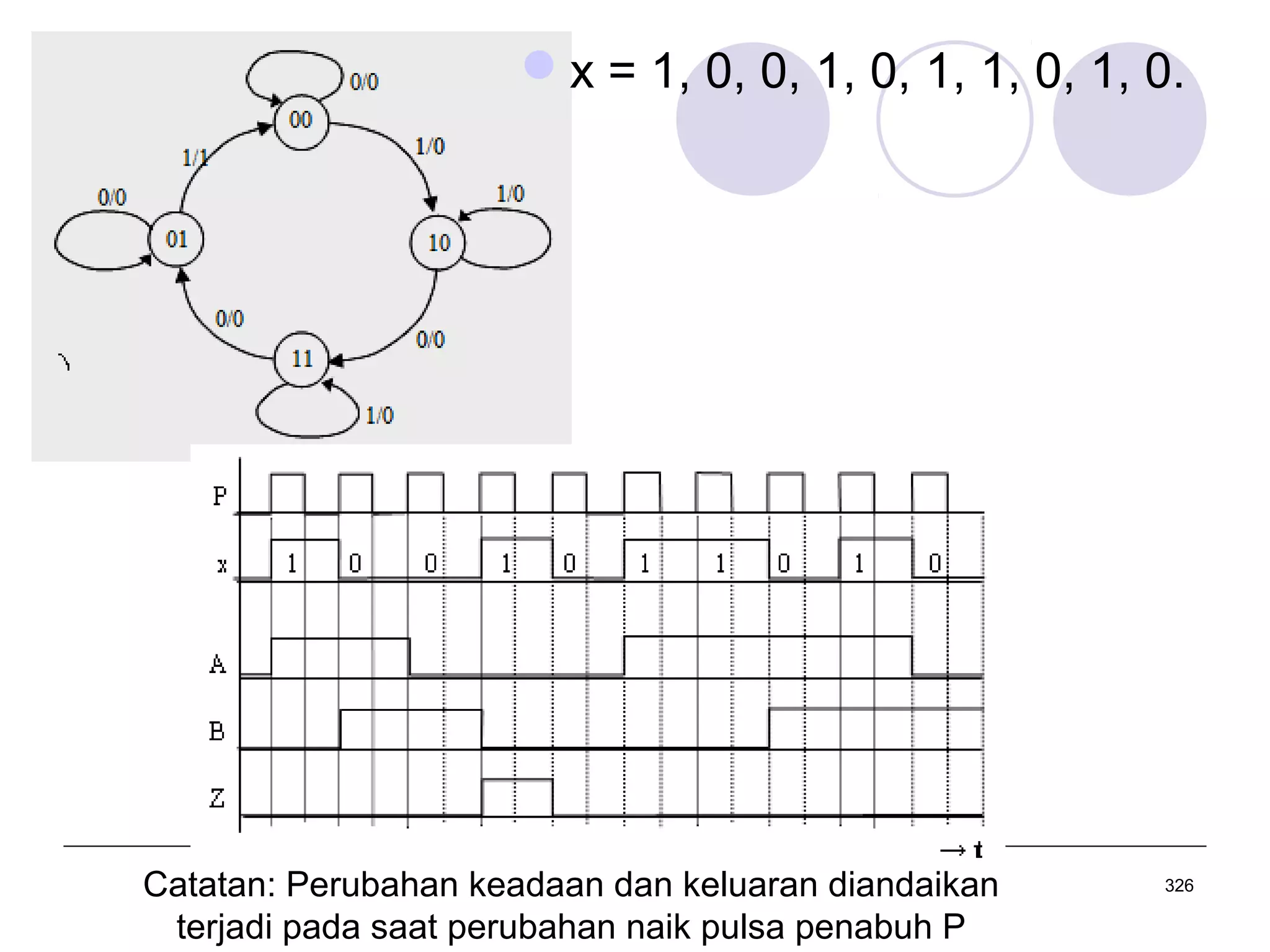
![Analisis Rangkaian Mealy [5]
Diagram Keadaan
di dalam lingkaran : keadaan/state flip flop
di luar lingkaran : input/output rangkaian
318](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-318-2048.jpg)

![Analisis Rangkaian Moore [2]
Persamaan Keadaan
320](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-320-2048.jpg)
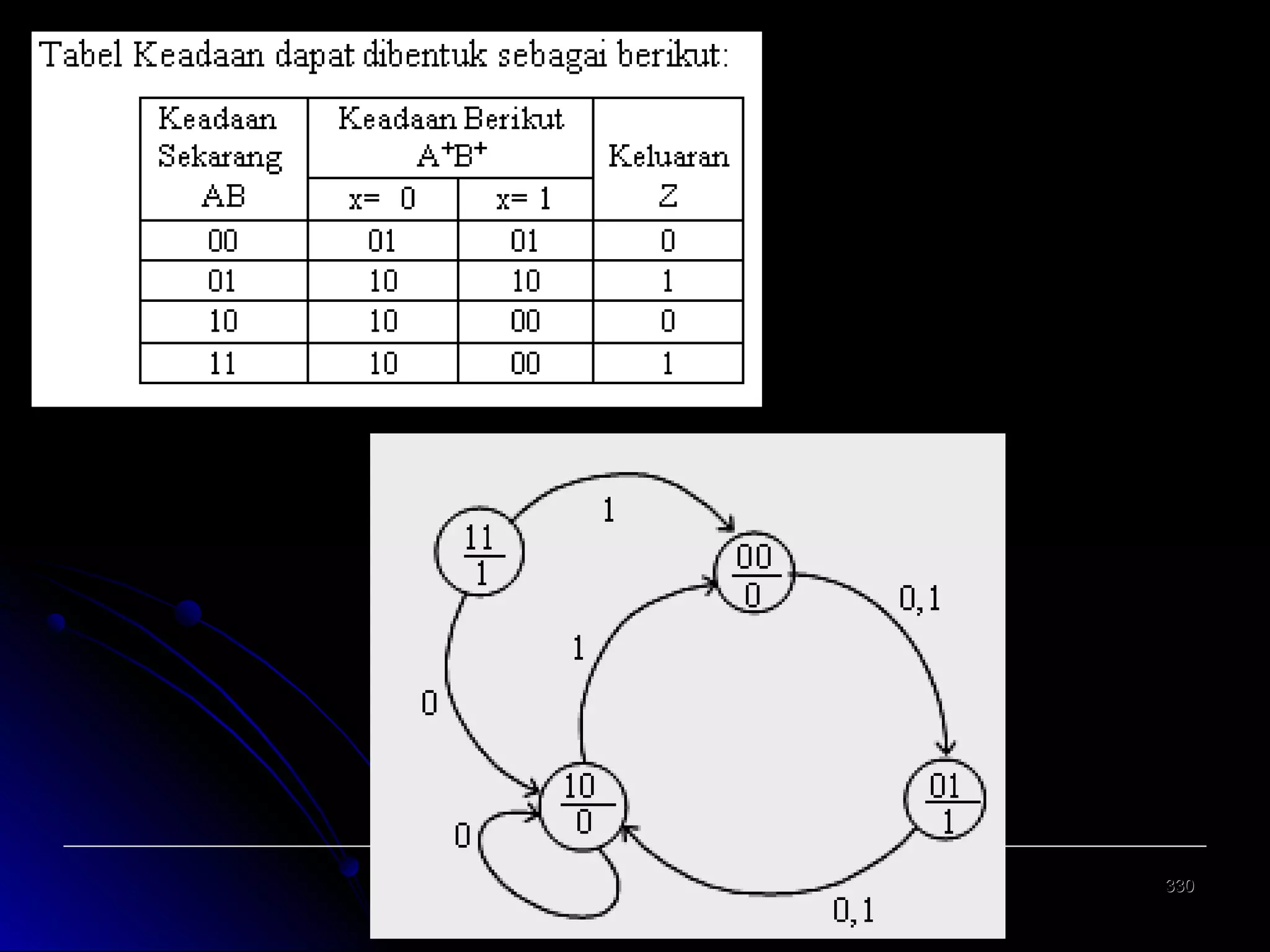
![Analisis Rangkaian Moore [3]
Tabel Keadaan
dari persamaan keadaan, dibuat sebuah tabel
keadaan dengan masing-masing input 0 dan 1
untuk keluaran berikutnya. Sedangkan keluaran
rangkaian hanya bergantung pada
keadaan/state flip flop sekarang
321](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-321-2048.jpg)
![Analisis Rangkaian Moore [3]
322](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-322-2048.jpg)
![Analisis Rangkaian Moore [4]
Diagram Keadaan
di dalam lingkaran :
keadaan(state)flip flop / output rangkaian
di luar lingkaran : input
323](https://image.slidesharecdn.com/bahanttsdantas-131202052054-phpapp01/75/Materi-undig-323-2048.jpg)