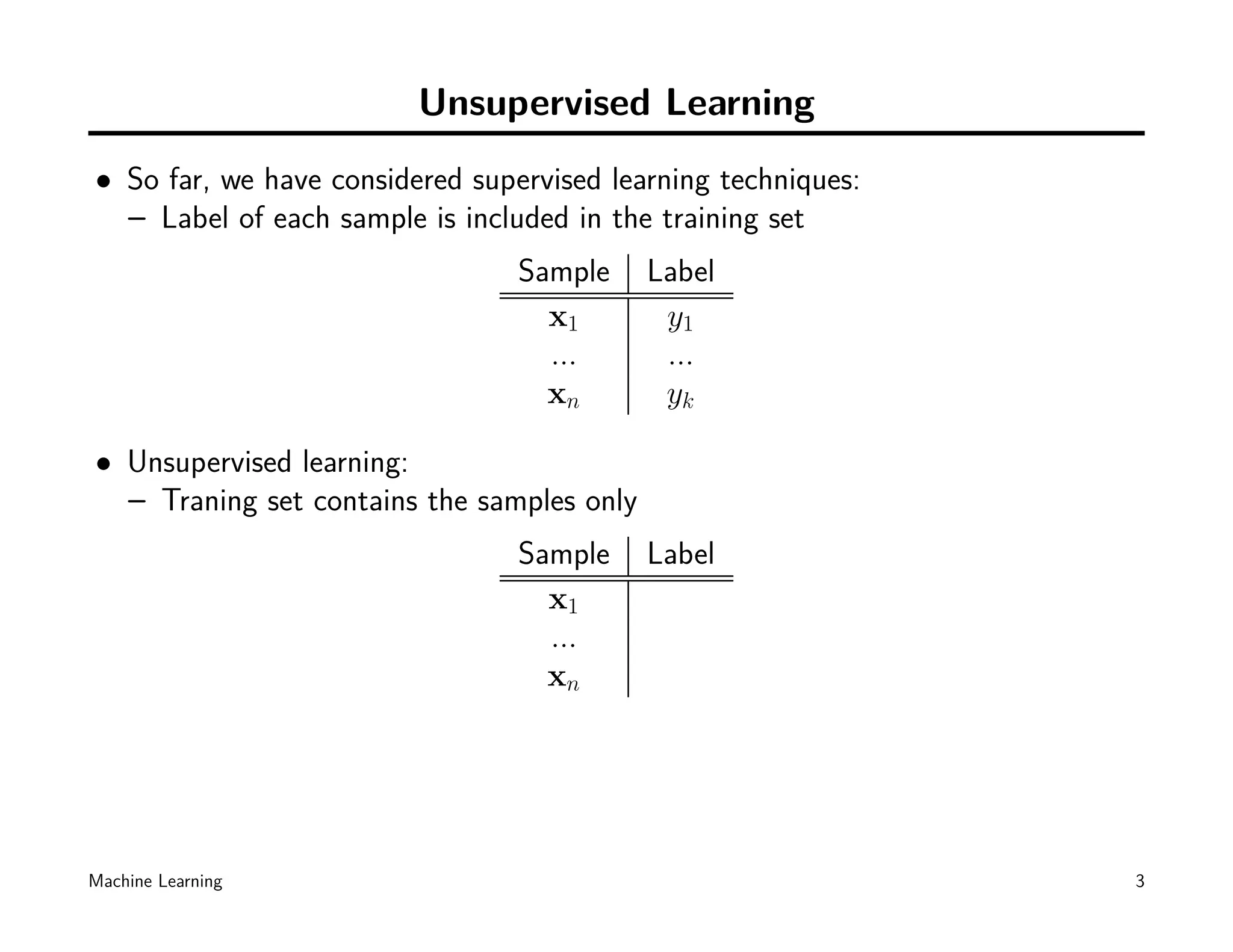
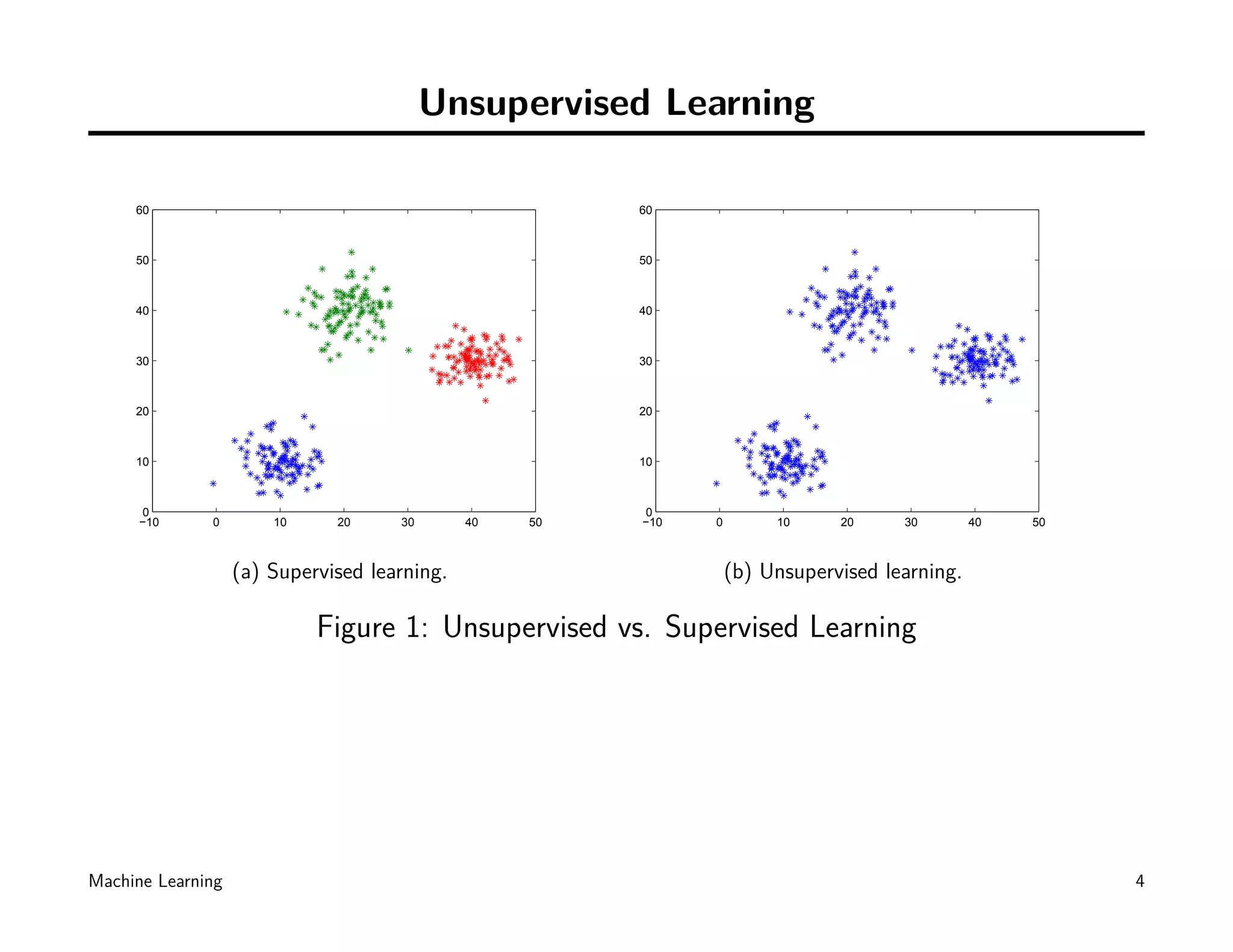
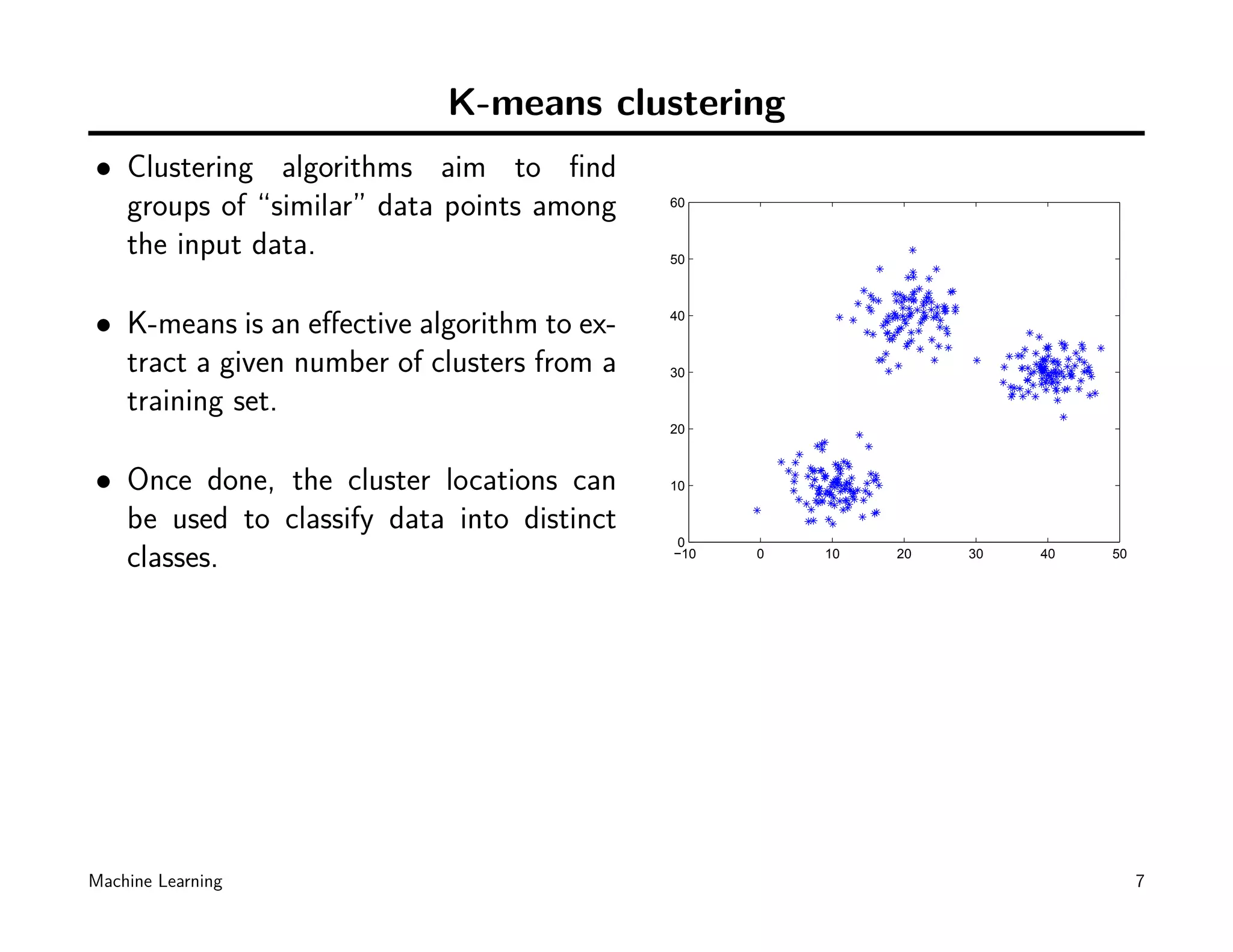
This document discusses machine learning techniques including k-means clustering, expectation maximization (EM), and Gaussian mixture models (GMM). It begins by introducing unsupervised learning problems and k-means clustering. It then describes EM as a general algorithm for maximum likelihood estimation and density estimation. Finally, it discusses using GMM with EM to model data distributions and for classification tasks.

1. Machine Learning
K-means, E.M. and Mixture models
VU Pham
phvu@fit.hcmus.edu.vn
Department of Computer Science
November 22, 2010
Machine Learning

2. Remind: Three Main Problems in ML
• Three main problems in ML:
– Regression: Linear Regression, Neural net...
– Classification: Decision Tree, kNN, Bayessian Classifier...
– Density Estimation: Gauss Naive DE,...
• Today, we will learn:
– K-means: a trivial unsupervised classification algorithm.
– Expectation Maximization: a general algorithm for density estimation.
∗ We will see how to use EM in general cases and in specific case of GMM.
– GMM: a tool for modelling Data-in-the-Wild (density estimator)
∗ We also learn how to use GMM in a Bayessian Classifier
Machine Learning 1

3. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 2

4. Unsupervised Learning
• So far, we have considered supervised learning techniques:
– Label of each sample is included in the training set
Sample Label
x1 y1
... ...
xn yk
• Unsupervised learning:
– Traning set contains the samples only
Sample Label
x1
...
xn
Machine Learning 3

5. Unsupervised Learning
60 60
50 50
40 40
30 30
20 20
10 10
0 0
−10 0 10 20 30 40 50 −10 0 10 20 30 40 50
(a) Supervised learning. (b) Unsupervised learning.
Figure 1: Unsupervised vs. Supervised Learning
Machine Learning 4

6. What is unsupervised learning useful for?
• Collecting and labeling a large training set can be very expensive.
• Be able to find features which are helpful for categorization.
• Gain insight into the natural structure of the data.
Machine Learning 5

7. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 6

8. K-means clustering
• Clustering algorithms aim to find
groups of “similar” data points among 60
the input data. 50
• K-means is an effective algorithm to ex- 40
tract a given number of clusters from a 30
training set.
20
• Once done, the cluster locations can 10
be used to classify data into distinct
0
classes. −10 0 10 20 30 40 50
Machine Learning 7

9. K-means clustering
• Given:
– The dataset: {xn}N = {x1, x2, ..., xN}
n=1
– Number of clusters: K (K < N )
• Goal: find a partition S = {Sk }K so that it minimizes the objective function
k=1
N
∑ K
∑
J= rnk ∥ xn − µk ∥2 (1)
n=1 k=1
where rnk = 1 if xn is assigned to cluster Sk , and rnj = 0 for j ̸= k.
i.e. Find values for the {rnk } and the {µk } to minimize (1).
Machine Learning 8

10. K-means clustering
N
∑ K
∑
J= rnk ∥ xn − µk ∥2
n=1 k=1
• Select some initial values for the µk .
• Expectation: keep the µk fixed, minimize J respect to rnk .
• Maximization: keep the rnk fixed, minimize J respect to the µk .
• Loop until no change in the partitions (or maximum number of interations is
exceeded).
Machine Learning 9

11. K-means clustering
N
∑ K
∑
J= rnk ∥ xn − µk ∥2
n=1 k=1
• Expectation: J is linear function of rnk


1 if k = arg minj ∥ xn − µj ∥2




rnk =


0
 otherwise
• Maximization: setting the derivative of J with respect to µk to zero, gives:
∑
n rnk xn
µk = ∑
n rnk
Convergence of K-means: assured [why?], but may lead to local minimum of J
[8]
Machine Learning 10

12. K-means clustering: How to understand?
N
∑ K
∑
J= rnk ∥ xn − µk ∥2
n=1 k=1
• Expectation: minimize J respect to rnk
– For each xn, find the “closest” cluster mean µk and put xn into cluster Sk .
• Maximization: minimize J respect to µk
– For each cluster Sk , re-estimate the cluster mean µk to be the average value
of all samples in Sk .
• Loop until no change in the partitions (or maximum number of interations is
exceeded).
Machine Learning 11

13. K-means clustering: Demonstration
Machine Learning 12

14. K-means clustering: some variations
• Initial cluster centroids:
– Randomly selected
– Iterative procedure: k-mean++ [2]
• Number of clusters K:
√
– Empirically/experimentally: 2 ∼ n
– Learning [6]
• Objective function:
– General dissimilarity measure: k-medoids algorithm.
• Speeding up:
– kd-trees for pre-processing [7]
– Triangle inequality for distance calculation [4]
Machine Learning 13

15. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 14

16. Expectation Maximization
E.M.
Machine Learning 15

17. Expectation Maximization
• A general-purpose algorithm for MLE in a wide range of situations.
• First formally stated by Dempster, Laird and Rubin in 1977 [1]
– We even have several books discussing only on EM and its variations!
• An excellent way of doing our unsupervised learning problem, as we will see
– EM is also used widely in other domains.
Machine Learning 16

18. EM: a solution for MLE
• Given a statistical model with:
– a set X of observed data,
– a set Z of unobserved latent data,
– a vector of unknown parameters θ,
– a likelihood function L (θ; X, Z) = p (X, Z | θ)
• Roughly speaking, the aim of MLE is to determine θ = arg maxθ L (θ; X, Z)
– We known the old trick: partial derivatives of the log likelihood...
– But it is not always tractable [e.g.]
– Other solutions are available.
Machine Learning 17

19. EM: General Case
L (θ; X, Z) = p (X, Z | θ)
• EM is just an iterative procedure for finding the MLE
• Expectation step: keep the current estimate θ (t) fixed, calculate the expected
value of the log likelihood function
( )
Q θ|θ (t)
= E [log L (θ; X, Z)] = E [log p (X, Z | θ)]
• Maximization step: Find the parameter that maximizes this quantity
( )
θ (t+1)
= arg max Q θ | θ (t)
θ
Machine Learning 18

20. EM: Motivation
• If we know the value of the parameters θ, we can find the value of latent variables
Z by maximizing the log likelihood over all possible values of Z
– Searching on the value space of Z.
• If we know Z, we can find an estimate of θ
– Typically by grouping the observed data points according to the value of asso-
ciated latent variable,
– then averaging the values (or some functions of the values) of the points in
each group.
To understand this motivation, let’s take K-means as a trivial example...
Machine Learning 19

21. EM: informal description
Both θ and Z are unknown, EM is an iterative algorithm:
1. Initialize the parameters θ to some random values.
2. Compute the best values of Z given these parameter values.
3. Use the just-computed values of Z to find better estimates for θ.
4. Iterate until convergence.
Machine Learning 20

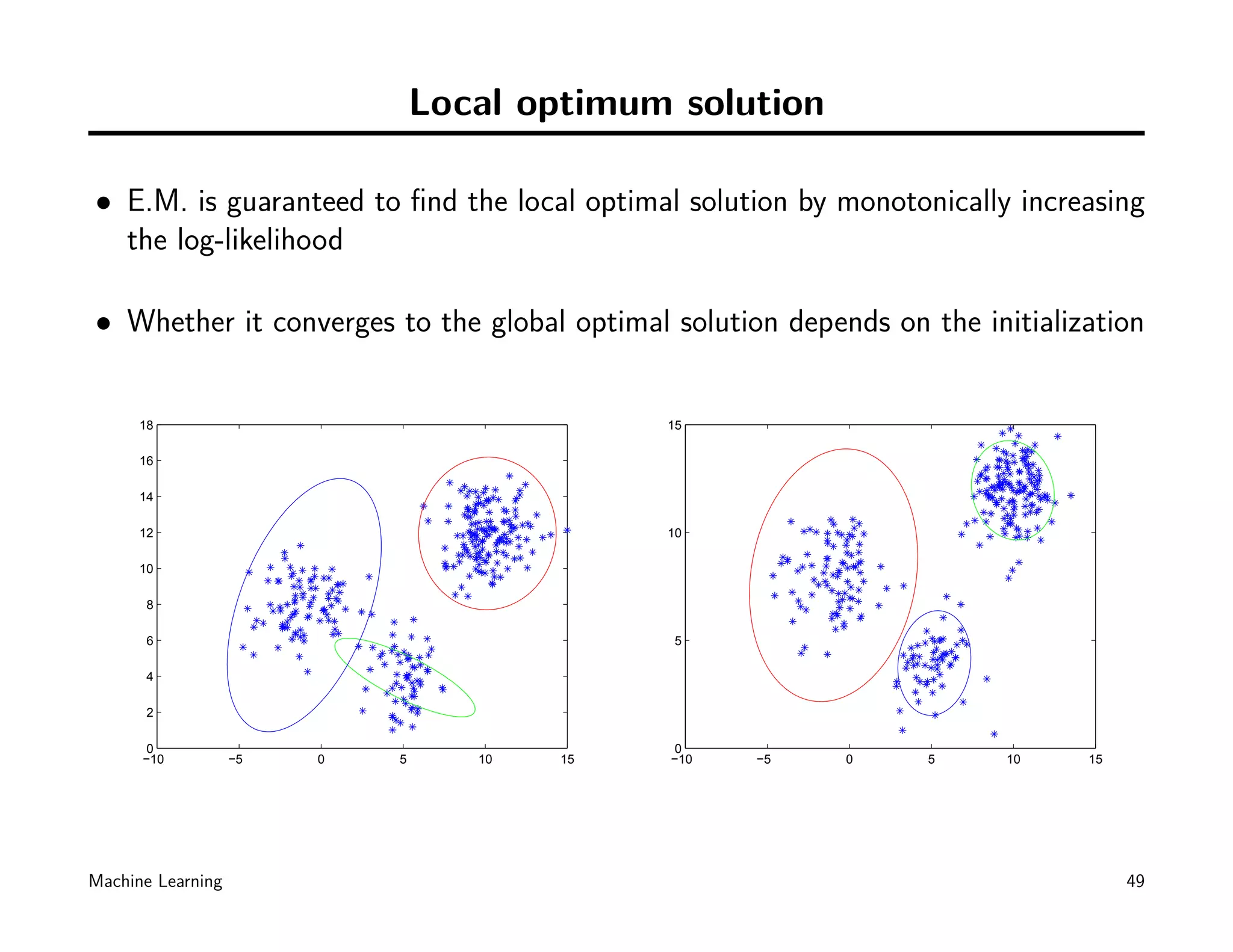
22. EM Convergence
• E.M. Convergence: Yes
– After each iteration, p (X, Z | θ) must increase or remain [NOT OBVIOUS]
– But it can not exceed 1 [OBVIOUS]
– Hence it must converge [OBVIOUS]
• Bad news: E.M. converges to local optimum.
– Whether the algorithm converges to the global optimum depends on the ini-
tialization.
• Let’s take K-means as an example, again...
• Details can be found in [9].
Machine Learning 21

23. Regularized EM (REM)
• EM tries to inference the latent (missing) data Z from the observations X
– We want to choose the missing data that has a strong probabilistic relation
to the observations, i.e. we assume that the observations contains lots of
information about the missing data.
– But E.M. does not have any control on the relationship between the missing
data and the observations!
• Regularized EM (REM) [5] tries to optimized the penalized likelihood
L (θ | X, Z) = L (θ | X, Z) − γH (Z | X, θ)
where H (Y ) is Shannon’s entropy of the random variable Y :
∑
H (Y ) = − p (y) log p (y)
y
and the positive value γ is the regularization parameter. [When γ = 0?]
Machine Learning 22

24. Regularized EM (REM)
• E-step: unchanged
• M-step: Find the parameter that maximizes this quantity
( )
θ (t+1)
= arg max Q θ | θ (t)
θ
where ( ) ( )
Q θ|θ (t)
=Q θ|θ (t)
− γH (Z | X, θ)
• REM is expected to converge faster than EM (and it does!)
• So, to apply REM, we just need to determine the H (·) part...
Machine Learning 23

25. Model Selection
• Considering a parametric model:
– When estimating model parameters using MLE, it is possible to increase the
likelihood by adding parameters
– But may result in over-fitting.
• e.g. K-means with different values of K...
• Need a criteria for model selection, e.g. to “judge” which model configuration is
better, how many parameters is sufficient...
– Cross Validation
– Akaike Information Criterion (AIC)
– Bayesian Factor
∗ Bayesian Informaction Criterion (BIC)
∗ Deviance Information Criterion
– ...
Machine Learning 24

26. Bayesian Information Criterion
( ) # of param
BIC = − log p data | θ + log n
2
• Where:
– θ:( the estimated parameters.
)
– p data | θ : the maximized value of the likelihood function for the estimated
model.
– n: number of data points.
– Note that there are other ways to write the BIC expression, but they are all
equivalent.
• Given any two estimated models, the model with the lower value of BIC is
preferred.
Machine Learning 25

27. Bayesian Score
• BIC is an asymptotic (large n) approximation to better (and hard to evaluate)
Bayesian score ˆ
Bayesian score = p (θ) p (data | θ) dθ
θ
• Given two models, the model selection is based on Bayes factor
ˆ
p (θ1) p (data | θ1) dθ1
K = ˆθ1
p (θ2) p (data | θ2) dθ2
θ2
Machine Learning 26

28. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 27

29. Remind: Bayes Classifier
70
60
50
40
30
20
10
0
−10
0 10 20 30 40 50 60 70 80
p (x | y = i) p (y = i)
p (y = i | x) =
p (x)
Machine Learning 28

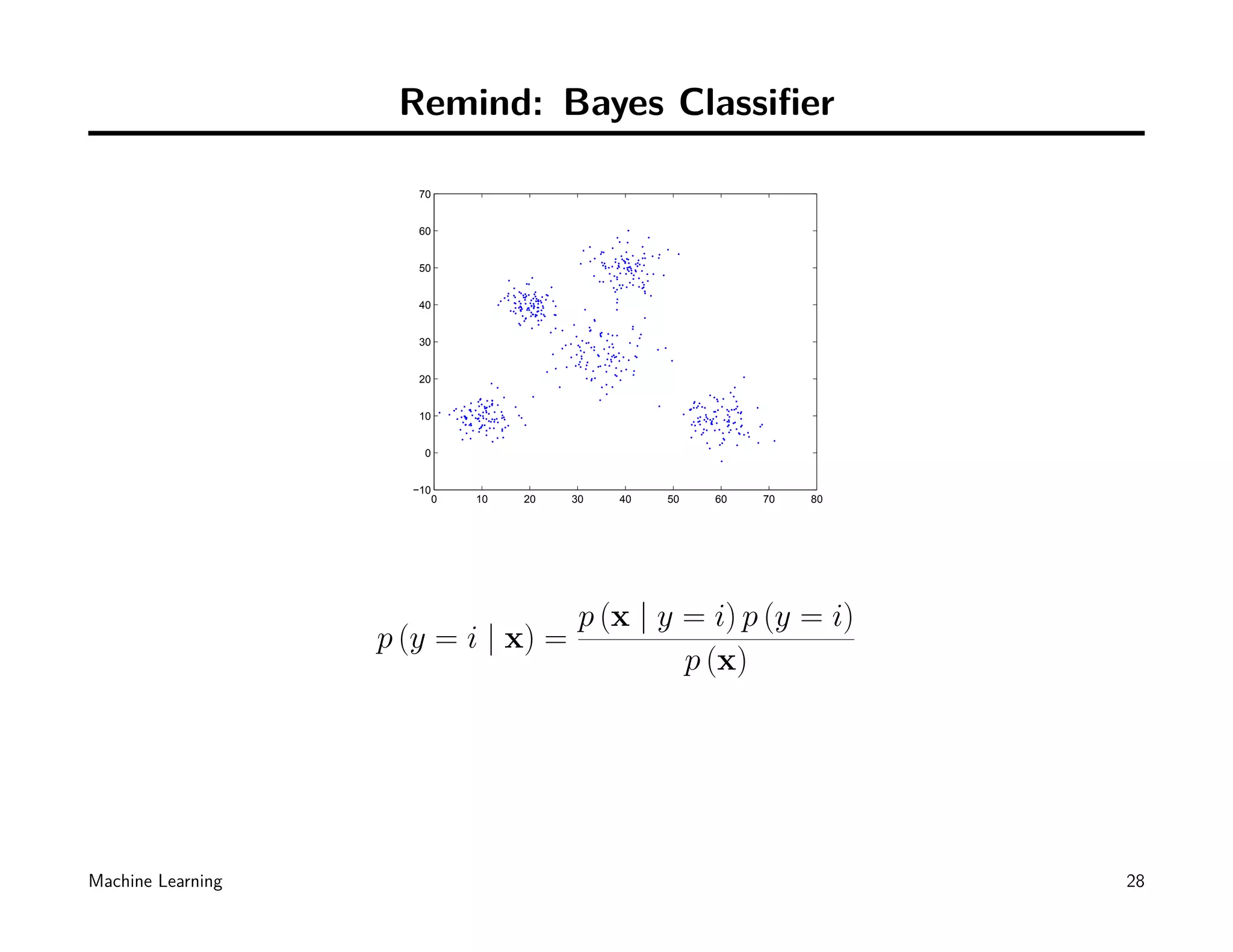
30. Remind: Bayes Classifier
70
60
50
40
30
20
10
0
−10
0 10 20 30 40 50 60 70 80
In case of Gaussian Bayes Classifier:
[ ]
T
d/2
1
exp −2
1
(x − µi) Σi (x − µi) pi
(2π) ∥Σi ∥1/2
p (y = i | x) =
p (x)
How can we deal with the denominator p (x)?
Machine Learning 29

31. Remind: The Single Gaussian Distribution
• Multivariate Gaussian
 
1 1
N (x; µ, Σ) = d/2 exp −

(x − µ)T Σ−1 (x − µ)

(2π) ∥ Σ ∥1/2 2
• For maximum likelihood
∂ ln N (x1, x2, ..., xN; µ, Σ)
0=
∂µ
• and the solution is
1 N
∑
µM L = xi
N i=1
1 N
∑
ΣM L = (xi − µM L)T (xi − µM L)
N i=1
Machine Learning 30

32. The GMM assumption
• There are k components: {ci}k
i=1
• Component ci has an associated mean
vector µi
µ2
•
µ1
µ3
•
Machine Learning 31

33. The GMM assumption
• There are k components: {ci}k
i=1
• Component ci has an associated mean
vector µi
µ2
• Each component generates data from a
Gaussian with mean µi and covariance µ1
matrix Σi
• Each sample is generated according to µ3
the following guidelines:
Machine Learning 32

34. The GMM assumption
• There are k components: {ci}k
i=1
• Component ci has an associated mean
vector µi
• Each component generates data from a µ2
Gaussian with mean µi and covariance
matrix Σi
• Each sample is generated according to
the following guidelines:
– Randomly select component ci
with probability P (ci) = wi, s.t.
∑k
i=1 wi = 1
Machine Learning 33

35. The GMM assumption
• There are k components: {ci}k
i=1
• Component ci has an associated mean
vector µi
µ2
• Each component generates data from a
x
Gaussian with mean µi and covariance
matrix Σi
• Each sample is generated according to
the following guidelines:
– Randomly select component ci with
probability P (ci) = wi, s.t.
∑k
i=1 wi = 1
– Sample ~ N (µi, Σi)
Machine Learning 34

36. Probability density function of GMM
“Linear combination” of Gaussians:
k
∑ k
∑
f (x) = wiN (x; µi, Σi) , where wi = 1
i=1 i=1
0.018
0.016
0.014
0.012
0.01
f (x)
0.008
2
2
w1 N µ1 , σ1 w2 N µ2 , σ2
0.006
2
w3 N µ3 , σ3
0.004
0.002
0
0 50 100 150 200 250
(a) The pdf of an 1D GMM with 3 components. (b) The pdf of an 2D GMM with 3 components.
Figure 2: Probability density function of some GMMs.
Machine Learning 35

37. GMM: Problem definition
k
∑ k
∑
f (x) = wiN (x; µi, Σi) , where wi = 1
i=1 i=1
Given a training set, how to model these data point using GMM?
• Given:
– The trainning set: {xi}N
i=1
– Number of clusters: k
• Goal: model this data using a mixture of Gaussians
– Weights: w1, w2, ..., wk
– Means and covariances: µ1, µ2, ..., µk ; Σ1, Σ2, ..., Σk
Machine Learning 36

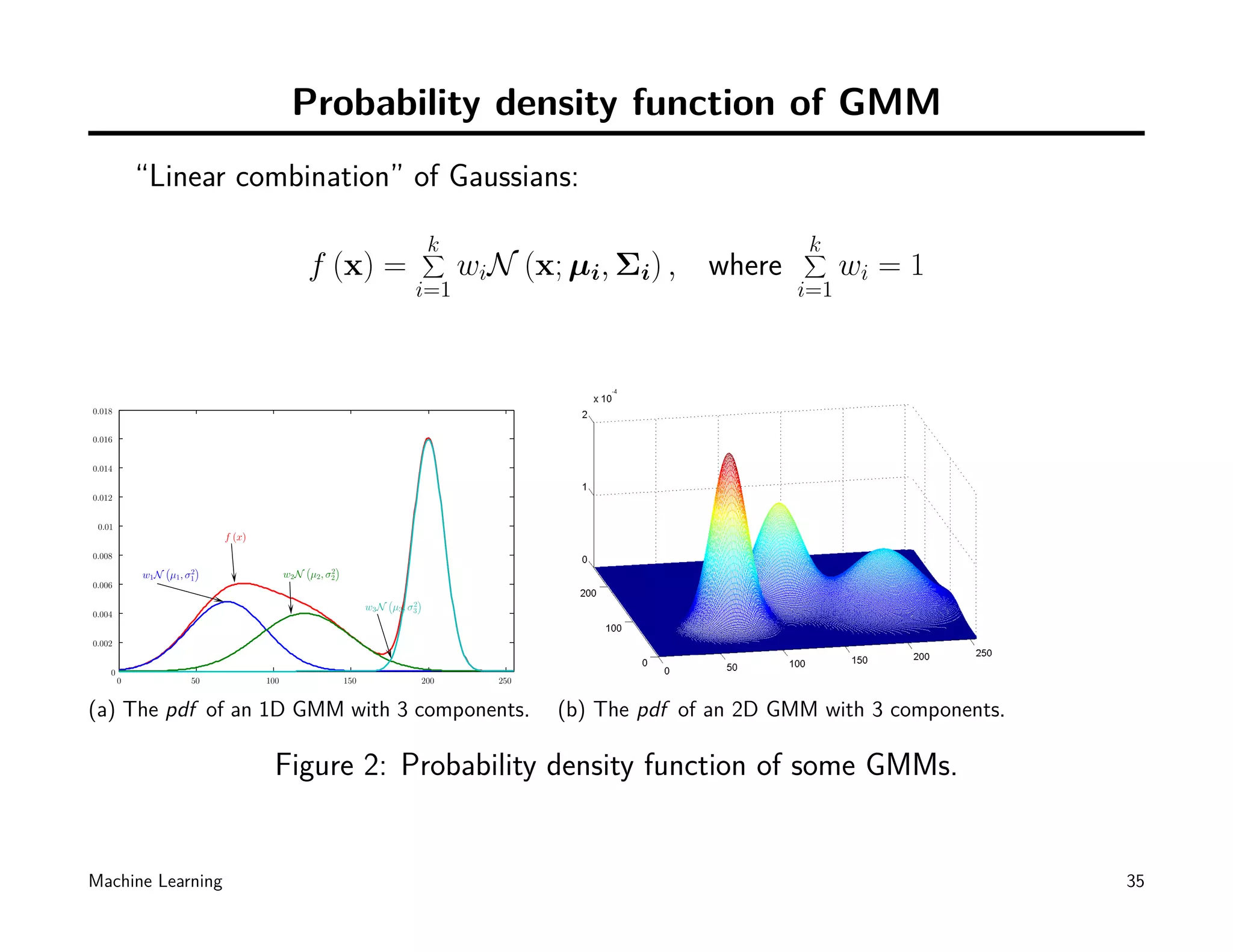
38. Computing likelihoods in unsupervised case
k
∑ k
∑
f (x) = wiN (x; µi, Σi) , where wi = 1
i=1 i=1
• Given a mixture of Gaussians, denoted by G. For any x, we can define the
likelihood:
P (x | G) = P (x | w1, µ1, Σ1, ..., wk , µk , Σk )
k
∑
= P (x | ci) P (ci)
i=1
k
∑
= wiN (x; µi, Σi)
i=1
• So we can define likelihood for the whole training set [Why?]
N
∏
P (x1, x2, ..., xN | G) = P (xi | G)
i=1
N ∑
∏ k
= wj N (xi; µj , Σj )
i=1 j=1
Machine Learning 37

39. Estimating GMM parameters
• We known this: Maximum Likelihood Estimation
 
N
∑ k
∑
ln P (X | G) = ln 
 wj N (xi; µj , Σj )

i=1 j=1
– For the max likelihood:
∂ ln P (X | G)
0=
∂µj
– This leads to non-linear non-analytically-solvable equations!
• Use gradient descent
– Slow but doable
• A much cuter and recently popular method...
Machine Learning 38

40. E.M. for GMM
• Remember:
– We have the training set {xi}N , the number of components k.
i=1
– Assume we know p (c1) = w1, p (c2) = w2, ..., p (ck ) = wk
– We don’t know µ1, µ2, ..., µk
The likelihood:
p (data | µ1, µ2, ..., µk ) = p (x1, x2, ..., xN | µ1, µ2, ..., µk )
N
∏
= p (xi | µ1, µ2, ..., µk )
i=1
N ∑
∏ k
= p (xi | wj , µ1, µ2, ..., µk ) p (cj )
i=1 j=1  
N ∑
∏ k 1 ( )
2
= K exp − 2 xi − µj wi

i=1 j=1 2σ
Machine Learning 39

41. E.M. for GMM
• For Max. Likelihood, we know ∂µ log p (data | µ1, µ2, ..., µk ) = 0
∂
i
• Some wild algebra turns this into: For Maximum Likelihood, for each j:
N
∑
p (cj | xi, µ1, µ2, ..., µk ) xi
i=1
µj = N
∑
p (cj | xi, µ1, µ2, ..., µk )
i=1
This is N non-linear equations of µj ’s.
• So:
– If, for each xi, we know p (cj | xi, µ1, µ2, ..., µk ), then we could easily compute
µj ,
– If we know each µj , we could compute p (cj | xi, µ1, µ2, ..., µk ) for each xi
and cj .
Machine Learning 40

42. E.M. for GMM
• E.M. is coming: on the t’th iteration, let our estimates be
λt = {µ1 (t) , µ2 (t) , ..., µk (t)}
• E-step: compute the expected classes of all data points for each class
( )
p (xi | cj , λt) p (cj | λt) p xi | cj , µj (t) , σj I p (cj )
p (cj | xi, λt) = =
p (xi | λt) k
∑
p (xi | cm, µm (t) , σmI) p (cm)
m=1
• M-step: compute µ given our data’s class membership distributions
N
∑
p (cj | xi, λt) xi
i=1
µj (t + 1) = N
∑
p (cj | xi, λt)
i=1
Machine Learning 41

43. E.M. for General GMM: E-step
• On the t’th iteration, let our estimates be
λt = {µ1 (t) , µ2 (t) , ..., µk (t) , Σ1 (t) , Σ2 (t) , ..., Σk (t) , w1 (t) , w2 (t) , ..., wk (t)}
• E-step: compute the expected classes of all data points for each class
p (xi | cj , λt) p (cj | λt)
τij (t) ≡ p (cj | xi, λt) =
p (xi | λt)
( )
p xi | cj , µj (t) , Σj (t) wj (t)
= k
∑
p (xi | cm, µm (t) , Σj (t)) wm (t)
m=1
Machine Learning 42

44. E.M. for General GMM: M-step
• M-step: compute µ given our data’s class membership distributions
N
∑ N
∑
p (cj | xi, λt) p (cj | xi, λt) xi
i=1 i=1
wj (t + 1) = µj (t + 1) = N
N ∑
p (cj | xi, λt)
i=1
1 N
∑ 1 N
∑
= τij (t) = τij (t) xi
N i=1 N wj (t + 1) i=1
N
∑ [ ][ ]
T
p (cj | xi, λt) xi − µj (t + 1) xi − µj (t + 1)
i=1
Σj (t + 1) = N
∑
p (cj | xi, λt)
i=1
1 N
∑ [ ][ ]
T
= τij (t) xi − µj (t + 1) xi − µj (t + 1)
N wj (t + 1) i=1
Machine Learning 43

45. E.M. for General GMM: Initialization
• wj = 1/k, j = 1, 2, ..., k
• Each µj is set to a randomly selected point
– Or use K-means for this initialization.
• Each Σj is computed using the equation in previous slide...
Machine Learning 44

46. Regularized E.M. for GMM
• In case of REM, the entropy H (·) is
N
∑ k
∑
H (C | X; λt) =− p (cj | xi; λt) log p (cj | xi; λt)
i=1 i=1
N
∑ k
∑
=− τij (t) log τij (t)
i=1 i=1
and the likelihood will be
L (λt; X, C) =L (λt; X, C) − γH (C | X; λt)
N
∑ k
∑
= log wj p (xi | cj , λt)
i=1 j=1
N
∑ k
∑
+γ τij (t) log τij (t)
i=1 i=1
Machine Learning 45

47. Regularized E.M. for GMM
• Some algebra [5] turns into:
N
∑
p (cj | xi, λt) (1 + γ log p (cj | xi, λt))
i=1
wj (t + 1) =
N
1 N
∑
= τij (t) (1 + γ log τij (t))
N i=1
N
∑
p (cj | xi, λt) xi (1 + γ log p (cj | xi, λt))
µj (t + 1) = i=1
N
∑
p (cj | xi, λt) (1 + γ log p (cj | xi, λt))
i=1
1 N
∑
= τij (t) xi (1 + γ log τij (t))
N wj (t + 1) i=1
Machine Learning 46

48. Regularized E.M. for GMM
• Some algebra [5] turns into (cont.):
1 N
∑
Σj (t + 1) = τij (t) (1 + γ log τij (t)) dij (t + 1)
N wj (t + 1) i=1
where [ ][ ]
T
dij (t + 1) = xi − µj (t + 1) xi − µj (t + 1)
Machine Learning 47

49. Demonstration
• EM for GMM
• REM for GMM
Machine Learning 48

50. Local optimum solution
• E.M. is guaranteed to find the local optimal solution by monotonically increasing
the log-likelihood
• Whether it converges to the global optimal solution depends on the initialization
18 15
16
14
12 10
10
8
6 5
4
2
0 0
−10 −5 0 5 10 15 −10 −5 0 5 10 15
Machine Learning 49

51. GMM: Selecting the number of components
• We can run the E.M. algorithm with different numbers of components.
– Need a criteria for selecting the “best” number of components
15 16 16
14 14
12 12
10
10 10
8 8
6 6
5
4 4
2 2
0 0 0
−10 −5 0 5 10 15 −10 −5 0 5 10 15 −10 −5 0 5 10 15
Machine Learning 50

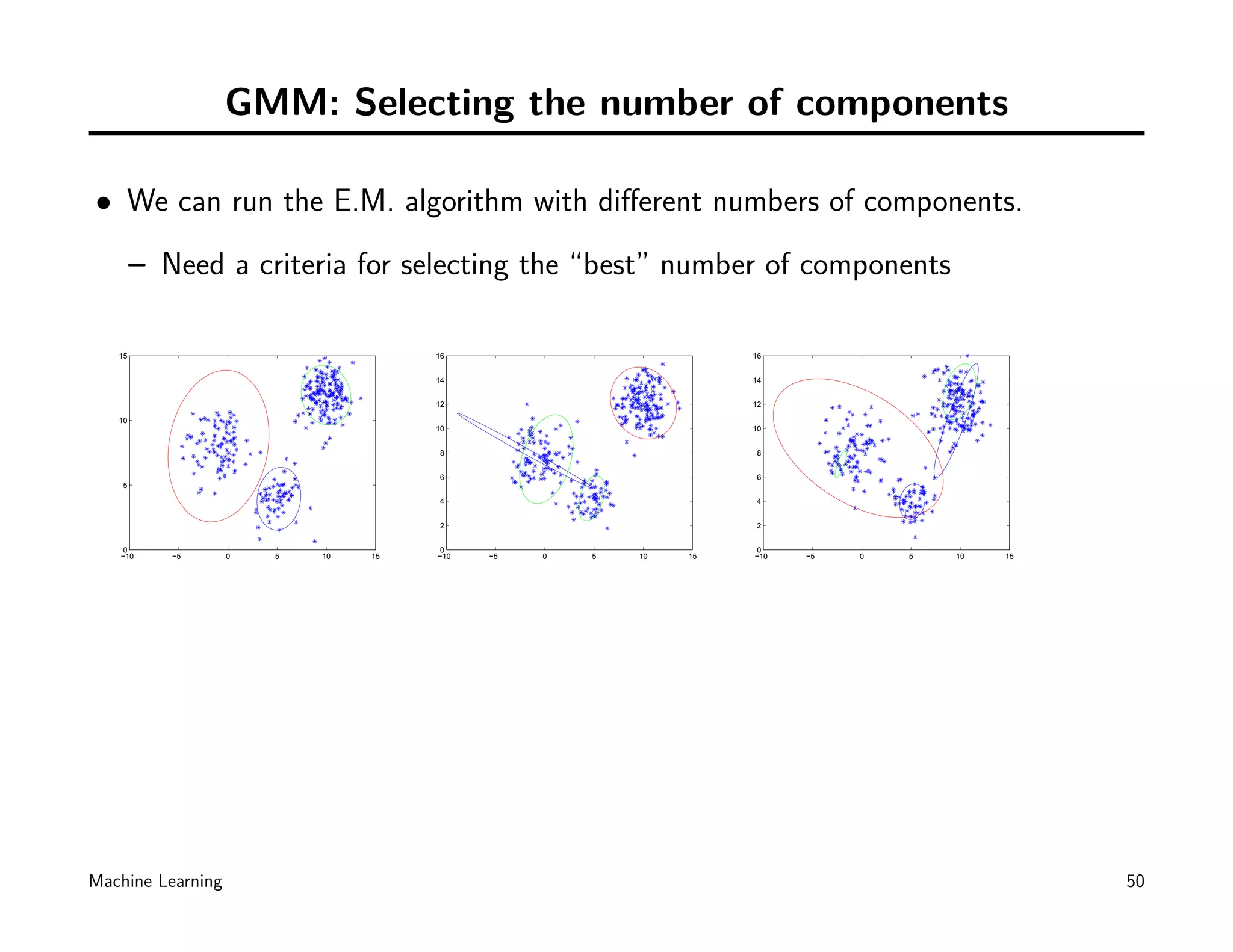
52. GMM: Model Selection
• Empirically/Experimentally [Sure!]
• Cross-Validation [How?]
• BIC
• ...
Machine Learning 51

53. GMM: Model Selection
• Empirically/Experimentally
– Typically 3-5 components
• Cross-Validation: K-fold, leave-one-out...
– Omit each point xi in turn, estimate the parameters θ −i on the basis of the
remaining points, then evaluate
N ( )
∑ −i
log p xi | θ
i=1
• BIC: find k (the number of components) that minimize the BIC
( ) dk
BIC = − log p data | θm + log n
2
where dk is the number of (effective) parameters in the k-component mixture.
Machine Learning 52

54. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 53

55. Gaussian mixtures for classification
p (x | y = i) p (y = i)
p (y = i | x) =
p (x)
• To build a Bayesian classifier based on GMM, we can use GMM to model data in
each class
– So each class is modeled by one k-component GMM.
• For example:
Class 0: p (y = 0) , p (x | θ 0), (a 3-component mixture)
Class 1: p (y = 1) , p (x | θ 1), (a 3-component mixture)
Class 2: p (y = 2) , p (x | θ 2), (a 3-component mixture)
...
Machine Learning 54

56. GMM for Classification
• As previous, each class is modeled by a k-component GMM.
• A new test sample x is classified according to
c = arg max p (y = i) p (x | θ i)
i
where
k
∑
p (x | θ i) = wiN (x; µi, Σi)
i=1
• Simple, quick (and is actually used!)
Machine Learning 55

57. Contents
• Unsupervised Learning
• K-means clustering
• Expectation Maximization (E.M.)
– Regularized EM
– Model Selection
• Gaussian mixtures as a Density Estimator
– Gaussian mixtures
– EM for mixtures
• Gaussian mixtures for classification
• Case studies
Machine Learning 56

58. Case studies
• Background subtraction
– GMM for each pixel
• Speech recognition
– GMM for the underlying distribution of feature vectors of each phone
• Many, many others...
Machine Learning 57

59. What you should already know?
• K-means as a trivial classifier
• E.M. - an algorithm for solving many MLE problems
• GMM - a tool for modeling data
– Note 1: We can have a mixture model of many different types of distribution,
not only Gaussians
– Note 2: Compute the sum of Gaussians may be expensive, some approximations
are available [3]
• Model selection:
– Bayesian Information Criterion
Machine Learning 58

60. Q&A
Machine Learning 59

61. References
[1] N. Laird A. Dempster and D. Rubin. Maximum likelihood from incomplete data
via the em algorithm. Journal of the Royal Statistical Society. Series B (Method-
ological), 39(1):pp. 1–38., 1977.
[2] David Arthur and Sergei Vassilvitskii. k-means ++ : The Advantages of Careful
Seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on
Discrete algorithms, volume 8, pages 1027–1035, 2007.
[3] N. Gumerov C. Yang, R. Duraiswami and L. Davis. Improved fast gauss transform
and efficient kernel density estimation. In IEEE International Conference on
Computer Vision, pages pages 464–471, 2003.
[4] Charles Elkan. Using the Triangle Inequality to Accelerate k-Means. In Proceed-
Machine Learning 60

62. ings of the Twentieth International Conference on Machine Learning (ICML),
2003.
[5] Keshu Zhang Haifeng Li and Tao Jiang. The regularized em algorithm. In
Proceedings of the 20th National Conference on Artificial Intelligence, pages
pages 807 – 812, Pittsburgh, PA, 2005.
[6] Greg Hamerly and Charles Elkan. Learning the k in k-means. In In Neural
Information Processing Systems. MIT Press, 2003.
[7] Tapas Kanungo, David M Mount, Nathan S Netanyahu, Christine D Piatko, Ruth
Silverman, and Angela Y Wu. An efficient k-means clustering algorithm: anal-
ysis and implementation. IEEE Transactions on Pattern Analysis and Machine
Intelligence, 24(7):881–892, July 2002.
[8] J MacQueen. Some methods for classification and analysis of multivariate obser-
vations. In Proceedings of 5th Berkeley Symposium on Mathematical Statistics
and Probability, volume 233, pages 281–297. University of California Press, 1967.
Machine Learning 61

63. [9] C.F. Wu. On the convergence properties of the em algorithm. The Annals of
Statistics, 11:95–103, 1983.
Machine Learning 62