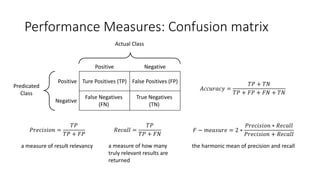
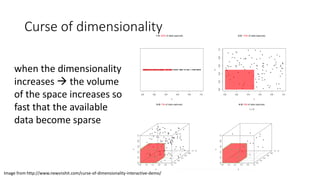
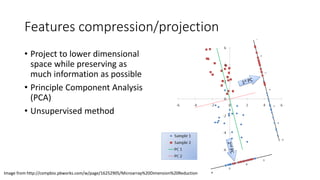
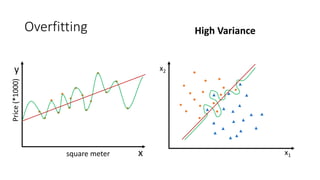
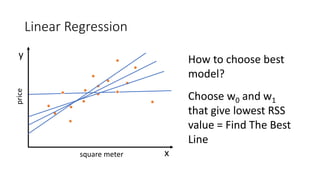
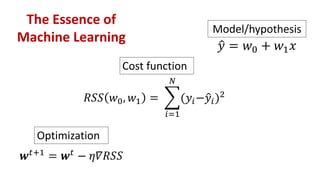
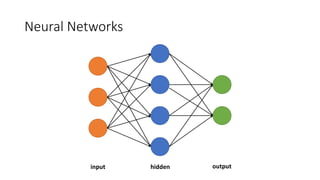
This document provides an overview of regression analysis and linear regression. It explains that regression analysis estimates relationships among variables to predict continuous outcomes. Linear regression finds the best fitting line through minimizing error. It describes modeling with multiple features, representing data in vector and matrix form, and using gradient descent optimization to learn the weights through iterative updates. The goal is to minimize a cost function measuring error between predictions and true values.

1. www.qunaieer.com
‫ﺗﻨﻈﯿﻢ‬

2. ‫اﻟﻤﺤﺎﺿﺮة‬ ‫طﺮﯾﻘﺔ‬
•‫اﻷﺳﺎﺳﯾﺔ‬ ‫واﻟﻣﻔﺎھﯾم‬ ‫اﻟﻣﺻطﻠﺣﺎت‬ ‫ﺷرح‬
•‫ﺑﺎﻟﻌرﺑﻲ‬ ‫واﻟﺷرح‬ ‫ﺑﺎﻹﻧﺟﻠﯾزي‬ ‫اﻟﻌرض‬ ‫ﺷراﺋﺢ‬ ‫وأﻏﻠب‬ ‫اﻟﻣﺻطﻠﺣﺎت‬
•‫ﻟﻸﺳﺎﺳﯾﺎت‬ ‫ﻣﻔﺻل‬ ‫ﺷرح‬
•‫اﻟﺷﮭﯾرة‬ ‫ﻟﻠﺧوارزﻣﯾﺎت‬ ‫ﺳرﯾﻌﺔ‬ ‫إﺷﺎرات‬
•‫ﺑﺳﯾطﺔ‬ ‫ﻋﻣﻠﯾﺔ‬ ‫أﻣﺛﻠﺔ‬
•‫ﻣﻘﺗرﺣﺔ‬ ‫ﺗﻌﻠم‬ ‫ﺧطﺔ‬

3. ‫اﻵﻟﺔ؟‬ ‫ﺗﻌﻠﻢ‬ ‫ھﻮ‬ ‫ﻣﺎ‬
•‫ﺑﺎﻟﺗﻔﺻﯾل‬ ‫ﺑرﻣﺟﺗﮫ‬ ‫ﻣن‬ ً‫ﻻ‬‫ﺑد‬ ‫ﻧﻔﺳﮫ‬ ‫ﻣن‬ ‫اﻟﺗﻌﻠم‬ ‫اﻟﺣﺎﺳب‬ ‫ﯾﻣﻛن‬ ‫ﻋﻠم‬ ‫ھو‬
•‫ﻧﻣﺎذج‬ ‫ﺑﻧﺎء‬ ‫طرﯾﻖ‬ ‫ﻋن‬ ‫اﻟﺑﯾﺎﻧﺎت‬ ‫ﺟوھر‬ ‫اﺧﺗزال‬)models(‫واﻟﺗوﻗﻌﺎت‬ ‫اﻟﻘرارات‬ ‫واﺗﺧﺎذ‬ ،
‫ﻋﻠﯾﮭﺎ‬ ً‫ء‬‫ﺑﻧﺎ‬ ‫اﻟﻣﺳﺗﻘﺑﻠﯾﺔ‬

5. Regression

6. •Regression analysis is a statistical
process for estimating the relationships
among variables
•Used to predict continuous outcomes

7. Regression Examples

8. Linear Regression
Line Equation
𝑦𝑦 = 𝑏𝑏 + 𝑎𝑎𝑎𝑎
�𝑦𝑦 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥
intercept slope
x
y
square meter
price
Model/hypothesis

9. Linear Regression
x
y �𝑦𝑦 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥
square meter
Price(*1000)
example
𝑤𝑤0=50, 𝑤𝑤1=1.8,
x=500
�𝑦𝑦 = 950

10. Linear Regression
x
y How to quantify
error?
square meter
price

11. Linear Regression
𝑅𝑅𝑅𝑅𝑅𝑅 𝑤𝑤0, 𝑤𝑤1 = �
𝑖𝑖=1
𝑁𝑁
(�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖)2
Residual Sum of Squares (RSS)
Where �𝑦𝑦𝑖𝑖 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥𝑖𝑖
Cost function

12. Linear Regression
How to choose best
model?
Choose w0 and w1
that give lowest RSS
value = Find The Best
Line
x
y
square meter
price

13. Optimization
Image from https://ccse.lbl.gov/Research/Optimization/index.html

14. Optimization (convex)
derivative = 0
derivative > 0derivative < 0
The gradient points in the direction
of the greatest rate of increase of
the function, and its magnitude is
the slope of the graph in that
direction. - Wikipedia

15. Optimization (convex)
Image from http://codingwiththomas.blogspot.com/2012/09/particle-swarm-optimization.html
𝑅𝑅𝑅𝑅𝑅𝑅
𝑤𝑤0
𝑤𝑤1

16. Optimization (convex)
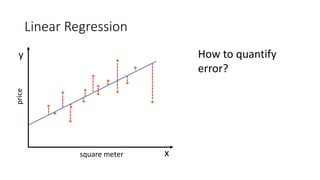
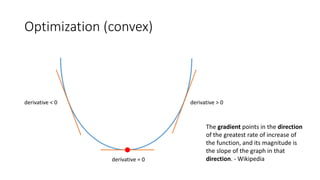
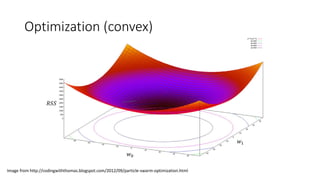
• First, lets compute the gradient of our cost function
• To find best lines, there are two ways:
• Analytical (normal equation)
• Iterative (gradient descent)
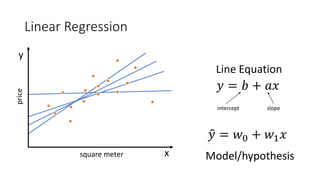
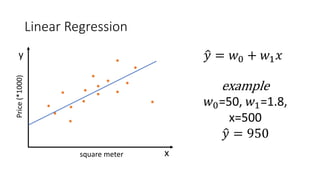
Where �𝑦𝑦𝑖𝑖 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥𝑖𝑖
𝛻𝛻𝑅𝑅𝑅𝑅𝑅𝑅(𝑤𝑤0, 𝑤𝑤1) =
−2 ∑𝑖𝑖=1
𝑁𝑁
[�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖]
−2 ∑𝑖𝑖=1
𝑁𝑁
[�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖]𝑥𝑥𝑖𝑖

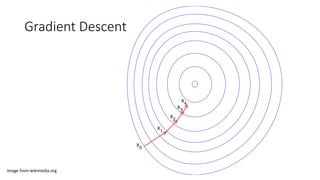
17. Gradient Descent
𝒘𝒘𝑡𝑡+1
= 𝒘𝒘𝑡𝑡
− 𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂
𝑤𝑤0
𝑡𝑡+1
𝑤𝑤1
𝑡𝑡+1 =
𝑤𝑤0
𝑡𝑡
𝑤𝑤1
𝑡𝑡 − 𝜂𝜂
−2 ∑𝑖𝑖=1
𝑁𝑁
[�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖]
−2 ∑𝑖𝑖=1
𝑁𝑁
[�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖]𝑥𝑥𝑖𝑖
Update the weights to minimize the cost function
𝜂𝜂 is the step size (important hyper-parameter)

18. Gradient Descent
Image from wikimedia.org

19. Linear Regression: Algorithm
• Objective: min
𝑤𝑤0,𝑤𝑤1
𝐽𝐽(𝑤𝑤0, 𝑤𝑤1) , here 𝐽𝐽 𝑤𝑤0, 𝑤𝑤1 = 𝑅𝑅𝑅𝑅𝑅𝑅(𝑤𝑤0, 𝑤𝑤1)
• Initialize 𝑤𝑤0, 𝑤𝑤1, e.g. random numbers or zeros
• 𝑓𝑓𝑓𝑓𝑓𝑓 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 𝑜𝑜𝑜𝑜 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐:
• Compute the gradient: 𝛻𝛻𝐽𝐽
• 𝑊𝑊𝑡𝑡+1
= 𝑊𝑊𝑡𝑡
− 𝜂𝜂𝜂𝜂𝐽𝐽, where W = 𝑤𝑤0
𝑤𝑤1

20. Model/hypothesis
Cost function
Optimization
�𝑦𝑦 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥
𝑅𝑅𝑅𝑅𝑅𝑅 𝑤𝑤0, 𝑤𝑤1 = �
𝑖𝑖=1
𝑁𝑁
(𝑦𝑦𝑖𝑖−�𝑦𝑦𝑖𝑖)2
𝒘𝒘𝑡𝑡+1
= 𝒘𝒘𝑡𝑡
− 𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂𝜂
The Essence of
Machine Learning

21. Linear Regression: Multiple features
• Example: for house pricing, in addition to size in square meters, we
can use city, location, number of rooms, number of bathrooms, etc
• The model/hypothesis becomes
�𝑦𝑦 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥 1 + 𝑤𝑤2 𝑥𝑥2 + ⋯ + 𝑤𝑤𝑛𝑛 𝑥𝑥𝑛𝑛
𝑤𝑤𝑒𝑒ℎ𝑟𝑟𝑟𝑟 𝑛𝑛 = 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓

22. Representation
• Vector representation of 𝑛𝑛 features
�𝑦𝑦 = 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥 1 + 𝑤𝑤2 𝑥𝑥2 + ⋯ + 𝑤𝑤𝑛𝑛 𝑥𝑥𝑛𝑛
𝒙𝒙 =
𝑥𝑥0 = 1
𝑥𝑥1
𝑥𝑥2
⋮
𝑥𝑥𝑛𝑛
𝒘𝒘 =
𝑤𝑤0
𝑤𝑤1
𝑤𝑤2
⋮
𝑤𝑤𝑛𝑛
�𝑦𝑦 = 𝒘𝒘 𝑇𝑇
𝒙𝒙
�𝑦𝑦 = 𝑤𝑤0 𝑤𝑤1 𝑤𝑤2 ⋯ 𝑤𝑤𝑛𝑛
𝑥𝑥0
𝑥𝑥1
𝑥𝑥2
⋮
𝑥𝑥𝑛𝑛

23. Representation
• matrix representation of 𝑚𝑚 data samples and 𝑛𝑛 features
�𝑦𝑦(𝑖𝑖)
= 𝑤𝑤0 + 𝑤𝑤1 𝑥𝑥1
(𝑖𝑖)
+ 𝑤𝑤2 𝑥𝑥2
(𝑖𝑖)
+ ⋯ + 𝑤𝑤𝑛𝑛 𝑥𝑥𝑛𝑛
(𝑖𝑖)
𝑋𝑋 =
𝑥𝑥0
(0)
𝑥𝑥1
(0)
⋯ 𝑥𝑥𝑛𝑛
(0)
𝑥𝑥0
(1)
𝑥𝑥1
(1)
⋯ 𝑥𝑥𝑛𝑛
(1)
⋮
𝑥𝑥0
(𝑚𝑚)
⋮
𝑥𝑥1
(𝑚𝑚)
⋱
…
⋮
𝑥𝑥𝑛𝑛
(𝑚𝑚)
𝒘𝒘 =
𝑤𝑤0
𝑤𝑤1
𝑤𝑤2
⋮
𝑤𝑤𝑛𝑛
�𝒚𝒚 = 𝑋𝑋𝒘𝒘
𝑖𝑖 is the 𝑖𝑖th data sample
Size: m x n Size: n x 1
�𝑦𝑦(0)
�𝑦𝑦(1)
�𝑦𝑦(2)
⋮
�𝑦𝑦(𝑚𝑚)
=
𝑥𝑥0
(0)
𝑥𝑥1
(0)
⋯ 𝑥𝑥𝑛𝑛
(0)
𝑥𝑥0
(1)
𝑥𝑥1
(1)
⋯ 𝑥𝑥𝑛𝑛
(1)
⋮
𝑥𝑥0
(𝑚𝑚)
⋮
𝑥𝑥1
(𝑚𝑚)
⋱
…
⋮
𝑥𝑥𝑛𝑛
(𝑚𝑚)
×
𝑤𝑤0
𝑤𝑤1
𝑤𝑤2
⋮
𝑤𝑤𝑛𝑛

24. Analytical solution (normal equation)
𝒘𝒘 = (𝑋𝑋 𝑇𝑇
𝑋𝑋)−1
𝑋𝑋 𝑇𝑇
𝒚𝒚

25. Analytical vs. Gradient Descent
• Gradient descent: must select parameter 𝜂𝜂
• Analytical solution: no parameter selection
• Gradient descent: a lot of iterations
• Analytical solution: no need for iterations
• Gradient descent: works with large number of features
• Analytical solution: slow with large number of features

26. Demo
• Matrices operations
• Simple linear regression implementation
• Scikit-learn library’s linear regression

27. Classification

28. classification
x1
x2

29. Classification Examples

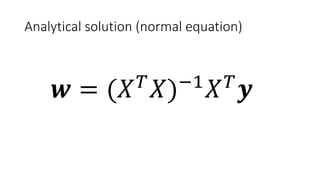
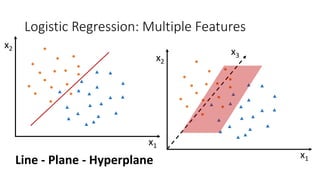
30. Logistic Regression
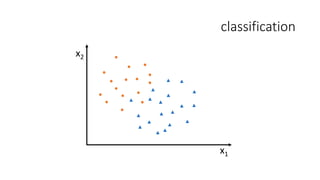
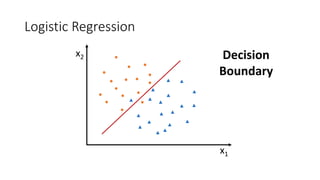
• How to turn regression problem into classification one?
• y = 0 or 1
• Map values to [0 1] range
𝑔𝑔 𝑥𝑥 =
1
1 + 𝑒𝑒−𝑥𝑥
Sigmoid/Logistic Function

31. Logistic Regression
• Model (sigmoidlogistic function)
• Interpretation (probability)
ℎ𝒘𝒘 𝒙𝒙 = 𝑔𝑔 𝒘𝒘𝑇𝑇
𝒙𝒙 =
1
1 + 𝑒𝑒−𝒘𝒘𝑇𝑇 𝒙𝒙
ℎ𝒘𝒘 𝒙𝒙 = 𝑝𝑝 𝑦𝑦 = 1|𝒙𝒙; 𝒘𝒘
𝑖𝑖𝑖𝑖 ℎ𝒘𝒘 𝒙𝒙 ≥ 0.5 ⇒ 𝑦𝑦 = 1
𝑖𝑖𝑖𝑖ℎ𝒘𝒘 𝒙𝒙 < 0.5 ⇒ 𝑦𝑦 = 0

32. Logistic Regression
x1
x2 Decision
Boundary

33. Logistic Regression
• Cost function
𝐽𝐽 𝒘𝒘 = 𝑦𝑦 log(ℎ𝒘𝒘 𝒙𝒙 ) + 1 − 𝑦𝑦 log(1 − ℎ𝒘𝒘(𝒙𝒙))
ℎ𝒘𝒘 𝒙𝒙 = 𝑔𝑔 𝒘𝒘𝑇𝑇
𝒙𝒙 =
1
1 + 𝑒𝑒−𝒘𝒘𝑇𝑇 𝒙𝒙

34. Logistic Regression
•Optimization: Gradient Descent
•Exactly like linear regression
•Find best w parameters that minimize the cost
function

35. Logistic Regression: Algorithm
• Objective: min
𝑤𝑤0,𝑤𝑤1
𝐽𝐽(𝑤𝑤0, 𝑤𝑤1) , here 𝐽𝐽 𝑤𝑤0, 𝑤𝑤1 is the logistic regression
cost function
• Initialize 𝑤𝑤0, 𝑤𝑤1, e.g. random numbers or zeros
• 𝑓𝑓𝑓𝑓𝑓𝑓 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 𝑜𝑜𝑜𝑜 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐:
• Compute the gradient: 𝛻𝛻𝐽𝐽 (not discussed here)
• 𝒘𝒘𝑡𝑡+1 = 𝒘𝒘𝑡𝑡 − 𝜂𝜂𝜂𝜂𝐽𝐽, where 𝐰𝐰 = 𝑤𝑤0
𝑤𝑤1

36. Logistic Regression
• Multi-class classification

37. Logistic Regression
One-vs-All

38. Logistic Regression: Multiple Features
x1
x2
x1
x2
x3
Line - Plane - Hyperplane

39. Demo
• Scikit-learn library’s logistic regression

40. Other Classification Algorithms

41. Neural Networks
input hidden output

42. Support Victor Machines (SVM)
x1
x2

43. Decision Trees
Credit?
Term? Incom?
Term?
Safe
SafeRisky
SafeRisky
Risky
excellent poor
fair
3 year 5 year high low
3 year 5 year

44. K Nearest Neighbors (KNN)
x1
x2
?
5 Nearest Neighbors

45. Clustering

46. Clustering
•Unsupervised learning
•Group similar items into clusters
•K-Mean algorithm

47. Clustering Examples

48. K-Mean
x1
x2

49. K-Mean
x1
x2

50. K-Mean
x1
x2

51. K-Mean
x1
x2

52. K-Mean
x1
x2

53. K-Mean
x1
x2

54. K-Mean
x1
x2

55. K-Mean
x1
x2

56. K-Mean
x1
x2

57. K-Mean Algorithm
• Select number of clusters: 𝐾𝐾 (number of centroids 𝜇𝜇1, … , 𝜇𝜇𝐾𝐾)
• Given dataset of size N
• 𝑓𝑓𝑜𝑜𝑜𝑜 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 𝑡𝑡:
• 𝑓𝑓𝑓𝑓𝑓𝑓 𝑖𝑖 = 1 𝑡𝑡𝑡𝑡 𝑁𝑁:
• 𝑐𝑐𝑖𝑖 ≔ assign cluster 𝑐𝑐𝑖𝑖 to sample 𝑥𝑥𝑖𝑖 as the smallest Euclidean distance
between 𝑥𝑥𝑖𝑖 and the centroids
• 𝑓𝑓𝑜𝑜𝑜𝑜 𝑘𝑘 = 1 𝑡𝑡𝑡𝑡 𝐾𝐾:
• 𝜇𝜇𝑘𝑘 ≔ mean of the points assigned to cluster 𝑐𝑐𝑘𝑘

58. Demo
• Scikit-learn library’s k-mean

59. Machine Learning
Supervised Unsupervised
ClassificationRegression Clustering

60. Other Machine Learning Algorithms
•Probabilistic models
•Ensemble methods
•Reinforcement Learning
•Recommendation algorithms (e.g., Matrix
Factorization)
•Deep Learning

61. Linear vs Non-linear
x1
x2
x
y
square meter
price
Multi-layer Neural Networks
Support Victor Machines (kernel trick)

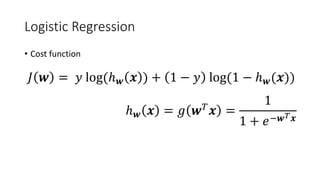
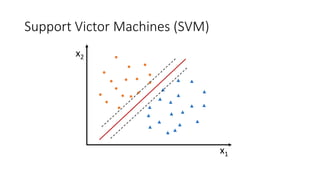
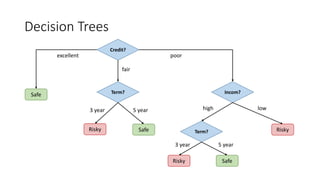
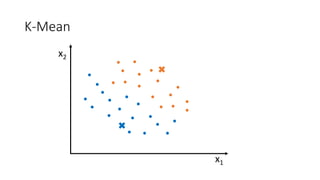
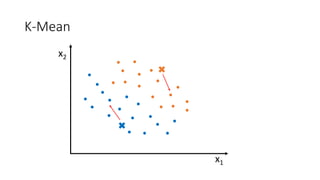
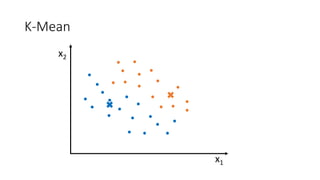
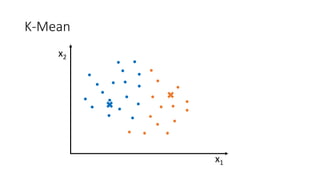
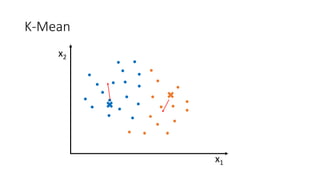
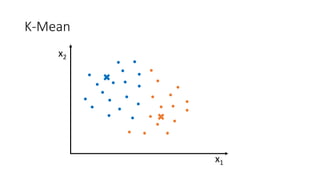
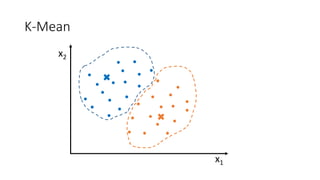
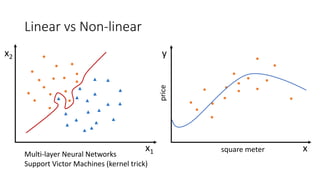
62. Kernel Trick 𝐾𝐾 𝑥𝑥1, 𝑥𝑥2 = [𝑥𝑥1, 𝑥𝑥2, 𝑥𝑥1
2
+ 𝑥𝑥2
2
]
Image from http://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html

63. Practical aspects

64. Data Preprocessing
• Missing data
• Elimination (samples/features)
• Imputation
• Categorical data
• Mapping (for ordinal features)
• One-hot-encoding (for nominal features)
• Features scaling (normalization, standardization)
• Data/problem specific preprocessing (e.g., images, signals, text)
𝑥𝑥𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛
(𝑖𝑖)
=
𝑥𝑥(𝑖𝑖) − 𝑥𝑥 𝑚𝑚𝑚𝑚𝑚𝑚
𝑥𝑥 𝑚𝑚𝑚𝑚𝑚𝑚 − 𝑥𝑥 𝑚𝑚𝑚𝑚𝑚𝑚
𝑥𝑥𝑠𝑠𝑠𝑠𝑠𝑠
(𝑖𝑖)
=
𝑥𝑥(𝑖𝑖) − 𝜇𝜇𝑥𝑥
𝜎𝜎𝑥𝑥
,
𝑤𝑤ℎ𝑒𝑒𝑒𝑒𝑒𝑒 𝜇𝜇𝑥𝑥: 𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 𝑜𝑜𝑜𝑜 𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓 𝑥𝑥, 𝜎𝜎𝑥𝑥: 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑

65. Model Evaluation
• Splitting data (training, validation, testing) IMPORTANT
• No hard rule: usually 60%-20%-20% will be fine
• k-fold cross-validation
• If dataset is very small
• Leave-one-out
• Fine-tuning hyper-parameters
• Automated hyper-parameter selection
• Using validation set
Training Validation Testing

66. Performance Measures
• Depending on the problem
• Some of the well-known measure are:
• Classification measures
• Accuracy
• Confusion matrix and related measures
• Regression
• Mean Squared Error
• R2 metric
• Clustering performance measure is not straight forward, and will not
be discussed here

67. Performance Measures: Accuracy
• If we have 100 persons, one of them having cancer. What is the accuracy if
classify all of them as having no cancer?
• Accuracy is not good for heavily biased class distribution
𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 =
𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝
𝑎𝑎𝑎𝑎𝑎𝑎 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝

68. Performance Measures: Confusion matrix
NegativePositive
False Positives (FP)Ture Positives (TP)Positive
True Negatives
(TN)
False Negatives
(FN)
Negative
Predicated
Class
Actual Class
𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 =
𝑇𝑇𝑇𝑇 + 𝑇𝑇𝑇𝑇
𝑇𝑇𝑇𝑇 + 𝐹𝐹𝐹𝐹 + 𝐹𝐹𝐹𝐹 + 𝑇𝑇𝑇𝑇
𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 =
𝑇𝑇𝑇𝑇
𝑇𝑇𝑇𝑇 + 𝐹𝐹𝐹𝐹
𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅 =
𝑇𝑇𝑇𝑇
𝑇𝑇𝑇𝑇 + 𝐹𝐹𝐹𝐹
𝐹𝐹 − 𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 = 2 ∗
𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 ∗ 𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 + 𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
a measure of result relevancy a measure of how many
truly relevant results are
returned
the harmonic mean of precision and recall

69. Performance Measures: Mean Squared Error (MSE)
• Defined as
• Gives an idea of how wrong the predictions were
• Only gives an idea of the magnitude of the error, but not the direction (e.g. over
or under predicting)
• Root Mean Squared Error (RMSE) is the square root of MSE, which has the same
unit of the data
𝑀𝑀𝑀𝑀𝑀𝑀 =
1
𝑛𝑛
�
𝑖𝑖=1
𝑛𝑛
(�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖)2

70. Performance Measures: R2
• Is a statistical measure of how close the data are to the fitted
regression line
• Also known as the coefficient of determination
• Has a value between 0 and 1 for no-fit and perfect fit, respectively
𝑆𝑆𝑆𝑆𝑟𝑟𝑟𝑟𝑟𝑟 = �
𝑖𝑖
(𝑦𝑦𝑖𝑖 − �𝑦𝑦𝑖𝑖)2
𝑆𝑆𝑆𝑆𝑡𝑡𝑡𝑡𝑡𝑡 = �
𝑖𝑖
(𝑦𝑦𝑖𝑖 − �𝑦𝑦)2 , 𝑤𝑤ℎ𝑒𝑒𝑒𝑒𝑒𝑒 �𝑦𝑦 𝑖𝑖𝑖𝑖 𝑡𝑡ℎ𝑒𝑒 𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 𝑜𝑜𝑜𝑜 𝑡𝑡ℎ𝑒𝑒 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑
𝑅𝑅2 = 1 −
𝑆𝑆𝑆𝑆𝑟𝑟𝑟𝑟𝑟𝑟
𝑆𝑆𝑆𝑆𝑡𝑡𝑡𝑡𝑡𝑡

71. Dimensionality Reduction

72. Curse of dimensionality
Image from http://www.newsnshit.com/curse-of-dimensionality-interactive-demo/
when the dimensionality
increases  the volume
of the space increases so
fast that the available
data become sparse

73. Feature selection
• Comprehensive (all subsets)
• Forward stepwise
• Backward stepwise
• Forward-Backward
• Many more…

74. Features compression/projection
• Project to lower dimensional
space while preserving as
much information as possible
• Principle Component Analysis
(PCA)
• Unsupervised method
Image from http://compbio.pbworks.com/w/page/16252905/Microarray%20Dimension%20Reduction

75. Overfitting and Underfitting

76. Overfitting
x
y
square meter
Price(*1000)
x1
x2
High Variance

77. Underfitting
x1
x2
x
y
square meter
Price(*1000)
High Bias

78. Training vs. Testing Errors
•Accuracy on training set is not representative of
model performance
•We need to calculate the accuracy on the test
set (a new unseen examples)
•The goal is to generalize the model to work on
unseen data

79. Bias and variance trade-off
Model Complexity
error
Low High
Testing
Training
High Bias High Variance
The optimal is
to have low
bias and low
variance

80. Learning Curves
High Bias High Variance
Number of Training Samples
error
Low High
Validation
Training
Number of Training Sampleserror Low High
Validation
Training

81. Regularization
• To prevent overfitting
• Decrease the complexity of the model
• Example of regularized regression model (Ridge
Regression)
• 𝜆𝜆 is a very important hyper-parameter
𝑅𝑅𝑅𝑅𝑅𝑅 𝑤𝑤0, 𝑤𝑤1 = ∑𝑖𝑖=1
𝑁𝑁
(�𝑦𝑦𝑖𝑖 − 𝑦𝑦𝑖𝑖)2
+ 𝜆𝜆 ∑𝑗𝑗
𝑘𝑘
𝑤𝑤𝑗𝑗
2
,
𝑘𝑘 = 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤ℎ𝑡𝑡𝑡𝑡

82. Debugging a Learning Algorithm
• From “Machine Learning” course on coursera.org, by Andrew Ng
• Get more training examples  fixes high variance
• Try smaller sets of features  fixes high variance
• Try getting additional features  fixes high bias
• Try adding polynomial features (e.g., 𝑥𝑥1
2
, 𝑥𝑥2
2
, 𝑥𝑥1, 𝑥𝑥2, 𝑒𝑒𝑒𝑒𝑒𝑒)  fixes high
bias
• Try decreasing λ  fixes high bias
• Try increasing 𝜆𝜆  fixes high variance

84. What is the best ml algorithm?
•“No free lunch” theorem: there is no
one model that works best for every
problem
•We need to try and compare different
models and assumptions
•Machine learning is full of uncertainty

85. ‫ﻣﺘﻼزﻣﺔ‬‫وﯾﻜﺎ‬
Weka syndrome

86. ‫اﻵﻟﺔ‬ ‫ﺗﻌﻠﻢ‬ ‫ﻟﺘﻄﺒﯿﻖ‬ ‫ﻧﺼﺎﺋﺢ‬
•ً‫ا‬‫ﺟﯾد‬ ‫ﺣﻠﮭﺎ‬ ‫ﺑﺻدد‬ ‫أﻧت‬ ‫اﻟﺗﻲ‬ ‫اﻟﻣﺷﻛﻠﺔ‬ ‫اﻓﮭم‬
•‫اﻟﻣﺷﻛﻠﺔ؟‬ ‫ھﻲ‬ ‫ﻣﺎ‬
•‫ﺑﺎﻟﺿﺑط؟‬ ‫ﺣﻠﮫ‬ ‫اﻟﻣطﻠوب‬ ‫ﻣﺎ‬
•‫ﺑﺎﻟﻣﺟﺎل؟‬ ‫ﻣﺗﻌﻠﻘﺔ‬ ‫أﻣور‬ ‫ﺗﺗﻌﻠم‬ ‫أن‬ ‫ﺗﺣﺗﺎج‬ ‫ھل‬)،‫ﺗﺳوﯾﻖ‬ ،‫طﺑﻲ‬(...
•ً‫ا‬‫ﺟﯾد‬ ‫اﻟﻣﺗﺎﺣﺔ‬ ‫اﻟﺑﯾﺎﻧﺎت‬ ‫اﻓﮭم‬
•‫اﻟﺑﯾﺎﻧﺎت‬ ‫ﺣﺟم‬
•‫اﻟوﺻﻔﯾﺔ‬ ‫اﻹﺣﺻﺎءات‬ ‫ﺑﻌض‬ ‫إﺟراء‬)descriptive statistics(‫اﻟﺑﯾﺎﻧﺎت‬ ‫ﻋﻠﻰ‬
•‫ﻣﻌﮭﺎ؟‬ ‫ﺗﺗﻌﺎﻣل‬ ‫ﻛﯾف‬ ‫ﻧﺎﻗﺻﺔ؟‬ ‫أﺟزاء‬ ‫ﺗوﺟد‬ ‫ھل‬

87. ‫اﻵﻟﺔ‬ ‫ﺗﻌﻠﻢ‬ ‫ﻟﺘﻄﺒﯿﻖ‬ ‫ﻧﺼﺎﺋﺢ‬
•‫واﻟﺑﯾ‬ ‫اﻟﻣﺷﻛﻠﺔ‬ ‫وﺻف‬ ‫ﻋﻠﻰ‬ ً‫ء‬‫ﺑﻧﺎ‬ ‫ﻻﺧﺗﺑﺎرھﺎ‬ ‫ﺧوارزﻣﯾﺎت‬ ‫ة‬ّ‫د‬‫ﻋ‬ ‫ﺣدد‬‫ﺎﻧﺎت‬
‫اﻟﻣﺗﺎﺣﺔ‬
•Regression? Classification? Clustering? Other?
•‫ﺗﺣﺗﺎج‬ ‫ھل‬regularization‫؟‬
•‫اﻟﻣﻣﯾزة‬ ‫اﻟﺧﺻﺎﺋص‬features
•‫ﺗﺳﺗﺧﻠﺻﮭﺎ؟‬ ‫أن‬ ‫ﺗﺣﺗﺎج‬ ‫أم‬ ،‫ﺟﺎھزة‬ ‫ھﻲ‬ ‫ھل‬)‫ﻧﺻوص‬ ‫أو‬ ‫ﺻورة‬ ‫ﻣن‬ ً‫ﻼ‬‫ﻣﺛ‬(
•‫ﻟﺗﻘﻠﯾﻠﮭﺎ؟‬ ‫ﺗﺣﺗﺎج‬ ‫ھل‬)feature selection or projection(
•‫إﻟﻰ‬ ‫ﺗﺣﺗﺎج‬ ‫ھل‬scaling‫؟‬

88. ‫اﻵﻟﺔ‬ ‫ﺗﻌﻠﻢ‬ ‫ﻟﺘﻄﺒﯿﻖ‬ ‫ﻧﺼﺎﺋﺢ‬
•‫اﻻﺧﺗﺑﺎر‬ ‫ﺻﻣم‬
•‫اﻟﺑﯾﺎﻧﺎت؟‬ ‫ﺗﻘﺳم‬ ‫ﻛﯾف‬)60% training, 20% validation, 20% testing(
•Evaluation Measures
•Hyper-parameters selection (using validation split)
•Plot learning curves to asses bias and variance
•‫ﺗﻔﻌل؟‬ ‫ﻣﺎذا‬
•‫اﻟﺑﯾﺎﻧﺎت؟‬ ‫ﻣن‬ ‫اﻟﻣزﯾد‬
•‫ﻣزﺟﮭﺎ؟‬ ‫أو‬ ‫زﯾﺎدﺗﮭﺎ‬ ‫أو‬ ‫اﻟﺧﺻﺎﺋص‬ ‫ﺗﻘﻠﯾل‬
•‫اﻻﺧﺗﺑﺎر‬ ‫ﺑﯾﺎﻧﺎت‬ ‫ﻋﻠﻰ‬ ‫اﺧﺗرﺗﮭﺎ‬ ‫اﻟﺗﻲ‬ ‫اﻟﺧوارزﻣﯾﺎت‬ ‫طﺑﻖ‬ ،‫ھذا‬ ‫ﻛل‬ ‫ﻣن‬ ‫ﺗﻧﺗﮭﻲ‬ ‫أن‬ ‫ﺑﻌد‬testing
split‫اﻷﻧﺳب‬ ‫أﻧﮫ‬ ‫ﺗﻌﺗﻘد‬ ‫ﻣﺎ‬ ‫ﻣﻧﮭﺎ‬ ‫واﺧﺗر‬ ،

89. ‫اﻟﻤﺠﺎل‬ ‫ﻟﺘﻌﻠﻢ‬ ‫ﻣﻘﺘﺮح‬ ‫ﺑﺮﻧﺎﻣﺞ‬
•‫واﻹﺣﺻﺎء‬ ‫اﻟرﯾﺎﺿﯾﺎت‬ ‫ﻓﻲ‬ ‫اﻟﺗﺎﻟﯾﺔ‬ ‫اﻟﻣواﺿﯾﻊ‬ ‫ﻣراﺟﻌﺔ‬
•Descriptive Statistics
•Inferential Statistics
•Probability
•Linear Algebra
•Basics of differential equations
•‫ﻛﺗﺎب‬ ‫ﻗراءة‬:Python Machine Learning

90. ‫اﻟﻤﺠﺎل‬ ‫ﻟﺘﻌﻠﻢ‬ ‫ﻣﻘﺘﺮح‬ ‫ﺑﺮﻧﺎﻣﺞ‬
•‫دورة‬ ‫ﻓﻲ‬ ‫اﻟﺗﺳﺟﯾل‬“Machine Learning”‫ﻓﻲ‬coursera.org
•www.coursera.org/learn/machine-learning
•‫اﻟﺗﻣﺎرﯾن‬ ‫ﺟﻣﯾﻊ‬ ‫وﺣل‬
•‫اﻵﻟﺔ‬ ‫ﺑﺗﻌﻠم‬ ‫اﻟﻌﻼﻗﺔ‬ ‫ذات‬ ‫واﻟﻣﻛﺗﺑﺎت‬ ‫ﺑرﻣﺟﺔ‬ ‫ﻟﻐﺔ‬ ‫ﺗﻌﻠم‬
•Matlab
•Python
•R

91. ‫اﻟﻤﺠﺎل‬ ‫ﻟﺘﻌﻠﻢ‬ ‫ﻣﻘﺘﺮح‬ ‫ﺑﺮﻧﺎﻣﺞ‬
•‫ﻓﻲ‬ ‫اﻟﺗﺳﺟﯾل‬‫ﻛﺎﺟل‬)www.kaggle.com(‫اﻟﺑﯾﺎﻧﺎت‬ ‫ﺑﻌض‬ ‫ﻋﻠﻰ‬ ‫واﻟﻌﻣل‬ ،
‫اﻟﻣﺗﺎﺣﺔ‬ ‫واﻟﺗﺣدﯾﺎت‬.
•‫ﻟﻠﺑداﯾﺔ‬ ‫ﻣﻘﺗرح‬:
•Titanic: Machine Learning from Disaster
https://www.kaggle.com/c/titanic
•House Prices: Advanced Regression Techniques
https://www.kaggle.com/c/house-prices-advanced-regression-
techniques
•Digit Recognizer
https://www.kaggle.com/c/digit-recognizer

92. ‫اﻟﻤﺠﺎل‬ ‫ﻟﺘﻌﻠﻢ‬ ‫ﻣﻘﺘﺮح‬ ‫ﺑﺮﻧﺎﻣﺞ‬
•‫ﺗﺣﺗﺎﺟﮭﺎ‬ ‫أﻧك‬ ‫اﻵن‬ ‫ﺗﻌرف‬ ‫اﻟﺗﻲ‬ ‫اﻷﻣور‬ ‫ﻟﺗﻘوﯾﺔ‬ ‫واﻟرﯾﺎﺿﯾﺎت‬ ‫ﻟﻺﺣﺻﺎء‬ ‫أﺧرى‬ ‫ﻣراﺟﻌﺔ‬
•‫اﻵﻟﺔ‬ ‫ﻟﺗﻌﻠم‬ ‫ﻣﻘﺗرﺣﺔ‬ ‫أﺧرى‬ ‫ﻛﺗب‬)ً‫ﺎ‬‫ﺗﻘدﻣ‬ ‫أﻛﺛر‬(

93. ‫اﻟﻤﺠﺎل‬ ‫ﻟﺘﻌﻠﻢ‬ ‫ﻣﻘﺘﺮح‬ ‫ﺑﺮﻧﺎﻣﺞ‬
•‫ﺗرﯾده‬ ‫ﻣﺟﺎل‬ ‫ﻋﻠﻰ‬ ‫اﻟﺗرﻛﯾز‬
•‫ﻟﻸﻋﻣﺎل‬ ‫اﻟﻣﺳﺗﻘﺑﻠﻲ‬ ‫اﻟﺗﻧﺑؤ‬)‫ﻛﺎﻟﺗﺳوﯾﻖ‬(
•‫اﻟطﺑﯾﻌﯾﺔ‬ ‫اﻟﻠﻐﺎت‬ ‫ﻣﻌﺎﻟﺟﺔ‬
•‫اﻟﺣﺎﺳب‬ ‫رؤﯾﺔ‬
•‫أﻋﻣﺎﻟك‬ ‫ﻧﺗﺎﺋﺞ‬ ‫اﻋرض‬
•‫ﻋﻣﻠك‬ ‫اﻟﻧﺎس‬ ‫ﺷﺎرك‬)‫واﻟﻧﺗﺎﺋﺞ‬ ‫اﻟﻛود‬ ‫ﻣﺛل‬(‫رأﯾﮭم‬ ‫واطﻠب‬
•‫ﺑﮫ‬ ‫ﺗﺧﺻﺻت‬ ‫اﻟذي‬ ‫اﻟﻣﺟﺎل‬ ‫ﻓﻲ‬ ‫دورة‬ ‫أﻗم‬

94. ‫وإﻧﺼﺎﺗﻜﻢ‬ ‫ﺣﻀﻮرﻛﻢ‬ ‫ﻋﻠﻰ‬ ‫ﻟﻜﻢ‬ ً‫ا‬‫ﺷﻜﺮ‬