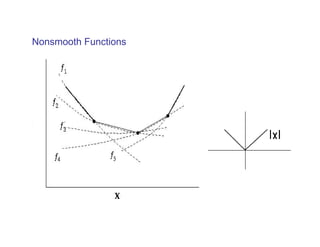
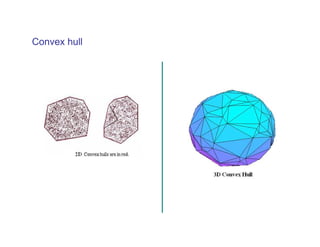
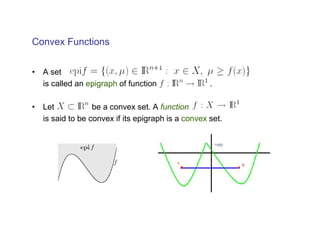
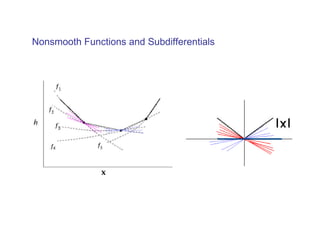
The document summarizes presentations on nonsmooth optimization, robust optimization, and derivative-free optimization given at the 4th International Summer School in Kiev, Ukraine. Gerhard Weber and Basak Akteke-Ozturk presented on nonsmooth optimization and its applications in clustering problems. Robust optimization approaches were discussed for problems with uncertain parameters. Methods for minimizing functions without computing derivatives, known as derivative-free optimization, were also covered. Examples included trust-region algorithms and using models based on interpolation. Semidefinite programming relaxations for support vector clustering were mentioned.

1. 4th International Summer School
Achievements and Applications of Contemporary
Informatics, Mathematics and Physics
National University of Technology of the Ukraine
Kiev, Ukraine, August 5-16, 2009
Nonsmooth Optimization
Derivative Free Optimization and Robust Optimization
Gerhard-Wilhelm Weber * and Başak Akteke-Öztürk
Gerhard- Akteke-
Institute of Applied Mathematics
Middle East Technical University, Ankara, Turkey
* Faculty of Economics, Management and Law, University of Siegen, Germany
Center for Research on Optimization and Control, University of Aveiro, Portugal

2. Introduction
Mathematical Models
• Experimental Data Analysis
• Classification problems
• Identification problems treated by:
• Pattern Recognition SVM, Cluster Analysis,
• Assignment and Allocation
Neural Systems etc.
• When these methods were born, the most developed and popular
optimization tools were Linear and Quadratic Programming.
• Optimization parts of these methods are reduced to LP and QP
Linear Discriminant Analysis

3. Introduction
• progress in Optimization • new advanced tools,
• Nonsmooth Analysis and • construct a mathematical model
Nondifferentiable Opt. better suited for the problem
under consideration
• Most cases clustering problems are reduced
to solving nonsmooth optimization problems.
• We are interested in new methods for solving related nonsmooth
problems
(e.g.,
Semidefinite Programming, Semi-Infinite Programming,
discrete gradient method and cutting angle method).

4. Nonsmooth Optimization
Problem:
minimize
subject to
• : is nonsmooth at many points of interest
do not have a conventional derivative at these points.
• A less restrictive class of assumptions for than smoothness:
convexity and Lipschitzness.

5. Nonsmooth Functions

6. Convex Sets
A set is called convex
if

7. Convex Sets
• The convex hull of a set :
• The sets and coincide if and only if is convex.
• The set is called a cone if for all , ;
i.e.,
contains all positive multiples of its elements.

8. Convex hull

9. Convex Functions
• A set
is called an epigraph of function .
• Let be a convex set. A function
is said to be convex if its epigraph is a convex set.

10. Convex Functions
• are differentiable (smooth) almost everywhere,
• their minimizers are points where the function need not be
differentiable,
• standard numerical methods do not work
• Examples of convex functions:
– affinely linear:
– quadratic: (c>0)
– exponential:

11. Convex Functions

12. Convex Optimization
• minimizing a convex function over a convex feasible set
• Many applications.
• Important, because:
a strong duality theory
any local minimum is a global minimum
includes least-squares problems and linear programs as special cases
can be solved efficiently and reliably

13. Lipschitz Continuous
• A function is called (locally) Lipschitz continuous, if
for any bounded there exist a constant such that
• Lipschitzness is a more restrictive property on functions than
continuity, i.e., all Lipschitz functions are continuous, but
they are not guaranteed to be smooth.
• They possess a generalized gradient.

14. Lipschitz Continuous

15. Nonsmooth Optimization
• We call the the set ∂f(x) subdifferential of f at x
• Any vector v є ∂f(x) is a subgradient.
• A proper convex function f is subdifferentiable at any point x є , if
∂f(x) is non-empty, convex and compact at x.
• If the convex function f is continuously differentiable, then

16. Nonsmooth Functions and Subdifferentials

17. Generalized Derivatives
• The generalized directional derivative of f at x in the direction g is
defined as
• If the function f is locally Lipschitz continuous, then the generalized
directional derivative exists.
• The set
is called the (Clarke) subdifferential of the function f at a point

18. Nonsmooth Optimization
Nonsmooth optimization
– more general problem of minimizing functions,
– lack some, but not all, of the favorable properties of convex functions,
– minimizers often are again points where the function is nondifferentiable.

19. Cluster Analysis via Nonsmooth Opt.
Given
Problem:
This is a partitioning clustering problem.

20. Clustering

21. Clustering

22. Cluster Analysis via Nonsmooth Opt.
• k is the number of clusters (given),
• m is the number of available patterns (given),
• is the j-th cluster’s center (to be found),
• association weight of pattern , cluster j (to be found):
• ( ) is an matrix,
• objective function has many local minima.

23. Cluster Analysis via Nonsmooth Opt.
Suggestion (if k is not given a priori):
• Start from a small enough number of clusters k and gradually
increase the number of clusters for the analysis until a certain
stopping criteria met.
• This means: If the solution of the corresponding optimization
problem is not satisfactory, the decision maker needs to consider a
problem with k + 1 clusters, etc..
• This implies: One needs to solve repeatedly arising optimization
problems with different values of k - a task even more challenging.
• In order to avoid this difficulty, we suggest a step-by-step calculation
of clusters.

24. Cluster Analysis via Nonsmooth Opt.
• k-means, h-means, j-means
• dynamic programming
• branch and bound
• cutting planes
• metaheuristics: simulated annealing, tabu search and genetic algorithms
• an interior point method for minimum sum-of squares clustering
problem
• agglomerative and divisive hierarchical clustering incremental approach

25. Cluster Analsysis via Nonsmooth Opt.
Reformulated Problem:
• A very complicated objective function: nonsmooth and nonconvex.
• The number of variables in the nonsmooth optimization approach is
k×n, before it was (m+n)×k.

26. Robust Optimization
• There is uncertainty or variation in the objective and constraint
functions, due to parameters or factors that are either
beyond our control or unknown.
• Refers to the ability of the subject to cope well with uncertainties
in linear, conic and semidefinite programming .
• Applications in control, engineering design and finance.
• Convex, modelled by SDP or cone quadratic programming.
• Robust solutions are computed in polynomial time, via (convex)
semidefinite programming problem.

27. Robust Optimization
• Let us examine Robust Linear Programming
• By a worst case approach the objective is the maximum over all
possible realizations of the objective
• A robust feasible solution with the smallest possible value of the f(x)
is sought.
• Robust optimization is no longer a linear programming.
The problem depends on the geometry of the uncertainty set U;
i.e.,
if U is defined as an ellipsoid, the problem becomes a
conic quadratic program.

28. Robust Optimization

29. Robust Optimization
• Considers that the uncertain parameter c belongs to a bounded, convex,
uncertainty set
• Stochastic Optimization: expected values,
parameter vector u is modeled as a random variable with known distribution
Robust Counterpart
• Worst Case Optimization: the robust solution is the one that has the best
worst case, i.e., it solves

30. Robust Optimization
• A complementary alternative to stochastic programming.
• Seeks a solution that will have a “good” performance under
many/most/all possible realizations of the uncertain input
parameters.
• Unlike stochastic programming, no distribution assumptions on
uncertain parameters –
each possible value equally important (this can be good or bad)
• Represents a conservative viewpoint when it is worst-case oriented.

31. Robust Optimization
• Especially useful when
– some of the problem parameters are estimates and carry estimation
risk,
– there are constraints with uncertain parameters that must be satisfied
regardless of the values of these parameters,
– the objective functions / optimal solutions are particularly sensitive to
perturbations,
– decision-maker can not afford low-probability high-magnitude risks.

32. Derivative Free Optimization
The problem is to minimize a nonlinear function of several variables
• the derivatives (sometimes even the values) of this function
are not available,
• arise in modern physical, chemical and econometric measurements and in
engineering applications,
• computer simulation is employed for the evaluation of the function values.
The methods are known as derivative free methods (DFO).

33. Derivative Free Optimization
Problem:
• cannot be computed or just does not exist for every x ,
• is an arbitrary subset of ,
• is called the easy constraint,
• the functions represent difficult constraints.

34. Derivative Free Optimization
Derivative free methods
• build a linear or quadratic model of the objective function,
• apply a trust-region or a line-search to optimize the model;
derivative based methods
use a Taylor polynomial -based model;
DFO methods use interpolation, regression
or other sample-based models.

35. Derivative Free Optimization
Six iterations of a trust-region algorithm.

36. Semidefinite Programming
• Optimization problems where the variable is not a vector but a
symmetric matrix which is required to be positive semidefinite.
• Linear Programming
Semidefinite Programming
vector of variables
a symmetric matrix
nonnegativity constraint
a positive semidefinite constraint
• SDP is convex, has a duality theory and can be solved
by interior point methods.

37. SVC via Semidefinite Programming
• I try to reformulate the support vector clustering problem as a
convex integer program and then relax it to a soft clustering
formulation which can be feasibly solved by a 0-1 semidefinite
program.
• In the literature, k-means and clustering methods which use a
graph cut model are reformulated as a semidefinite program
and solved by using semidefinite programming relaxations.

38. Some References
1. Aharon Ben-Tal and Arkadi Nemirovski, Robust optimization
methodology and applications.
2. Adil Bagirov, Nonsmooth optimization approaches in data
Classification.
3. Adil Bagirov, Derivative-free nonsmooth optimization and its
applications.
4. A. M. Bagirov, A. M. Rubinov, N.V. Soukhoroukova and J.
Yearwood, Unsupervised and supervised data classification via
nonsmooth and global optimization.
5. Laurent El Ghaoui, Robust Optimization and Applications.
6. Başak A. Öztürk, Derivative Free Optimization methods:
Application in Stirrer Configuration and Data Clustering.

39. Thank you very much!
Questions, please?