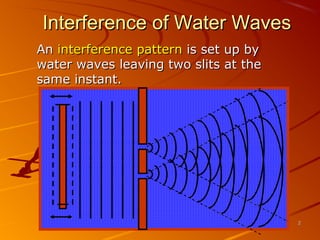
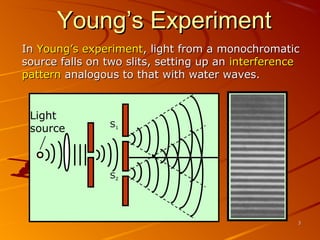
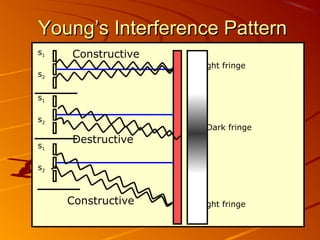
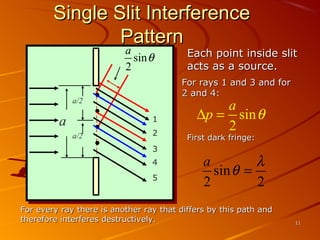
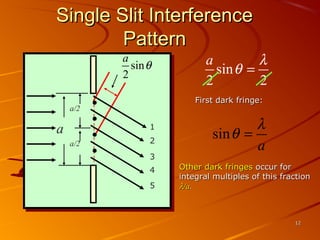
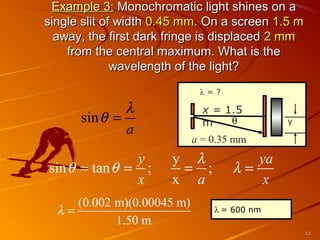
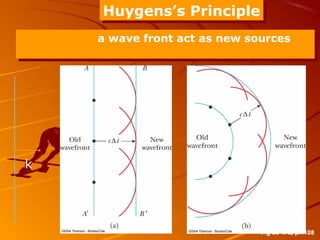
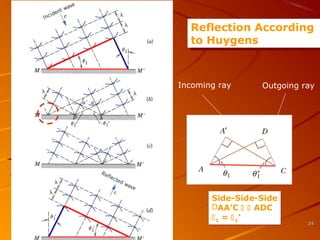
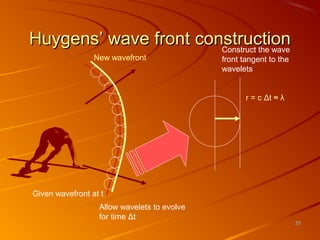
The document discusses several key properties of light: 1) Interference and polarization of light are examined through experiments like Young's slits and using polarizers. Interference creates light and dark fringes depending on the path difference between waves. 2) Huygens' principle is introduced as explaining how secondary wavelets propagate light in a manner consistent with laws of reflection and refraction. Each point on a wavefront acts as a secondary source. 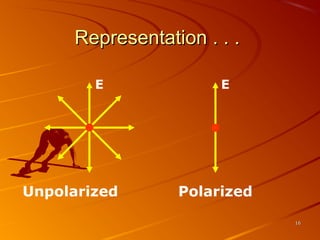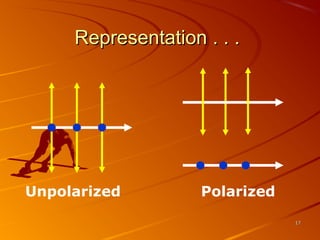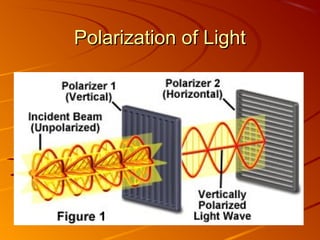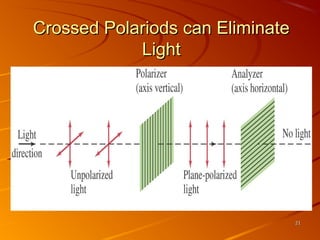3) Polarization occurs when unpolarized light passes through a filter, causing vibrations of the electric field to lie in one plane rather than randomly oriented planes. Crossed polarizers can eliminate transmitted light.

1. PROPERTIES OF LIGHT
Interference
Polarization
Huygens's Principle
Prepared by:
Karen A. Adelan
BSE 3

2. Interference of Water Waves
An interference pattern is set up by
water waves leaving two slits at the
same instant.
2

3. Young’s Experiment
In Young’s experiment, light from a monochromatic
source falls on two slits, setting up an interference
pattern analogous to that with water waves.
Light
source
S1
S2
3

4. The Superposition Principle
• The resultant displacement of two simul-taneous
waves (blue and green) is the algebraic sum of the
two displacements.
• The composite wave is shown in yellow.
Constructive
Interference
Destructive
Interference
The superposition of two coherent light waves
results in light and dark fringes on a screen.
4

5. Young’s Interference Pattern
s1
Constructive
Bright fringe
s2
s1
s2
s1
Dark fringe
Destructive
s2
Constructive
Bright fringe
5

6. Conditions for Bright Fringes
Bright fringes occur when the difference in path ∆p is
an integral multiple of one wave length λ.
p1
λ
λ
λ
p2
p3
p4
Path difference
∆p = 0, λ , 2λ, 3λ, …
Bright fringes:
∆p = nλ, n = 0, 1, 2, . . .
6

7. Conditions for Dark Fringes
Dark fringes occur when the difference in path ∆p is an
odd multiple of one-half of a wave length λ/2.
λ
2
p1
p2
p3
λ
λ
p3
Dark fringes:
λ
∆p = n
2
λ
∆p = n
2
n=
odd
n=
1,3,5 …
n = 1, 3, 5, 7, . . .
7

8. Analytical Methods for Fringes
x
d sin θ
s1
d
s2
Path difference
determines light and
dark pattern.
θ
p1
y
p2
∆p = p1 – p2
∆p = d sin θ
Bright fringes: d sin θ = nλ, n = 0, 1, 2, 3, . . .
Dark fringes:
d sin θ = nλ/2 , n = 1, 3, 5, . . .
8

9. Analytical Methods (Cont.)
From geometry, we
recall that:
x
d sin θ
s1
d
s2
θ
p1
y
p2
y
sin θ ≈ tan θ =
x
So that . . .
dy
d sin θ =
x
Bright fringes:
dy
= nλ , n = 0, 1, 2, ...
x
Dark fringes:
dy
λ
= n , n = 1, 3, 5...
x
2
9

10. Interference From Single Slit
When monochromatic light strikes a single slit, diffraction from the
edges produces an interference pattern as illustrated.
Relative intensity
Pattern Exaggerated
The interference results from the fact that not all paths of light
travel the same distance some arrive out of phase.
10

11. Single Slit Interference
Pattern
a
sin θ
2
For rays 1 and 3 and for
2 and 4:
a/2
a
1
a/2
Each point inside slit
acts as a source.
2
3
4
5
a
∆p = sin θ
2
First dark fringe:
a
λ
sin θ =
2
2
For every ray there is another ray that differs by this path and
therefore interferes destructively.
11

12. Single Slit Interference
Pattern
a
sin θ
2
First dark fringe:
a/2
a
1
a/2
a
λ
sin θ =
2
2
2
3
4
5
λ
sin θ =
a
Other dark fringes occur for
integral multiples of this fraction
λ/a.
12

13. Example 3: Monochromatic light shines on a
single slit of width 0.45 mm. On a screen 1.5 m
away, the first dark fringe is displaced 2 mm
from the central maximum. What is the
wavelength of the light?
λ=?
λ
sin θ =
a
y
sin θ ≈ tan θ = ;
x
x = 1.5
θ
m
y
a = 0.35 mm
y λ
= ;
x a
(0.002 m)(0.00045 m)
λ=
1.50 m
ya
λ=
x
λ = 600 nm
13

14. POLARIZATION
Polarized vs. Unpolarized
Unpolarized light: light wave which
is vibrating in more than one plane
Polarized light: light waves in
which the vibrations occur in a single
plane.
Polarization: The process of
transforming unpolarized light into
polarized light is known as
14

15. Polarized Light
Polarized Light
Vibrations lie on one
single plane only.
Unpolarized Light
Superposition of many
beams, in the same
direction of propagation,
but each with random
polarization.
15

16. Representation . . .
E
Unpolarized
E
Polarized
16

17. Representation . . .
Unpolarized
Polarized
17

18. Polarization of Light
18

19. Selective Absorption
Unpolarized
Light
Vertical
Compone
nt being
Transmitt
ed
Horizontal
Component being
Absorbed
19

20. Polarization by Absorption
Polaroid crystalline materials absorb
more light in one incident plane than
another, so that light progressing
through the material become more
and more polarized
20

21. Crossed Polariods can Eliminate
Light
21

22. Huygens’ Principle
The first person to explain how wave
theory can also account for the laws of
geometric optics was Christian Huygens in
1670.
The principle states that:
Every point on a wave-front may be
considered a source of secondary spherical
wavelets which spread out in the forward
direction at the speed of light. The new
wave-front is the tangential surface to all
of these secondary wavelets.
22

23. Huygens’s Principle
Huygens’s Principle
All points on a wave front act as new sources
All points on a wave front act as new sources
for the production of spherical secondary waves
for the production of spherical secondary waves
k
23
Fig 35-17a, p.1108

24. Reflection According
Reflection According
to Huygens
to Huygens
Incoming ray
Outgoing ray
Side-Side-Side
DAA’C   ADC
 1 =  1’
24

25. Huygens’ wave front construction
Construct the wave
New wavefront
front tangent to the
wavelets
r = c Δt ≈ λ
Given wavefront at t
Allow wavelets to evolve
for time Δt
25