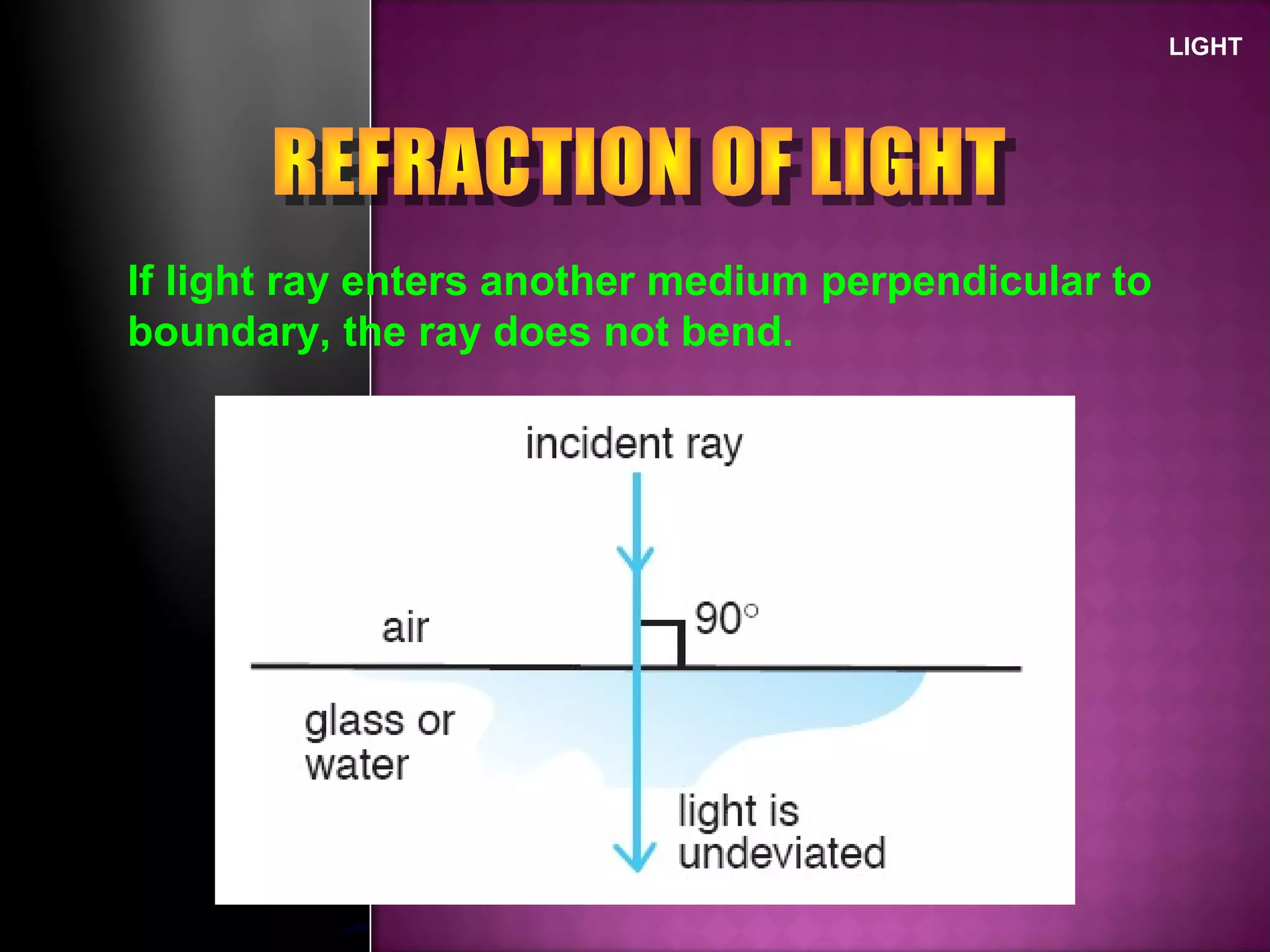
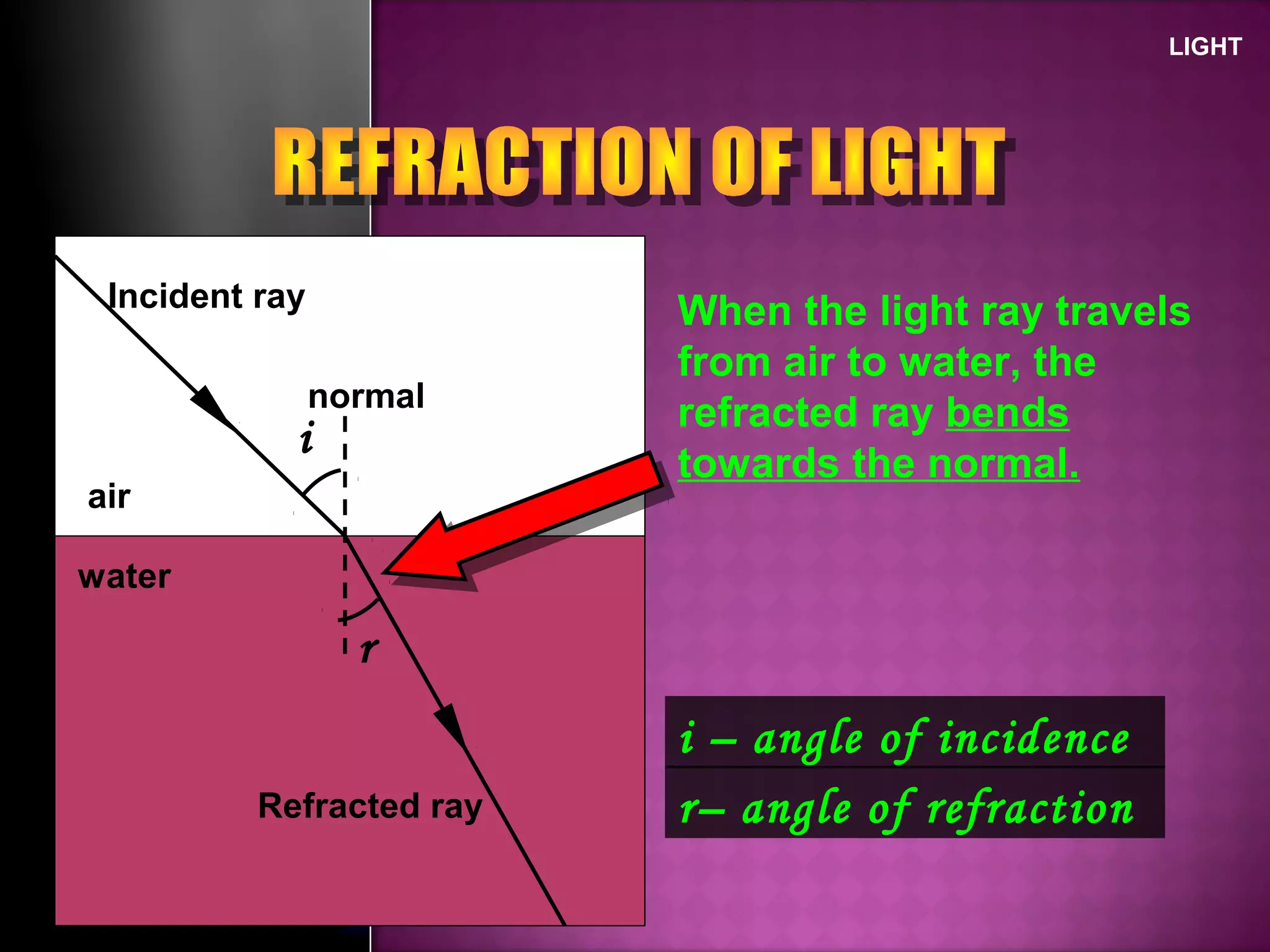
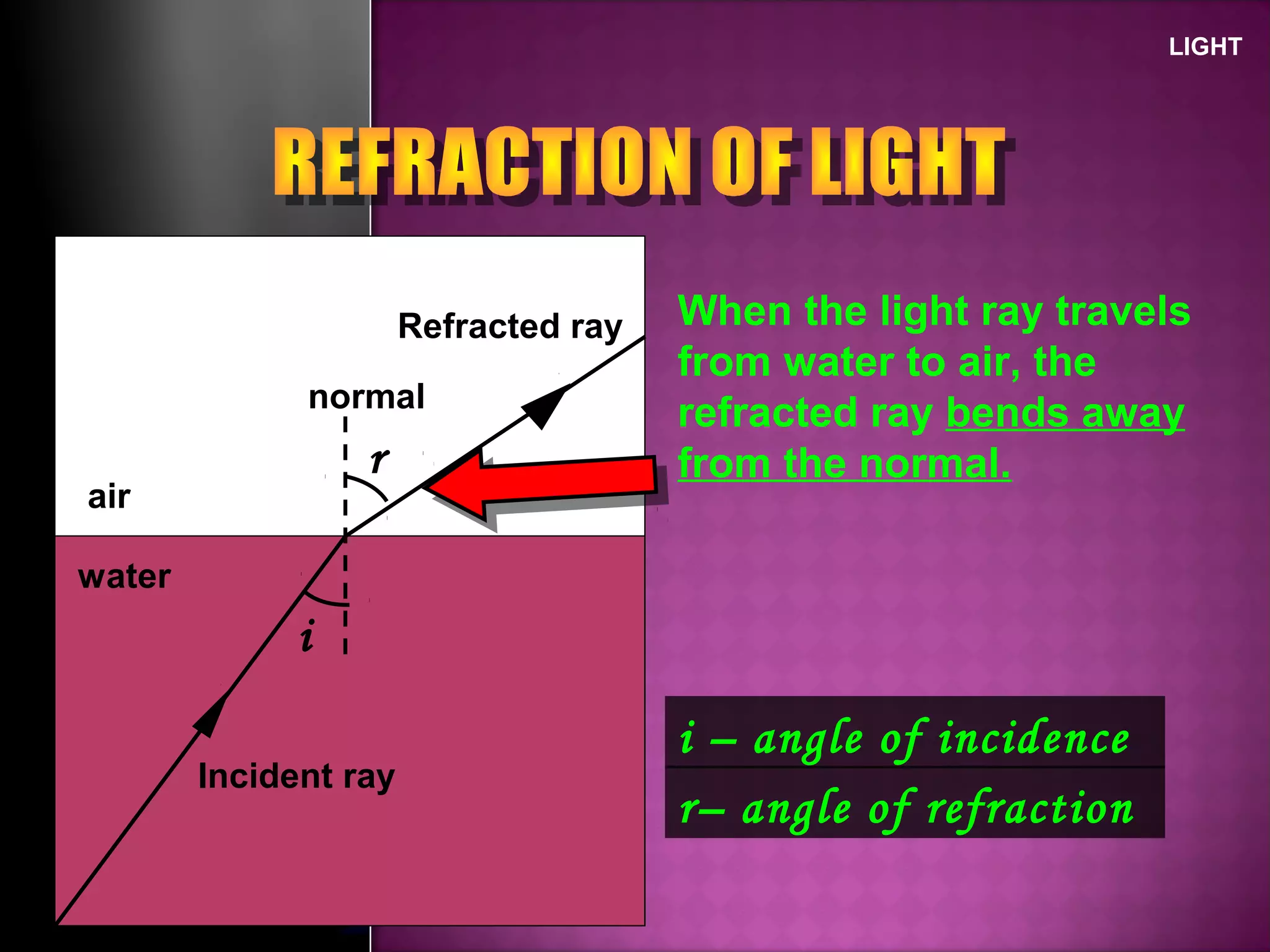
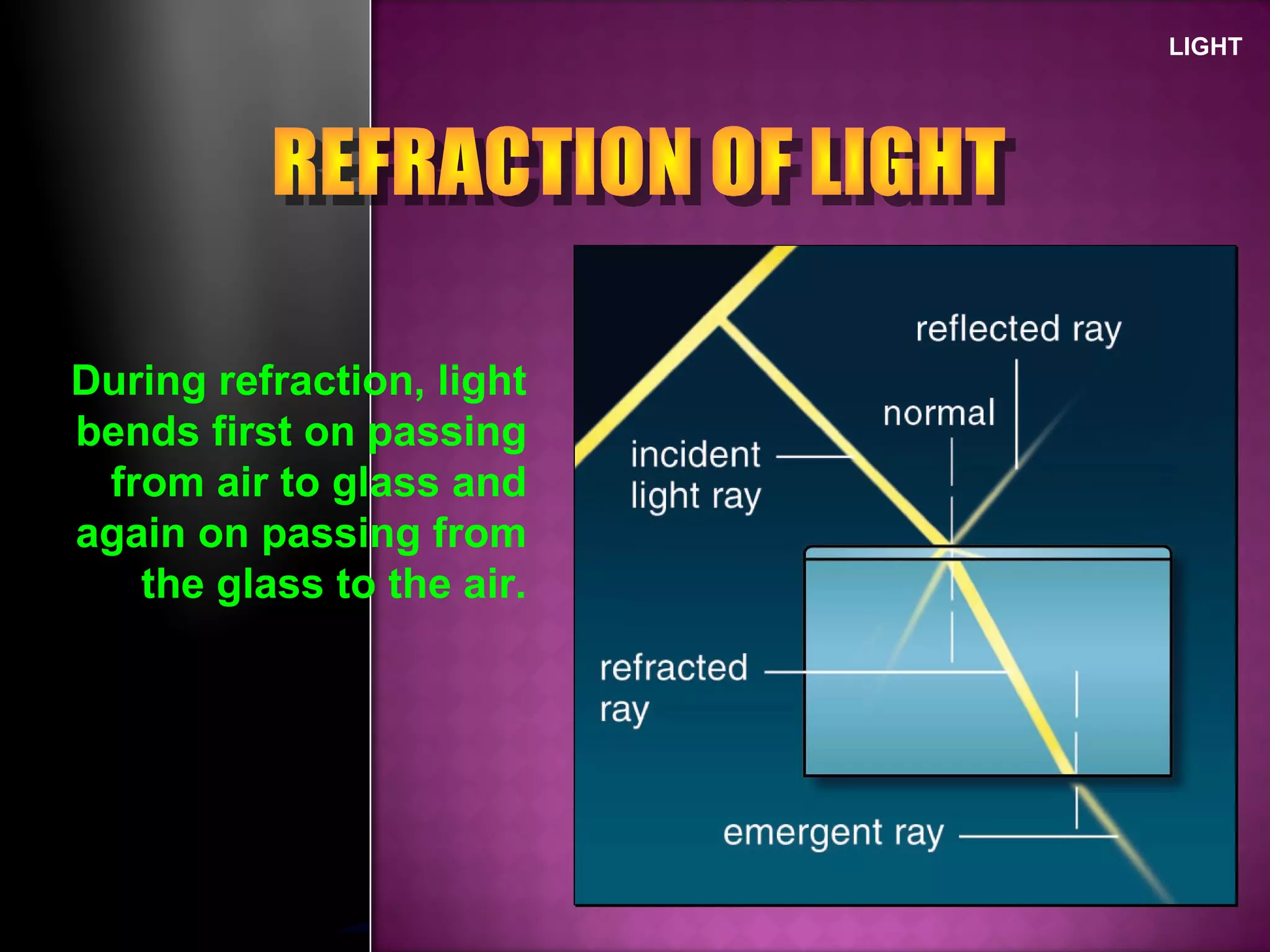
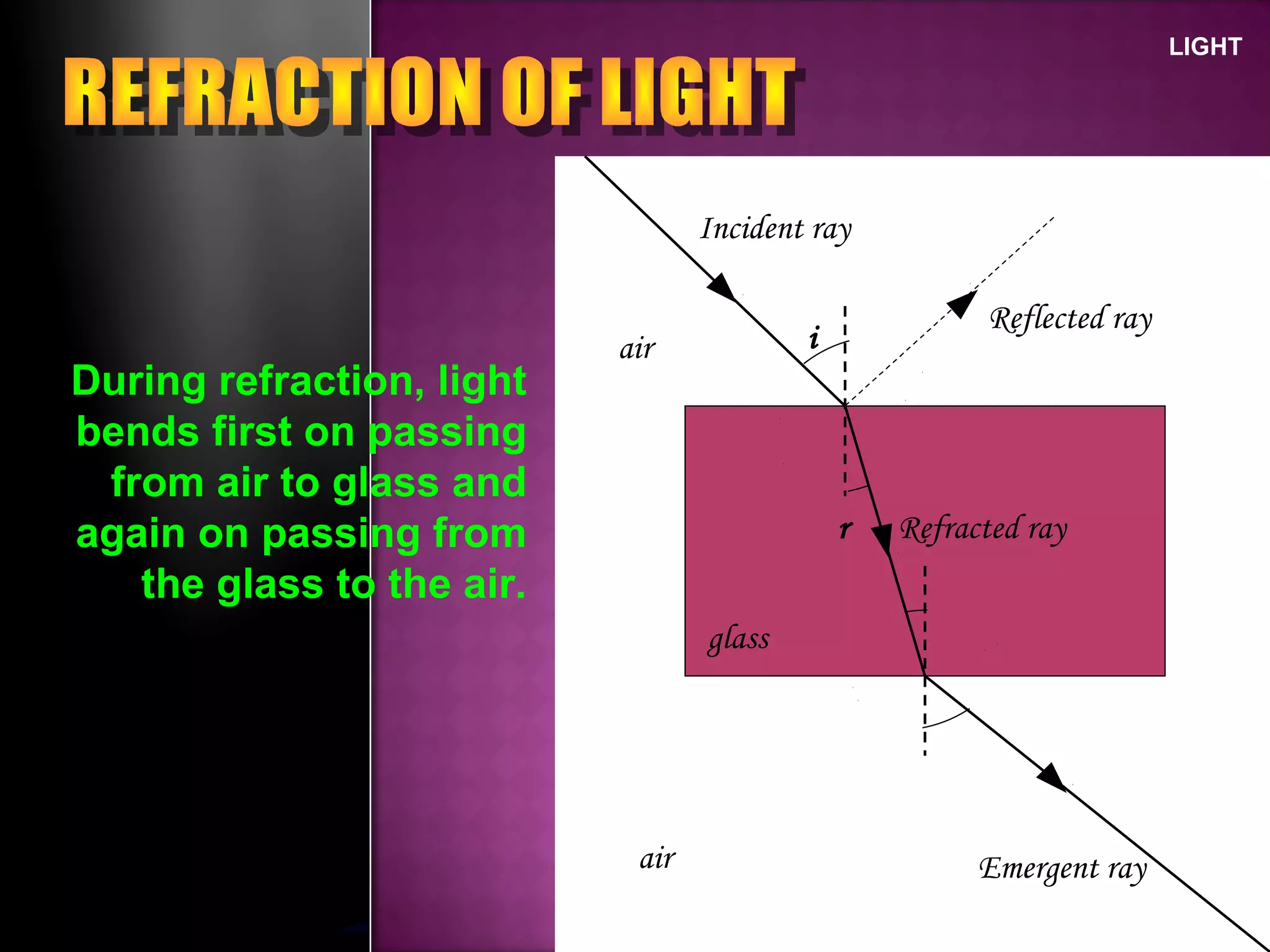
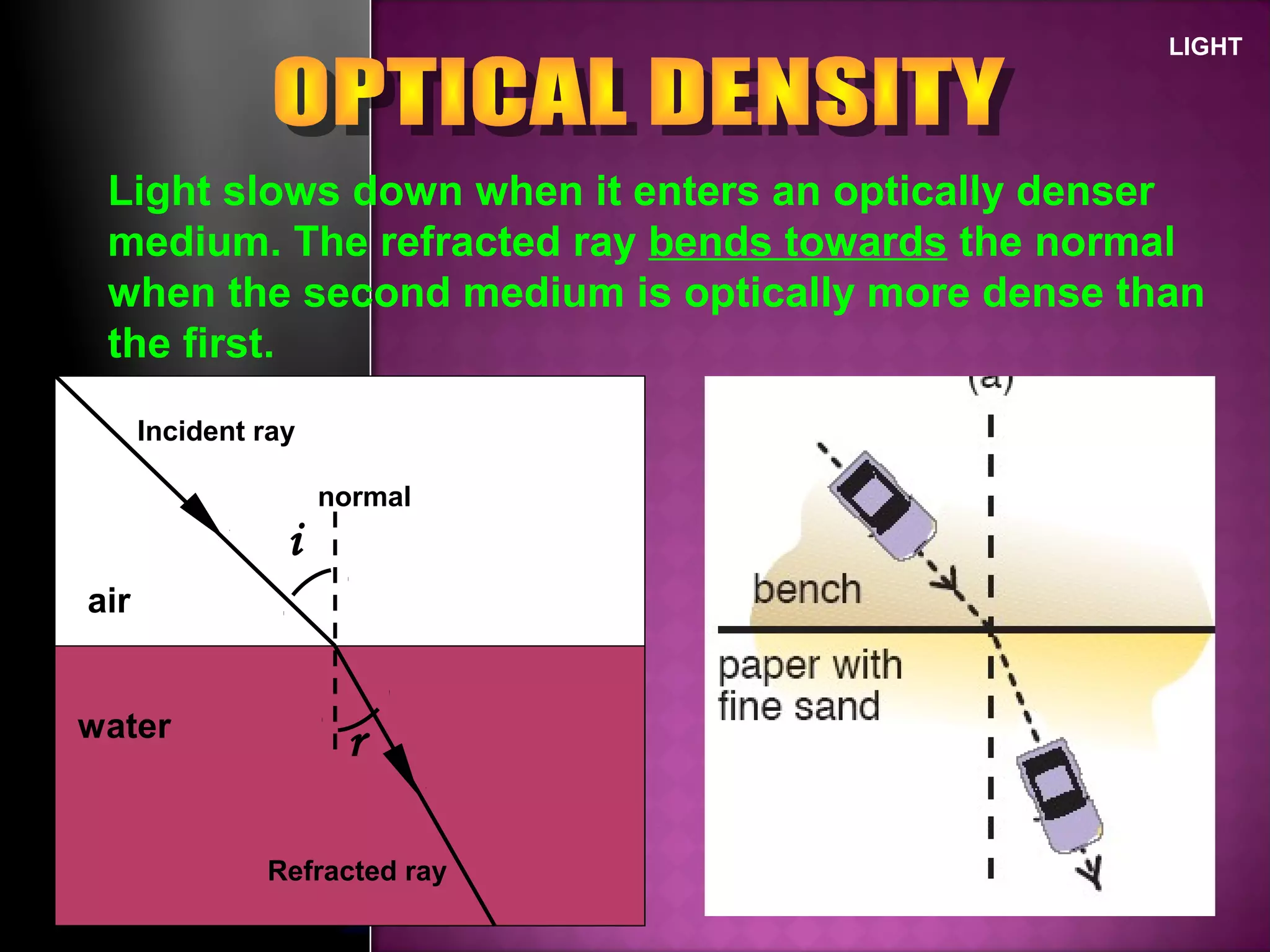
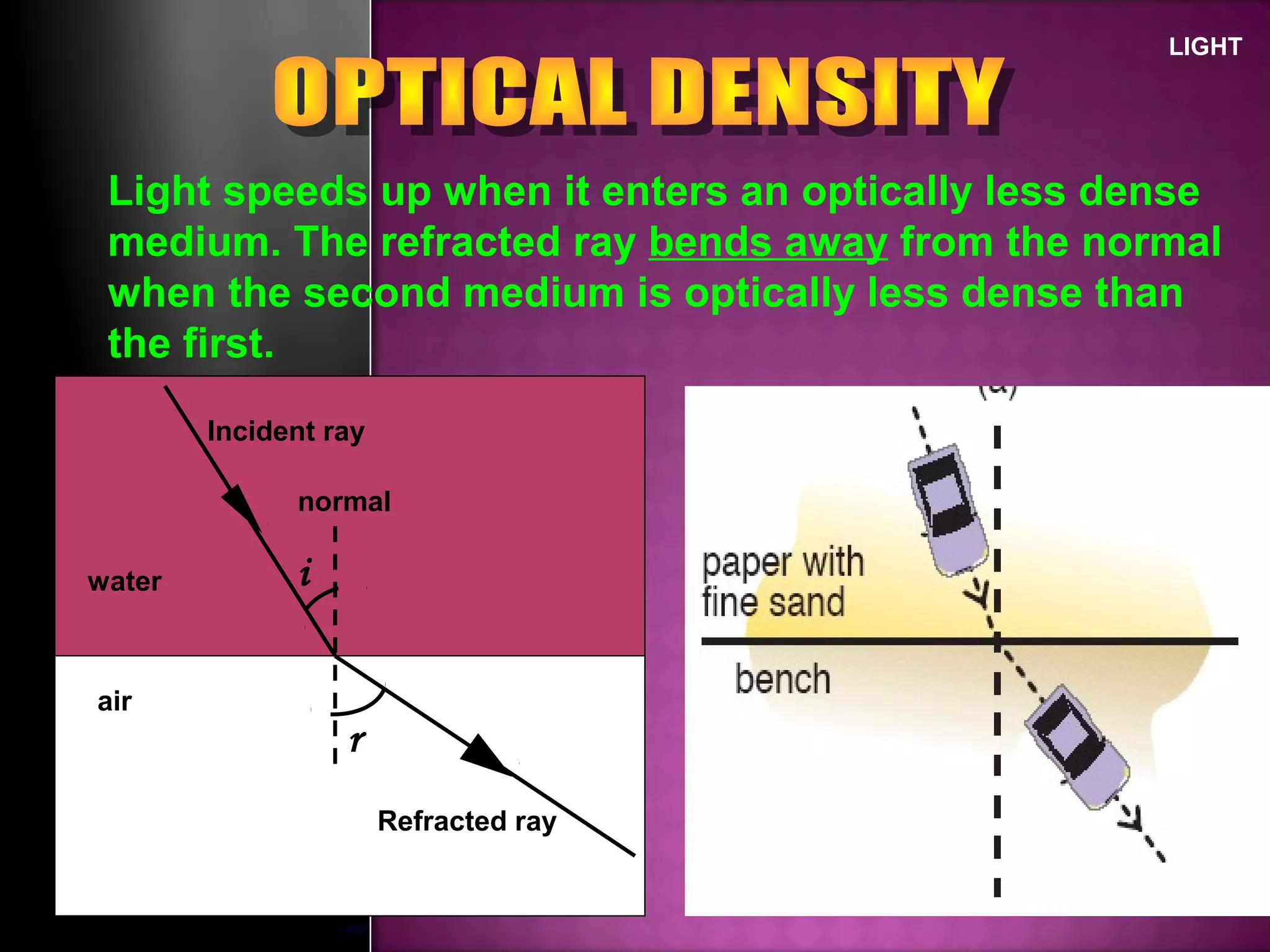
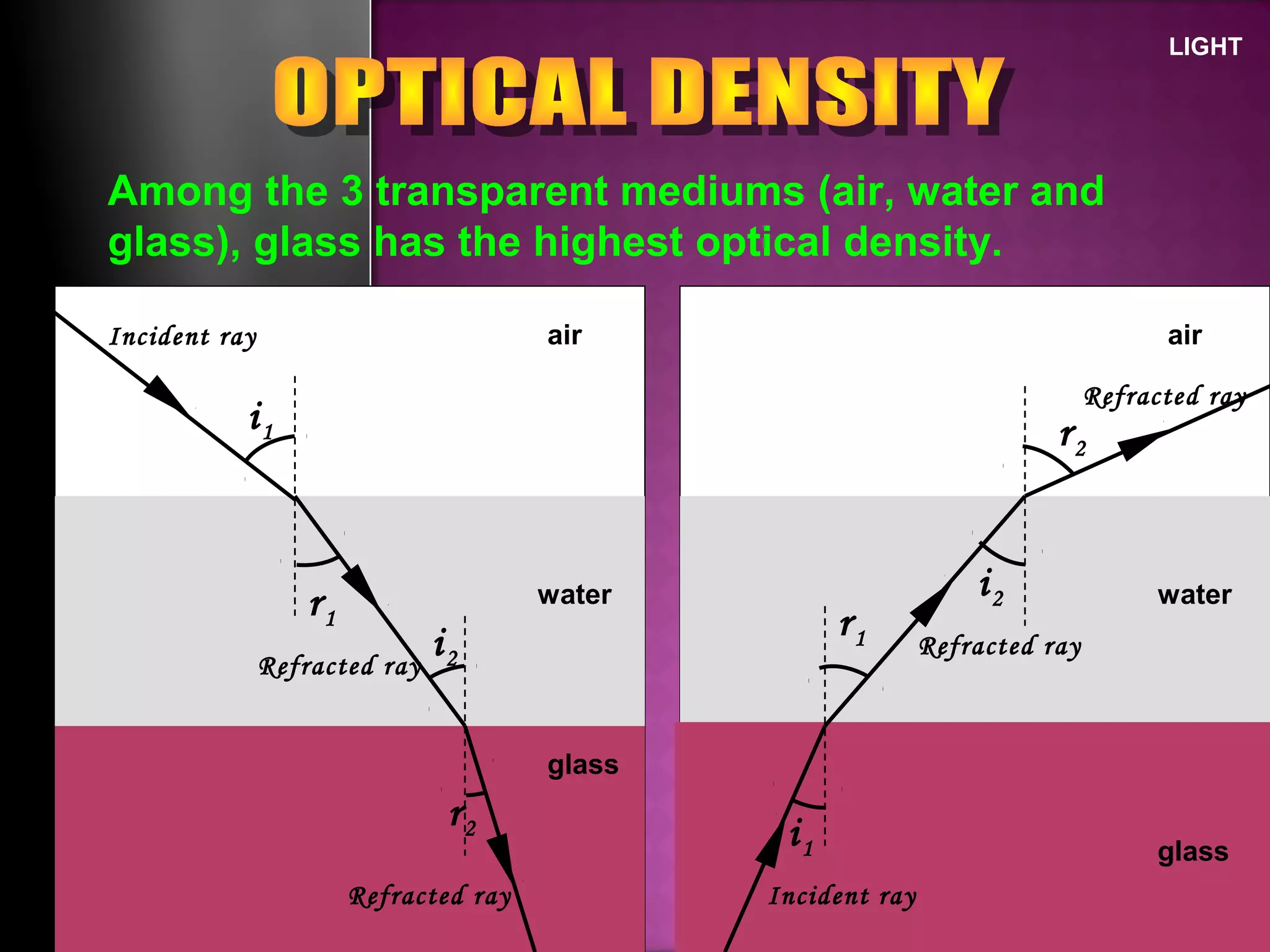
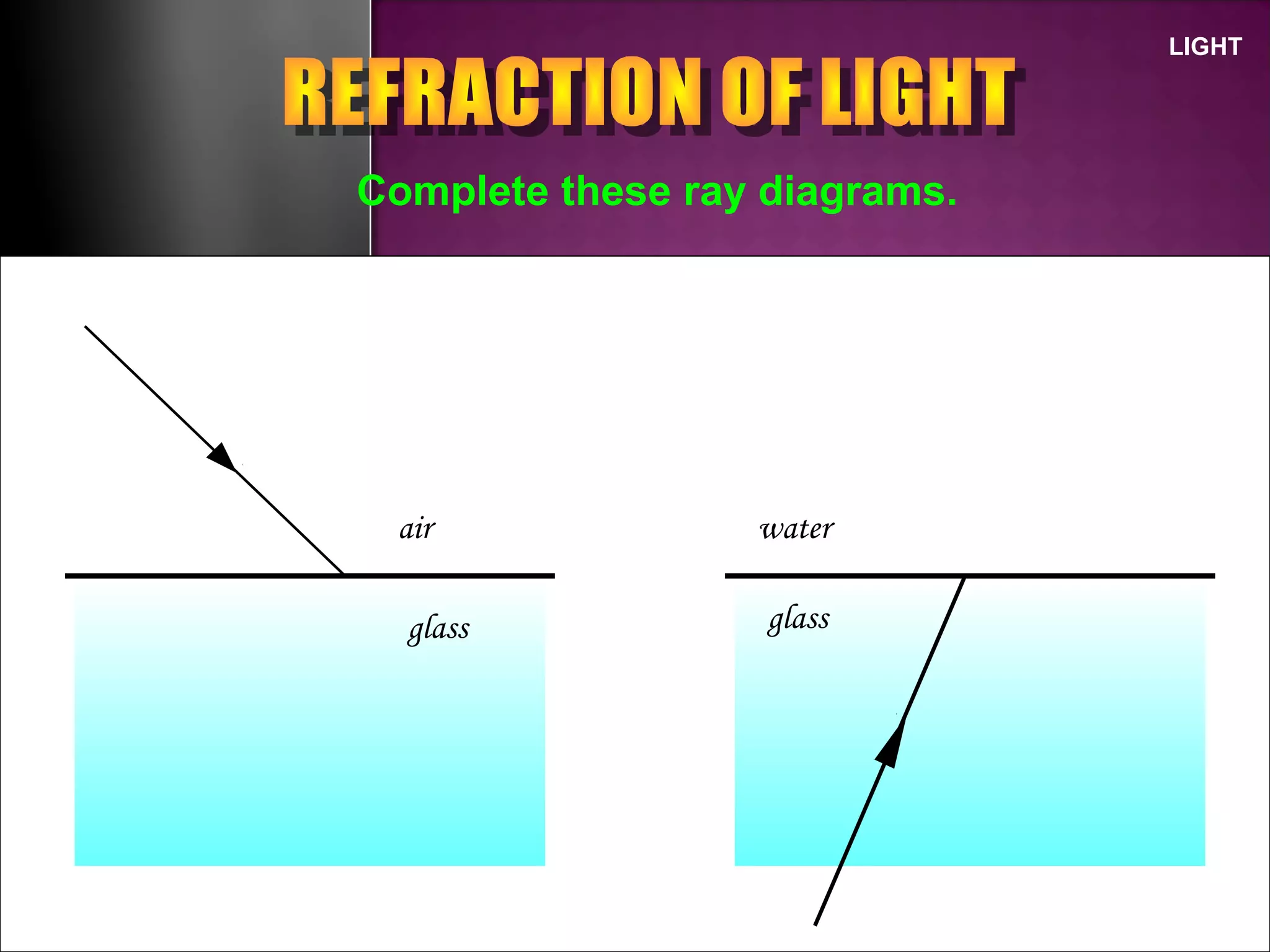
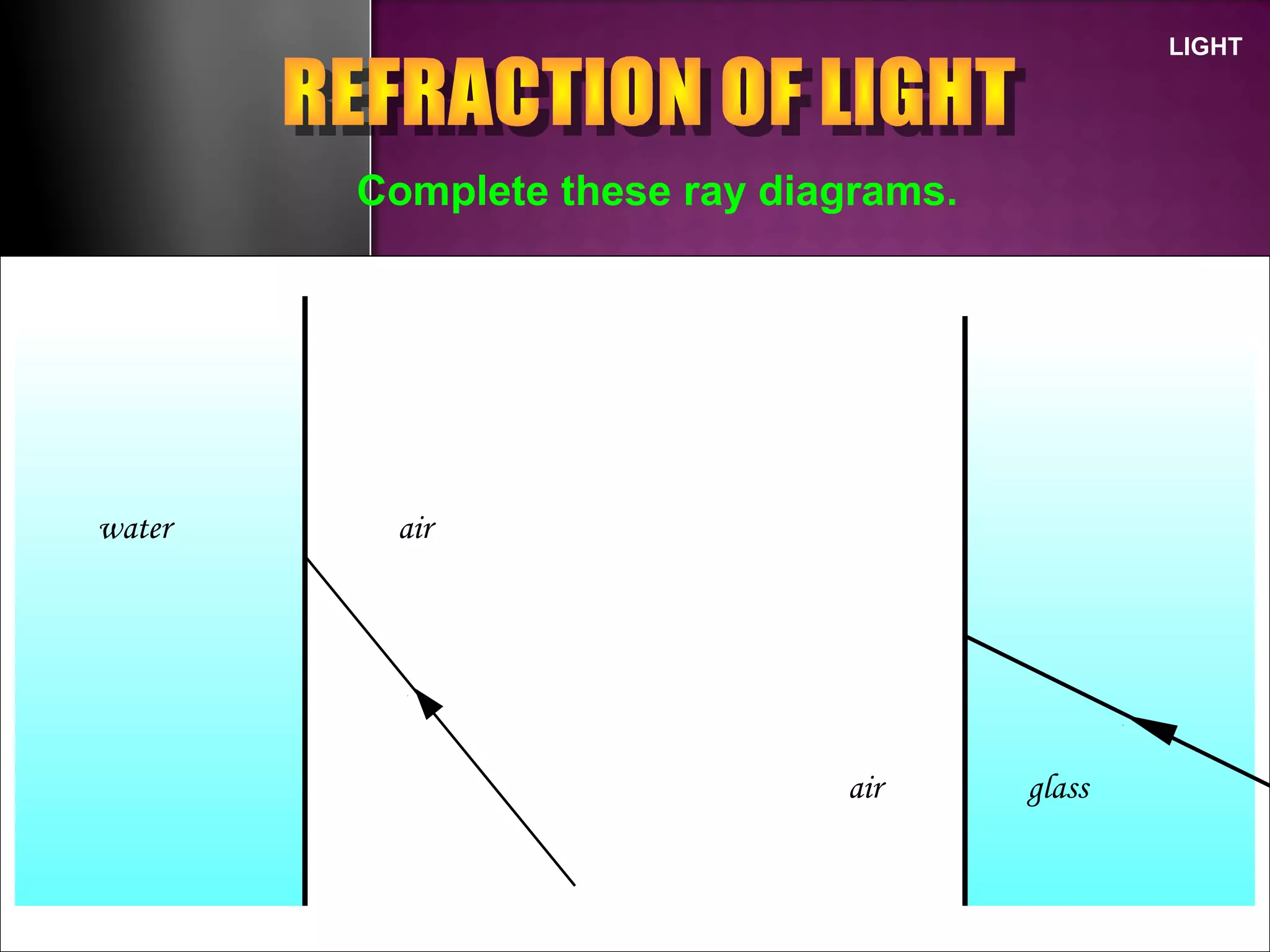
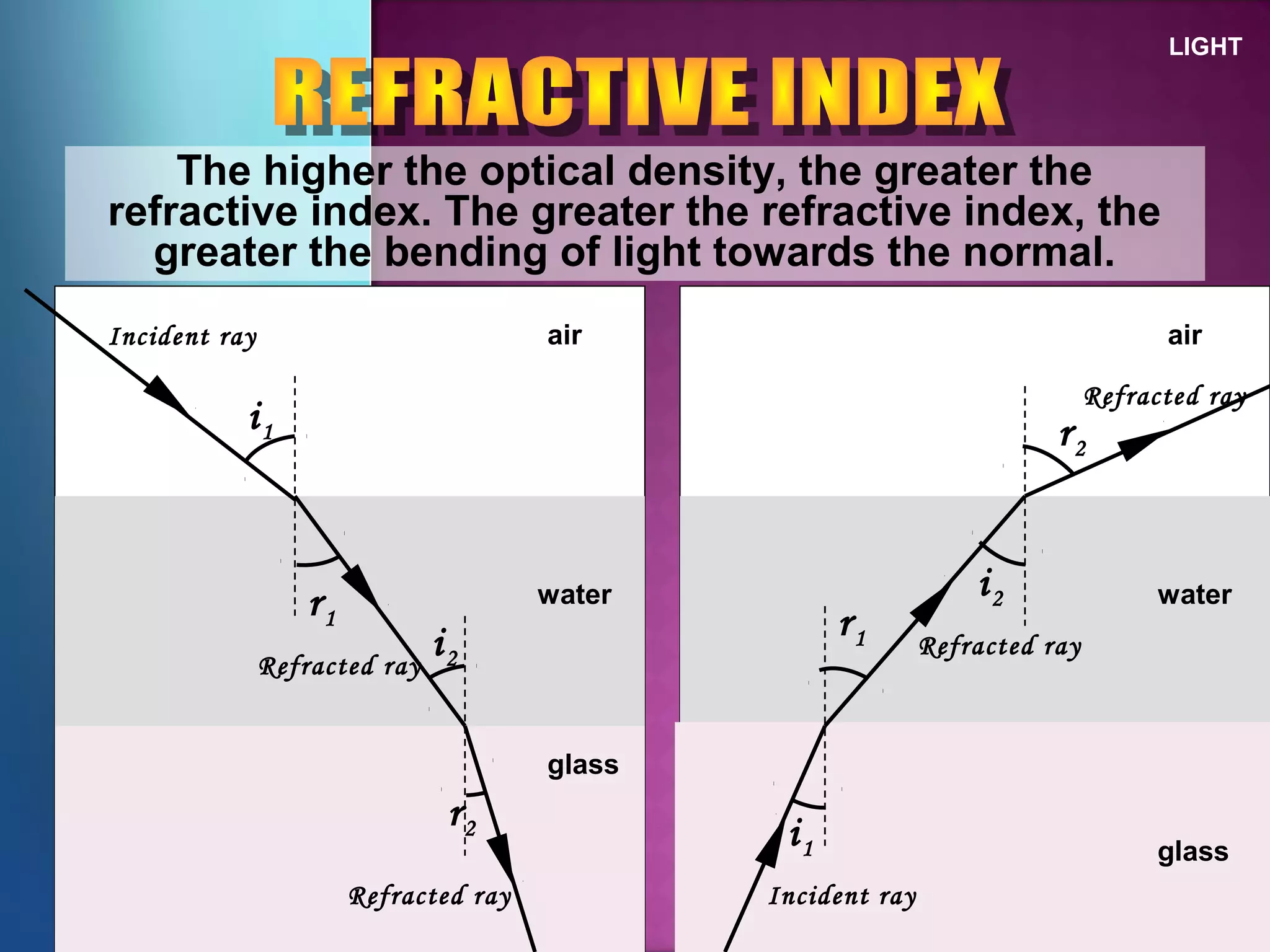
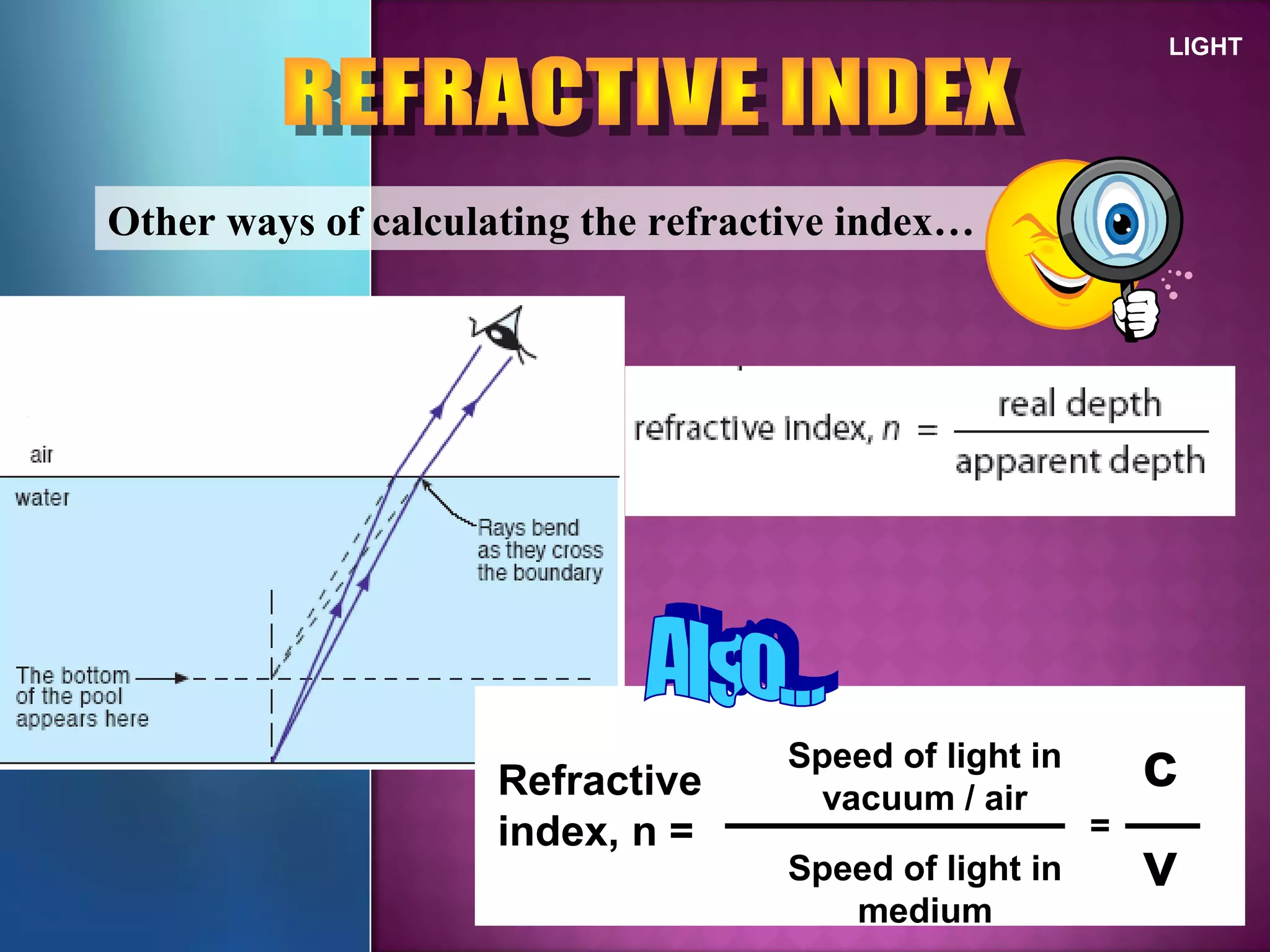
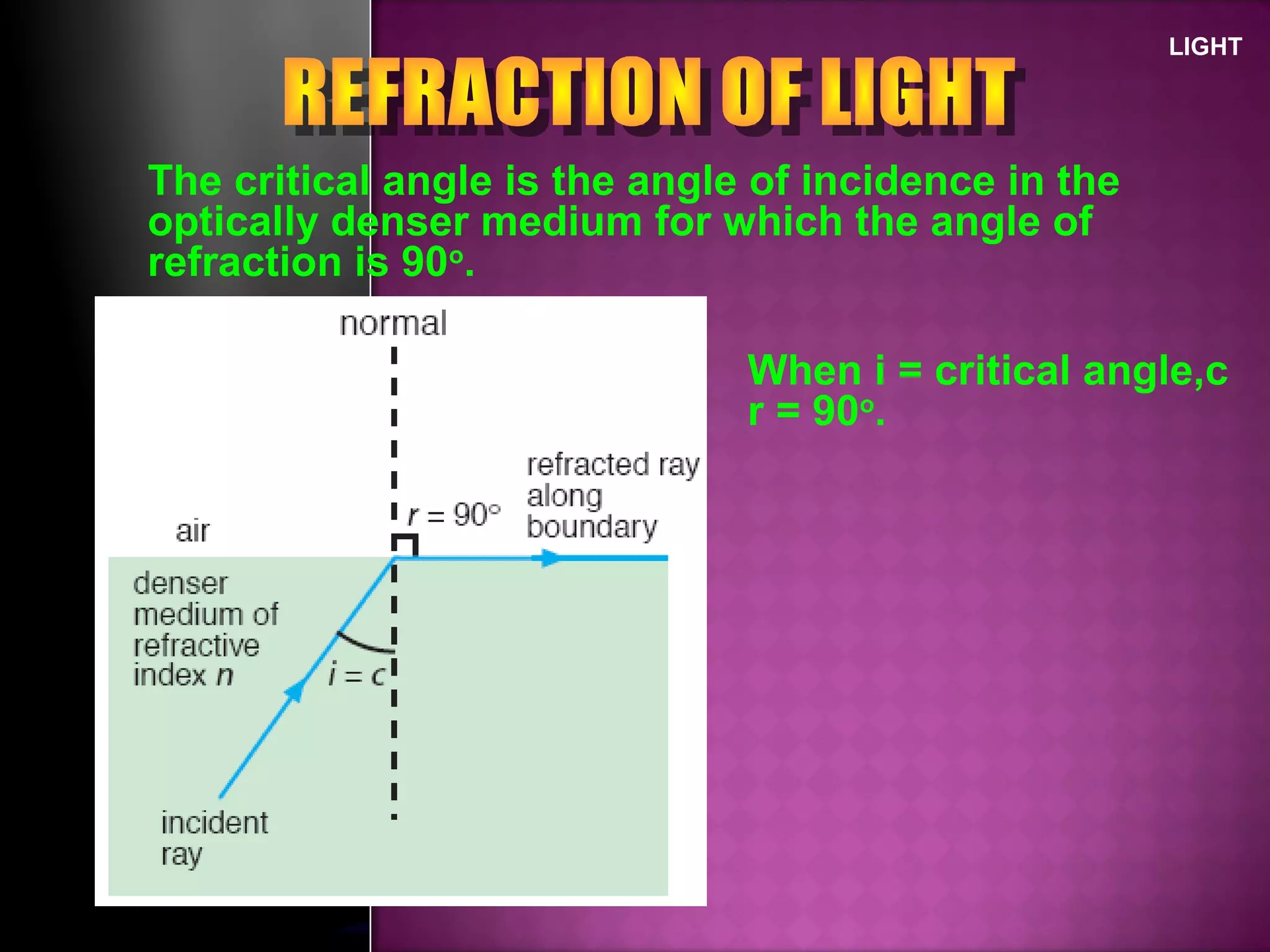
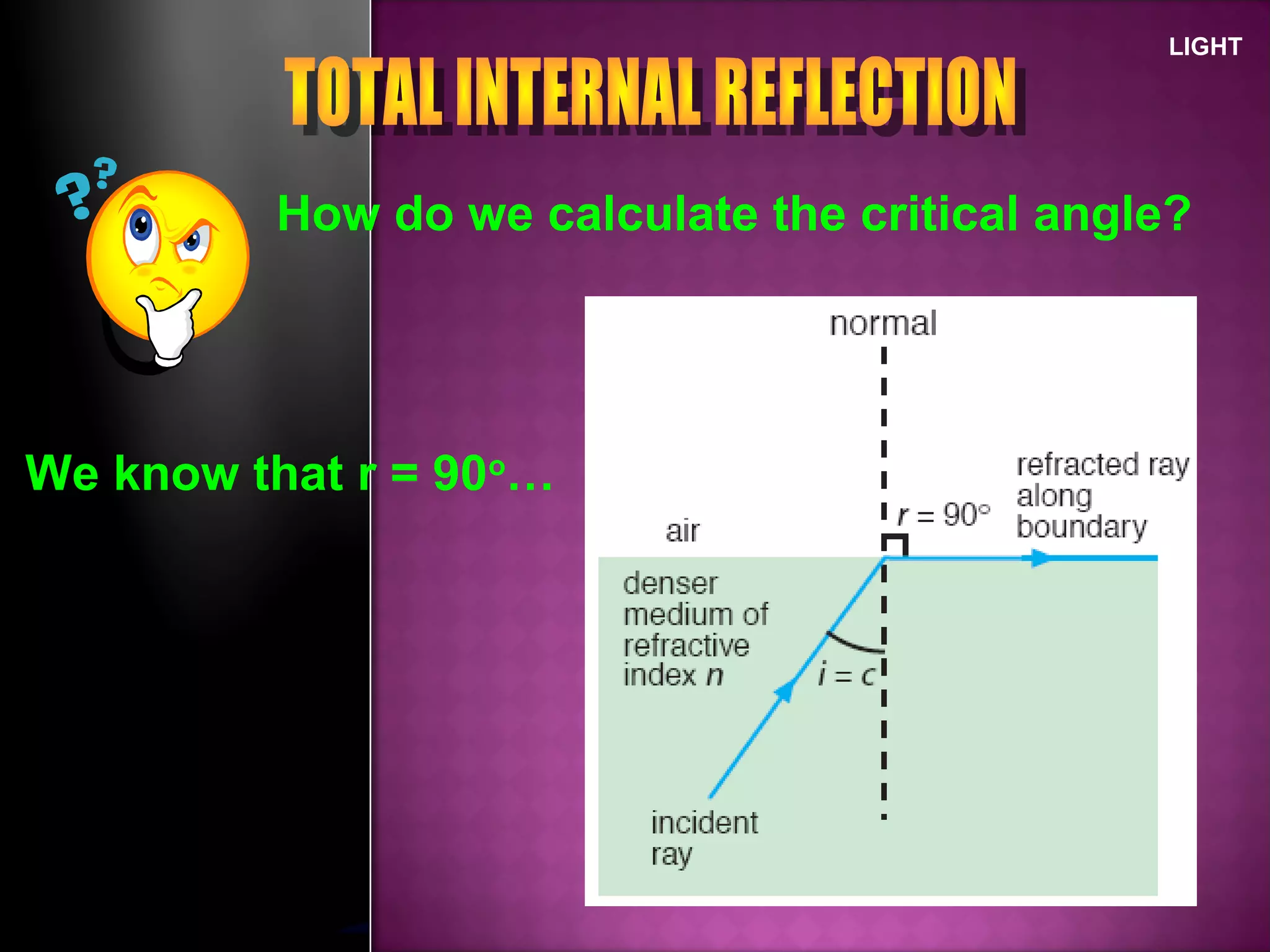
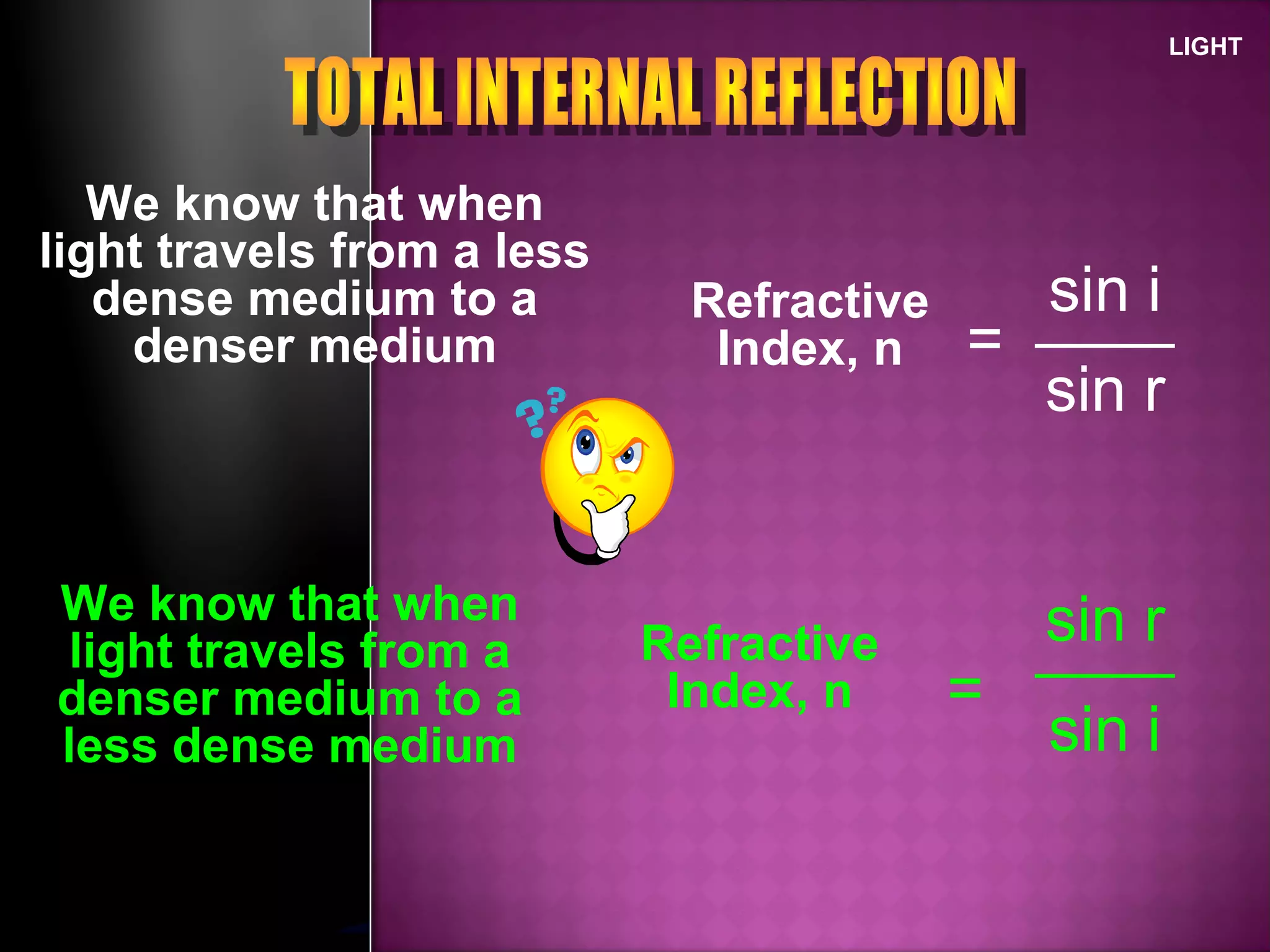
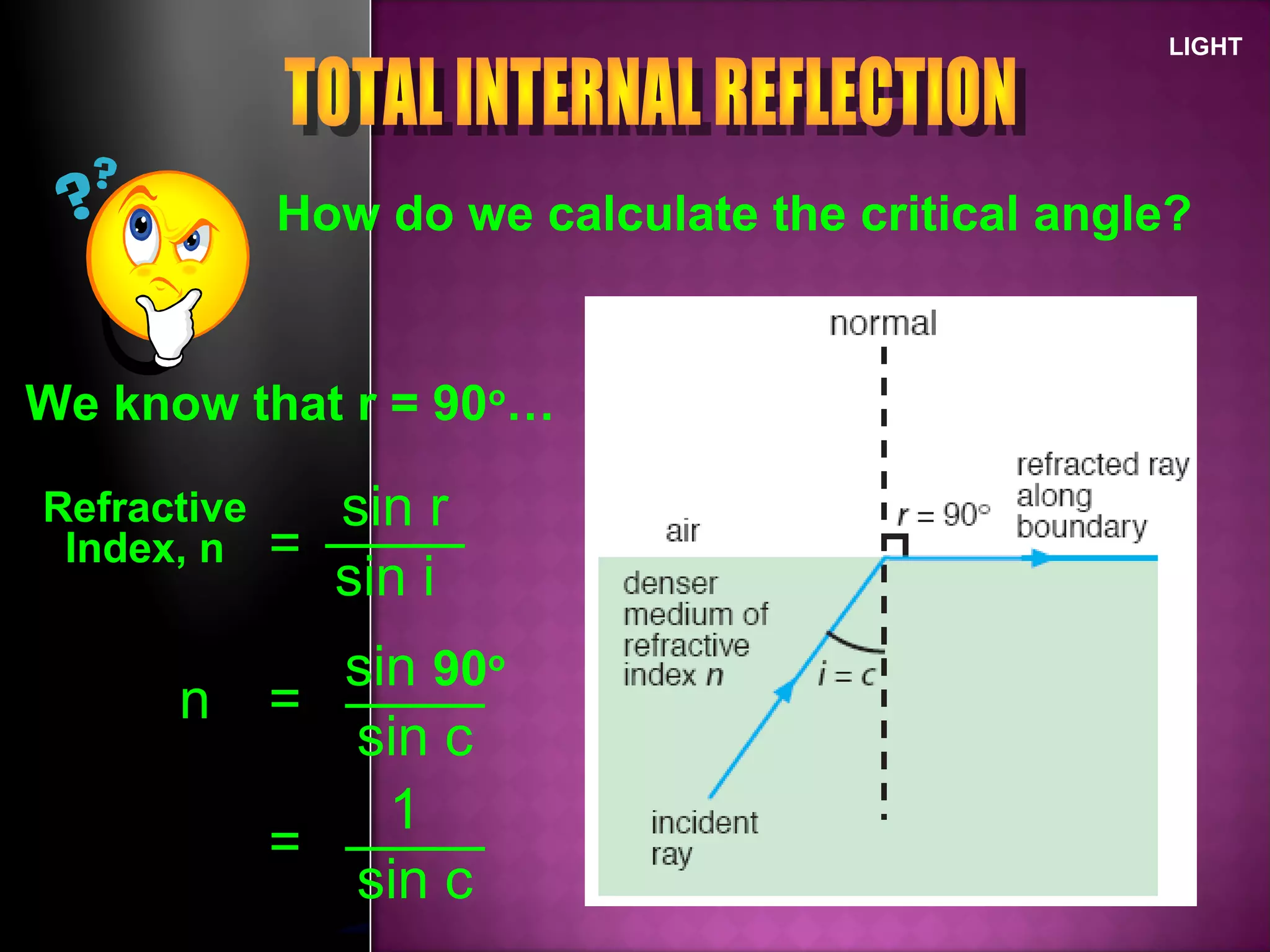
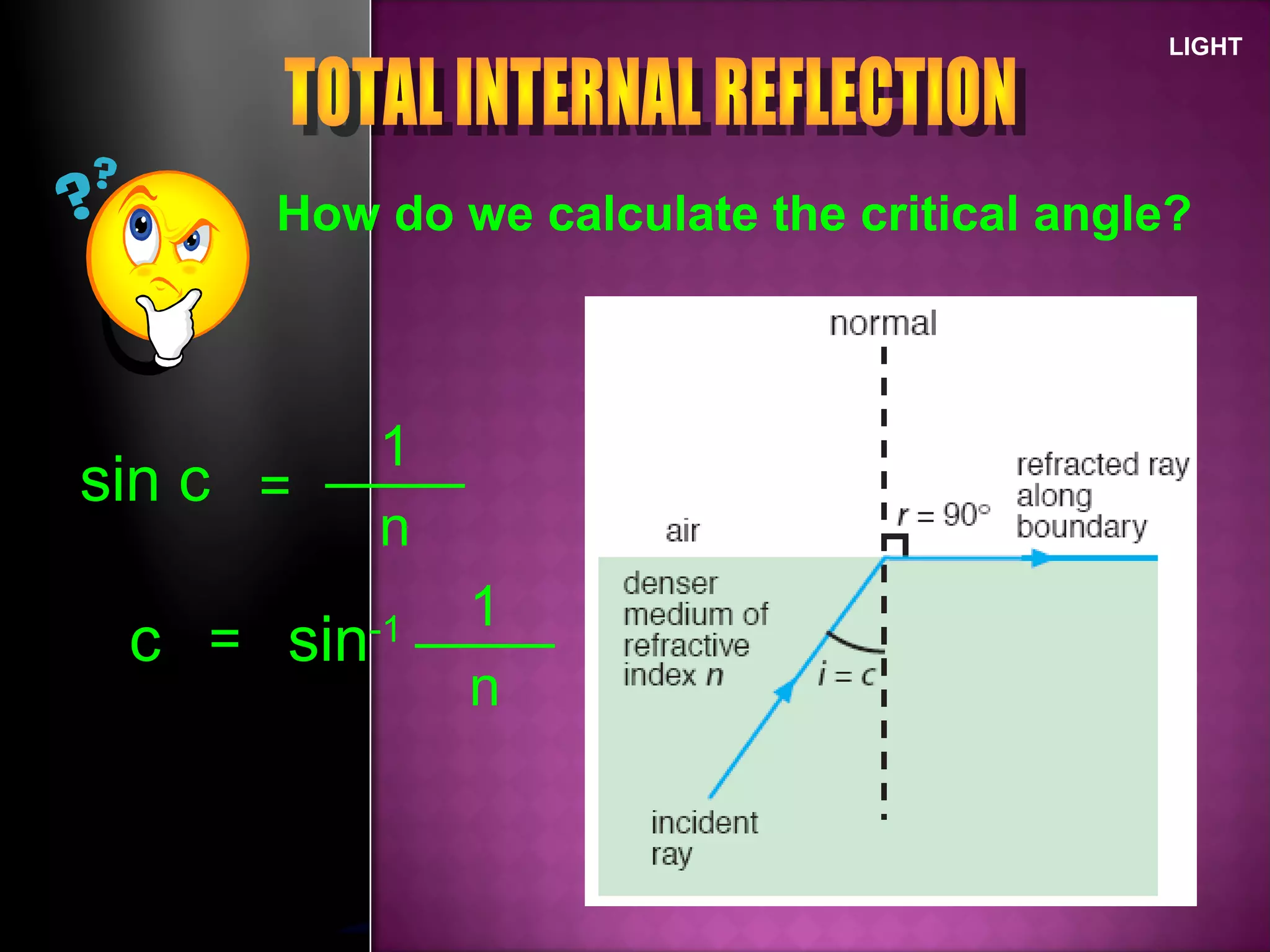
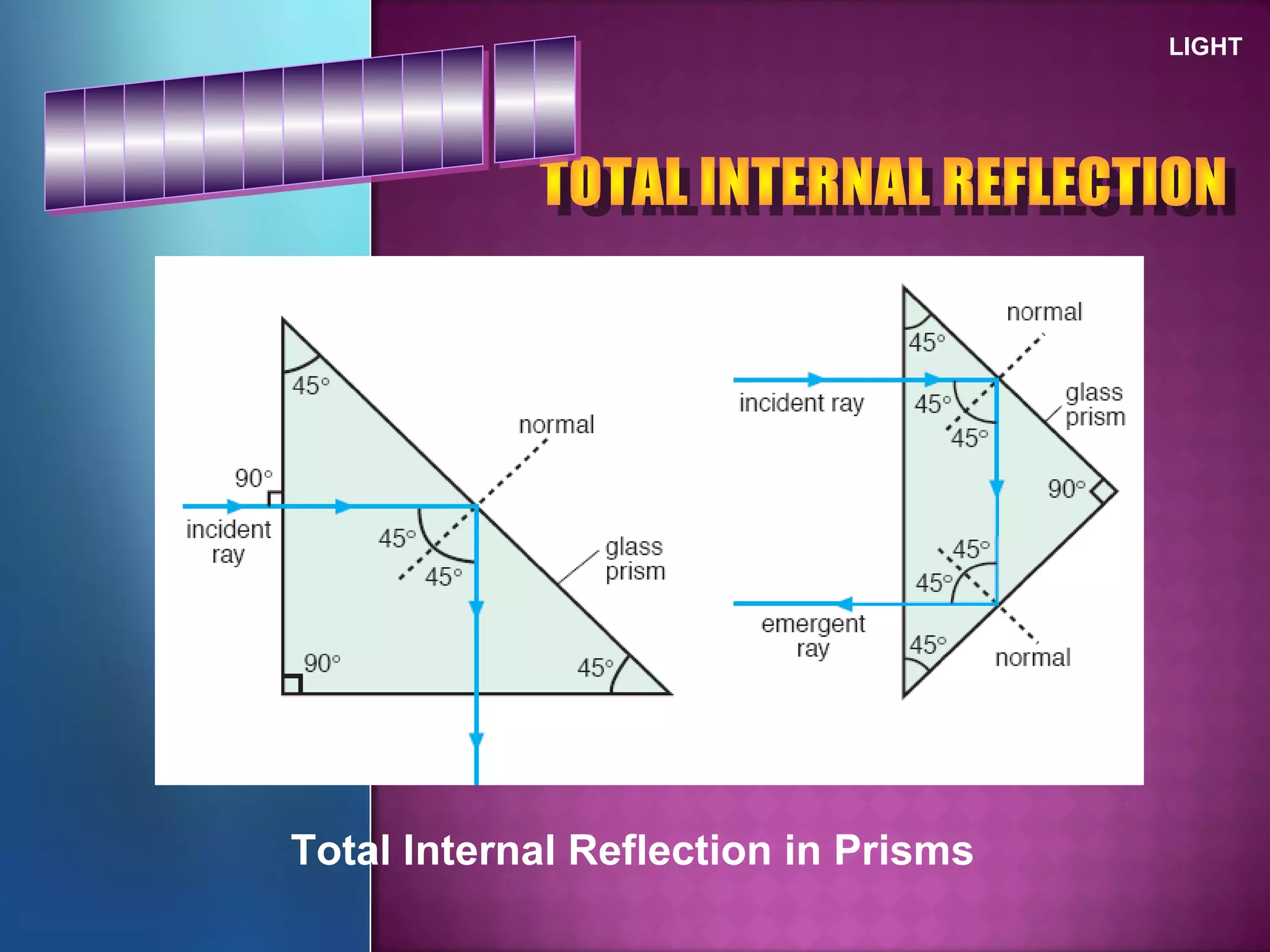
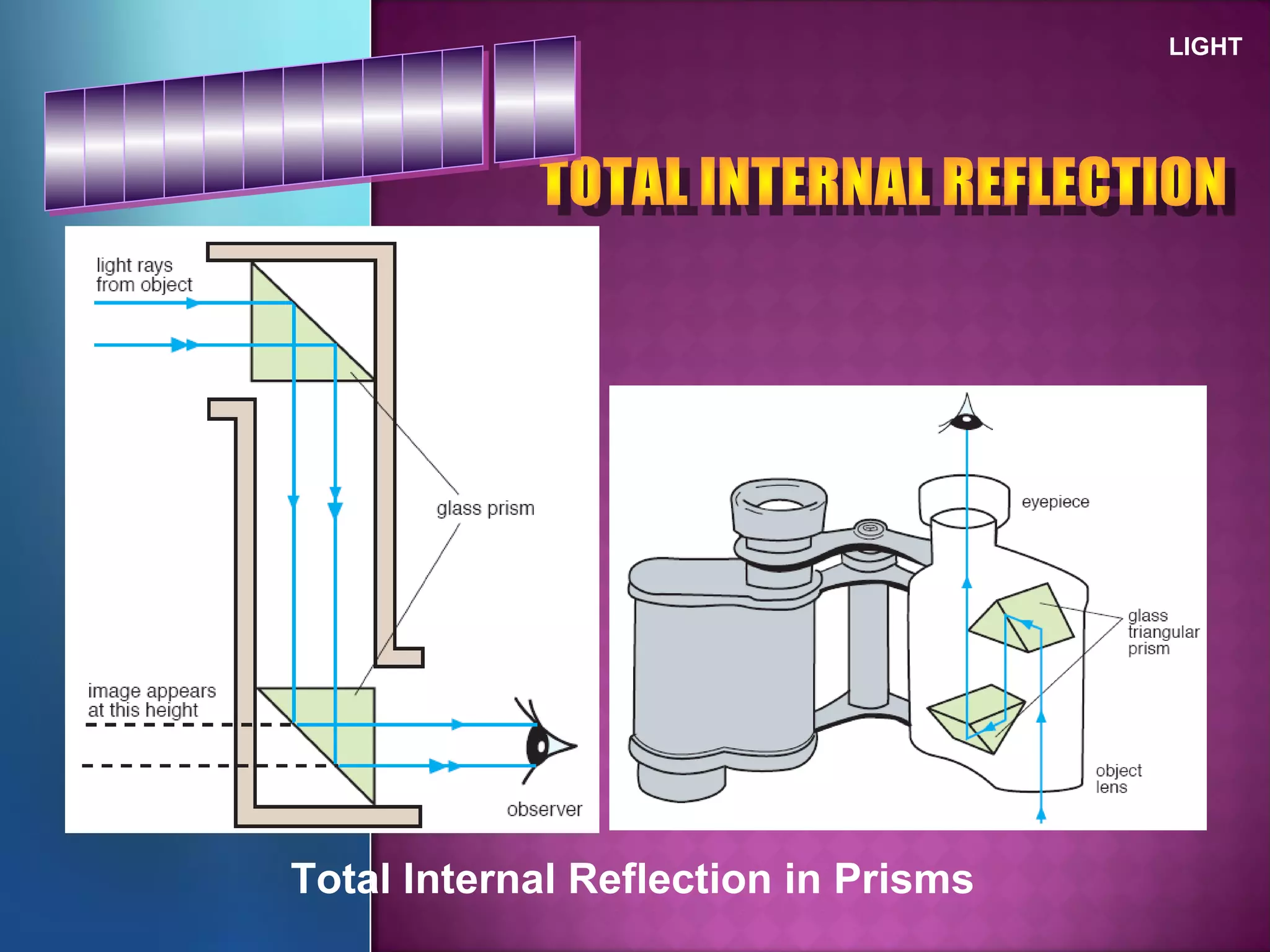
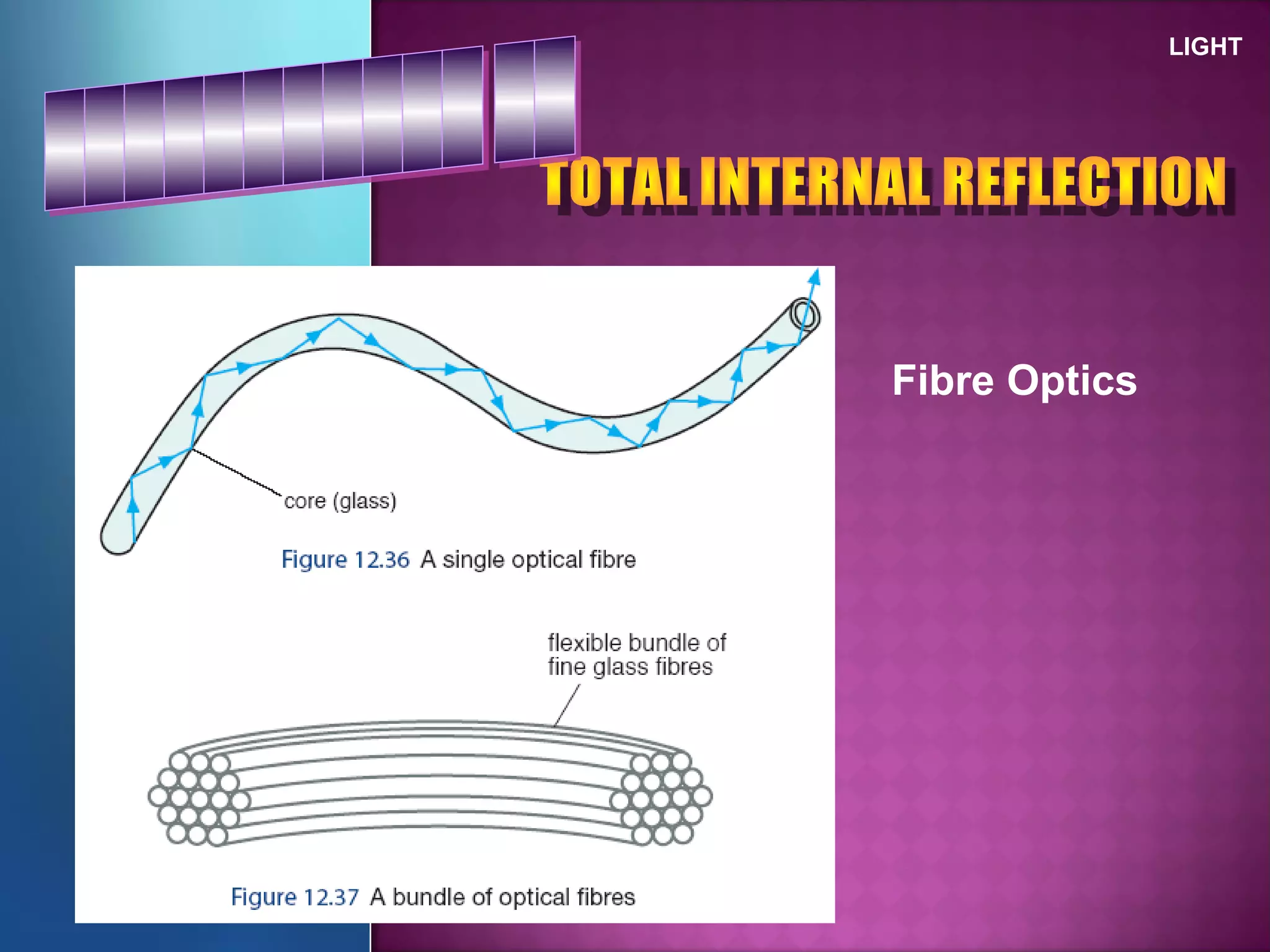
Refraction is the change in direction of light when it passes from one medium to another. Light bends towards the normal when traveling from a less dense to a more dense medium, and away from the normal in the opposite case. The ratio of sines of the angle of incidence and refraction is a constant called the refractive index, which depends on the optical densities of the media. Total internal reflection occurs when light travels from a denser to a less dense medium at an angle greater than the critical angle.