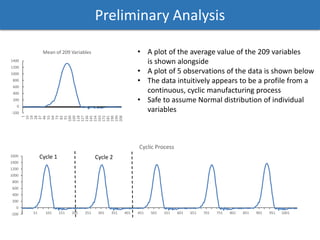
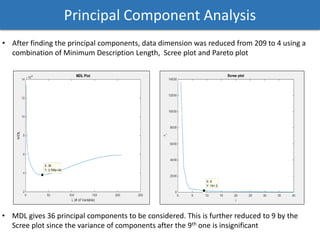
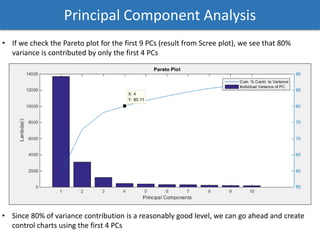
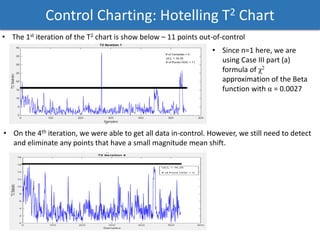
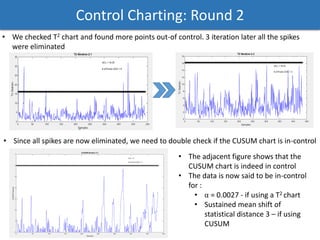
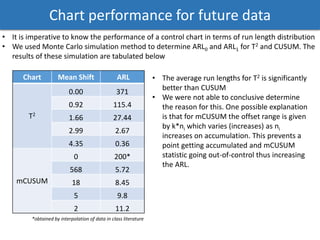
The document discusses a phased analysis of manufacturing process control, combining Hotelling's T2 and CUSUM methods. It details steps including data analysis, principal component analysis, and the development of control charts to detect out-of-control conditions. The findings indicate that Hotelling's T2 charts generally perform better in terms of average run length compared to CUSUM charts, though further iterations may be necessary for accuracy.

1. Phase I analysis for
manufacturing process control –
A combination of T2 and CUSUM
method
Authors –
Sandeep Nemmani
Vanshaj Handoo

2. Analysis approach
Preliminary
Analysis
• Identify the type of data – discrete/continuous
• Trend analysis on the data
• Identify the type of manufacturing process
Principal
Component
Analysis
• Use covariance matrix to convert original data into a new system of linearly
independent principal components
• Identify principal components contributing to about 80% of total variance using
description length, Scree plot and Pareto plot
Control
Charting
• Perform iterations of Hotelling T2 to remove spike type of change and m-CUSUM to
remove a sustained mean shift of statistical distance 3
• Find the in-control parameters - µ0 and Σ0
Chart
Performance
• Use Monte Carlo simulation method to determine the Run Length distribution for
both the T2 and the CUSUM charts

3. Preliminary Analysis
-200
0
200
400
600
800
1000
1200
1400
1
10
19
28
37
46
55
64
73
82
91
100
109
118
127
136
145
154
163
172
181
190
199
208
Mean of 209 Variables • A plot of the average value of the 209 variables
is shown alongside
• A plot of 5 observations of the data is shown below
• The data intuitively appears to be a profile from a
continuous, cyclic manufacturing process
• Safe to assume Normal distribution of individual
variables
-200
0
200
400
600
800
1000
1200
1400
1600
1 51 101 151 201 251 301 351 401 451 501 551 601 651 701 751 801 851 901 951 1001
Cyclic Process
Cycle 1 Cycle 2

4. Principal Component Analysis
• After finding the principal components, data dimension was reduced from 209 to 4 using a
combination of Minimum Description Length, Scree plot and Pareto plot
• MDL gives 36 principal components to be considered. This is further reduced to 9 by the
Scree plot since the variance of components after the 9th one is insignificant

5. Principal Component Analysis
• If we check the Pareto plot for the first 9 PCs (result from Scree plot), we see that 80%
variance is contributed by only the first 4 PCs
• Since 80% of variance contribution is a reasonably good level, we can go ahead and create
control charts using the first 4 PCs

6. Control Charting: Hotelling T2 Chart
• The 1st iteration of the T2 chart is show below – 11 points out-of-control
• On the 4th iteration, we were able to get all data in-control. However, we still need to detect
and eliminate any points that have a small magnitude mean shift.
• Since n=1 here, we are
using Case III part (a)
formula of χ2
approximation of the Beta
function with α = 0.0027

7. Control Charting: m-CUSUM Chart
• After eliminating all spikes, we use the CUSUM method to eliminate sustained mean shift
• After 6 iterations of the CUSUM chart, we were ale to eliminate all points having a mean shift
of statistical distance 3
• We tried to detect a mean shift of statistical
distance 3
• In the adjacent figure, we see a large number
of points going out-of-control indicating that
a sustained mean shift did exist and
remained undetected by the T2 chart
• UCL is determined by interpolation of data in
literature
• We cannot, however, stop at this
point an state the remaining data
points are all in control
• To make such a statement we
need both the, T2 and the
CUSUM charts to be in control at
the same time
• Hence, the need to check T2
again

8. Control Charting: Round 2
• We checked T2 chart and found more points out-of control. 3 iteration later all the spikes
were eliminated
• Since all spikes are now eliminated, we need to double check if the CUSUM chart is in-control
• The adjacent figure shows that the
CUSUM chart is indeed in control
• The data is now said to be in-control
for :
• α = 0.0027 - if using a T2 chart
• Sustained mean shift of
statistical distance 3 – if using
CUSUM

9. Chart performance for future data
• It is imperative to know the performance of a control chart in terms of run length distribution
• We used Monte Carlo simulation method to determine ARL0 and ARL1 for T2 and CUSUM. The
results of these simulation are tabulated below
Chart Mean Shift ARL
T2
0.00 371
0.92 115.4
1.66 27.44
2.99 2.67
4.35 0.36
mCUSUM
0 200*
568 5.72
18 8.45
5 9.8
2 11.2
• The average run lengths for T2 is significantly
better than CUSUM
• We were not able to conclusive determine
the reason for this. One possible explanation
is that for mCUSUM the offset range is given
by k*ni which varies (increases) as ni
increases on accumulation. This prevents a
point getting accumulated and mCUSUM
statistic going out-of-control thus increasing
the ARL.
*obtained by interpolation of data in class literature

10. Key learning
• Owing to large dimensionality of data, it is difficult to select a particular approach for setting
up a process control detection method. Using multiple univariate charts for each variable is
out of question. The question then is to either use a multivariate chart like Hotelling T2 or
CUSUM chart or individual Shewhart charts for un-correlated principal components. In our
approach we have not selected the individual charts for principal components because a
process may be out of control even when the individual charts are in control. A T2 or CUSUM
chart is thus more definitive in terms of its response.
• Even after determining the charts that we use it is important to determine the order of use
since that can reduce the number iterations to get the in-control data. Doing CUSUM before
T2 would have saved some iterations.
• The Average run length distributions for T2 are better than m-CUSUM. We were not able to
conclusive determine the reason for this. One possible explanation is that for m-CUSUM the
offset range is given by k*ni which varies (increases) as ni increases on accumulation. This
prevents a point getting accumulated and m-CUSUM statistic going out-of-control thus
increasing the ARL.