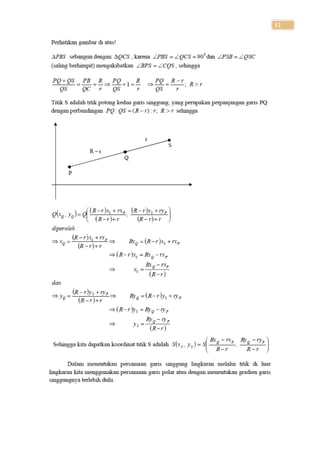
Dokumen tersebut membahas tentang lingkaran dan hubungannya dengan garis. Dijelaskan bahwa lingkaran terdiri dari pusat dan keliling, serta memiliki persamaan matematis berdasarkan pusat dan jari-jari. Garis dapat memotong, menyentuh, atau tidak beririsan dengan lingkaran, dengan aturan-aturan khusus untuk garis singgung dan hubungan antar dua lingkaran.