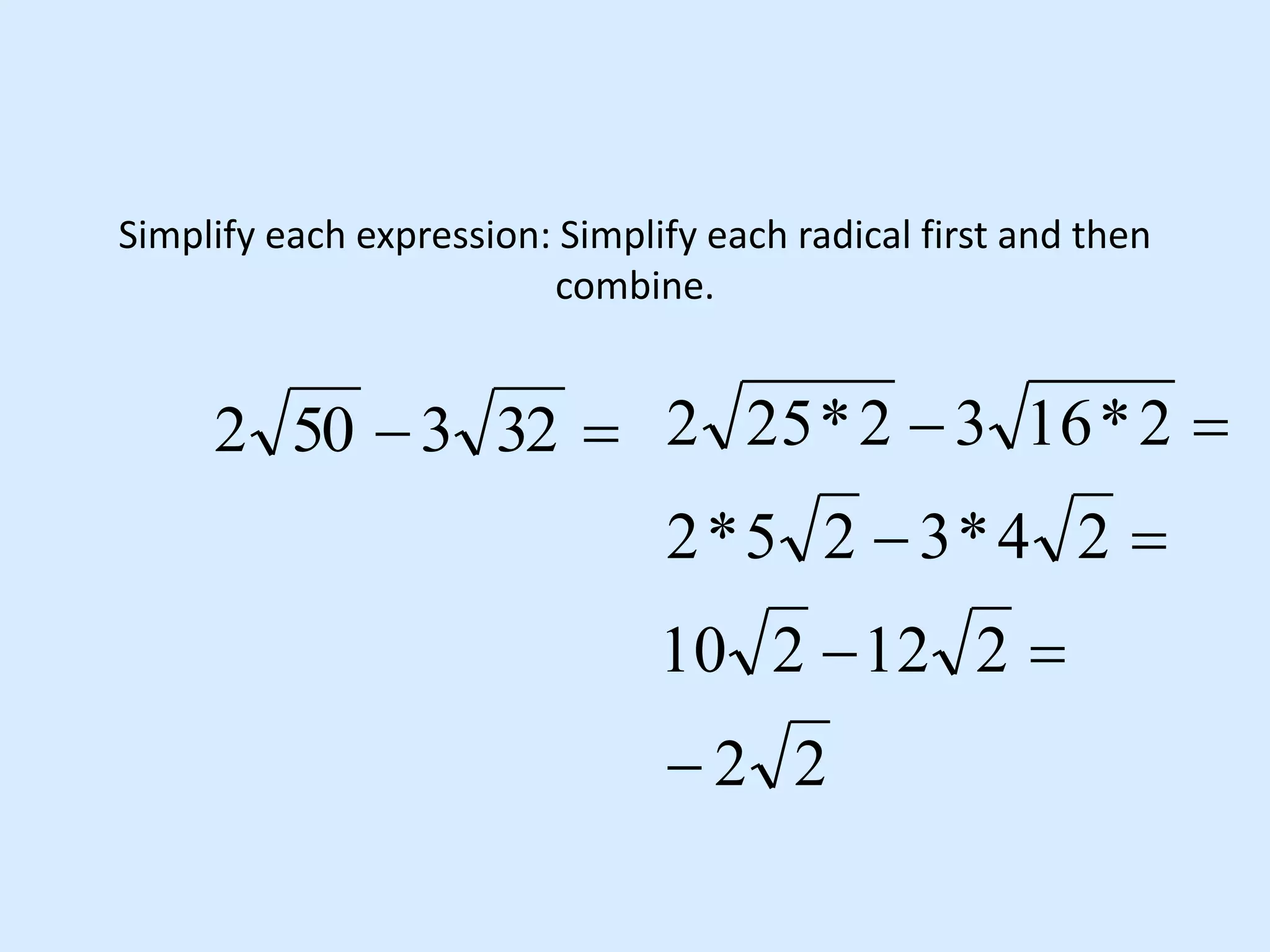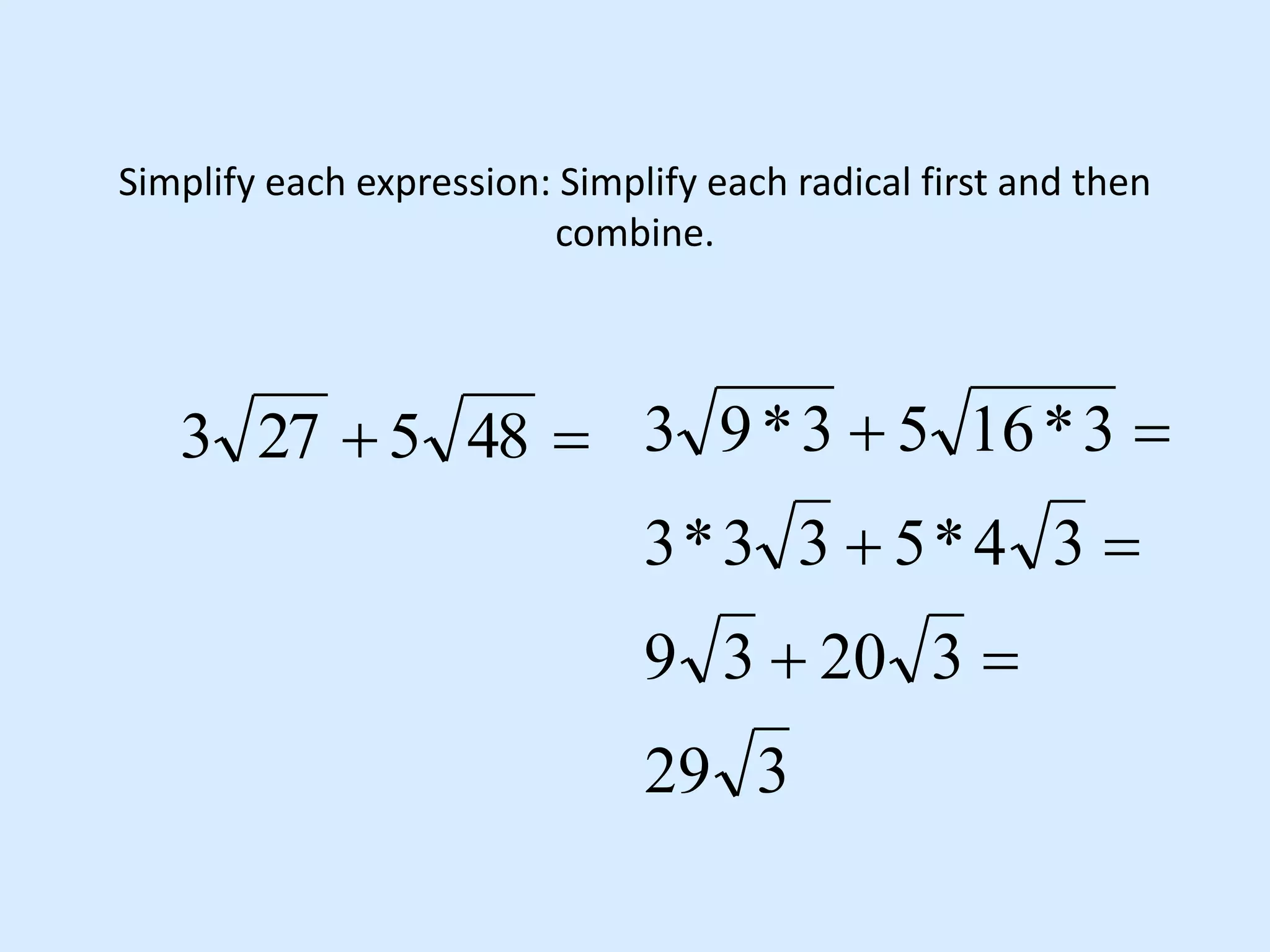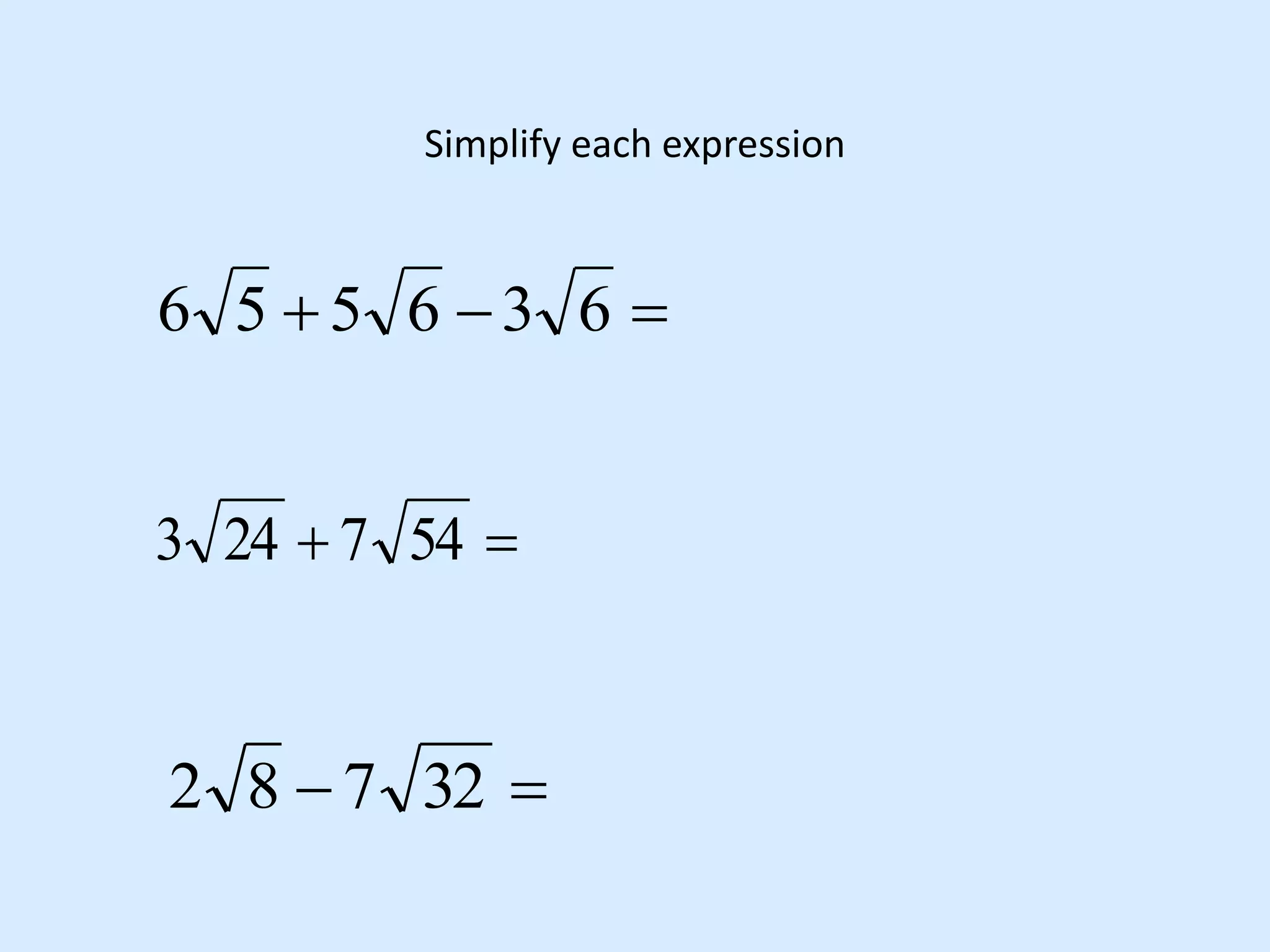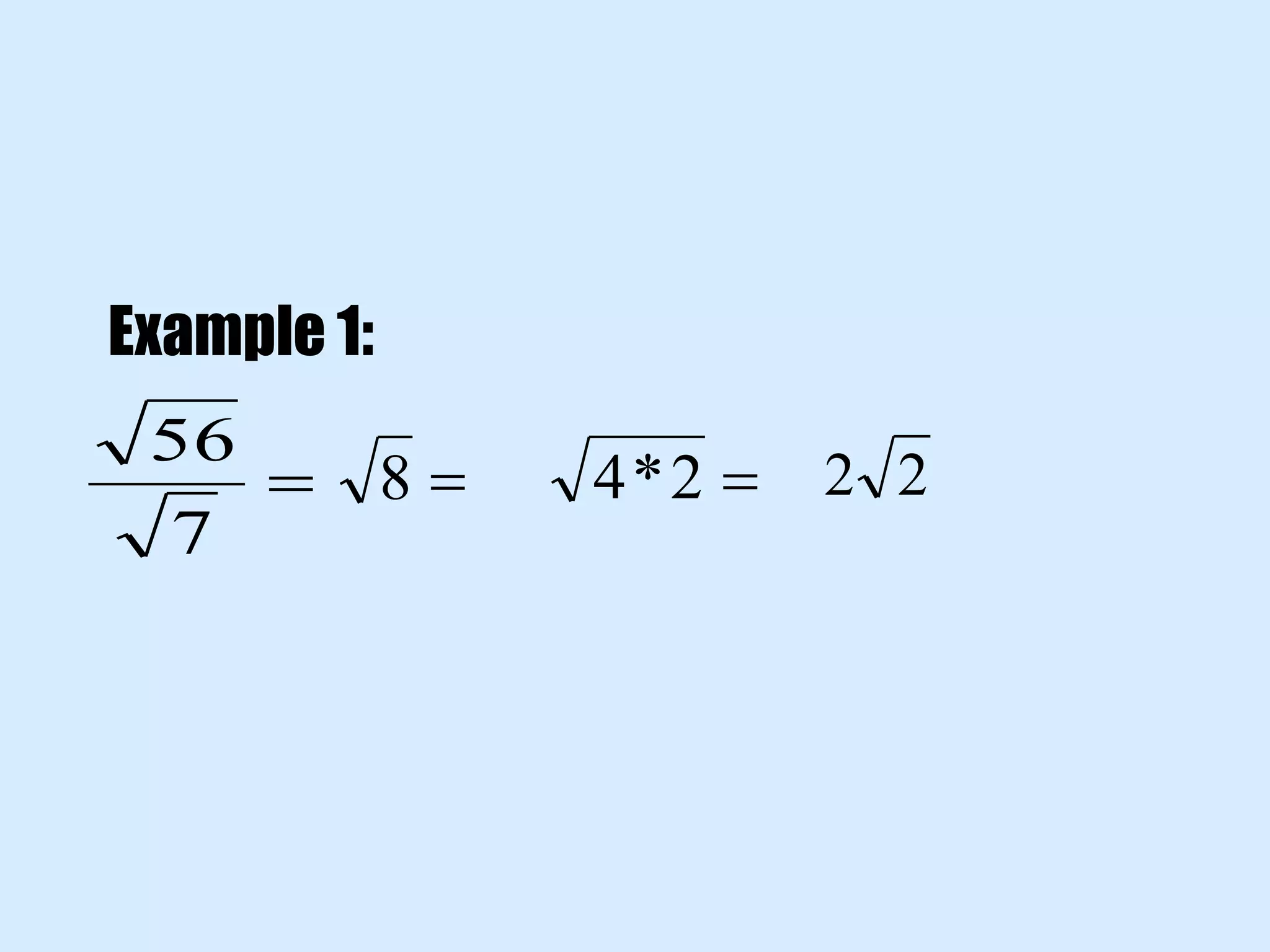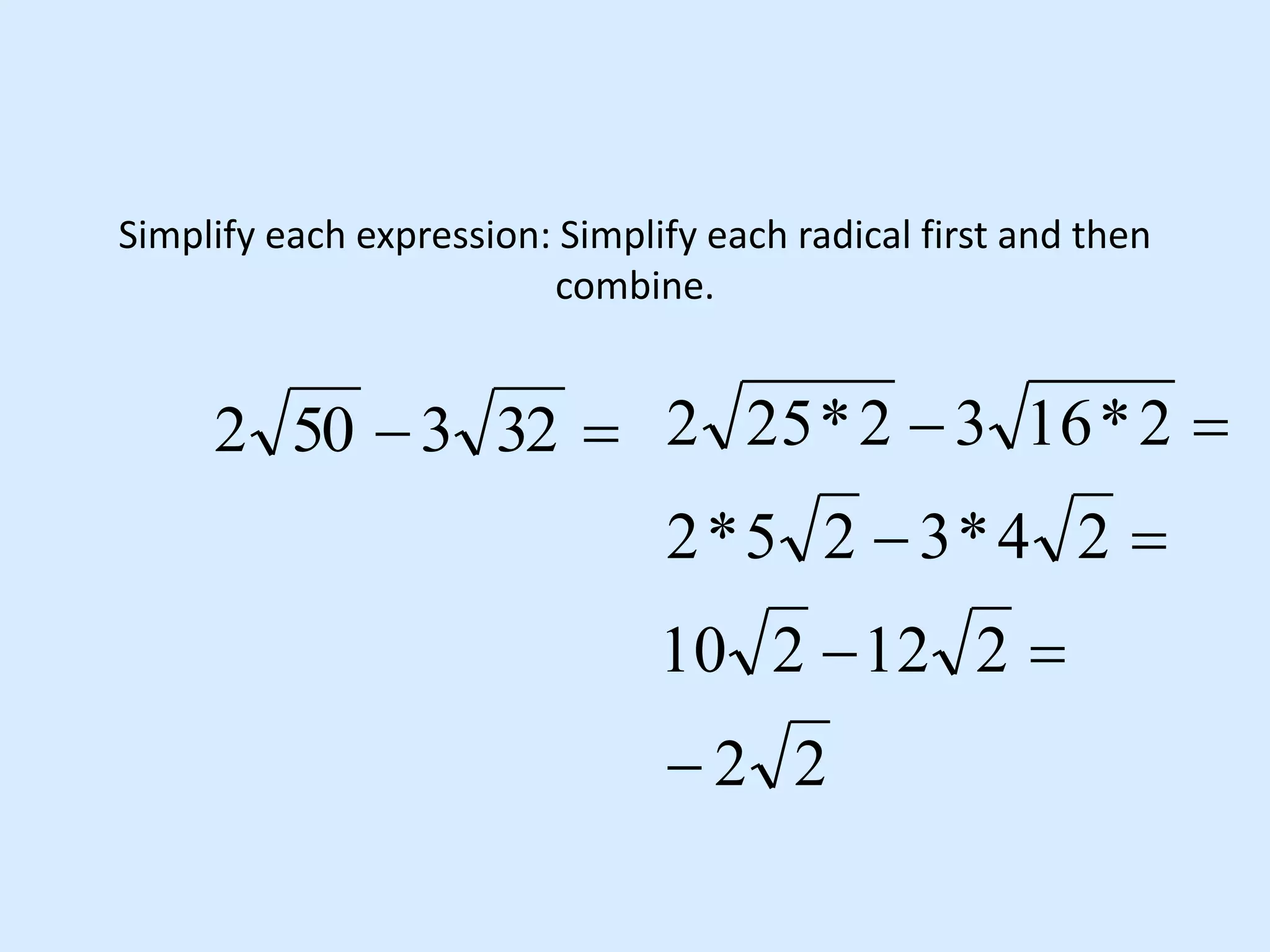
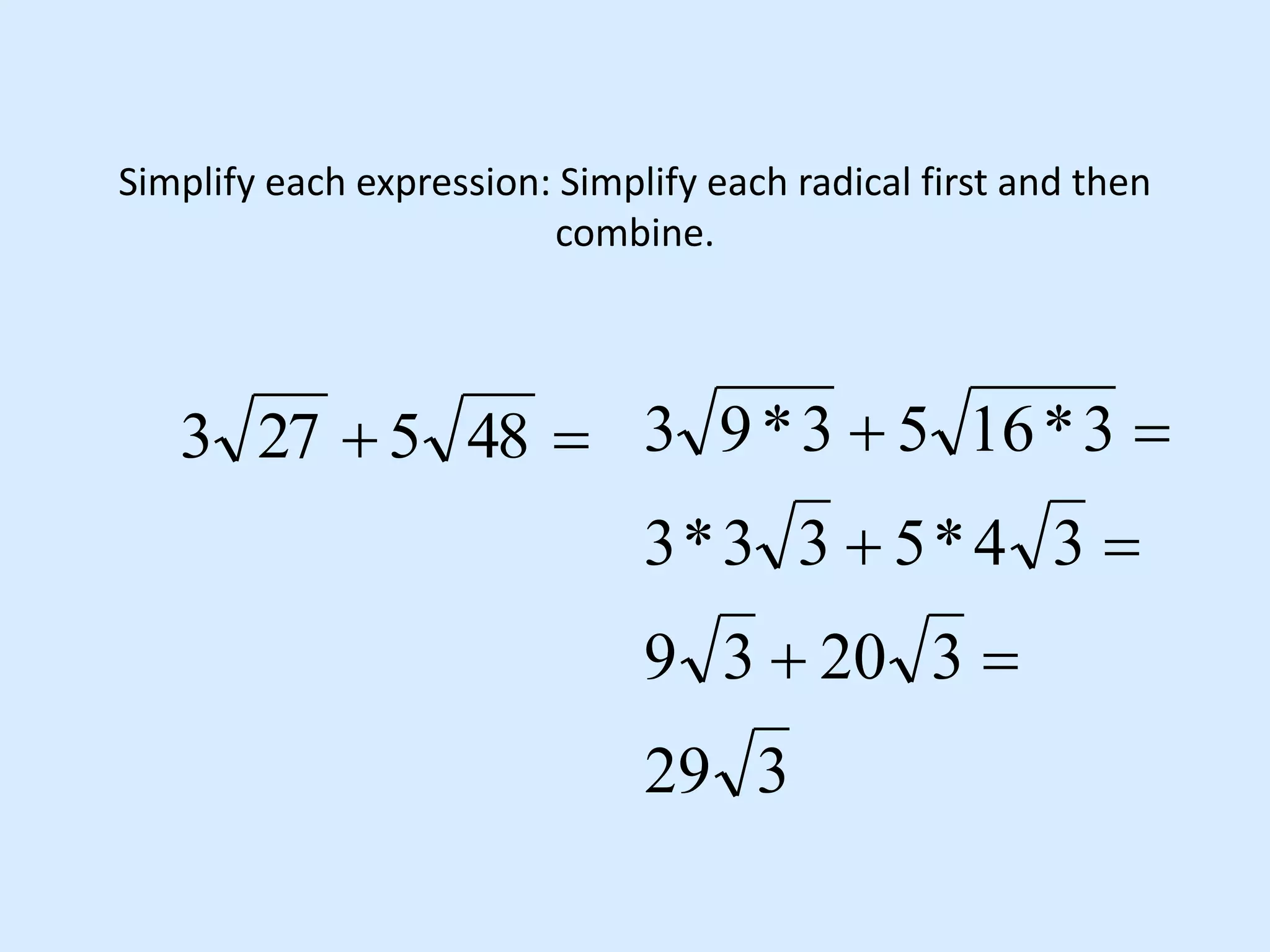
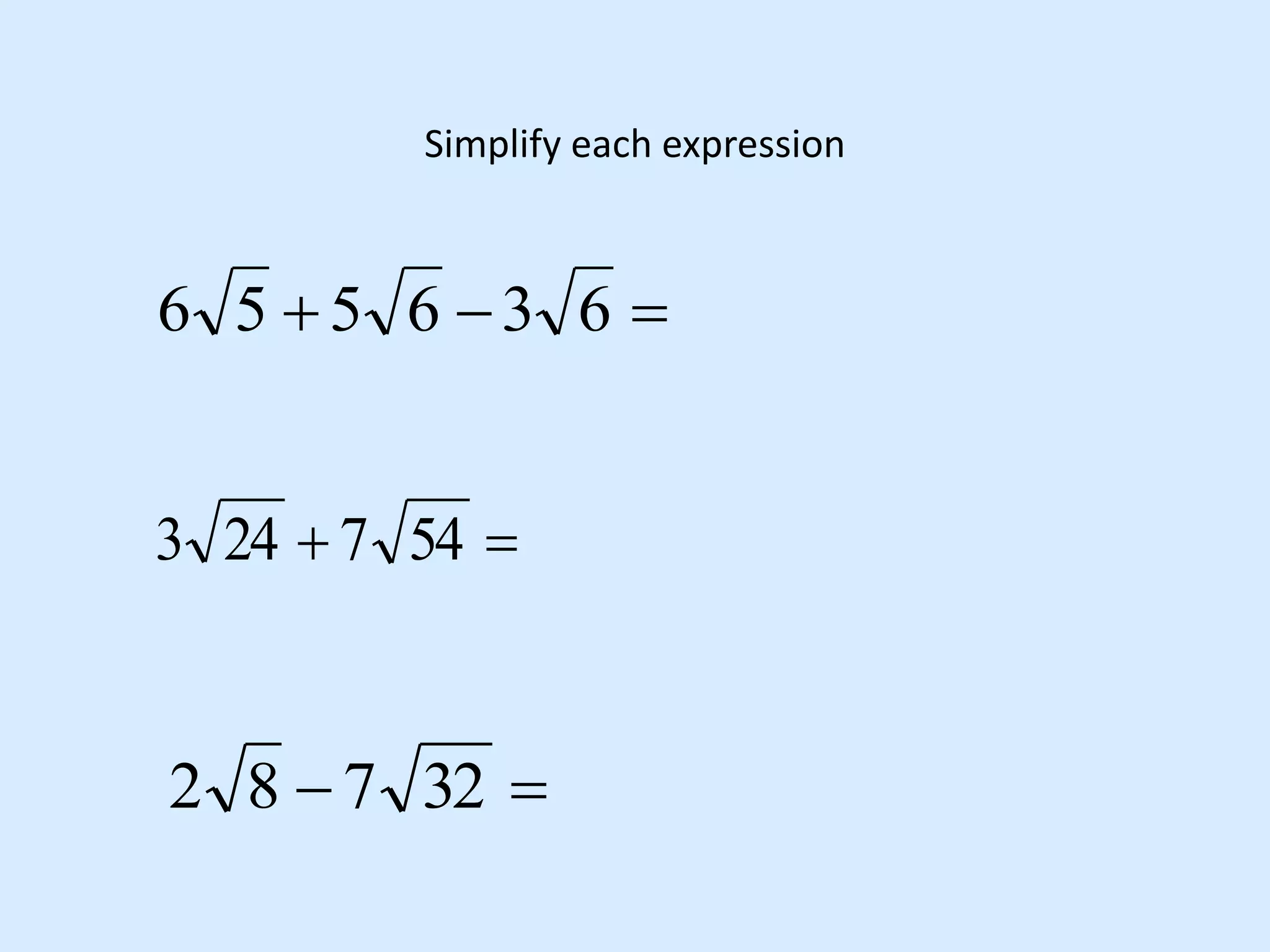
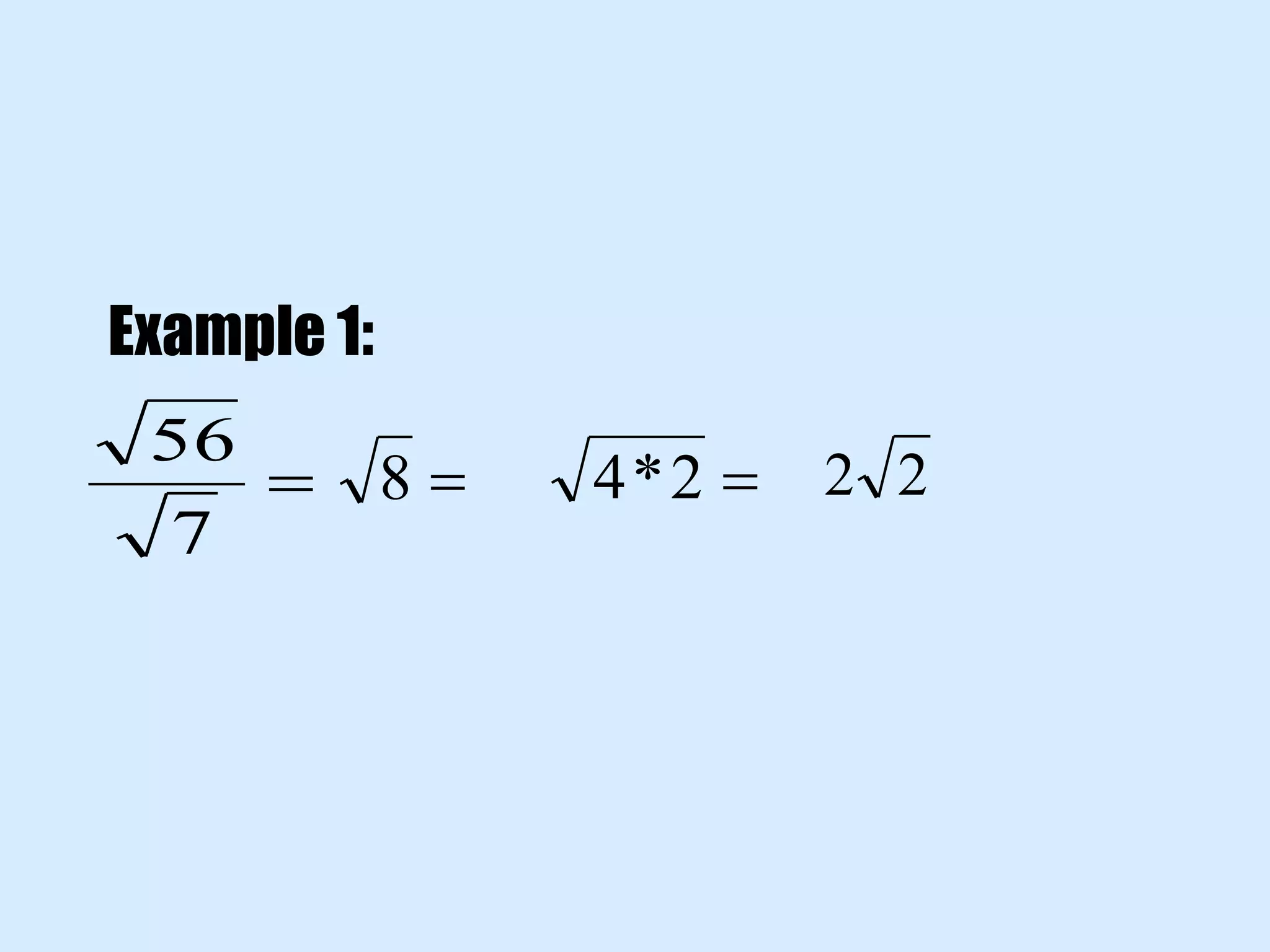
This document discusses operations with radicals. It covers multiplying radicals by combining like terms, dividing radicals by dividing coefficients and radicands when possible and rationalizing denominators to remove radicals, and FOILing with radicals by using the rules for multiplying and adding/subtracting. Examples are provided for simplifying expressions with radicals and for rationalizing denominators when dividing radicals.

1. Operations with Radicals

2. Multiplying Radicals
•
•
•

3. +
To combine radicals: combine
the coefficients of like radicals

4. Simplify each expression
 737576 78
 62747365 7763 

5. Simplify each expression: Simplify each radical first and then
combine.
 323502
22
212210
24*325*2
2*1632*252





6. Simplify each expression: Simplify each radical first and then
combine.
 485273
329
32039
34*533*3
3*1653*93




7. Simplify each expression
 636556
 547243
 32782

8. Simplify each expression
 20556
 32718
 6367282

9. FOIL with Radicals
• Use rules for multiplying and add/subtract
• Ex: (3 + 5)( 5 − 4)

11. To divide radicals:
divide the coefficients,
divide the radicands if
possible, and
rationalize the
denominator so that
no radical remains in
the denominator

12. 
7
56
8 2*4 22
Example 1:

13. 
7
6
This cannot be
divided which leaves
the radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

7
7
*
7
6

49
42
7
42
42 cannot be
simplified, so we are
finished.
Example 2:

14. This can be divided
which leaves the
radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

10
5

2
2
*
2
1
2
2
Example 3:

15. This cannot be
divided which leaves
the radical in the
denominator. We do
not leave radicals in
the denominator. So
we need to
rationalize by
multiplying the
fraction by something
so we can eliminate
the radical in the
denominator.

12
3

3
3
*
32
3

9*2
33

6
33
2
3Reduce
the
fraction.
Example 4: