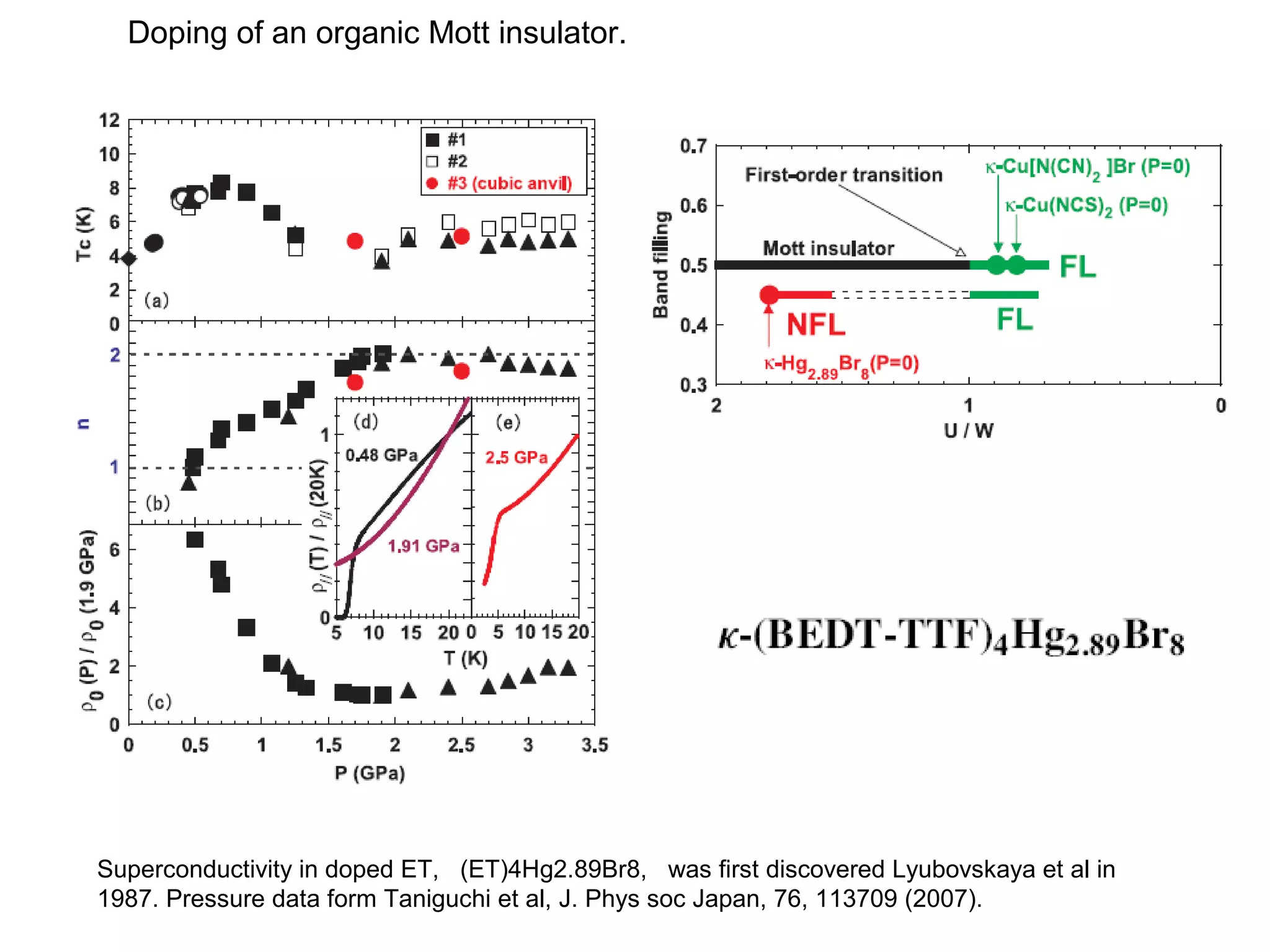
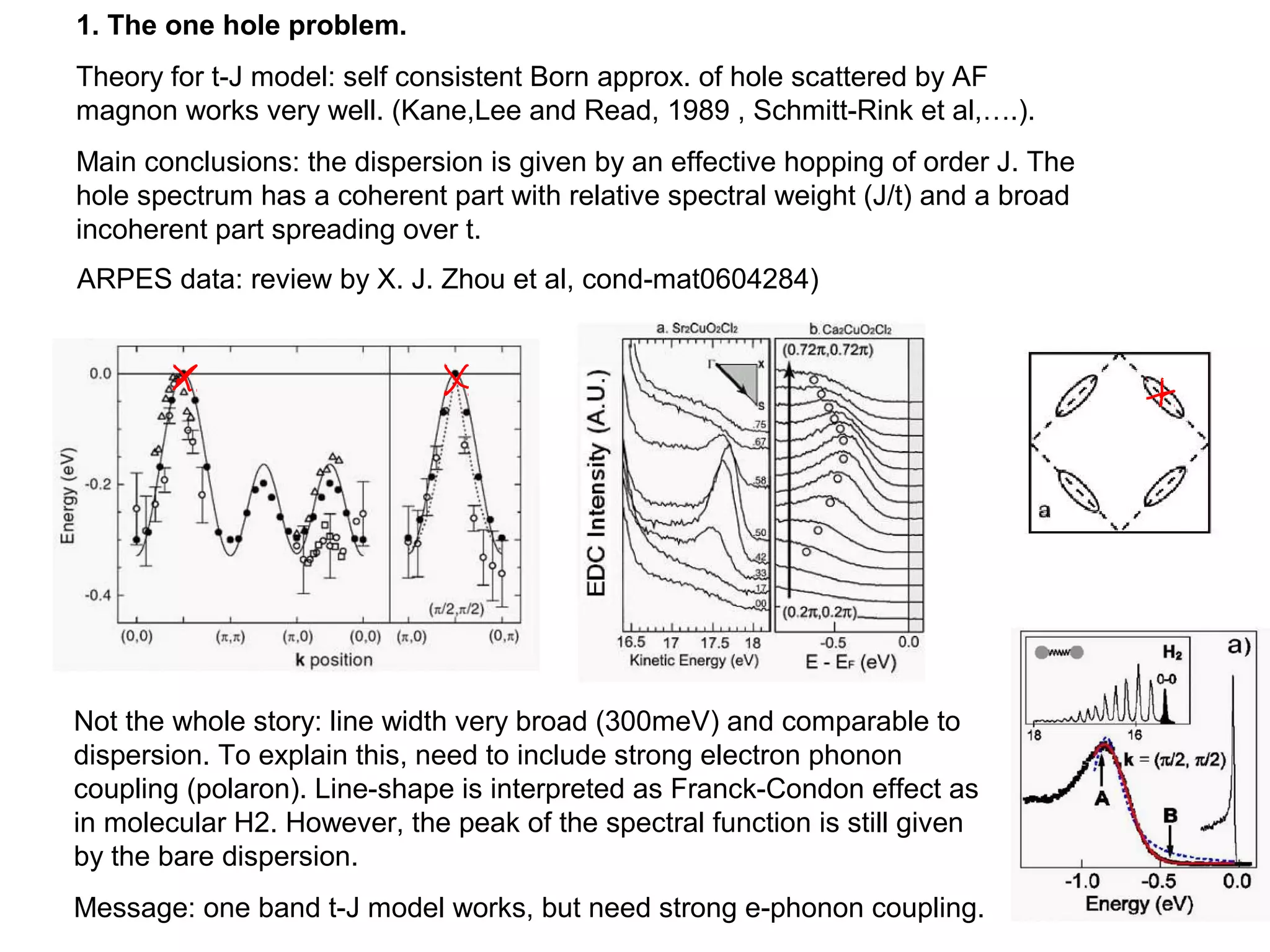
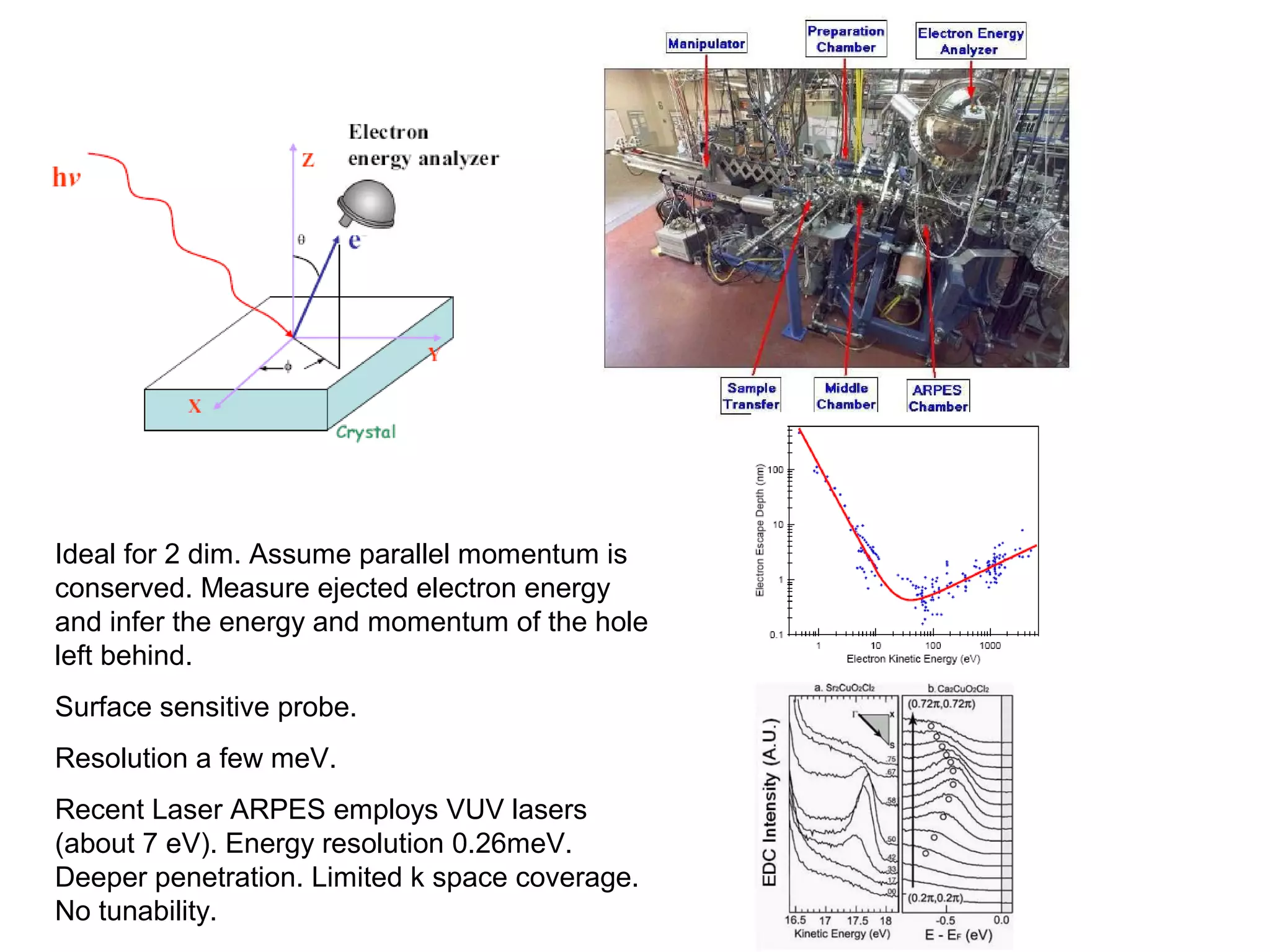
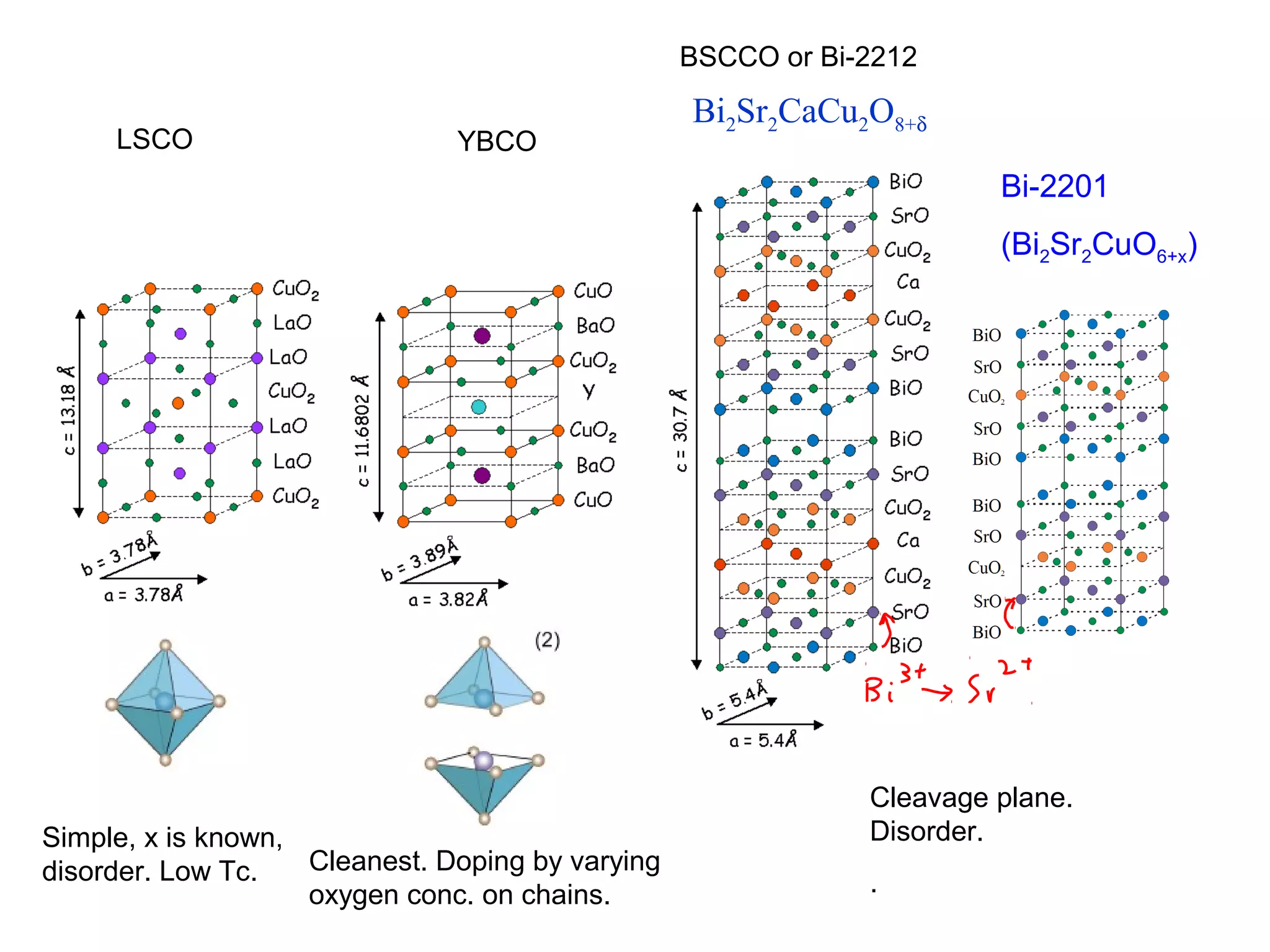
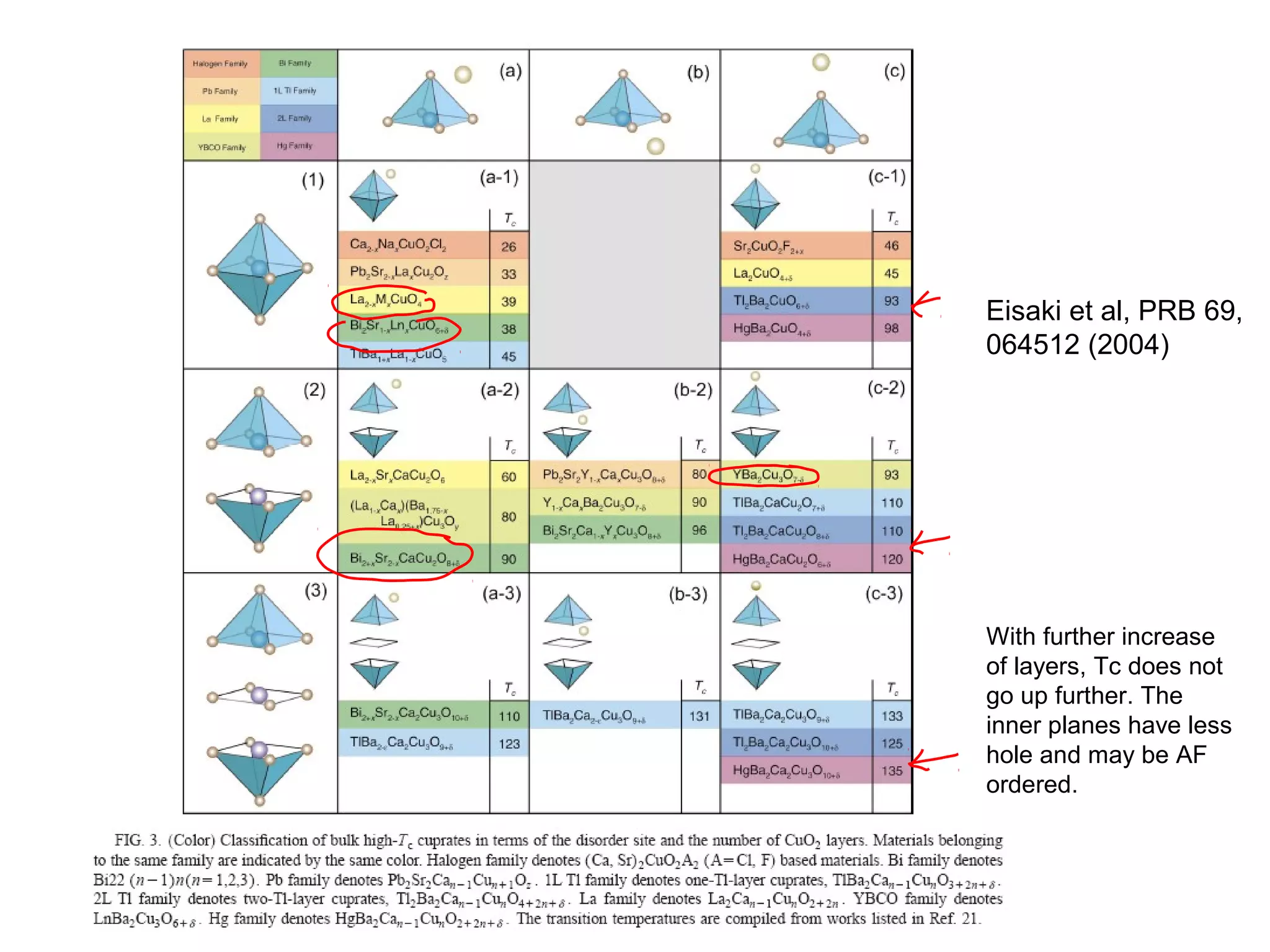
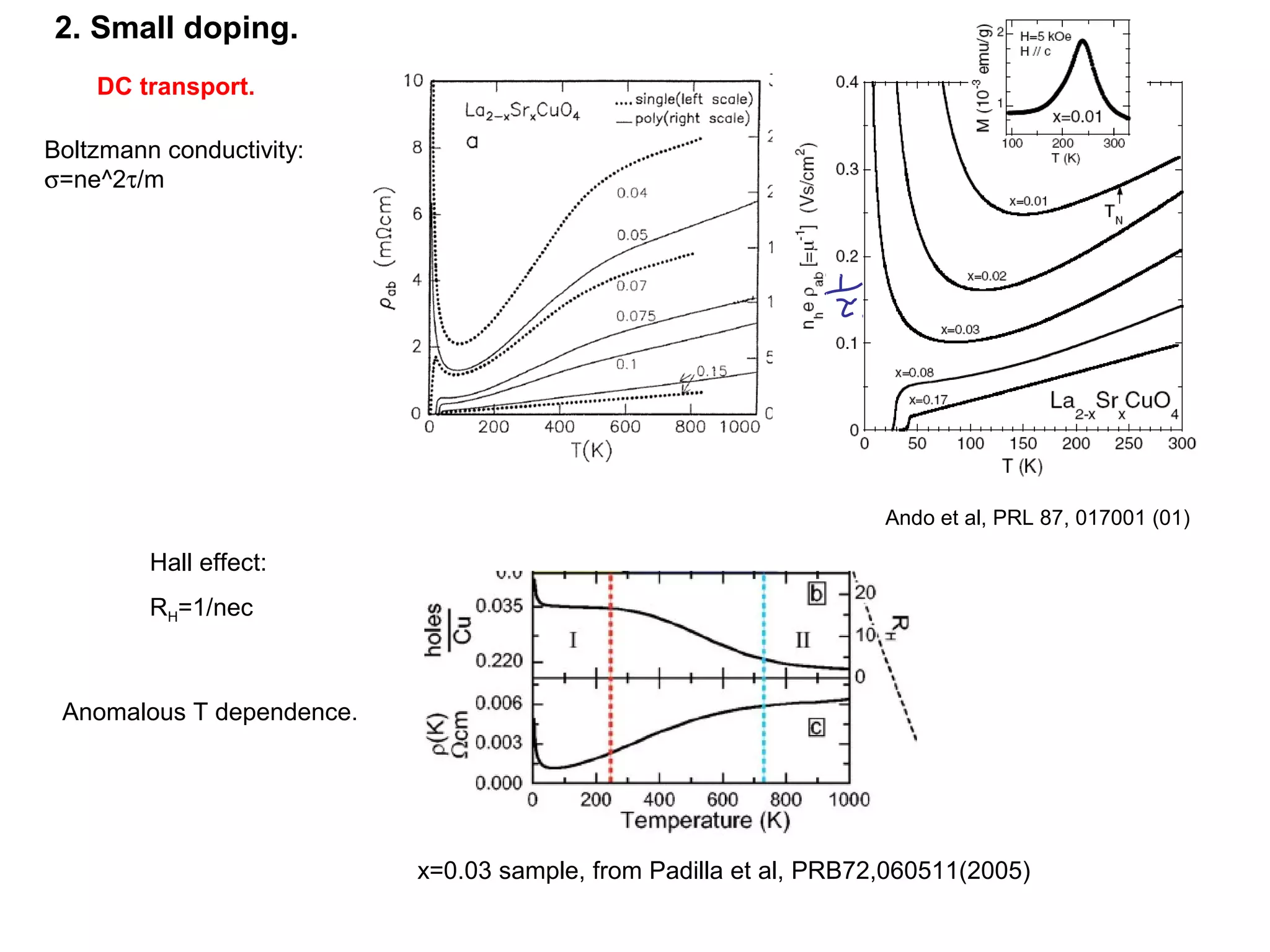
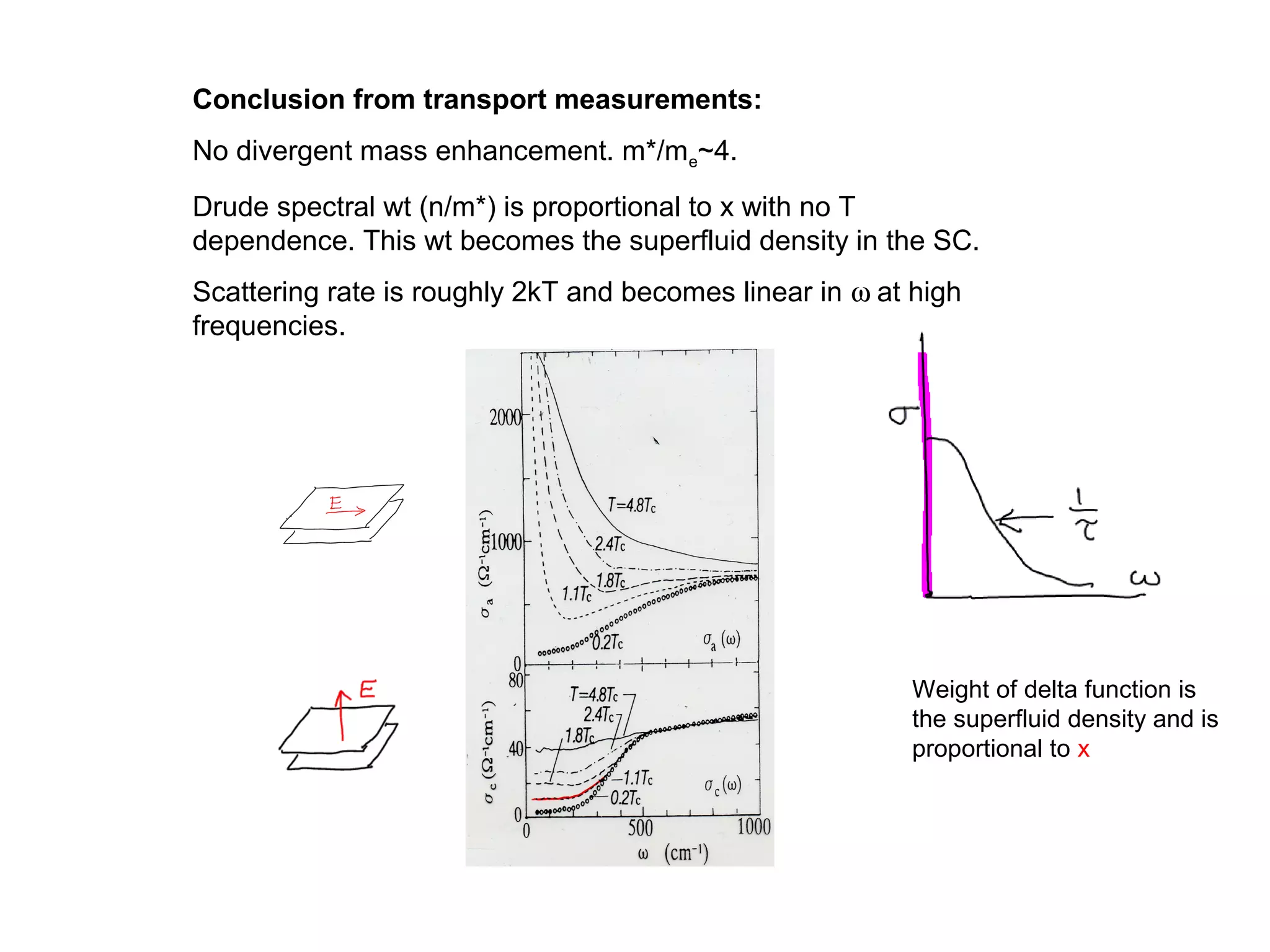
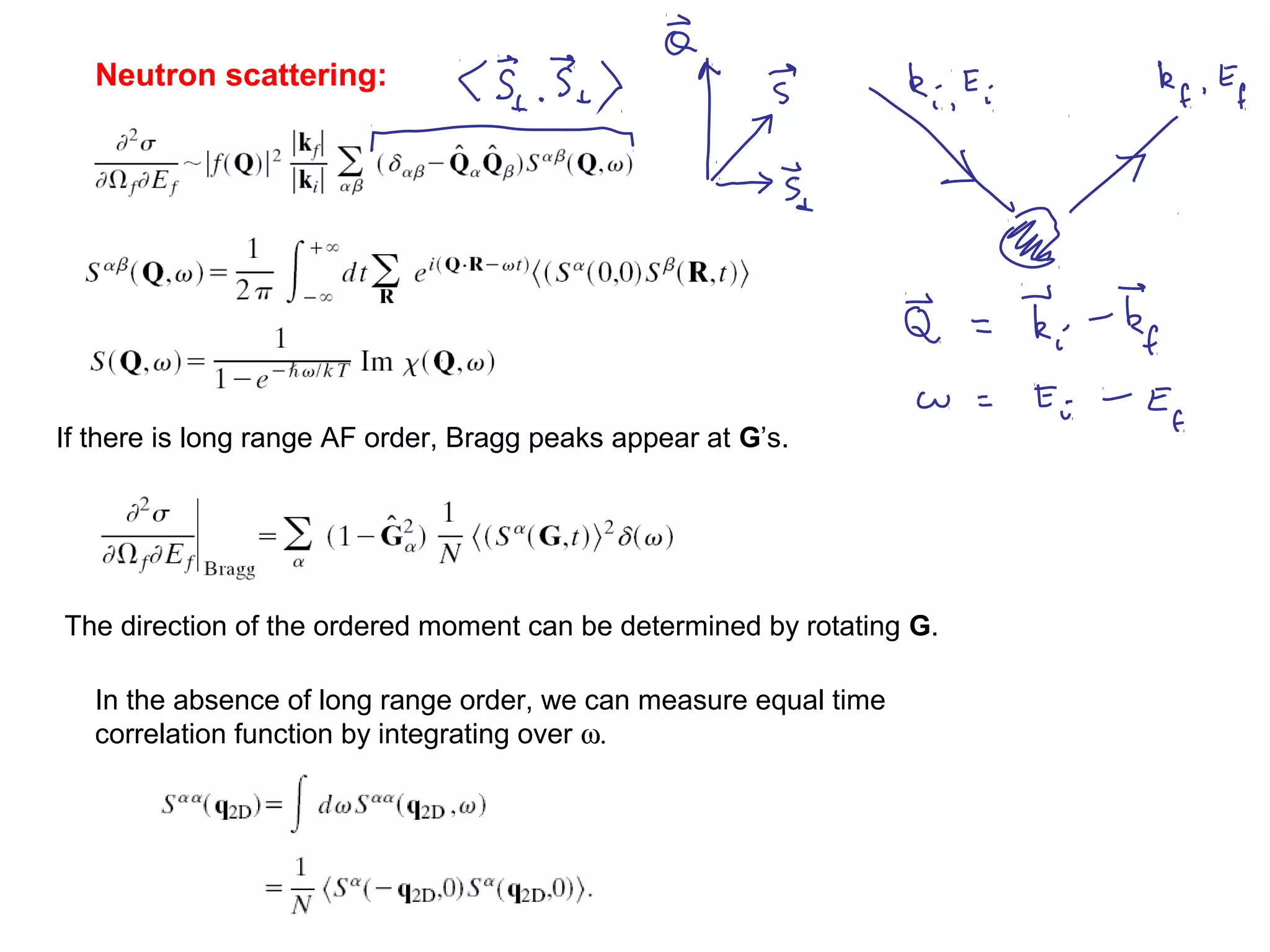
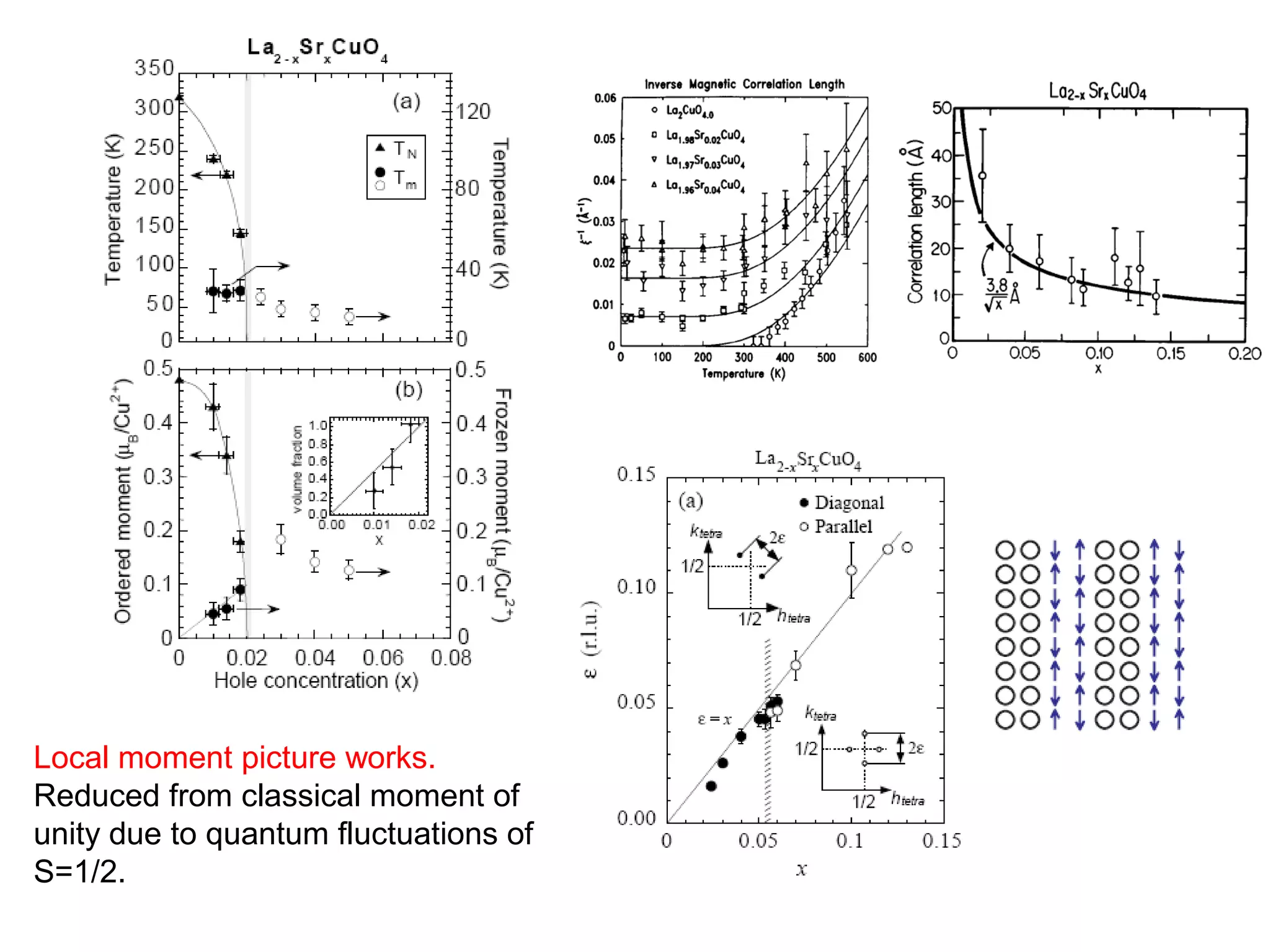
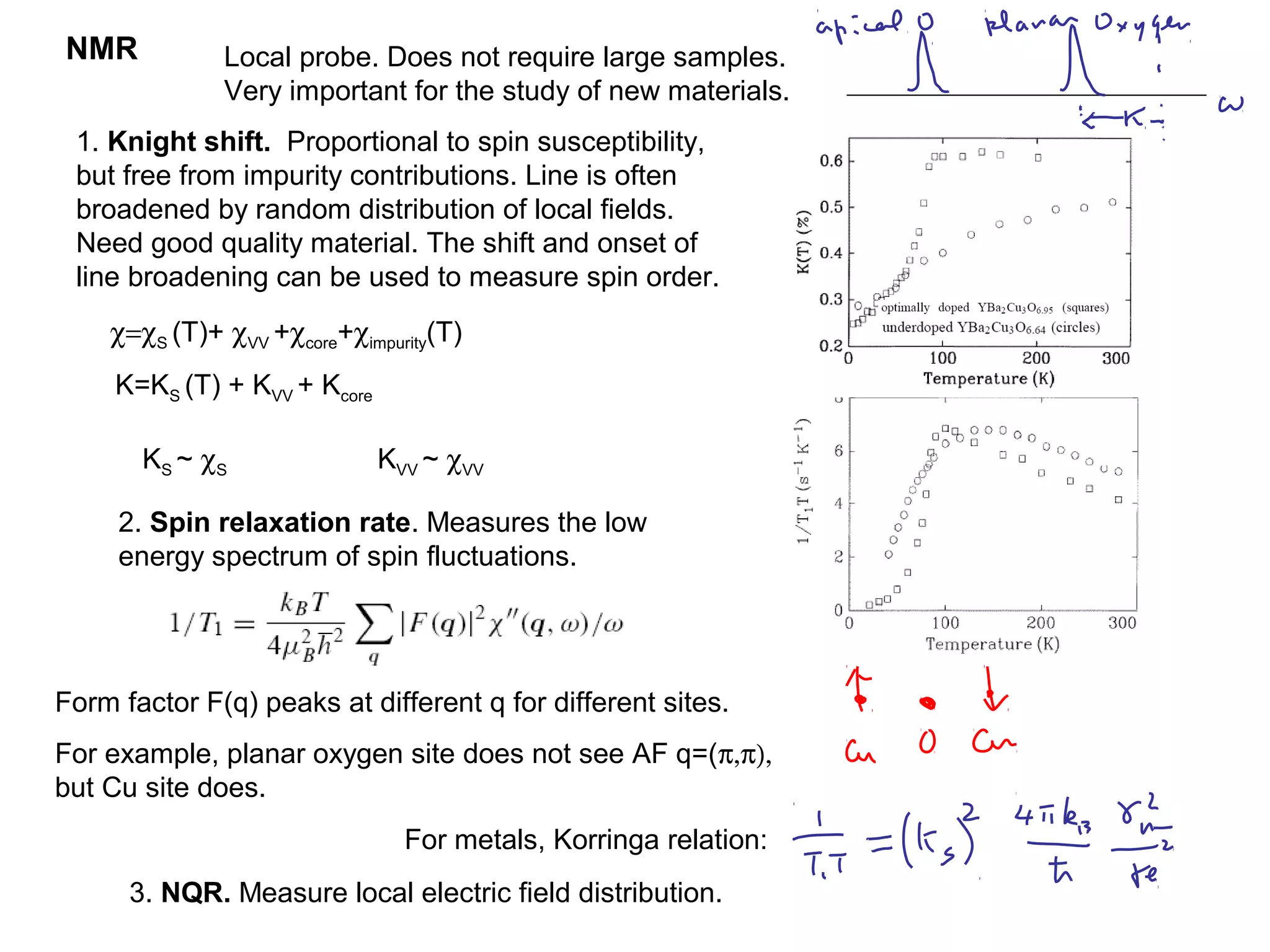
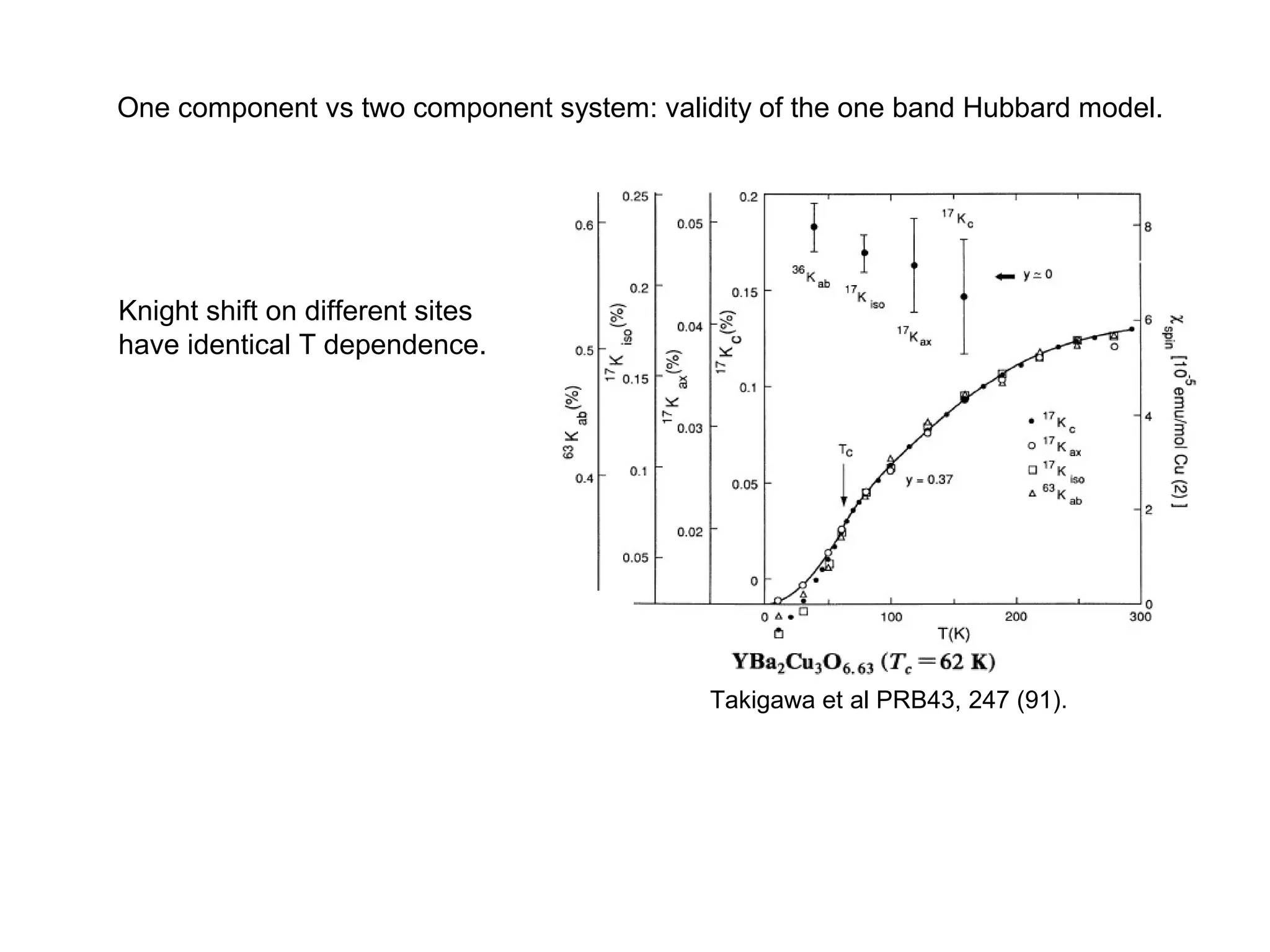
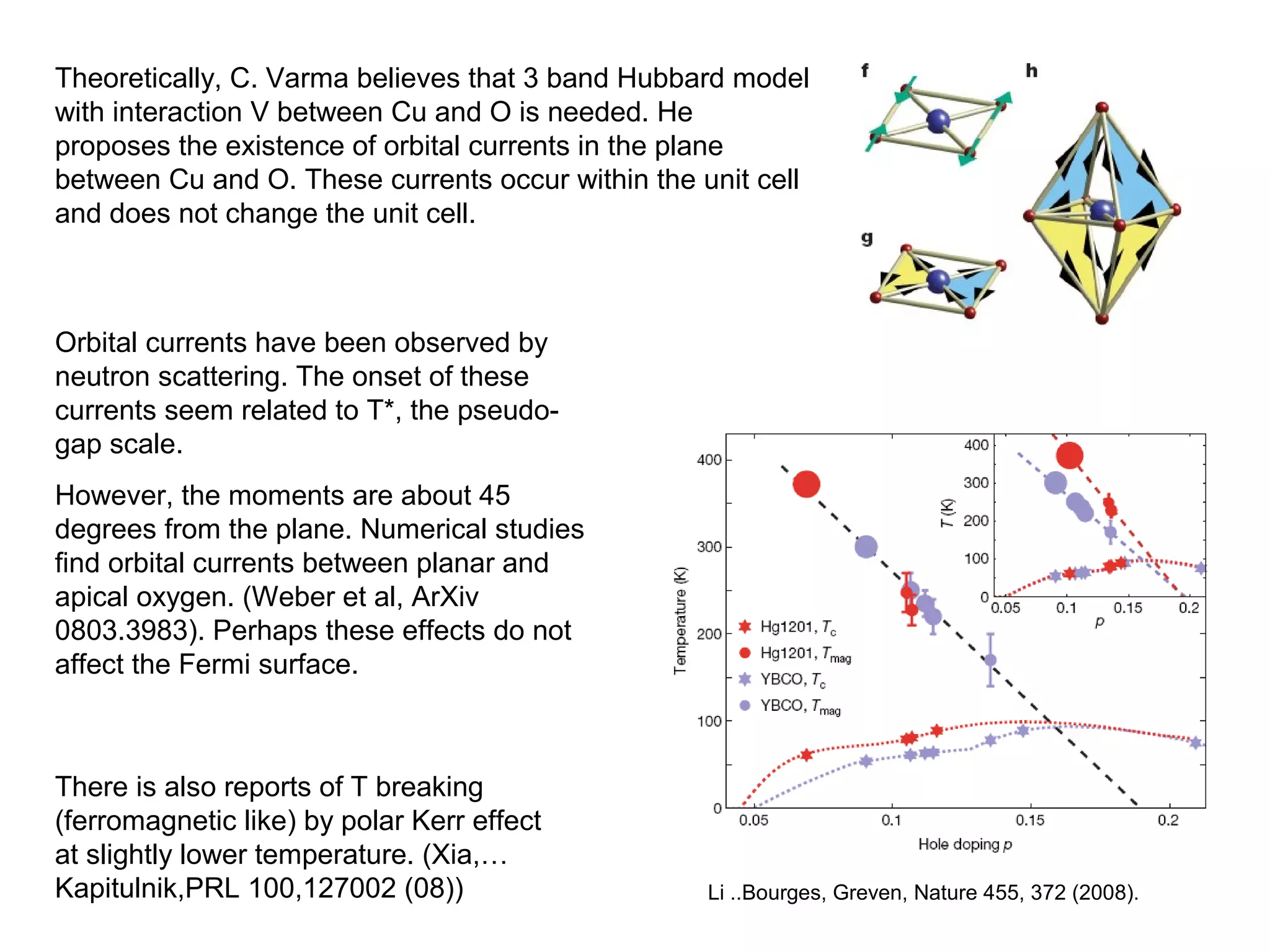
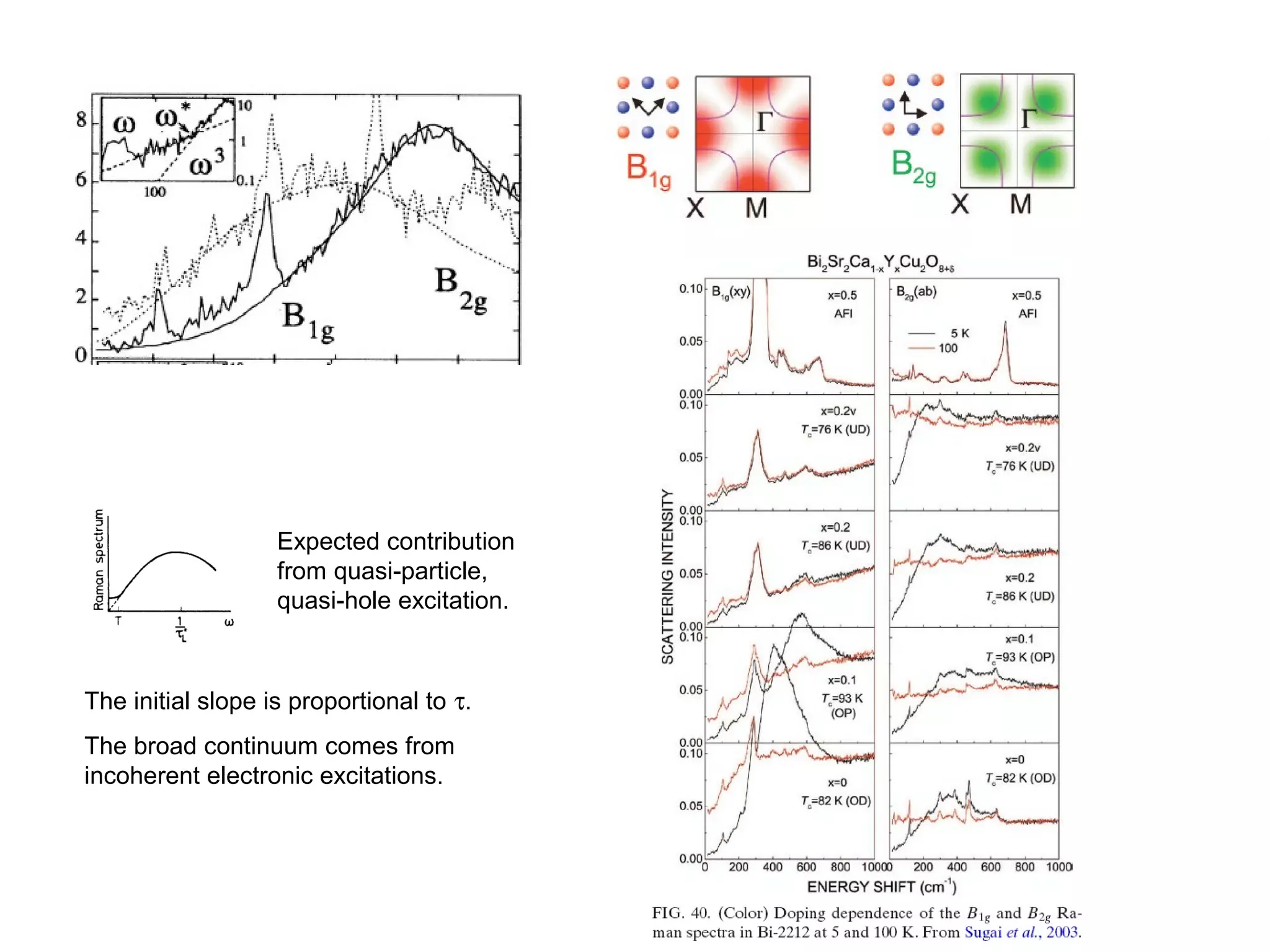
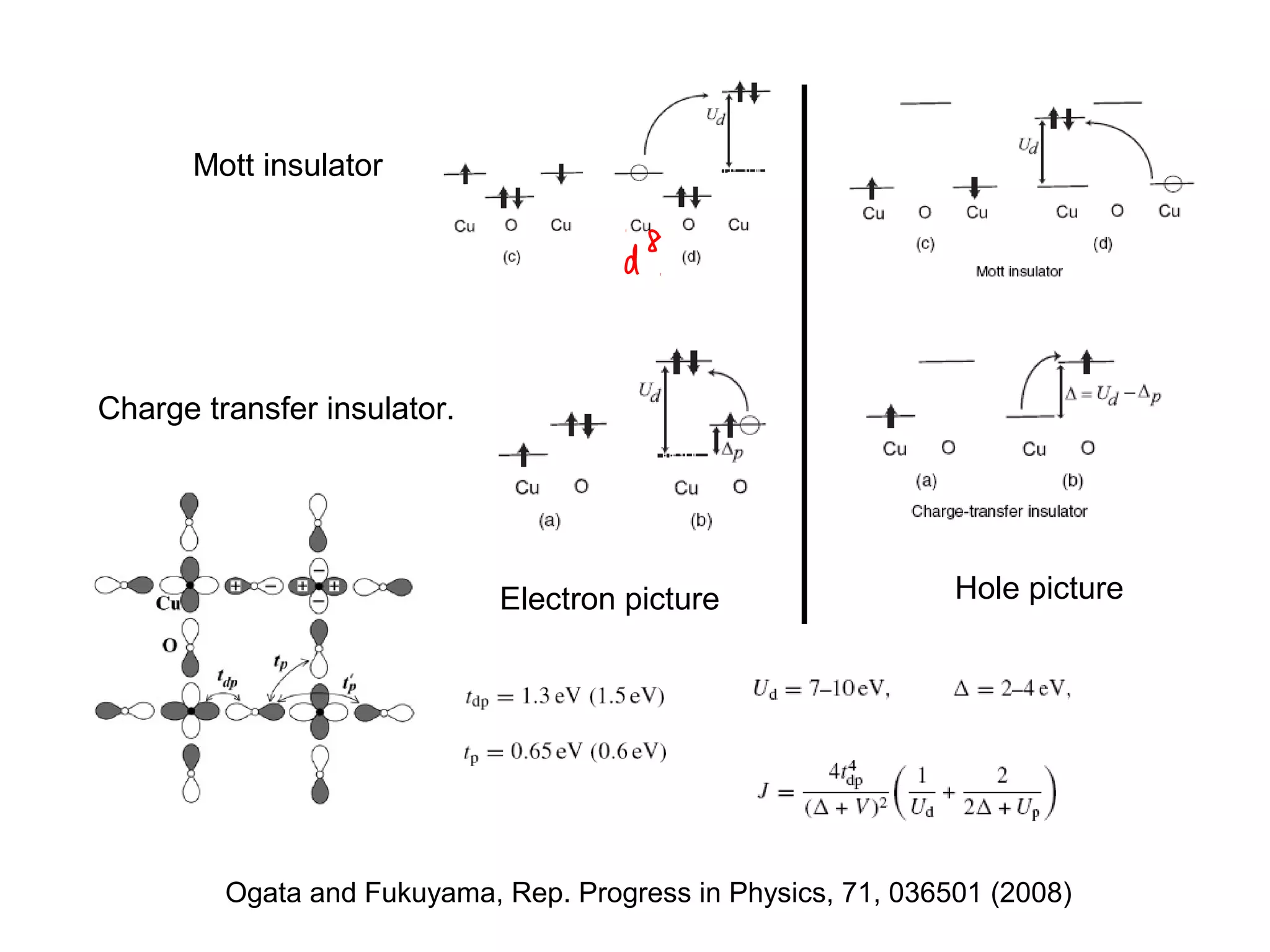
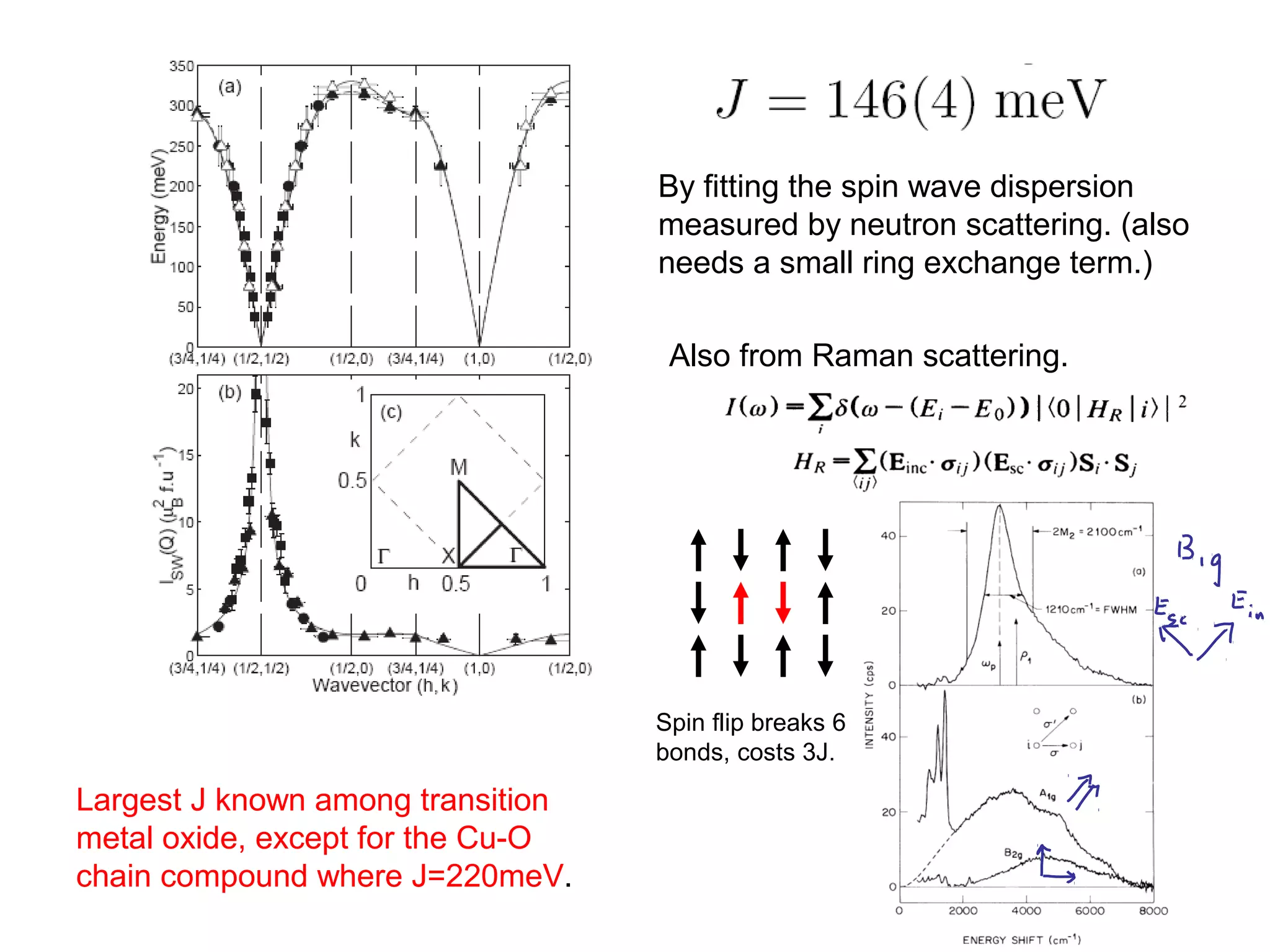
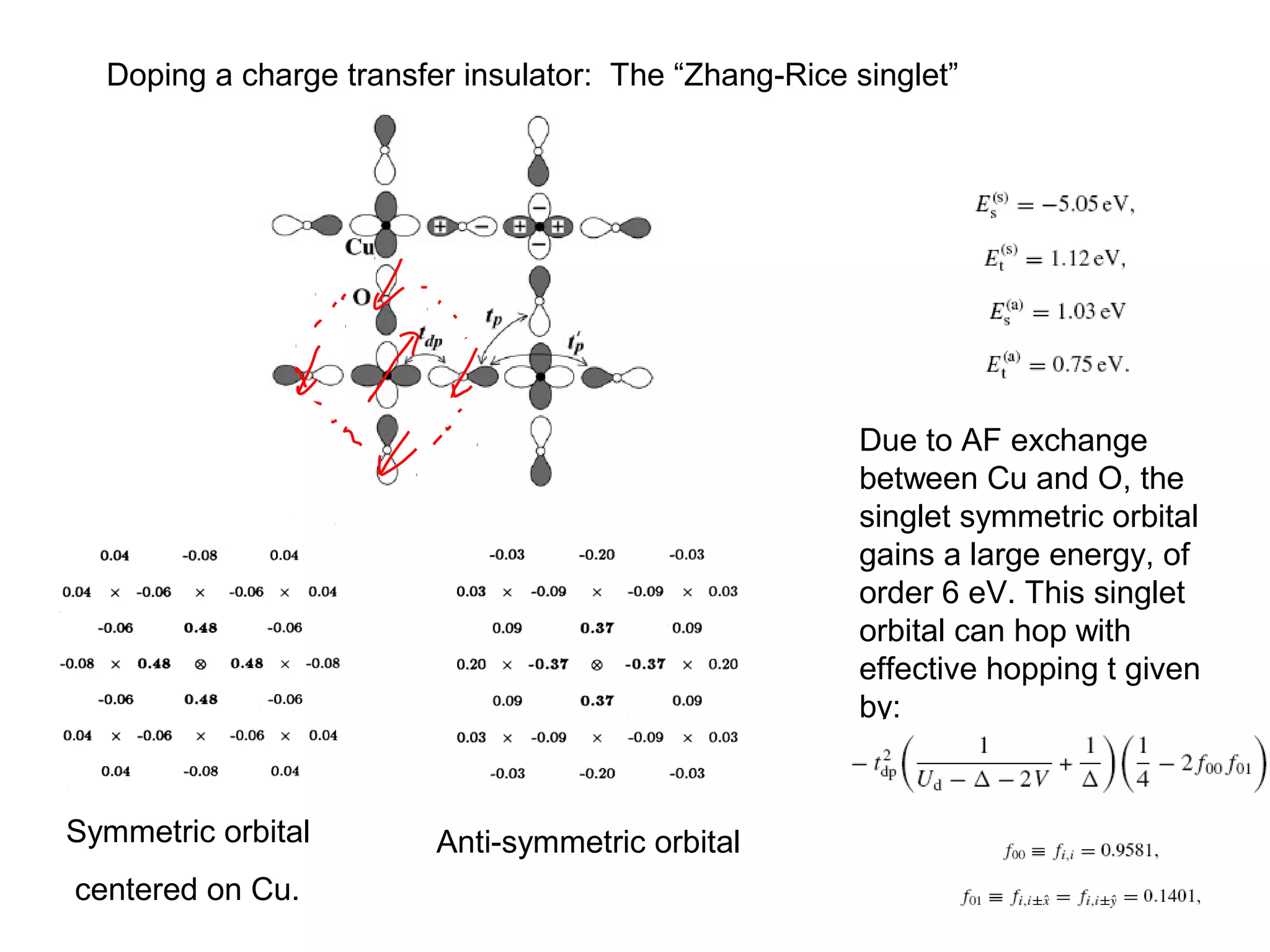
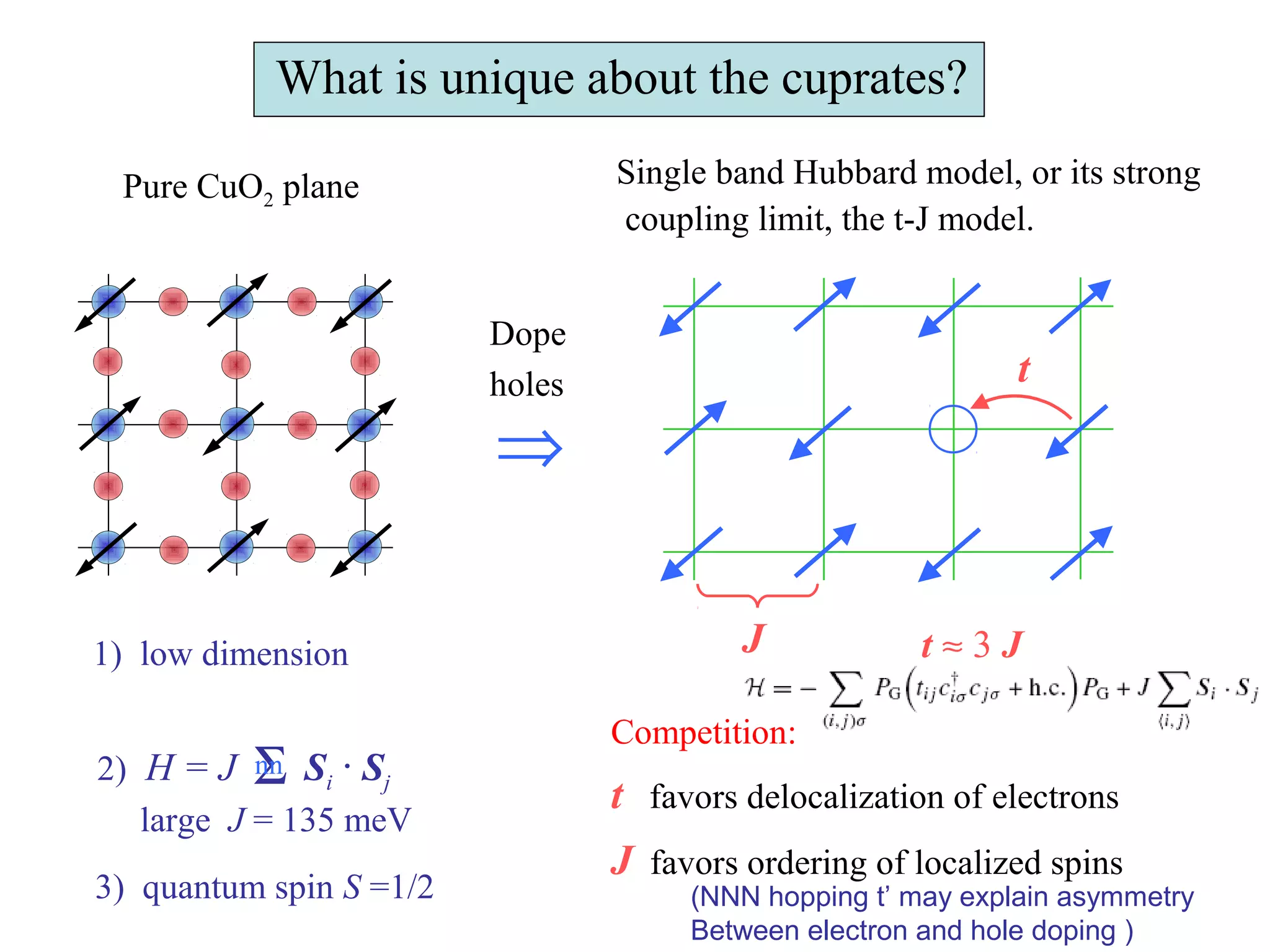
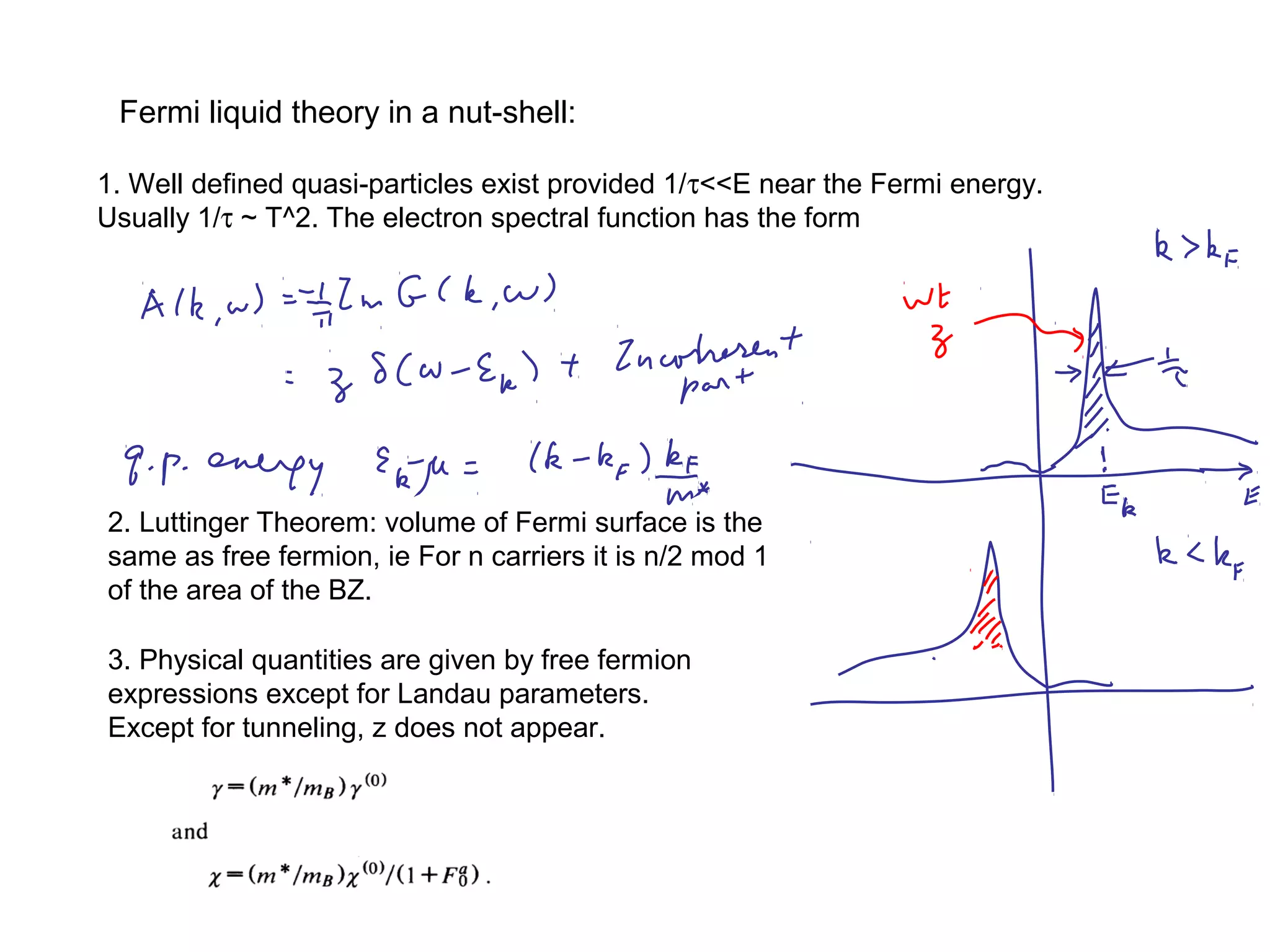
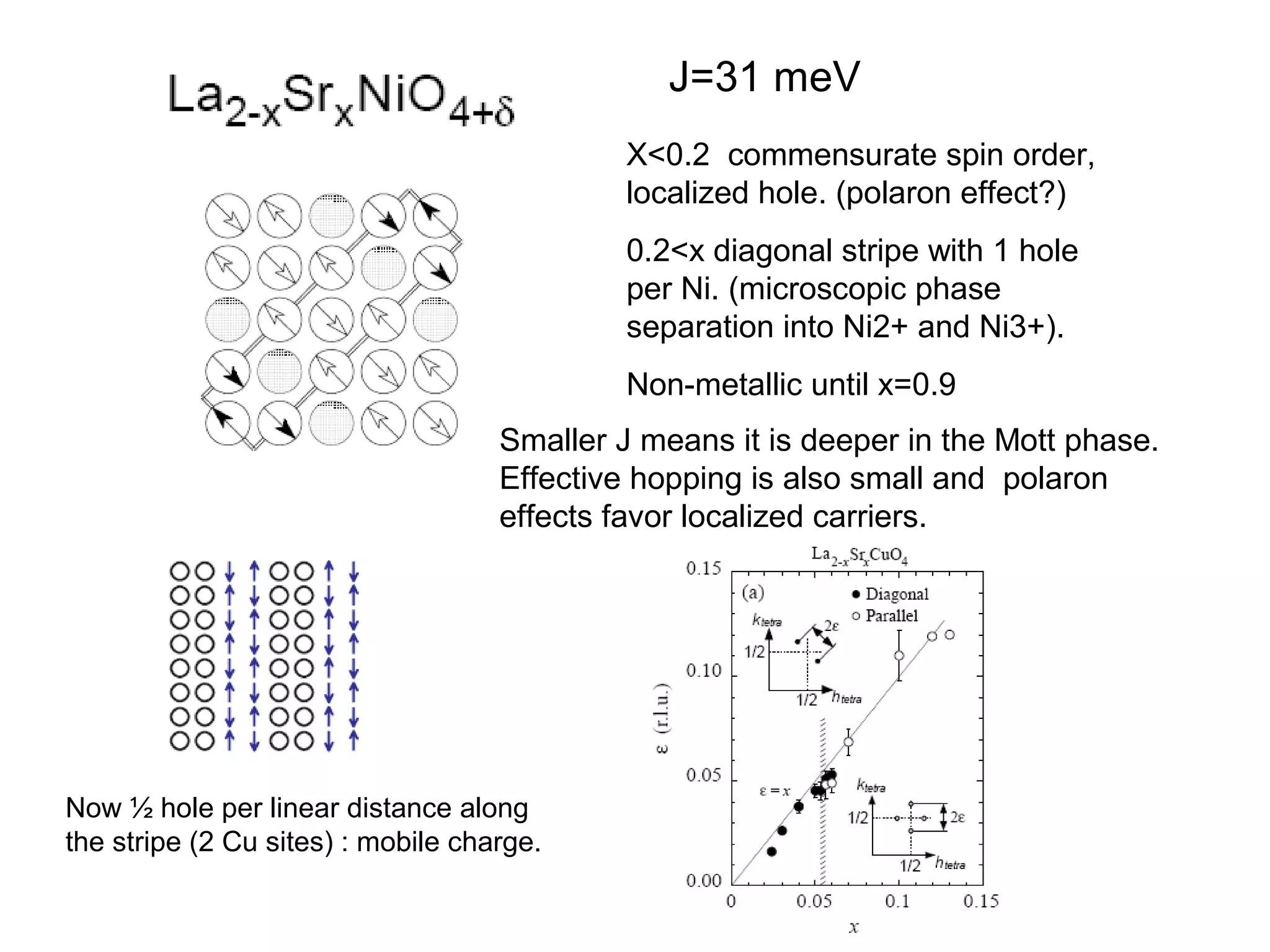
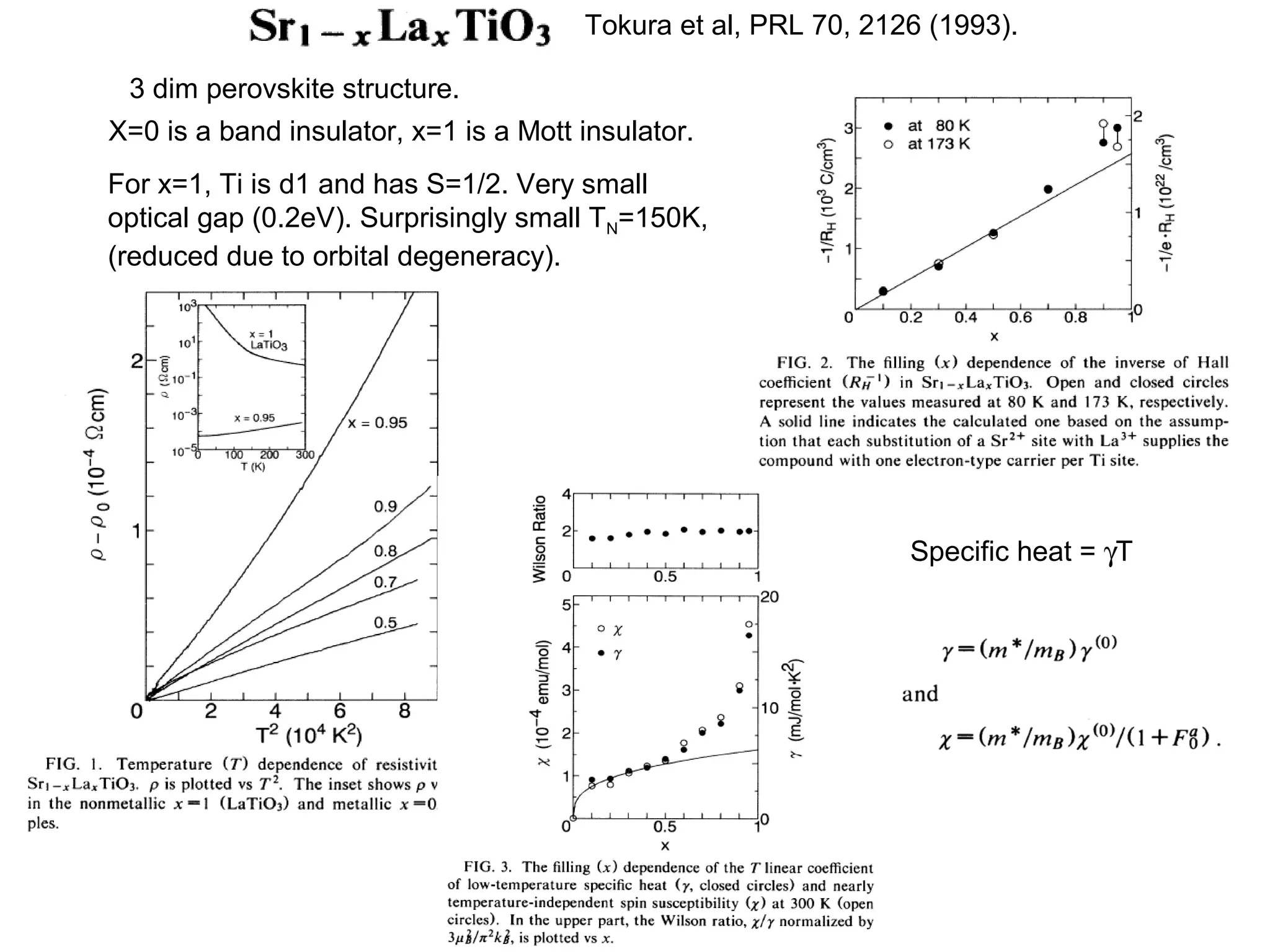
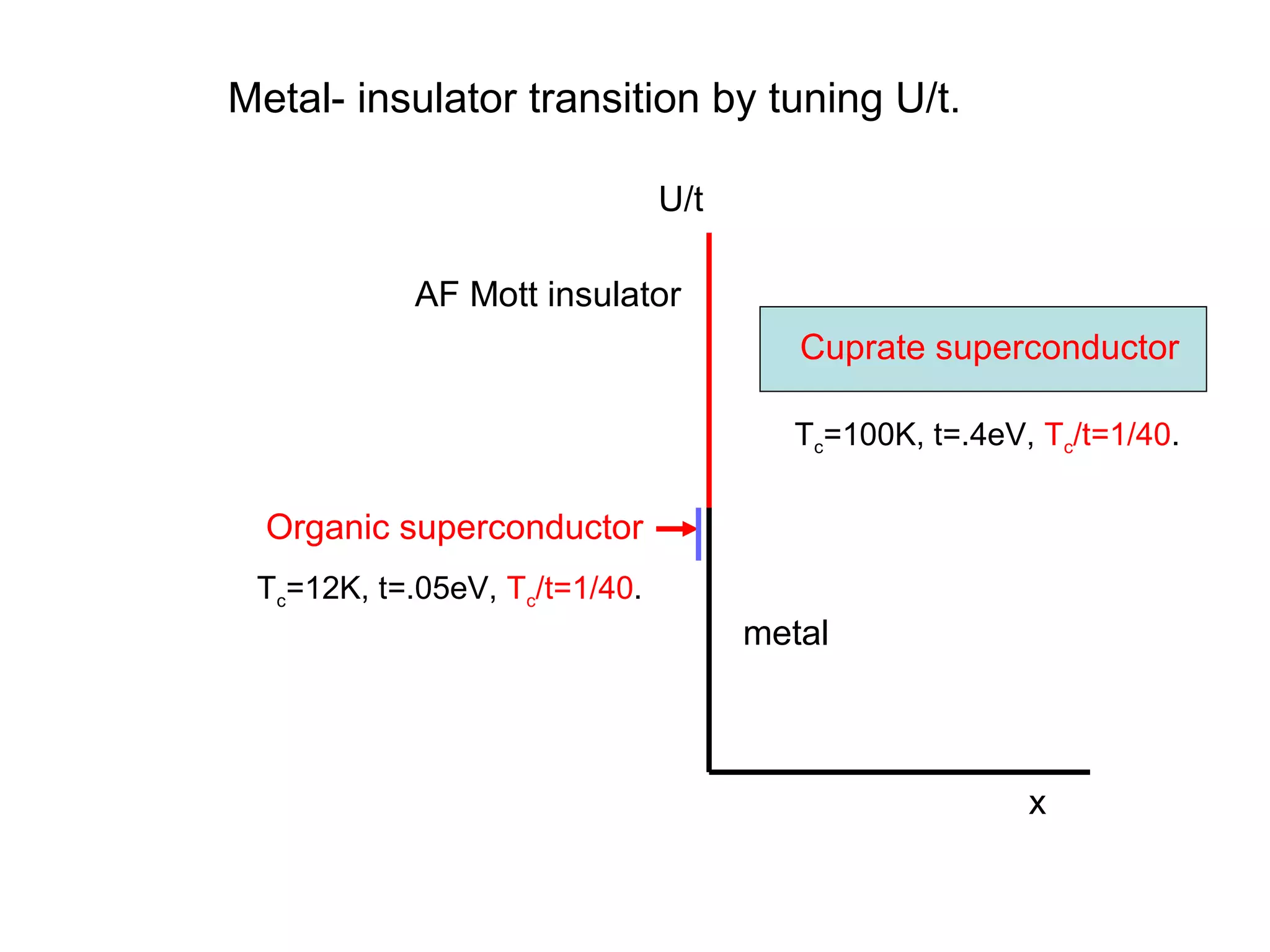
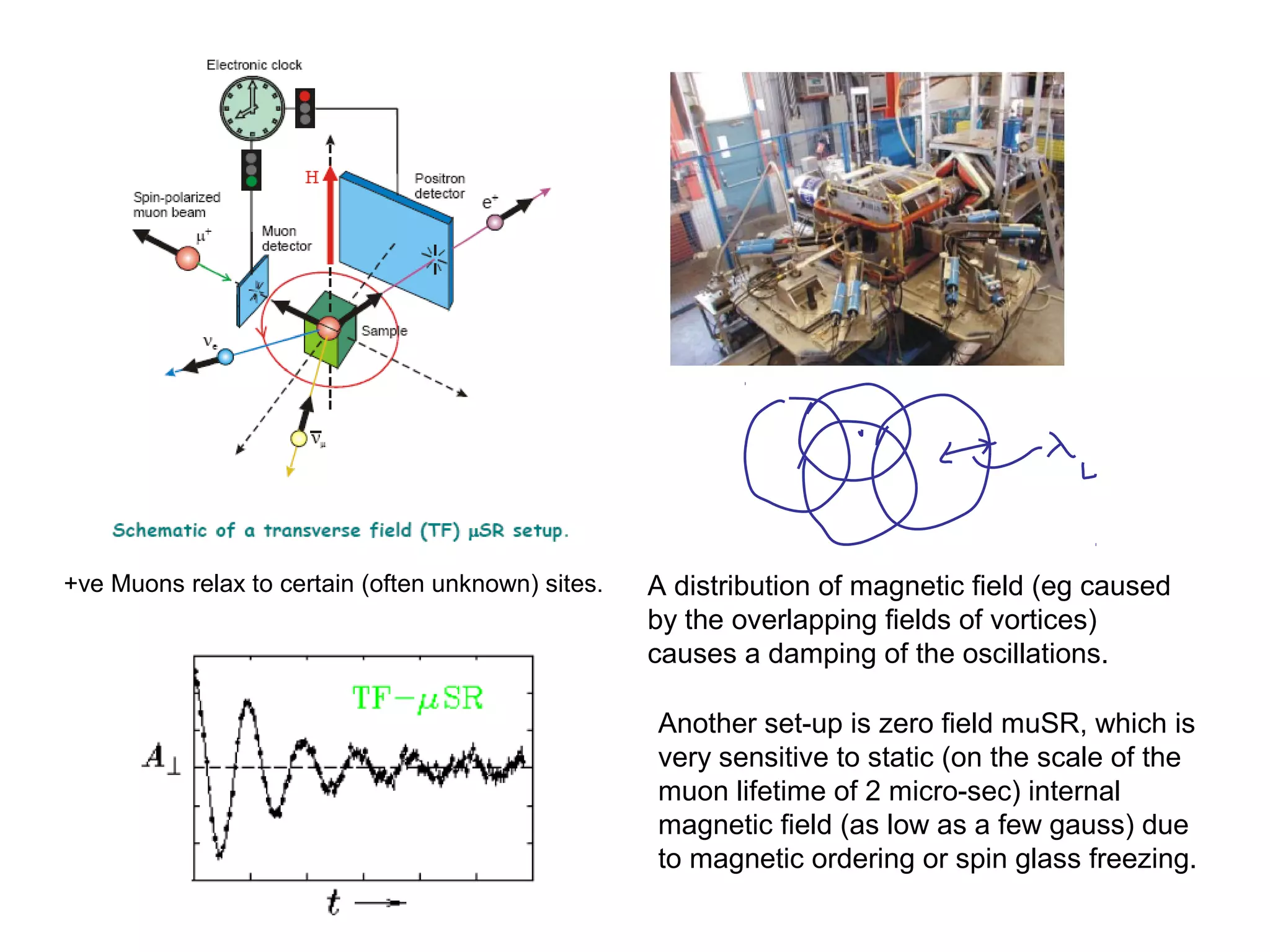
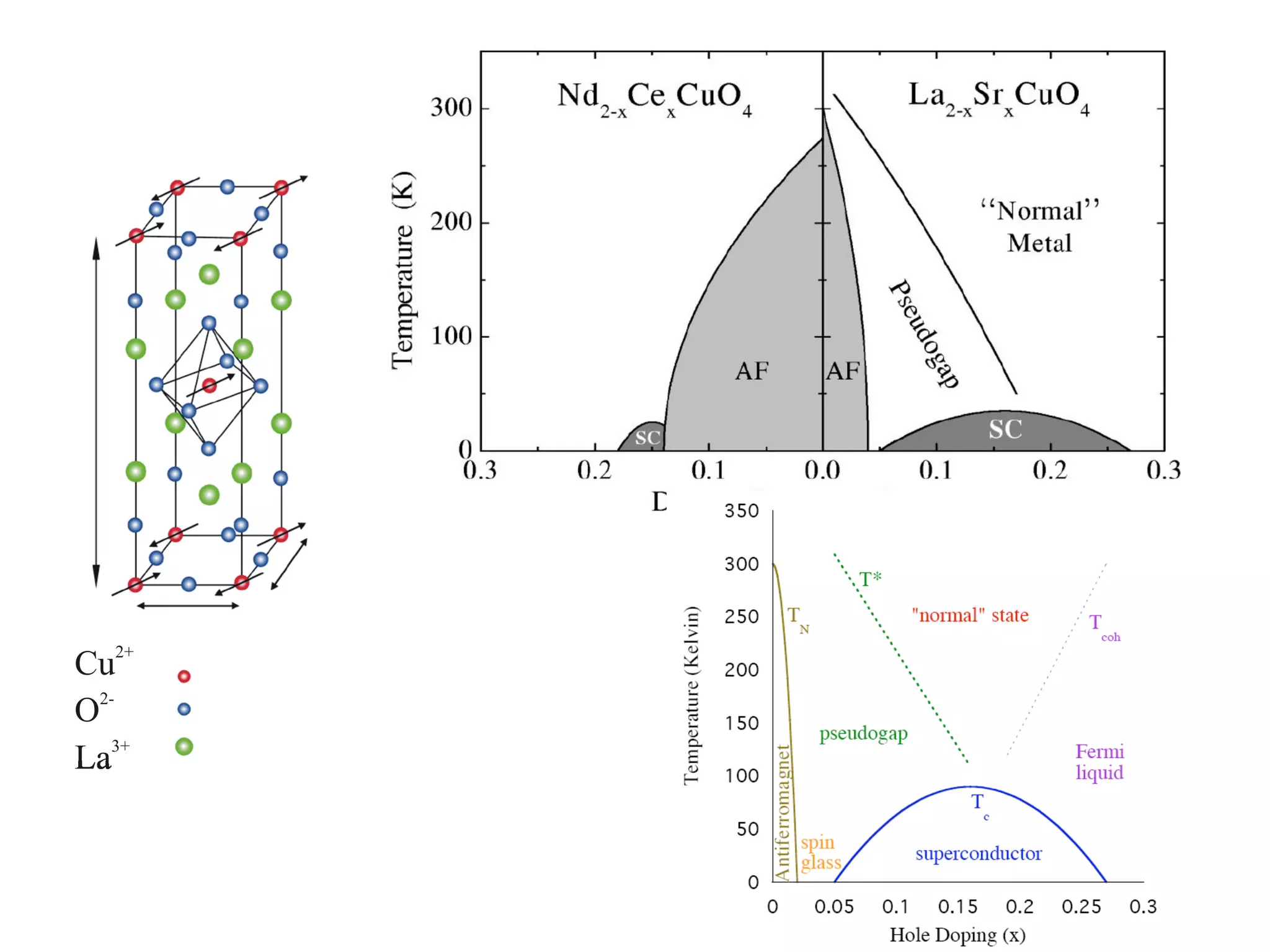
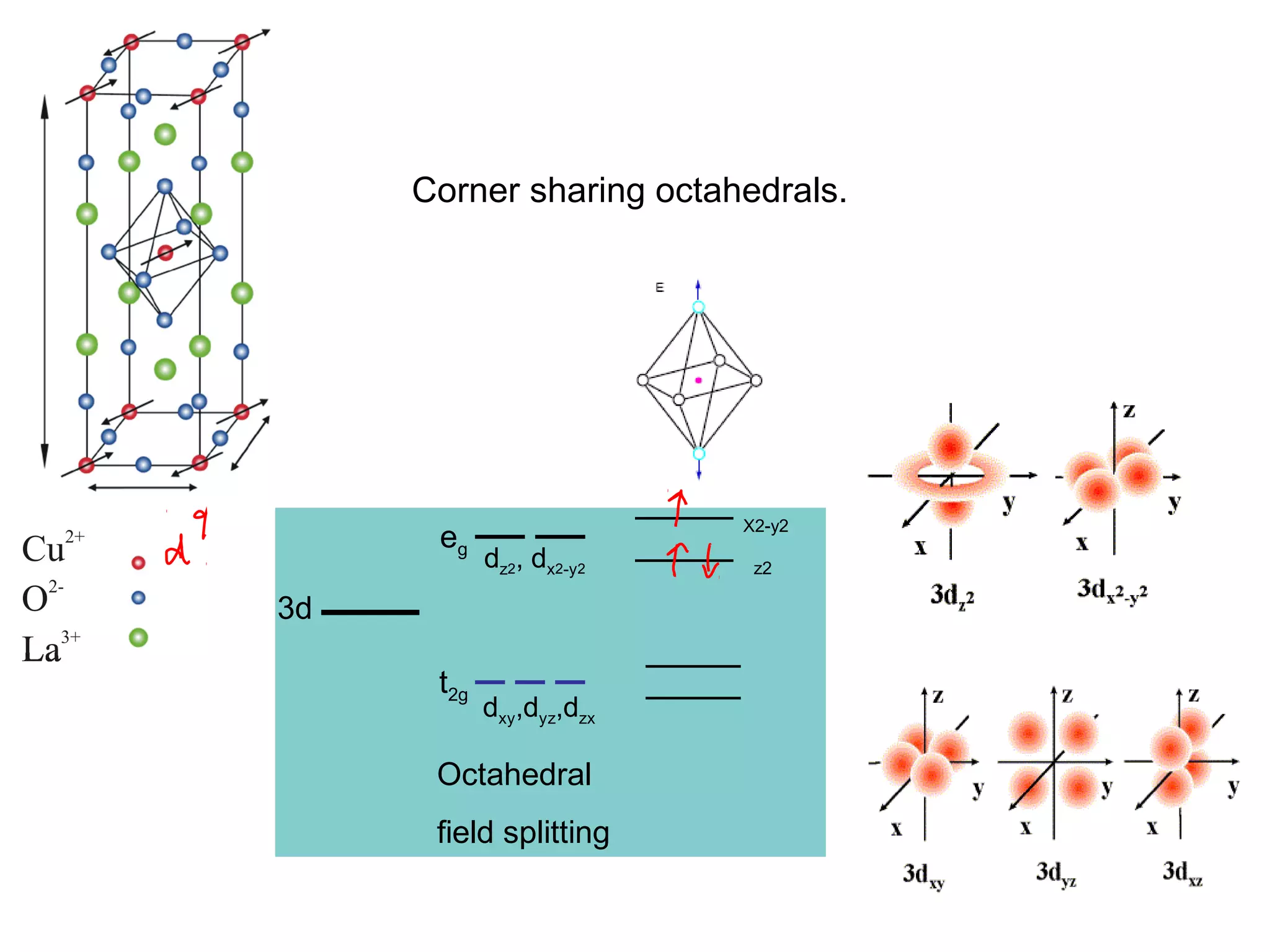
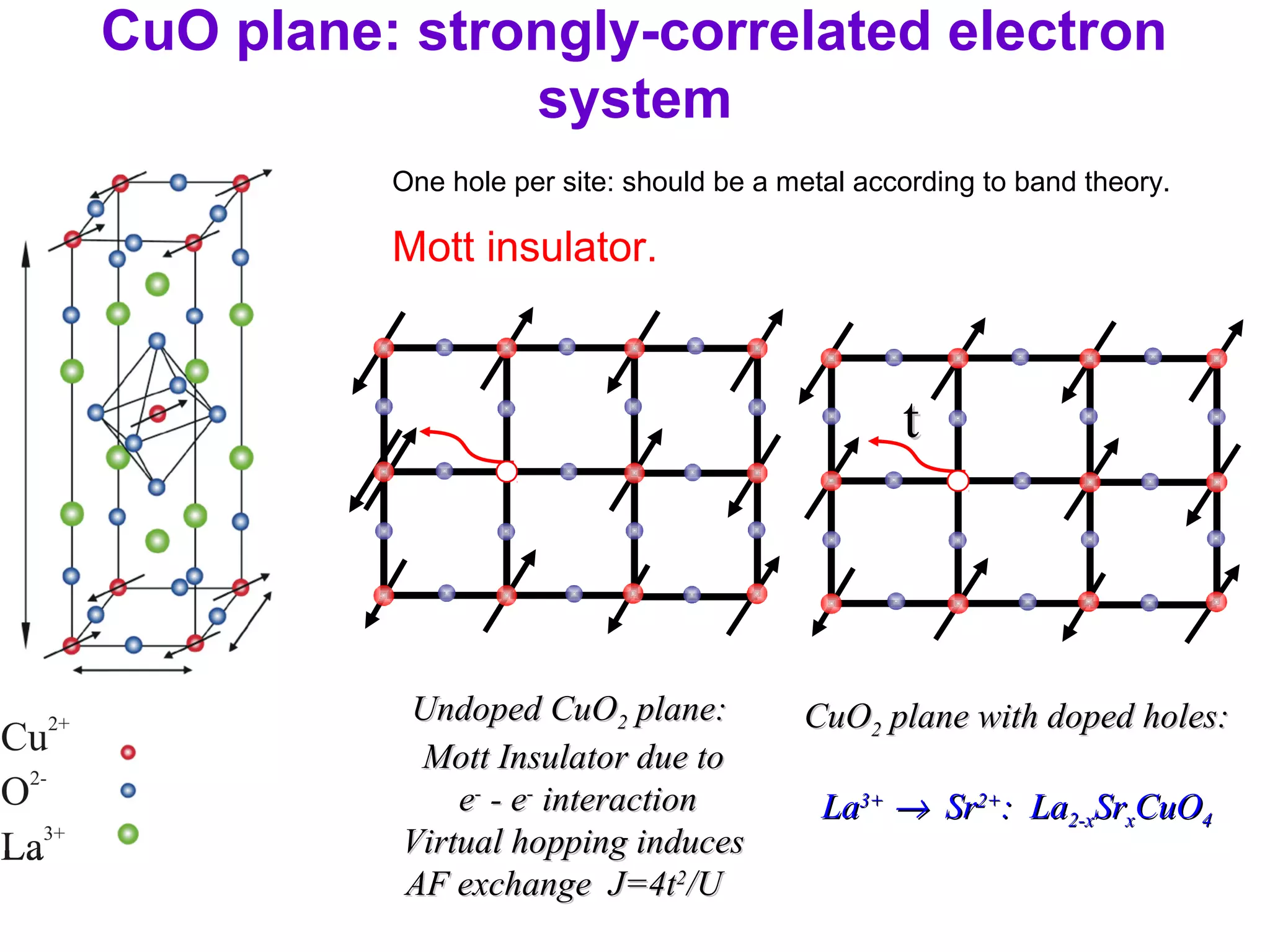
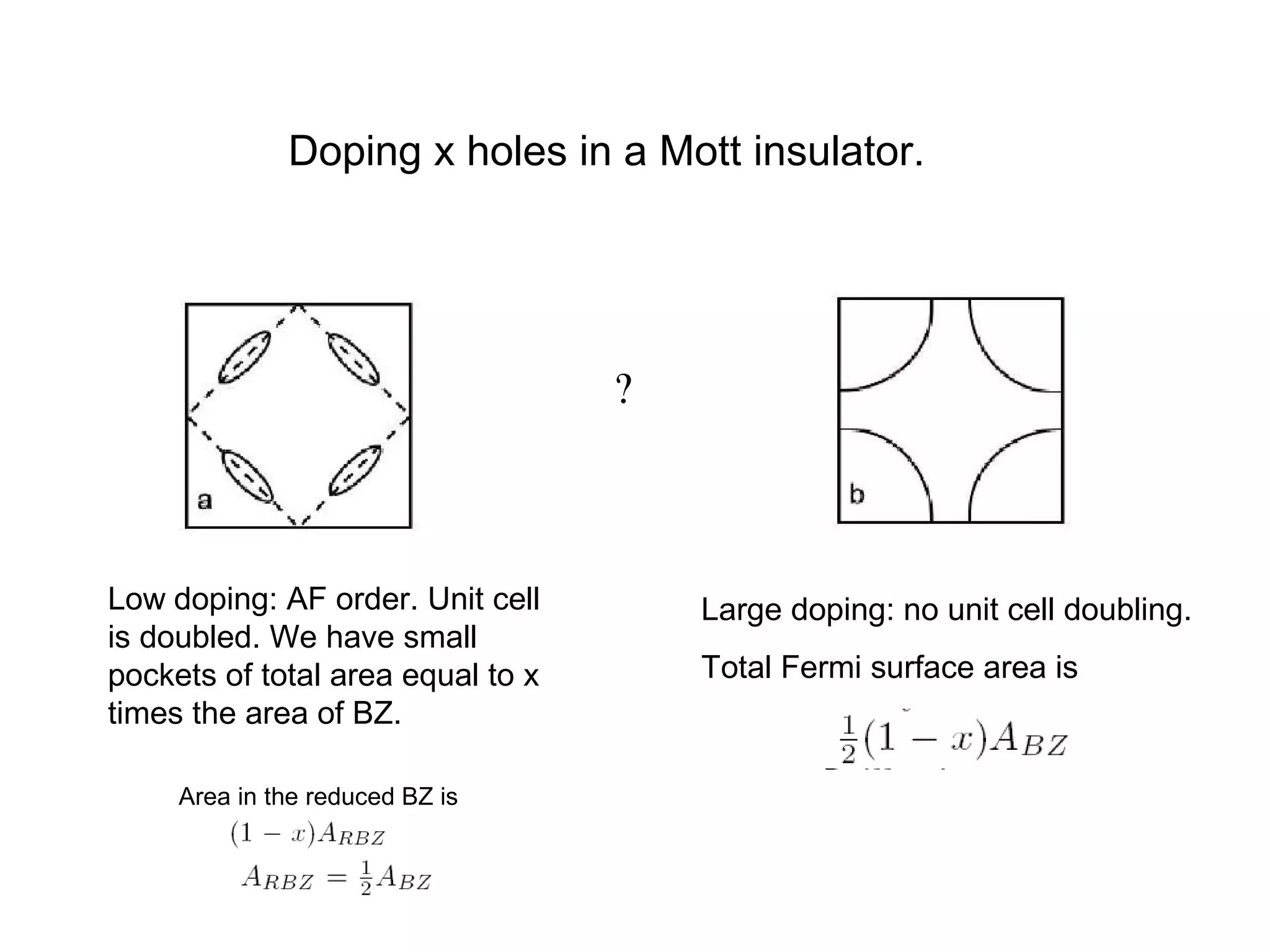
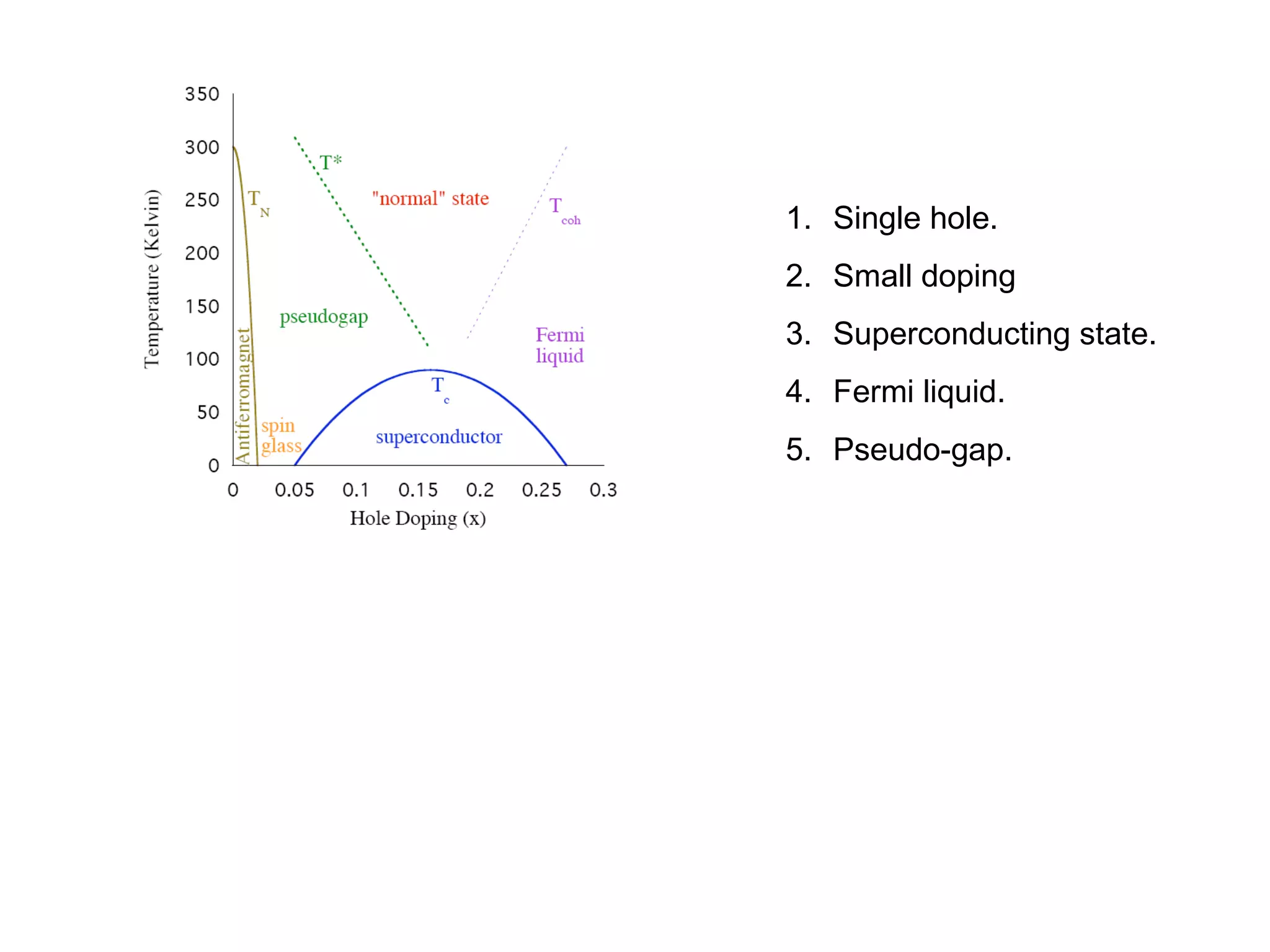
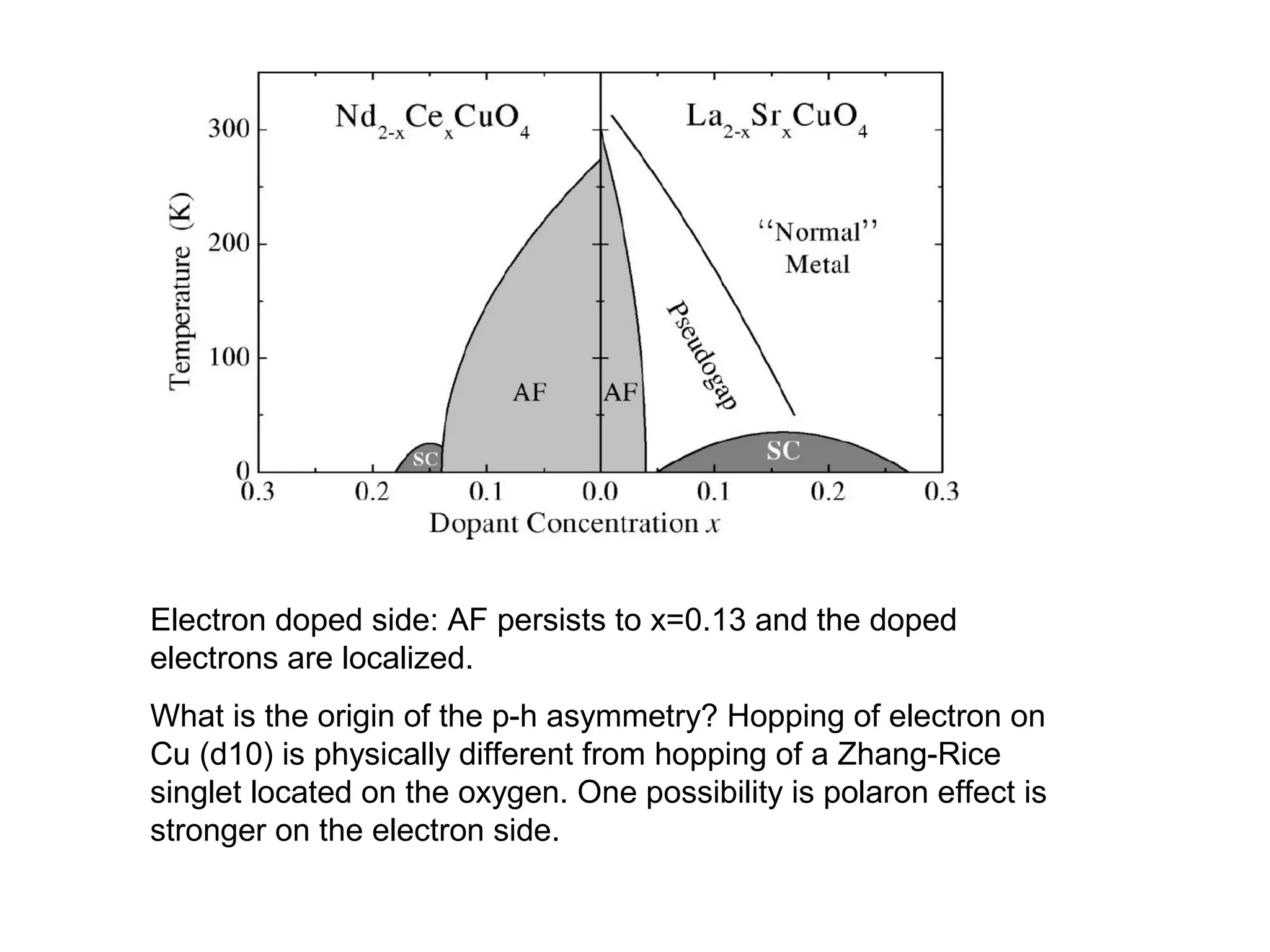
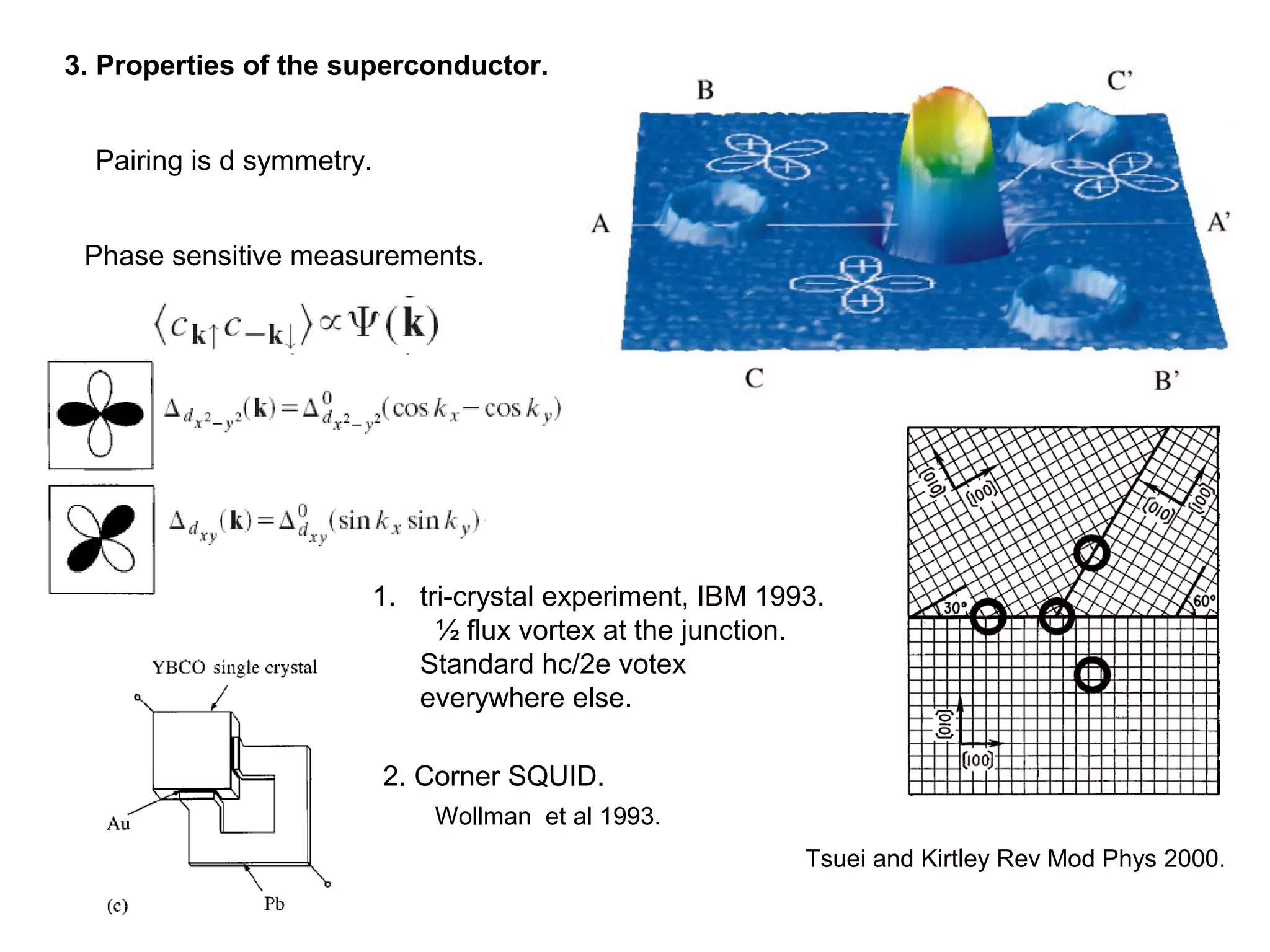
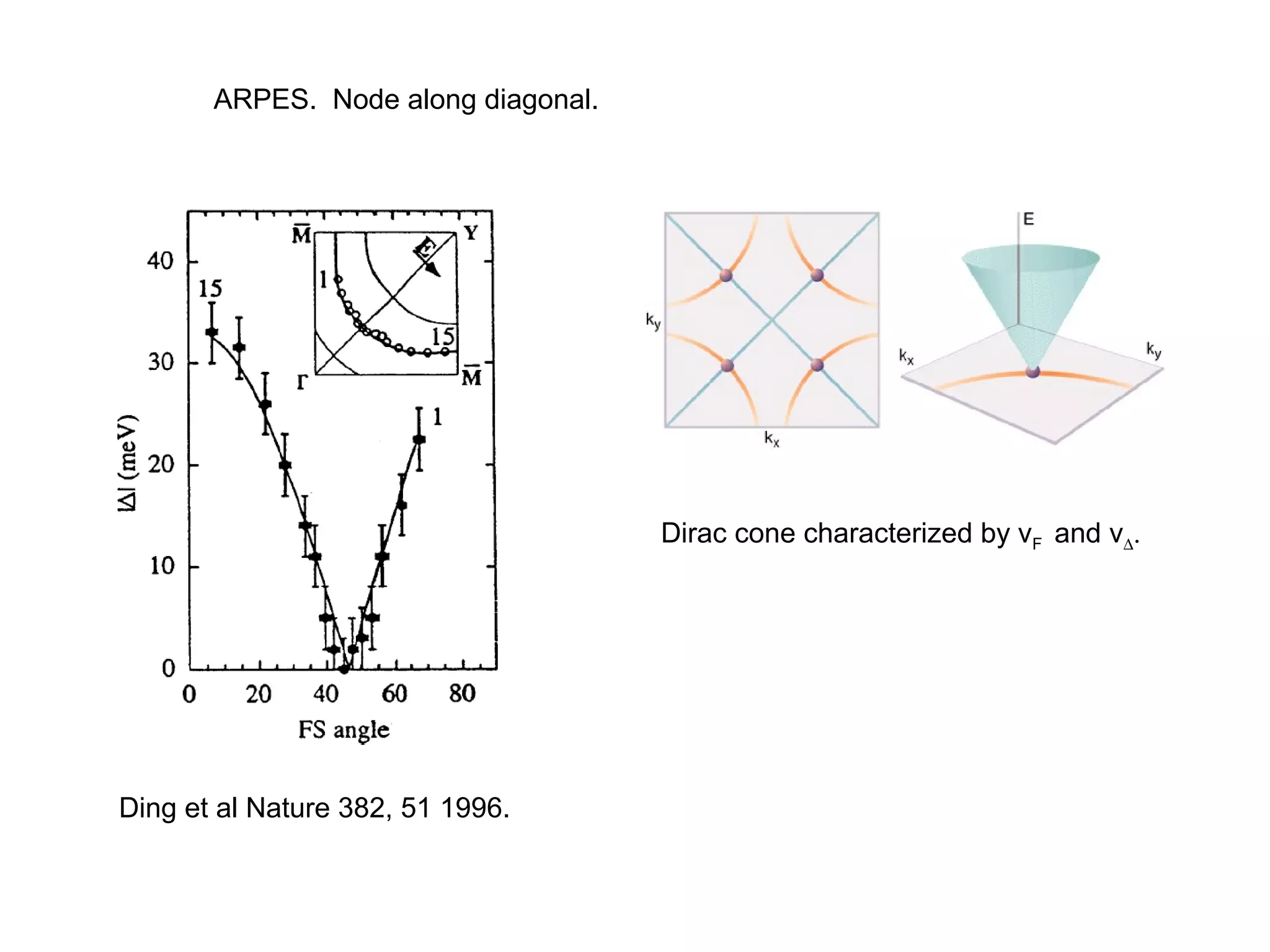
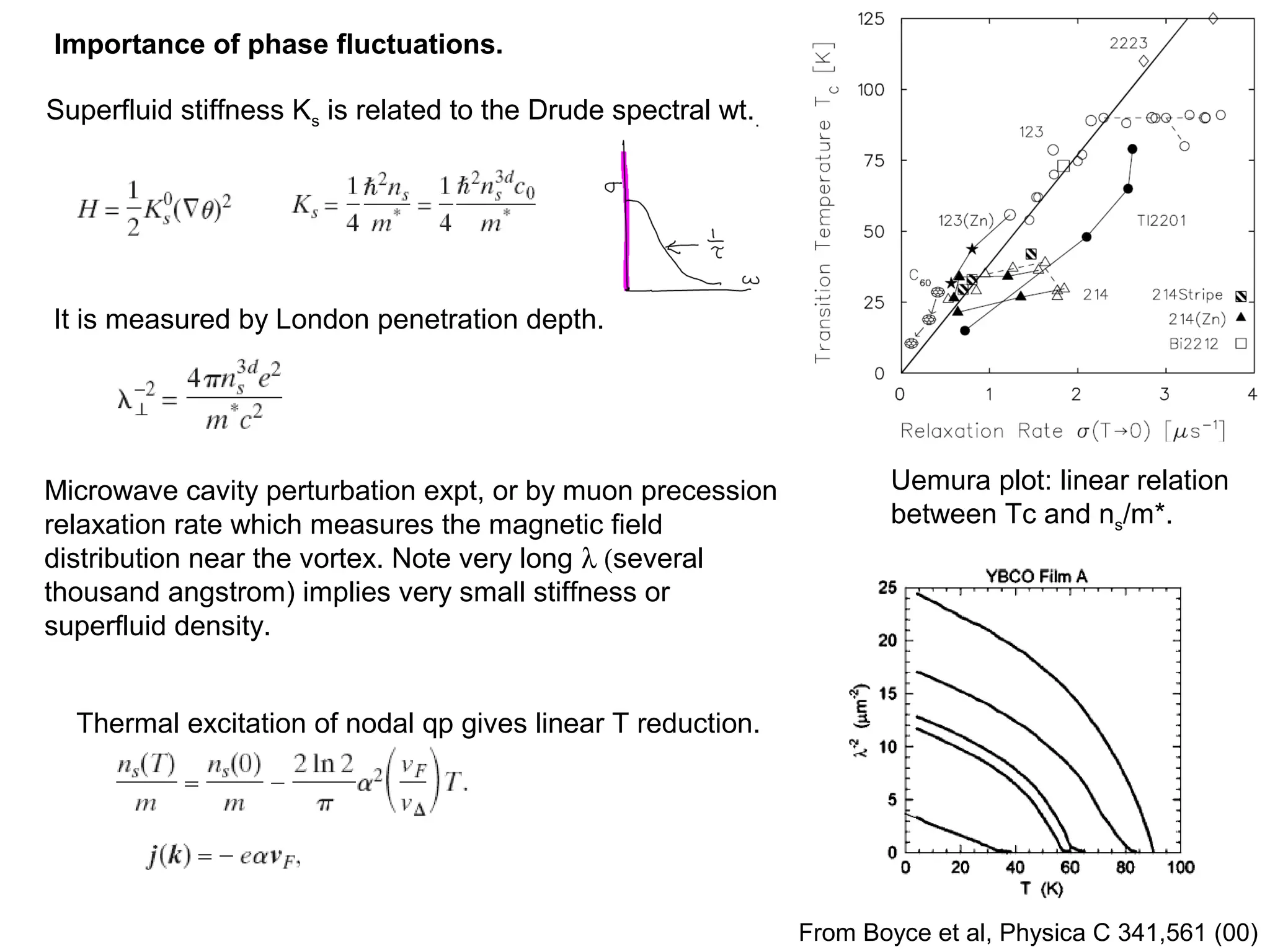
1. The document provides an introduction to the phenomenology of high-temperature superconductors (HiTc). 2. It discusses the basic physics of doped Mott insulators and experimental methods used to study HiTc superconductors such as thermodynamic measurements, transport properties, neutron scattering, and ARPES. 3. It also covers topics such as the pseudo-gap phase, the one-hole problem, properties at small doping levels, and properties of the superconducting state.

1. Introduction to the
phenomenology of HiTc
superconductors.
Patrick Lee and T. Senthil
MIT

2. 1. Basic physics: doped Mott insulator. (Early sections in Lee,
Nagaosa and Wen, Rev Mod Phys,78,17(2006) and Lee, Reports of Progress in
Physics, 71,012501(2008))
2. Introduction to experimental methods.
Thermodynamic measurements: specific heat, spin susceptibility.
Transport: resistivity, Hall, magneto-resistance (angle dependence ADMR).
thermo-power, thermal conductivity.
quantum oscillations.
AC conductivity, optical, microwave and IR, time domain spectroscopy.
Neutron scattering
NMR
ARPES
Tunneling and STM.
3. Pseudo-gap physics.

4. Corner sharing octahedrals.
3d
eg
t2g
dxy,dyz,dzx
dz2, dx2-y2
Octahedral
field splitting
X2-y2
z2

5. CuO plane: strongly-correlated electron
system
Undoped CuOUndoped CuO22 plane:plane:
Mott Insulator due toMott Insulator due to
ee--
- e- e--
interactioninteraction
Virtual hopping inducesVirtual hopping induces
AF exchange J=4tAF exchange J=4t22
/U/U
CuOCuO22 plane with doped holes:plane with doped holes:
LaLa3+3+
→→ SrSr2+2+
: La: La2-x2-xSrSrxxCuOCuO44
tt
One hole per site: should be a metal according to band theory.
Mott insulator.

6. Ogata and Fukuyama, Rep. Progress in Physics, 71, 036501 (2008)
Charge transfer insulator.
Electron picture Hole picture
Mott insulator

7. Also from Raman scattering.
Largest J known among transition
metal oxide, except for the Cu-O
chain compound where J=220meV.
By fitting the spin wave dispersion
measured by neutron scattering. (also
needs a small ring exchange term.)
Spin flip breaks 6
bonds, costs 3J.

8. Doping a charge transfer insulator: The “Zhang-Rice singlet”
Symmetric orbital
centered on Cu.
Anti-symmetric orbital
Due to AF exchange
between Cu and O, the
singlet symmetric orbital
gains a large energy, of
order 6 eV. This singlet
orbital can hop with
effective hopping t given
by:

9. What is unique about the cuprates?
Pure CuO2 plane Single band Hubbard model, or its strong
coupling limit, the t-J model.
⇒
Dope
holes t
J t ≈ 3 J1) low dimension
2) H = J Σ Si · Sj
nn
large J = 135 meV
Competition:
t favors delocalization of electrons
J favors ordering of localized spins
3) quantum spin S =1/2 (NNN hopping t’ may explain asymmetry
Between electron and hole doping )

10. Fermi liquid theory in a nut-shell:
2. Luttinger Theorem: volume of Fermi surface is the
same as free fermion, ie For n carriers it is n/2 mod 1
of the area of the BZ.
1. Well defined quasi-particles exist provided 1/τ<<E near the Fermi energy.
Usually 1/τ ~ T^2. The electron spectral function has the form
3. Physical quantities are given by free fermion
expressions except for Landau parameters.
Except for tunneling, z does not appear.

11. Low doping: AF order. Unit cell
is doubled. We have small
pockets of total area equal to x
times the area of BZ.
Doping x holes in a Mott insulator.
Large doping: no unit cell doubling.
Total Fermi surface area is
Area in the reduced BZ is
?

12. 1. Single hole.
2. Small doping
3. Superconducting state.
4. Fermi liquid.
5. Pseudo-gap.

13. How many ways does Nature have to deal with doping a Mott insulator?
Electron doped.
3 Dimension. Brinkman-Rice Fermi liquid.
AF with localized carriers.
Micro phase separation: stripes
Organic ET salts.
Metal-insulator transition by tuning U/t.
Possibility of a “spin liquid”.
Doping yields a superconductor.
A second family of HiTc superconductors!

14. Electron doped side: AF persists to x=0.13 and the doped
electrons are localized.
What is the origin of the p-h asymmetry? Hopping of electron on
Cu (d10) is physically different from hopping of a Zhang-Rice
singlet located on the oxygen. One possibility is polaron effect is
stronger on the electron side.

15. J=31 meV
X<0.2 commensurate spin order,
localized hole. (polaron effect?)
0.2<x diagonal stripe with 1 hole
per Ni. (microscopic phase
separation into Ni2+ and Ni3+).
Non-metallic until x=0.9
Now ½ hole per linear distance along
the stripe (2 Cu sites) : mobile charge.
Smaller J means it is deeper in the Mott phase.
Effective hopping is also small and polaron
effects favor localized carriers.

16. Tokura et al, PRL 70, 2126 (1993).
X=0 is a band insulator, x=1 is a Mott insulator.
For x=1, Ti is d1 and has S=1/2. Very small
optical gap (0.2eV). Surprisingly small TN=150K,
(reduced due to orbital degeneracy).
3 dim perovskite structure.
Specific heat = γT

17. This is an example of “Brinkman-Rice Fermi liquid”.
Diverging mass near the Mott insulator. m*/m=1/xh, z=xh.
σ= e^2nτ/m* is proportional to xh , even
though Fermi surface is “large” and has
volume x=1-xh as inferred from the Hall effect.

18. Metal- insulator transition by tuning U/t.
U/t
x
AF Mott insulator
metal
Cuprate superconductor
Organic superconductor
Tc=100K, t=.4eV, Tc/t=1/40.
Tc=12K, t=.05eV, Tc/t=1/40.

19. X = Cu(NCS)2, Cu[N(CN)2]Br,
Cu2(CN)3…..
Q2D organics κ-(ET)2X
anisotropic triangular lattice
dimer model
ET
X
t’ / t = 0.5 ~ 1.1
t’
t t
Mott insulator

20. Q2D antiferromagnet
κ-Cu[N(CN)2]Cl
t’/t=0.75
Is the Mott insulator necessarily an
AF?
“Slater vs Mott”.
Until recently, the experimental
answer is yes.
A digression on spin liquid.

21. Q2D spin liquid
κ-Cu2(CN)3
Q2D antiferromagnet
κ-Cu[N(CN)2]Cl
t’/t=1.06
No AF order down to 35mK.
J=250K.
t’/t=0.75

22. Magnetic susceptibility, Knight shift, and 1/T1T
• Finite susceptibility and 1/T1T at T~0K : abundant low
energy spin excitation (spinon Fermi surface ?)
C nuclear
[A. Kawamoto et al. PRB 70, 060510 (04)]

23. Wilson ratio is approx.
one at T=0.
γ is about 15 mJ/K^2mole
Something happens around 6K.
Partial gapping of spinon Fermi
surface due to spinon pairing?
From S. Yamashita,.. K. Kanoda, Nature Physics, 4,459(2008)

24. More examples have recently been reported.

26. ET2Cu(NCS)2 9K sperconductor ET2Cu2(CN)3 Insulator spin liquid
M. Yamashita ...Matsuda ,Nature Physics 5,44(2009)Belin, Behnia, PRL81,4728(1998)
Thermal conductivity

27. Superconductivity in doped ET, (ET)4Hg2.89Br8, was first discovered Lyubovskaya et al in
1987. Pressure data form Taniguchi et al, J. Phys soc Japan, 76, 113709 (2007).
Doping of an organic Mott insulator.

28. Note the common feature of high Tc and organics:
• Proximity to Mott insulator.
• singlet and d-wave pairing.
Is it possible to have superconductivity in purely
repulsive models, and if so, how do we understand it?
Note that in d-wave pairing, we avoid on-site repulsive
energy. By making singlet pairs, we can gain exchange
energy.

29. 1. The one hole problem.
Theory for t-J model: self consistent Born approx. of hole scattered by AF
magnon works very well. (Kane,Lee and Read, 1989 , Schmitt-Rink et al,….).
Main conclusions: the dispersion is given by an effective hopping of order J. The
hole spectrum has a coherent part with relative spectral weight (J/t) and a broad
incoherent part spreading over t.
ARPES data: review by X. J. Zhou et al, cond-mat0604284)
Not the whole story: line width very broad (300meV) and comparable to
dispersion. To explain this, need to include strong electron phonon
coupling (polaron). Line-shape is interpreted as Franck-Condon effect as
in molecular H2. However, the peak of the spectral function is still given
by the bare dispersion.
Message: one band t-J model works, but need strong e-phonon coupling.

30. Ideal for 2 dim. Assume parallel momentum is
conserved. Measure ejected electron energy
and infer the energy and momentum of the hole
left behind.
Surface sensitive probe.
Resolution a few meV.
Recent Laser ARPES employs VUV lasers
(about 7 eV). Energy resolution 0.26meV.
Deeper penetration. Limited k space coverage.
No tunability.

31. Light Source VUV Laser Synchrotron
Energy Resolution (meV) 0.26 5~15
Momentum Resolution
(Å-1
)
0.0036
(6.994eV)
0.0091
(21.1eV)
Photon Flux(Photons/s) 1014
~1015
1012
-1013
Electron Escape Depth
(A)
30~100 5~10
Photon Energy Tunability Limited Tunable
k-Space Coverage Small Large
Advantages and Disadvantages of VUV Laser ARPES
Laser and Synchrotron are
complementary.

32. Bi2Sr2CaCu2O8+δ
YBCOLSCO
BSCCO or Bi-2212
Simple, x is known,
disorder. Low Tc. Cleanest. Doping by varying
oxygen conc. on chains.
Cleavage plane.
Disorder.
.
Bi-2201
(Bi2Sr2CuO6+x)

33. Eisaki et al, PRB 69,
064512 (2004)
With further increase
of layers, Tc does not
go up further. The
inner planes have less
hole and may be AF
ordered.

34. 2. Small doping.
DC transport.
Boltzmann conductivity:
σ=ne^2τ/m
Ando et al, PRL 87, 017001 (01)
Hall effect:
RH=1/nec
x=0.03 sample, from Padilla et al, PRB72,060511(2005)
Anomalous T dependence.

35. Optical conductivity
Timusk and Statt,Rep Prog Phys 62,61 (99)
Drude formula for simple metal:
Extended Drude formula:
Padilla et al, PRB72,060511(05)
Include high frequency
incoherent part.
From reflectivity or ellipsometry,
deduce Re and Im parts of σ(ω).

36. Conclusion from transport measurements:
No divergent mass enhancement. m*/me~4.
Drude spectral wt (n/m*) is proportional to x with no T
dependence. This wt becomes the superfluid density in the SC.
Scattering rate is roughly 2kT and becomes linear in ω at high
frequencies.
Weight of delta function is
the superfluid density and is
proportional to x

37. Neutron scattering:
If there is long range AF order, Bragg peaks appear at G’s.
The direction of the ordered moment can be determined by rotating G.
In the absence of long range order, we can measure equal time
correlation function by integrating over ω.

38. Local moment picture works.
Reduced from classical moment of
unity due to quantum fluctuations of
S=1/2.

39. NMR Local probe. Does not require large samples.
Very important for the study of new materials.
1. Knight shift. Proportional to spin susceptibility,
but free from impurity contributions. Line is often
broadened by random distribution of local fields.
Need good quality material. The shift and onset of
line broadening can be used to measure spin order.
2. Spin relaxation rate. Measures the low
energy spectrum of spin fluctuations.
3. NQR. Measure local electric field distribution.
χ=χS (T)+ χVV +χcore+χimpurity(T)
K=KS (T) + KVV + Kcore
KS ~ χS KVV ~ χVV
Form factor F(q) peaks at different q for different sites.
For example, planar oxygen site does not see AF q=(π,π),
but Cu site does.
For metals, Korringa relation:

40. One component vs two component system: validity of the one band Hubbard model.
Knight shift on different sites
have identical T dependence.
Takigawa et al PRB43, 247 (91).

41. Theoretically, C. Varma believes that 3 band Hubbard model
with interaction V between Cu and O is needed. He
proposes the existence of orbital currents in the plane
between Cu and O. These currents occur within the unit cell
and does not change the unit cell.
Orbital currents have been observed by
neutron scattering. The onset of these
currents seem related to T*, the pseudo-
gap scale.
However, the moments are about 45
degrees from the plane. Numerical studies
find orbital currents between planar and
apical oxygen. (Weber et al, ArXiv
0803.3983). Perhaps these effects do not
affect the Fermi surface.
Li ..Bourges, Greven, Nature 455, 372 (2008).
There is also reports of T breaking
(ferromagnetic like) by polar Kerr effect
at slightly lower temperature. (Xia,…
Kapitulnik,PRL 100,127002 (08))

42. 3. Properties of the superconductor.
Pairing is d symmetry.
Phase sensitive measurements.
Tsuei and Kirtley Rev Mod Phys 2000.
1. tri-crystal experiment, IBM 1993.
½ flux vortex at the junction.
Standard hc/2e votex
everywhere else.
2. Corner SQUID.
Wollman et al 1993.

43. ARPES. Node along diagonal.
Ding et al Nature 382, 51 1996.
Dirac cone characterized by vF and v∆.

44. Importance of phase fluctuations.
Superfluid stiffness Ks is related to the Drude spectral wt..
It is measured by London penetration depth.
Thermal excitation of nodal qp gives linear T reduction.
Microwave cavity perturbation expt, or by muon precession
relaxation rate which measures the magnetic field
distribution near the vortex. Note very long λ (several
thousand angstrom) implies very small stiffness or
superfluid density.
Uemura plot: linear relation
between Tc and ns/m*.
From Boyce et al, Physica C 341,561 (00)

45. A distribution of magnetic field (eg caused
by the overlapping fields of vortices)
causes a damping of the oscillations.
Another set-up is zero field muSR, which is
very sensitive to static (on the scale of the
muon lifetime of 2 micro-sec) internal
magnetic field (as low as a few gauss) due
to magnetic ordering or spin glass freezing.
+ve Muons relax to certain (often unknown) sites.

46. In 2D phase fluctuations destroy SC order
via the Kosterlitz-Thouless mechanism of
proliferation of vortices and anti-vortices.
They predict a universal relation:
The dynamics of phase fluctuations is probed
by microwave conductivity by Corson et al
Nature 398,221 (1999) in UD Bi-2212 Tc 74K.
(More about fluctuation SC via Nernst effect and diamagnetism later.)
For a SC:
Scaling function: (Ω=1/τ)
Then Tc is controlled by Ks, not
by the energy gap as in BCS
theory. Strong violation of BCS
relation 2∆/kTc~4.

47. Isotope effect.
Summary:
Substantial isotope effect on Tc for underdoped, but
little or no isotope effect for optimal and overdoped.
However, there is isotope effect on ns/m* for all doping.
(unexplained: needs better understanding of e-phonon
in strongly correlated materials.)
On the other hand there is no isotope effect on Fermi
velocity by Laser ARPES, while there is shift in “kink”
energy. (Iwasawa..Dessau,PRL101,157005(08)
m*/m=1+λ, but λ usually has no isotope effect.
Khasanov …Keller, PRB 73,214528 (06)
Qualitatively consistent with the idea
that in UD, Tc is controlled by ns/m*.
If Tc~ns/m*, we expect ∆Tc/Tc=-2∆λ/λ (line Α),
but data is closer to ∆Tc/Tc=-δλ/λ. (line B)
YBCO
However, in practice Tc has a more
complicated dependence on ns/m*.

48. Other probes of nodal quasi-particles:
1. Quasi-particle dispersion shifted by electromagnetic gauge field A.
Volovik (1993) pointed out that near a vortex,
Set R to the average spacing between vortices.
Predicts a specific heat which goes as sqrt(B)
and observed by K. Moler.
2. Universal ac conductivity and thermal
conductivity. ( Lee, 93, Durst and Lee 2000)
Taillefer, PRL 79, 483 (97)
Use to measure v∆/vF.

49. Raman scattering (electronic).
Devereaux and Hackl, Rev Mod Phys 79, 175(2007)
Non-resonant
resonant

50. Probe particle-hole charge excitation with a form factor.
Expand the polarization tensor in terms of irreducible representation
of lattice point symmetry. For square lattice:
γ(k)=
γ(k)=

51. Expected contribution
from quasi-particle,
quasi-hole excitation.
The initial slope is proportional to τ.
The broad continuum comes from
incoherent electronic excitations.

52. Summary:
The superconducting state is singlet d-wave pairing. The nodes dominate
low temperature properties and are well characterized.
In the underdoped region, Tc is determined by phase fluctuation and not
by the vanishing of the pairing gap. As a result, the energy gap is large
even though Tc is small.
While unusual, a lot of the physical properties of the superconducting
state at low temperature can be understood based on a conventional
physical picture.
As we will see, questions remain as to what happens at higher
temperature above Tc and in a high magnetic field which restores the
resistive state. Furthermore, the precise behavior of the gap near the
anti-node (0,π) remains to be clarified.