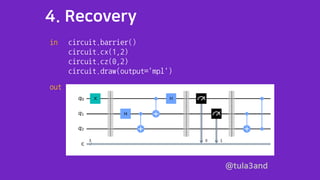
The document describes a presentation on quantum teleportation utilizing Qiskit, featuring instructions for implementing quantum circuits and performing measurements. It outlines the no-cloning theorem, creation of entangled qubits, and the recovery process through specific circuit operations. Additionally, the document includes references for further reading and encourages audience interaction.

1. Quantum
Teleportation
With Qiskit
20201031
Presented by Dayeong, Kang
Designed by Dayeong, Kang

2. A B
@tula3and

3. A B
@tula3and
No-cloning Theorem

4. A B
@tula3and
T
Classical Bit
Entangled Qubits

5. A B
@tula3and
T
Classical Bit
Entangled Qubits

6. @tula3and
A
B
|Ψ>
Bell
State
Measurement
Recovery |Ψ>

7. @tula3and
A
B
|Ψ>
Bell
State
Measurement
Recovery |Ψ>
|00> Apply I
|01> Apply X
|10> Apply Z
|11> Apply ZX

8. @tula3and
Let’s start coding
Open jupyter notebook

9. @tula3and
0. Check the Qiskit version
import qiskit
qiskit.__qiskit_version__
{'qiskit-terra': '0.16.0',
'qiskit-aer': '0.7.0',
'qiskit-ignis': '0.5.0',
'qiskit-ibmq-provider': '0.11.0',
'qiskit-aqua': '0.8.0',
'qiskit': '0.23.0'}
in
out

10. @tula3and
1. Make a state for A
from qiskit import *
circuit = QuantumCircuit(3, 3)
circuit.x(0)
circuit.barrier()
%matplotlib inline
circuit.draw(output='mpl')
in out

11. @tula3and
2. Bell State (1)
circuit.h(1)
circuit.cx(1,2)
circuit.draw(output='mpl')
in
out

12. @tula3and
2. Bell State (2)
circuit.cx(0,1)
circuit.h(0)
circuit.draw(output='mpl')
in
out

13. @tula3and
3. Measurement
circuit.barrier()
circuit.measure([0,1],[0,1])
circuit.draw(output='mpl')
in
out

14. @tula3and
3. Measurement
circuit.barrier()
circuit.measure([0,1],[0,1])
circuit.draw(output='mpl')
in
out
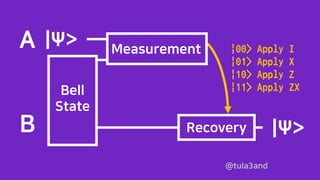
|00> Apply I
|01> Apply X
|10> Apply Z
|11> Apply ZX

15. @tula3and
4. Recovery
circuit.barrier()
circuit.cx(1,2)
circuit.cz(0,2)
circuit.draw(output='mpl')
in
out

16. @tula3and
5. Check the B state
circuit.measure(2,2)
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend = simulator, shots = 1024).result()
counts = result.get_counts()
from qiskit.tools.visualization import plot_histogram
plot_histogram(counts)
in
out

17. @tula3and
References
1. Qiskit textbook; Quantum Teleportation
2. Coding with Qiskit; Quantum Teleportation
3. Quantum teleportation by Michael Nielsen

18. @tula3and
Thank you for listening
Any Questions?