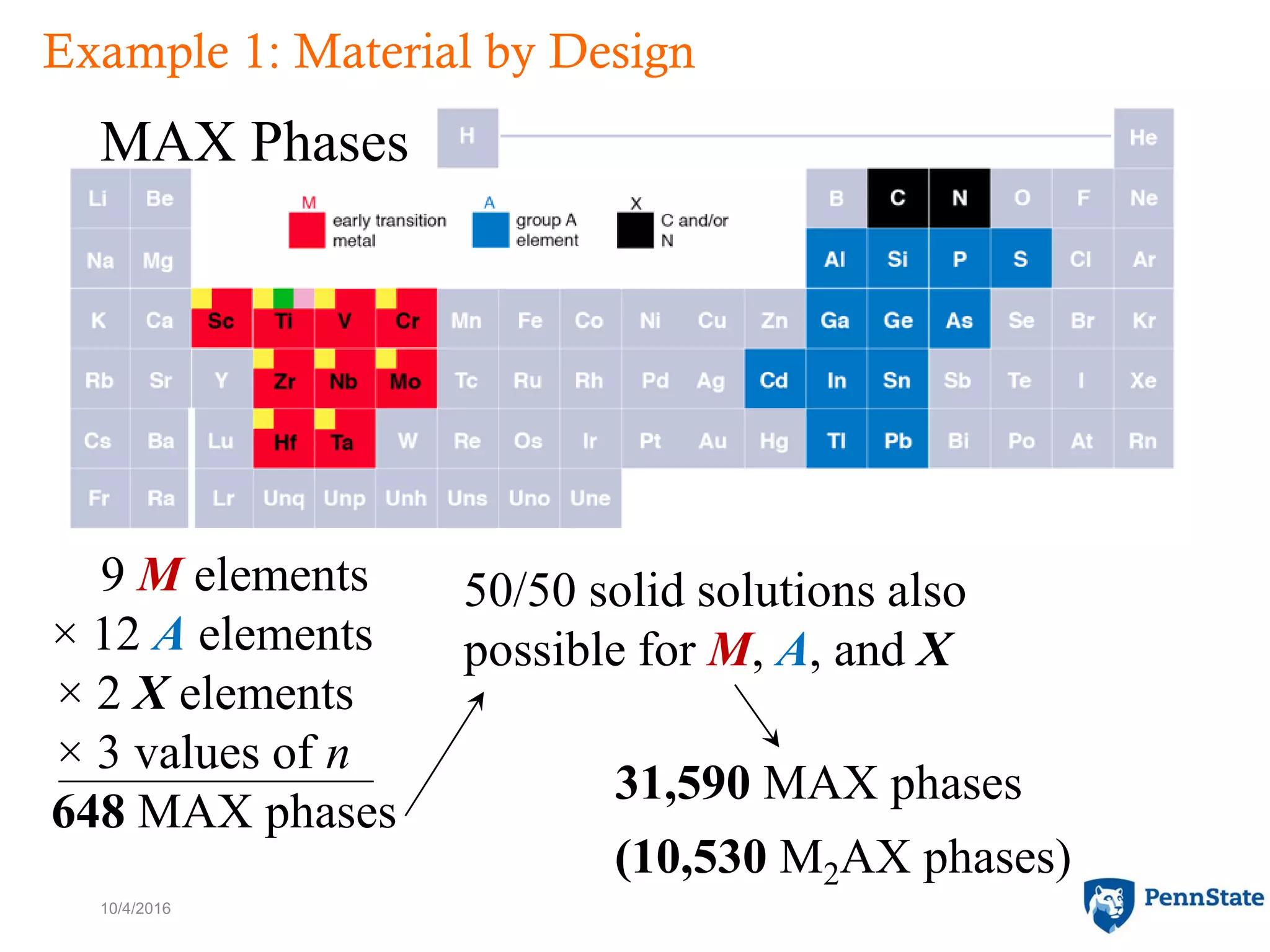
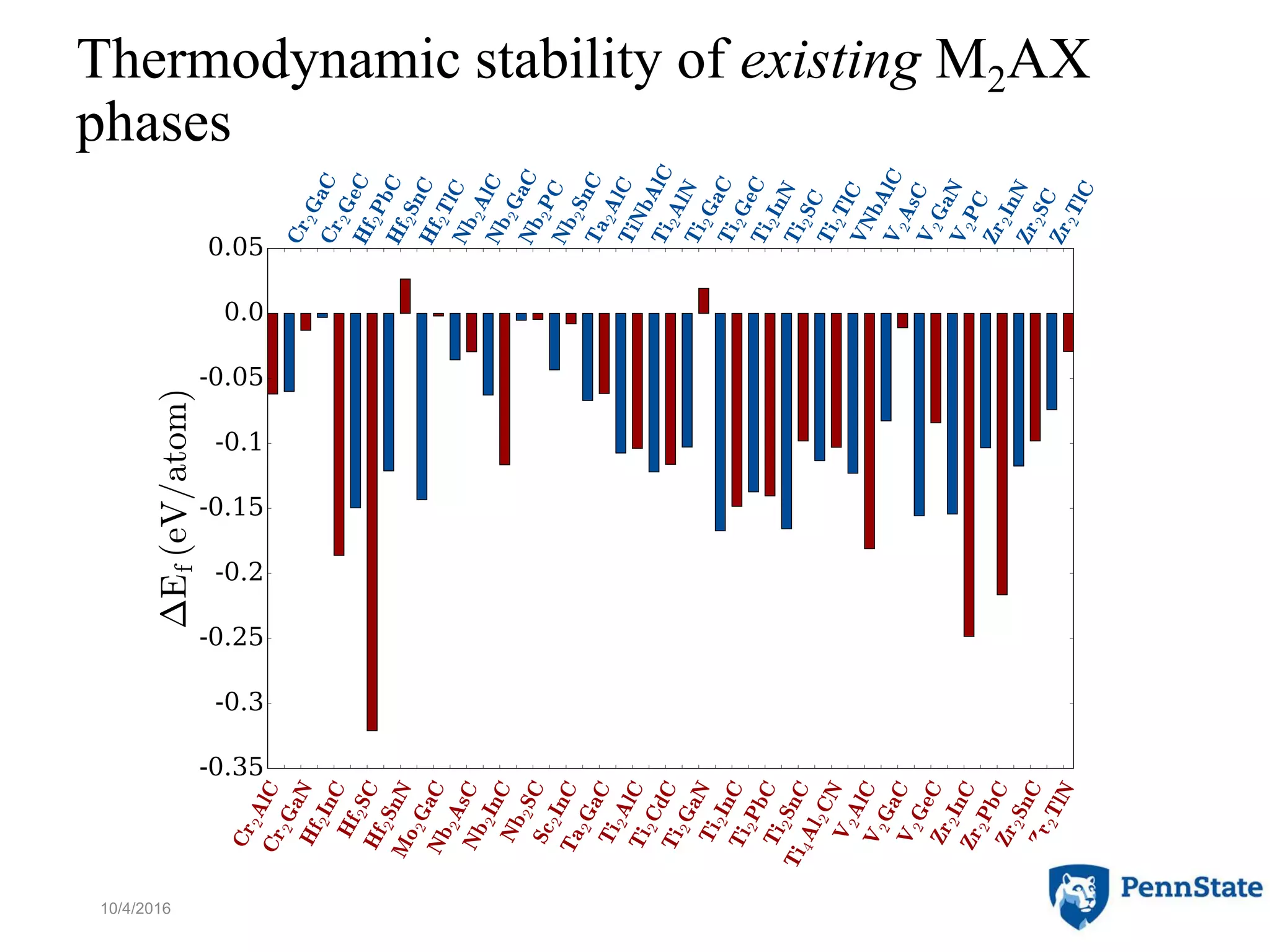
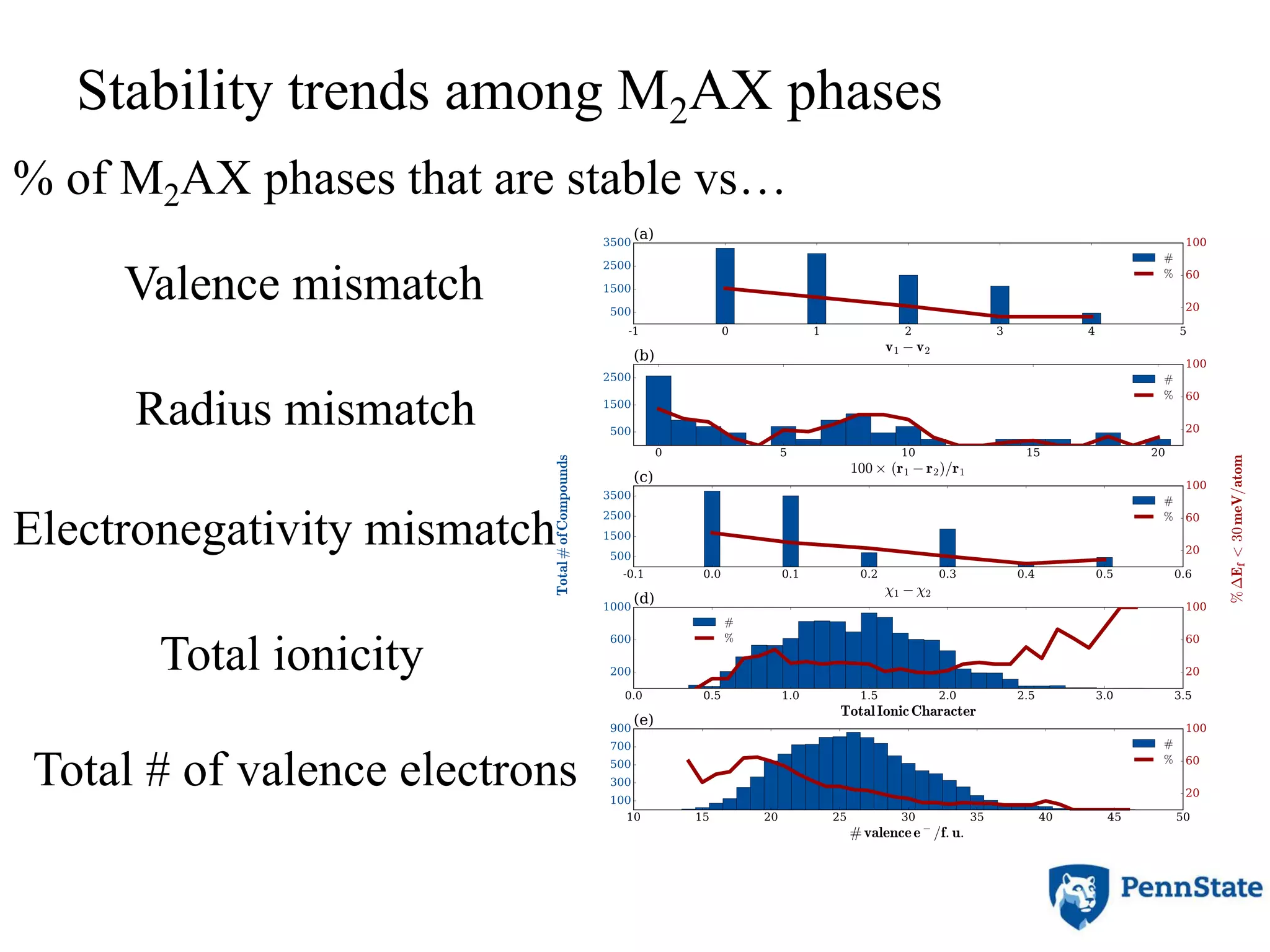
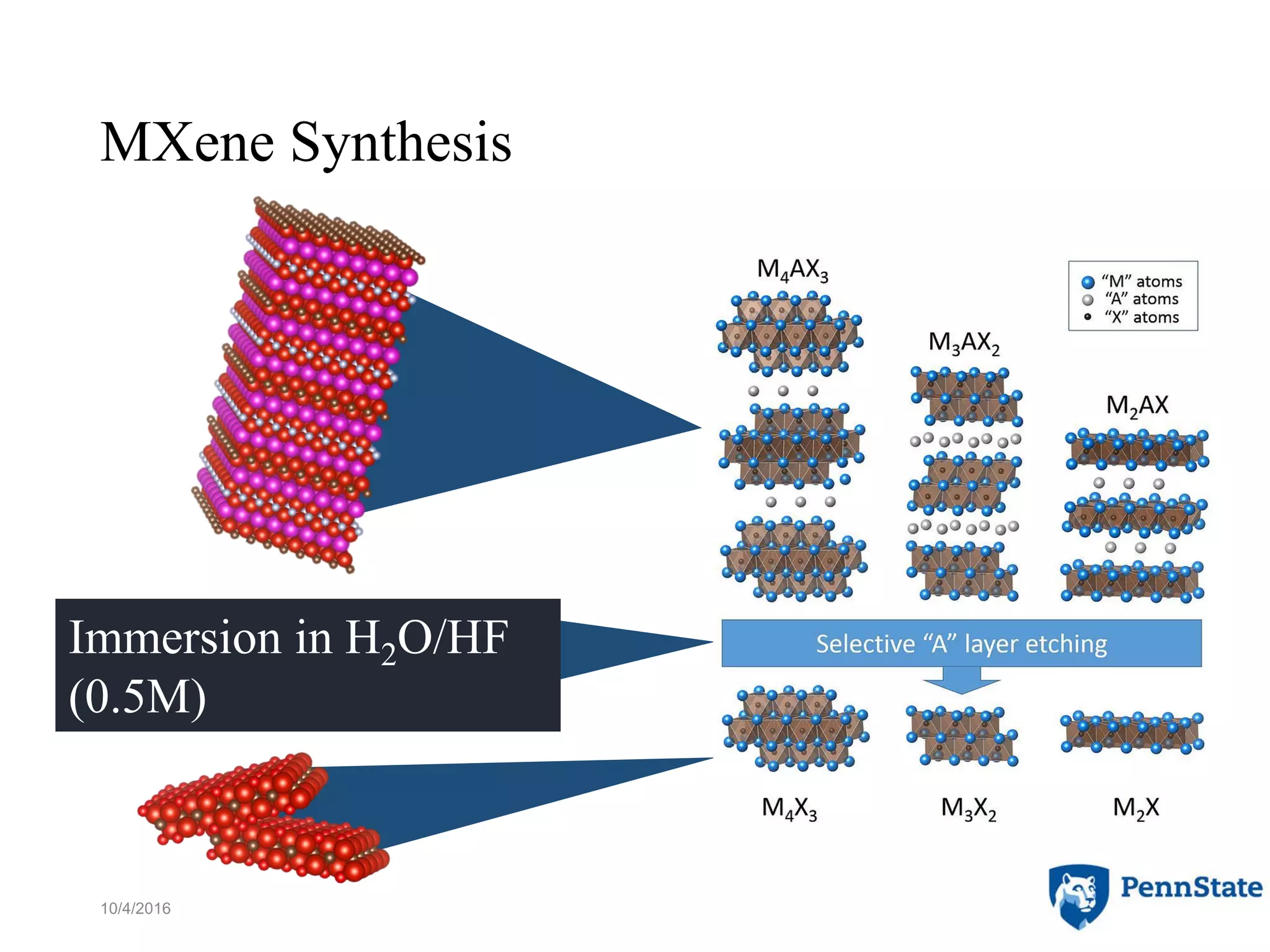
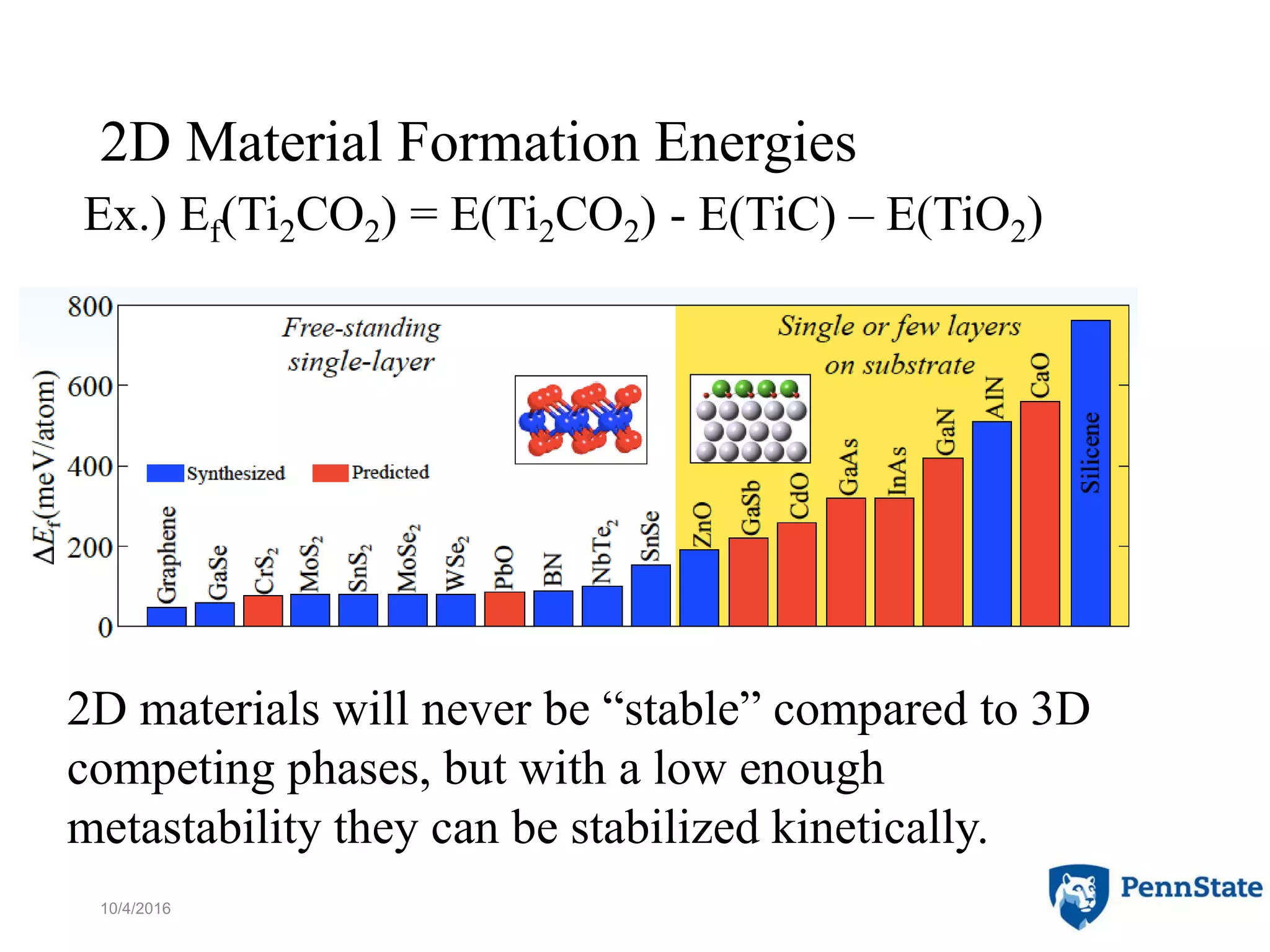
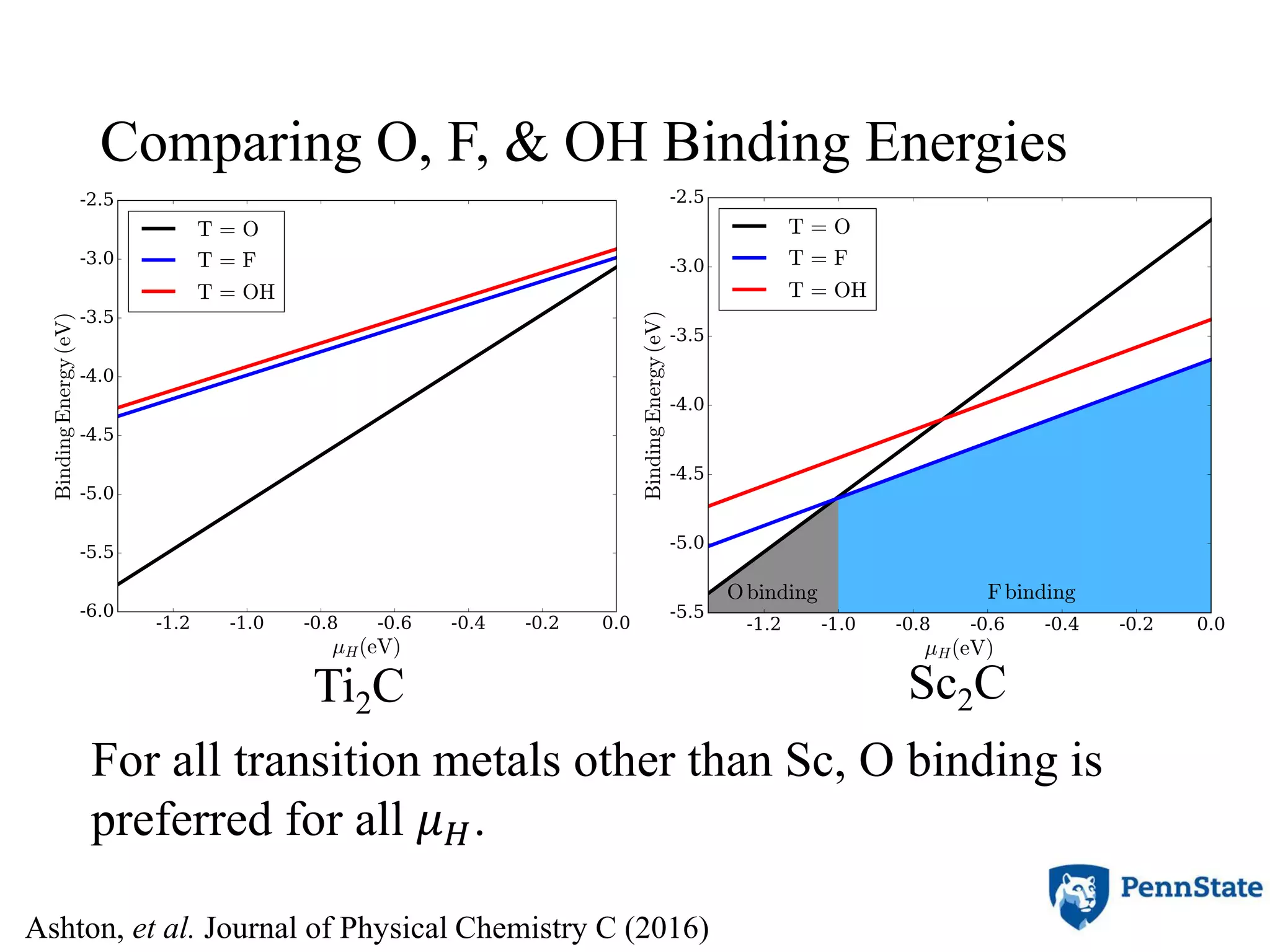
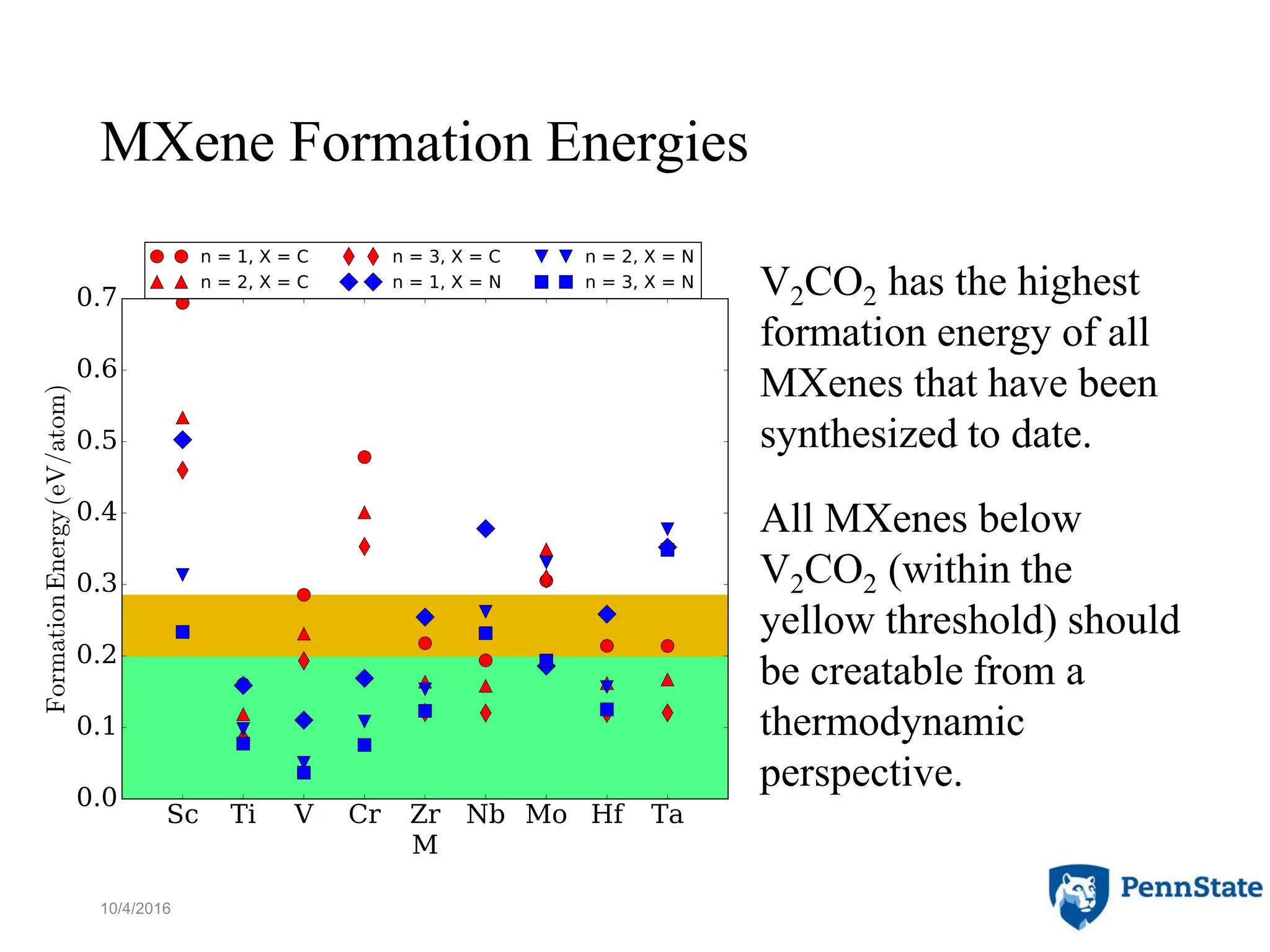
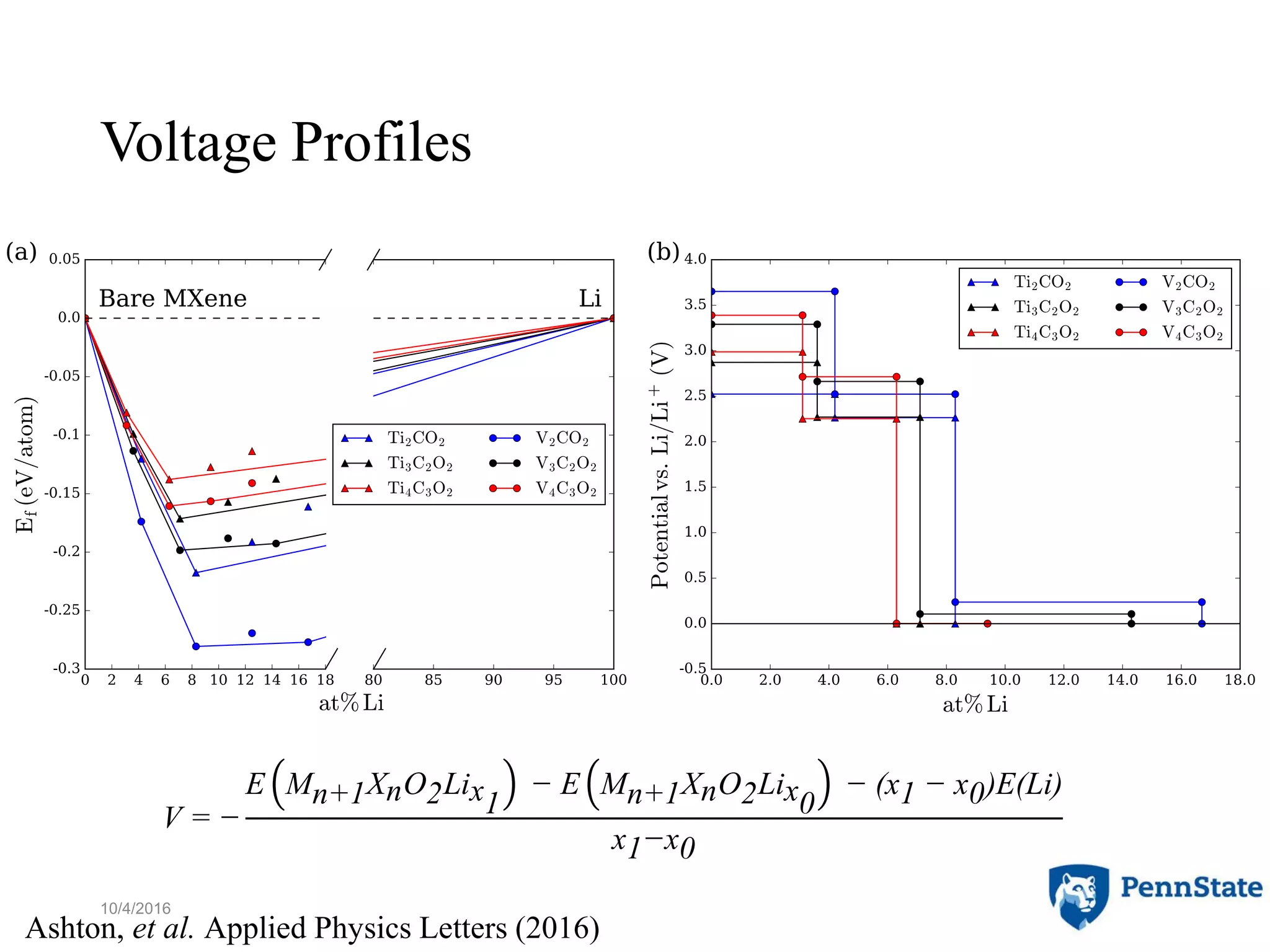
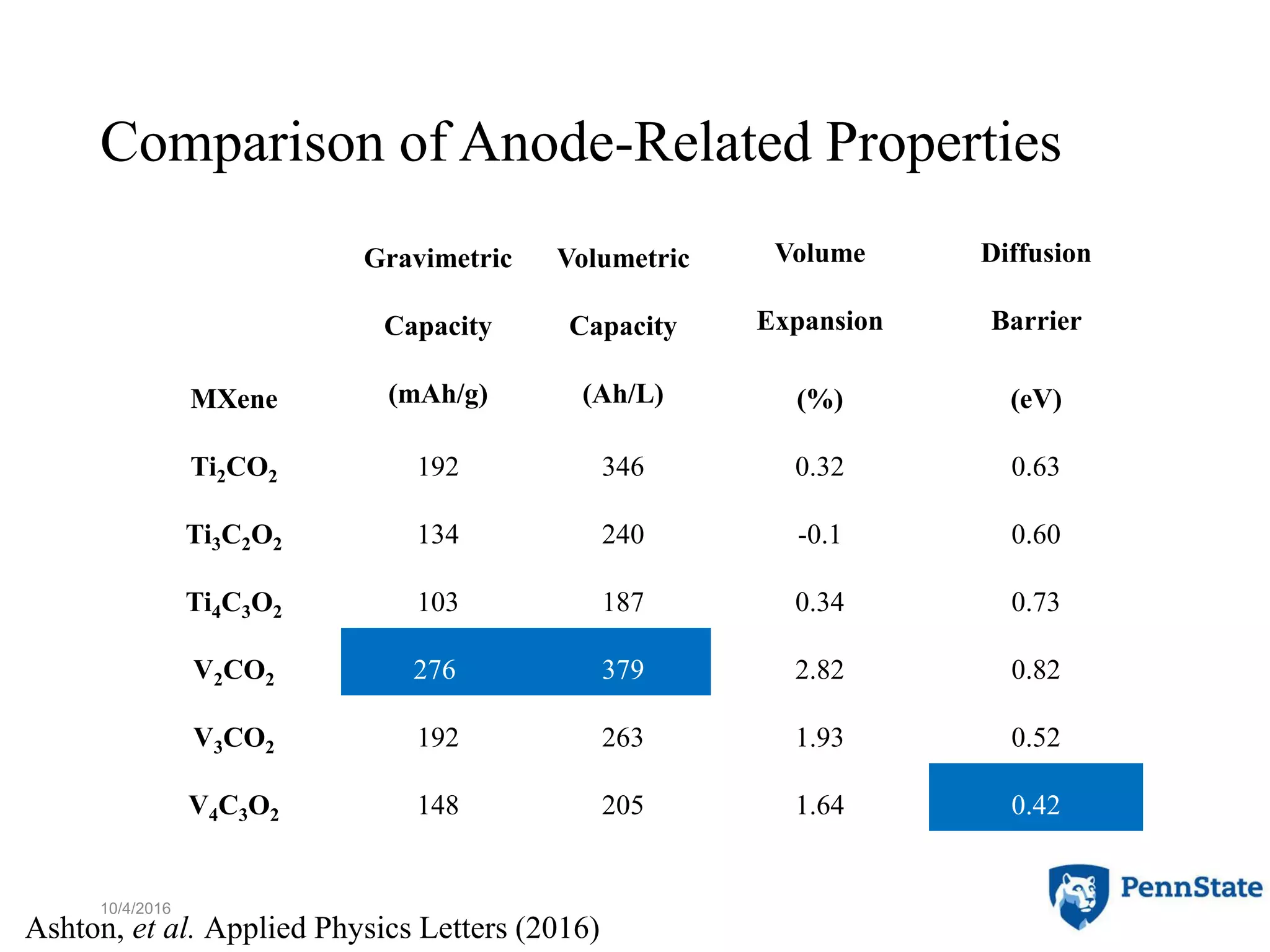
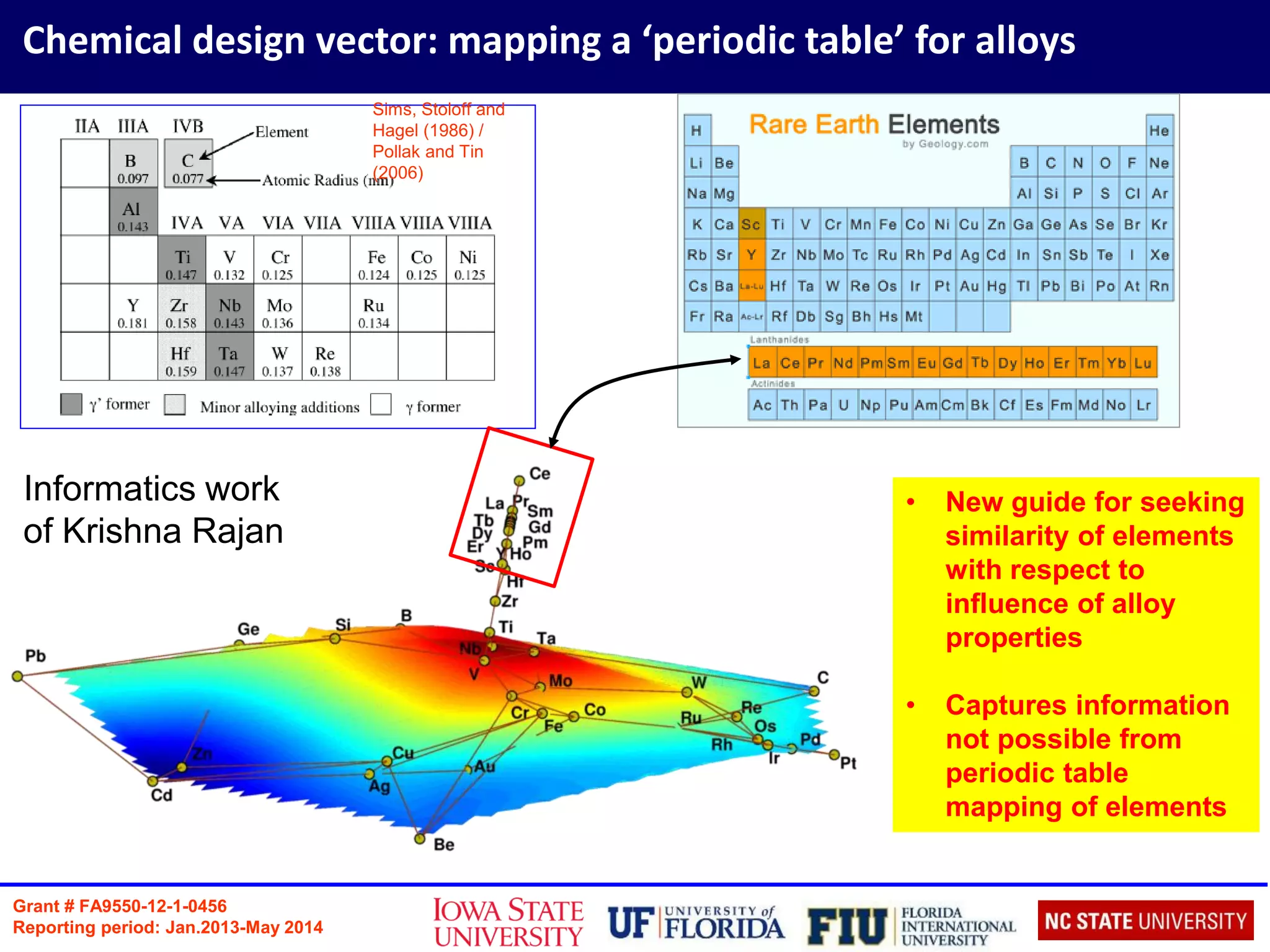
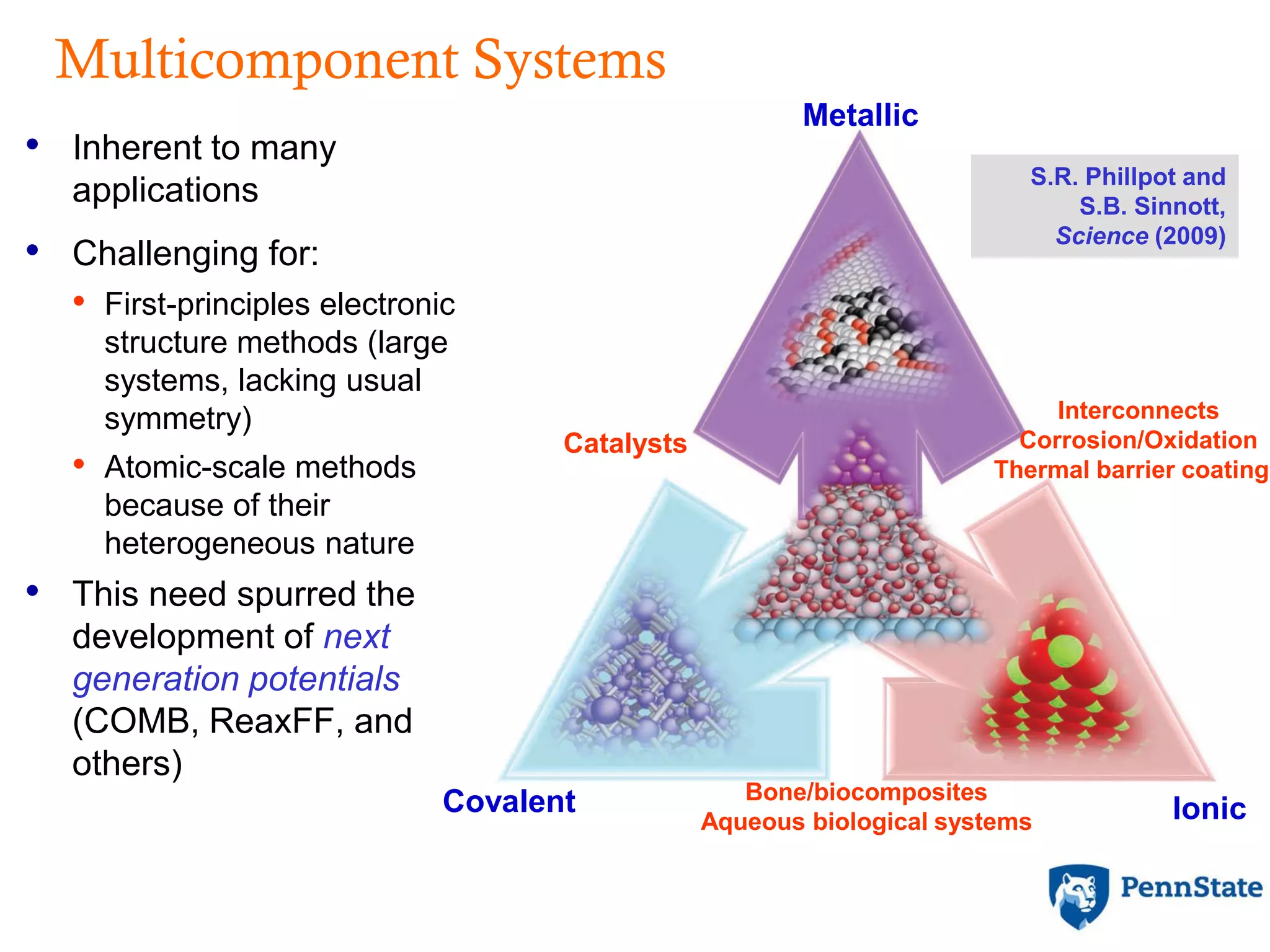
The document discusses the role of atomic-scale modeling in materials design and discovery, highlighting the use of high fidelity computational methods such as quantum chemical approaches and density functional theory. It explores various applications, including the design of M2AX phases, MXenes for battery anodes, and alternatives to rare earth metals in superalloys, emphasizing the importance of understanding fundamental atomic behaviors to inform broader scale models. Additionally, it addresses challenges in predictive modeling, the integration of computational approaches with experimental data, and the need for efficient cyberinfrastructure to facilitate materials research.

1. Role of Atomic-Scale Modeling in
Materials Design Discovery
Susan B. Sinnott
Department of Materials Science and Engineering
Penn State University
University Park, PA
XV Brazil MRS Meeting
September 27, 2016

2. Materials State Awareness with Atomic and
Nanometer Scale Computational Methods
• Electronic-structure level
• High fidelity methods available:
• Quantum chemical approaches
• Density functional theory (DFT)
• Off-the-shelf codes widely available
• Wide-spread understanding of strengths and limitations
Atomic-scale level
Many-body, realistic potentials have been available for over 30 years
Ideal for examining systems under extreme environments
Necessary to investigate chemistry + microstructure + mechanics +
mechanisms + …..
Physics-based model development
Inform microscale and mesoscale models
Explain experimental observations (strong “suggestion about
what the atoms are doing”)

3. MAX Phases
10/4/2016
9 M elements
× 12 A elements
× 2 X elements
× 3 values of n
648 MAX phases
50/50 solid solutions also
possible for M, A, and X
31,590 MAX phases
(10,530 M2AX phases)
Example 1: Material by Design

4. Thermodynamic stability of existing M2AX
phases
10/4/2016 4

5. Stability trends among M2AX phases
5
Valence mismatch
Radius mismatch
Electronegativity mismatch
Total ionicity
Total # of valence electrons
% of M2AX phases that are stable vs…

6. Magnetic M2AX Phases
Cr2InN & Cr4(CdIn)N2 show ferromagnetic ordering at 0K
10/4/2016 6
Cr2InN Cr4(CdIn)N
Formation
energy
(meV/atom)
7 21
Magnetization
energy (meV/Cr
atom)
68 70
Final magnetic
moment
(μB/Cr atom)
1.08 1.18

7. MXene Synthesis
10/4/2016 7
Immersion in H2O/HF
(0.5M)

8. 2D Material Formation Energies
10/4/2016 8
Ex.) Ef(Ti2CO2) = E(Ti2CO2) - E(TiC) – E(TiO2)
2D materials will never be “stable” compared to 3D
competing phases, but with a low enough
metastability they can be stabilized kinetically.

9. Comparing O, F, & OH Binding Energies
9
Eb = E Mn+1XnTm – E Mn+1Xn –
m
2
E T2 – mμT
Coated MXene
Bare MXene
Surface species reference
Surface species chemical potential
μO = ΔG
f
H2O
− 2μH
μOH = ΔG
f
H2O
−μH
μF = ΔGf
HF− μH
All depend on μH
Ashton, et al. Journal of Physical Chemistry C (2016)

10. Comparing O, F, & OH Binding Energies
10
Ti2C Sc2C
For all transition metals other than Sc, O binding is
preferred for all 𝜇 𝐻.
Ashton, et al. Journal of Physical Chemistry C (2016)

11. MXene Formation Energies
10/4/2016 11
V2CO2 has the highest
formation energy of all
MXenes that have been
synthesized to date.
All MXenes below
V2CO2 (within the
yellow threshold) should
be creatable from a
thermodynamic
perspective.

12. Li-Ion Battery Anode Candidate Criteria
•Stable
•Lightweight
•Inexpensive
•High capacity
•Low diffusion barrier
•Minimal swelling during charge/discharge
10/4/2016 12
Tin+1CnO2 & Vn+1CnO2

13. Diffusion Pathways in Multilayer MXenes
10/4/2016 13
O (over)O (under) Li
(a) (b)
[0100]
[1000]
a
b
[1200]
[1100]
Monolayer Multilayer
ΔE (eV)
1.0
2.0
3.0
4.0

14. Voltage Profiles
10/4/2016 14
V = −
E Mn+1XnO2Lix1
− E Mn+1XnO2Lix0
− (x1 − x0)E(Li)
x1−x0
Ashton, et al. Applied Physics Letters (2016)

15. Comparison of Anode-Related Properties
10/4/2016 15
MXene
Gravimetric
Capacity
(mAh/g)
Volumetric
Capacity
(Ah/L)
Volume
Expansion
(%)
Diffusion
Barrier
(eV)
Ti2CO2 192 346 0.32 0.63
Ti3C2O2 134 240 -0.1 0.60
Ti4C3O2 103 187 0.34 0.73
V2CO2 276 379 2.82 0.82
V3CO2 192 263 1.93 0.52
V4C3O2 148 205 1.64 0.42
Ashton, et al. Applied Physics Letters (2016)

16. Example 2: Nickel-Based Superalloy Design
BRI: Searching for RE Alternative
through Crystal Engineering
• Used in high temperature-
applications such as gas-turbines1
• Two phases present:
γ- Ni matrix
γ’- Ni3Al (~ 70% volume)
Microstructure of γ-γ’ phases of Ni
single crystal superalloys2
L12 – Al at
corners, Ni at
face-centers
1. R Schafrik and R Sprague; Adv. Mat. and Proc. 162 (2004)
2. P Caron and O Lavigne; J. Aerospace Lab. 3 (2011)
Objective: Identify alternative, earth-
abundant alternatives to rare earth
metals in Ni-based superalloys

17. BRI: Searching for RE Alternative
through Crystal Engineering
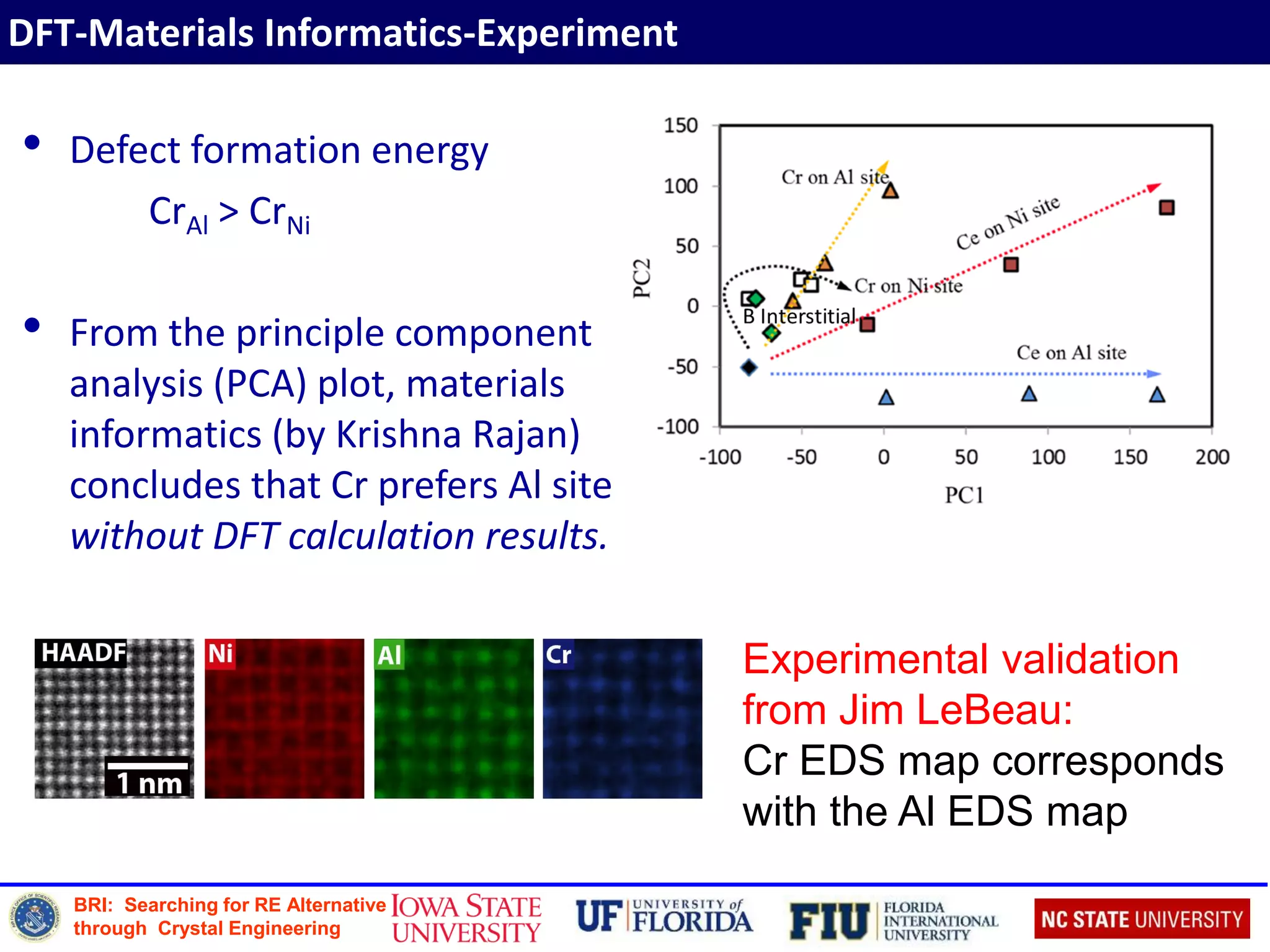
Defect Formation Energy
Defect formation energy of incorporating dopant X is defined as:
Etot[Xq] = total energy of the system with the defect
Etot[bulk] = total energy of the system without the defect
n = number of atoms added (n > 0) or removed (n < 0)
μi = chemical potential of species i
X Ef (XAl) (eV) Ef (XNi) (eV)
B 2.60 0.87
Cr 1.40 (1.351) 0.93 (0.921)
Ce 0.81 1.81
Zr 0.10 (0.041) 0.31 (0.201)
1. D E Kim, S L Shang, Z K Liu; Intermetallics 18 (2010)

18. BRI: Searching for RE Alternative
through Crystal Engineering
DFT-Materials Informatics-Experiment
• Defect formation energy
CrAl > CrNi
• From the principle component
analysis (PCA) plot, materials
informatics (by Krishna Rajan)
concludes that Cr prefers Al site
without DFT calculation results.
Experimental validation
from Jim LeBeau:
Cr EDS map corresponds
with the Al EDS map

19. Chemical design vector: mapping a ‘periodic table’ for alloys
Grant # FA9550-12-1-0456
Reporting period: Jan.2013-May 2014
Sims, Stoloff and
Hagel (1986) /
Pollak and Tin
(2006)
• New guide for seeking
similarity of elements
with respect to
influence of alloy
properties
• Captures information
not possible from
periodic table
mapping of elements
Informatics work
of Krishna Rajan

20. Materials State Awareness with Atomic and
Nanometer Scale Computational Methods
• Electronic-structure level
• High fidelity methods available:
• Quantum chemical approaches
• Density functional theory (DFT)
• Off-the-shelf codes widely available
• Wide-spread understanding of strengths and limitations
• Atomic-scale level
• Many-body, realistic potentials have been available for over 30 years
• Ideal for examining systems under extreme environments
• Necessary to investigate chemistry + microstructure + mechanics +
mechanisms + …..
• Physics-based model development
• Inform microscale and mesoscale models
• Explain experimental observations (strong “suggestion about
what the atoms are doing”)

21. 30 Years of Many-Body Atomic-Scale
Potentials (Reactive Force Fields)
May 2012 issue
Historically developed for materials
with specific types of chemical bonds
 Tersoff potentials for Si
 Brenner or REBO potential for C,H
+ O,F,S,….
 AIREBO
 EAM potentials for metals
 MEAM for metals and oxides
 EAM+ES for metals and oxides
 Rigid ion (Buckingham) potentials for
ionically bound materials
Used to examine phenomena at the
atomic and nanometer scale and
develop a qualitative, mechanistic
understanding

22. Metallic
IonicCovalent Bone/biocomposites
Aqueous biological systems
Interconnects
Corrosion/Oxidation
Thermal barrier coatings
Catalysts
Multicomponent Systems
• Inherent to many
applications
• Challenging for:
• First-principles electronic
structure methods (large
systems, lacking usual
symmetry)
• Atomic-scale methods
because of their
heterogeneous nature
• This need spurred the
development of next
generation potentials
(COMB, ReaxFF, and
others)
S.R. Phillpot and
S.B. Sinnott,
Science (2009)

23. Example 3: Cu (001)/a-SiO2 Interfaces
Structural properties of the interface
Oxidation of Cu is limited to the first two Cu layers; formation of Cu2O
Type of interface
W (J/m2) Cu-O
(%)Exp COMB
Cu/a-SiO2 + 0 VO
0.5 - 1.2 a
0.6 - 1.4 b
1.810 22
Cu/a-SiO2 + 10 VO 0.629 13
Cu/a-SiO2 + 20 VO 0.289 11
a Oh, et al., J. Am. Ceram. Soc. (1987)
b Pang and Baker, J. Mater. Res. (2005)
• Cu-O bonds play crucial roles in adhesion
of the interface
• Adhesion of Cu/dielectric layer decreases
with O defects
Introduced O vacancies at the interface
0, 10 and 20 VO

24. Charge Transfer Across the Interface
DFT: Nagao et al., COMB: Shan et al.
-10 0 10
-0.020
-0.015
-0.010
-0.005
0.000
0.005
0.010
0.015
0.020
<n(D)>(A
-3
)
Distance (angstrom)
COMB

25. BRI: Searching for RE Alternative
through Crystal Engineering
Example 4: Deformation of metals - Ni
dislocations within grains are generated and
evolve over time
grain are in the BCC arrangement
Common
neighbor analysis
Polycrystalline Ni after being
subjected to tensile test with
constant strain rate (=4x10-9 s-1)
1. A. Kumar, T. Liang, A. Chernatynskiy, Z. Lu, M. Noordhoek, K. Choudhary, S.R. Phillpot, S.B. Sinnott; J. Phys.:
Condensed Matter (in preparation)
2. Y. Mishin, D. Farkas, M.J. Mehl, D.A. Papaconstantopoulos; Phys. Rev. B 59 (1999)
Stacking fault energies:
<112> and <101>
COMB Ni potential1 EAM Ni potential2
Stacking fault energy of Ni1
compared with EAM2 potential
Centro-symmetry analysis

26. BRI: Searching for RE Alternative
through Crystal Engineering
Al deformation predicted by different potentials
COMB Al potential1
EAM Al potential2 Stacking fault energies:
<112> and <101>
Stacking fault energy of Al1
compared with EAM2 potential
1. A. Kumar, T. Liang, A. Chernatynskiy, Z. Lu, M. Noordhoek, K. Choudhary, S.R. Phillpot, S.B. Sinnott; J. Phys.:
Condensed Matter (in preparation)
2. Y. Mishin, D. Farkas, M.J. Mehl, D.A. Papaconstantopoulos; Phys. Rev. B 59 (1999)
Potential energy surface
illustrating the <112> barrier
to be less than the <101>
barrier1

27. BRI: Searching for RE Alternative
through Crystal Engineering
Mechanical deformation of Ni3Al at the g/g’ interface
1. A. Kumar, T. Liang, A. Chernatynskiy, Z. Lu, M. Noordhoek, K. Choudhary, S. R. Phillpot, S.B. Sinnott (in
preparation)
2. M.H. Yoo, M.S. Daw, M.I. Baskes, V. Vitek, D.J. Srolovitz, Eds.; New York: Plenum Press; 1989. p. 401.
Thermostat
Active
Rigid moving
Rigid moving
Thermostat
Active
Ni3Al
Ni
τzx
Z
[010]
X
[101]
Y
[10 -1]
τzx
• Edge dislocations at the Ni-Ni3Al interface
• Predict mechanisms associated with
applied shear stress and dislocation
motion
Ni3Al Ec
(eV/atom)
B
(GPa)
G
(GPa)
COMB1 -4.61 198 93
exp.2 -4.62 195 96
Simulation box size:
16.67x16.67x9.21 nm3
Total number of
atoms: 179,600
Dislocation

28. Technical Fundamental Barriers
• Parameterization of transferrable, next-generation potentials is non-
trivial. For some historical potentials, numerous parameterizations exist.
The general equation for COMB is:
.
• Validation of predicted trends and quantification of error bars.
• Comfort within the broader community of how and when potentials work
well and when the transferability of parameterized properties breaks
down. The materials community is familiar with strengths and limitations
of electronic structure calculations and continuum level (e.g., finite-
element level modeling). Non-experts are less comfortable with atomic-
scale methods.
• Dissemination is straightforward, maintenance is challenging!
   






i
ij
vdW
ji
polar
ij
jikijiiijiijiji
S
iT rEriqErCqBqqrVqEE )(),(),()(,,
2
1
)( 

29. Databases and cyberinfrastructure
• Enable the rapid design of materials
• Materials Project (MIT)
• AFLOWLIB (Duke)
• CAVS CyberDesign (Mississippi State)
• Readily access computational tools and data
• nanoHUB (Purdue)
• CAMS (Florida)
• Improve atomic-scale methods
• NIST Interatomic Potentials Repository Project
• OpenKIM (Minnesota)
• Navigating materials cyberinfrastructures
• TMS

30. Challenges and needs that will shape future directions
• Big-picture challenges:
• What is the role of theory/computational modeling in the design,
processing, and application of materials?
• How do we integrate the latest computational approaches with
experimental data to improve predictability?
• To what extent are computational methodologies available that are
applicable to the physics of interest in actual systems (materials, length and
time scales)?
• How do we ensure the next generation of scientists and engineers can work
in this new paradigm?
• What is needed:
• Natural workflow from discovery codes to predictive software
• Tight integration between processing, characterization, and computational
approaches
• Accurate error bars for the results of theoretical/computational method
results
• Widespread dissemination of software with robust documentation