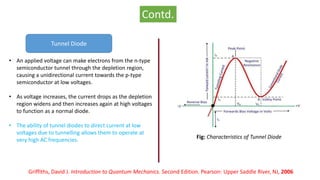
Quantum tunnelling is a quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. Friedrich Hund first used quantum tunnelling to explain molecular spectra in 1927. George Gamow first applied it to calculate alpha decay in 1928. Max Born recognized it as a general result of quantum mechanics. Important applications include scanning tunneling microscopes, tunnel diodes, and the Josephson effect in superconductors. Recent research has explored tunnelling in other systems and potential uses in quantum computing.

1. TUNNELLING IN QUANTUM MECHANICAL SYSTEM
Department of Chemistry
School of Chemical Sciences and Pharmacy
CENTRAL UNIVERSITY OF RAJASTHAN
Bandar Sindri, Ajmer- 305801
Submitted to:
Dr. Jony Saha
Assistant Professor
Central University of Rajasthan
Presentation by:
Soham Thakur
Integrated M.Sc. B.Ed. Chemistry
2018IMSBCH014

2. INTRODUCTION
Quantum Tunnelling
 Quantum mechanical phenomenon
 Observed in microscopic particles such as electron
 A subatomic particle’s probability disappears from one
side of a potential barrier and appears on the other
side without any probability current appearing inside
the well.
 Occurs in all quantum systems.
 Crucial for nucleosynthesis in stars.
Fig: Representation of Tunnelling in a generalised way
Merzbacher, E., Physics Today, 2002, 55(8), 44–49.

3. HISTORY
Friedrich Hund George Gamow
1927 1928
First to use quantum mechanical
barrier penetration in discussing the
theory of molecular spectra
Fig 1: Double Potential well by Hund
showing that Levels 2 and 3 are
characteristically quantal and occupy
both wells, with tunnelling through
the barrier
First application of the effect by mathematical
calculation of the alpha decay
Fig 2: 1D potential used
by George Gamow to
illustrate the tunnelling
of alpha particles
F. Hund, Z. Phys., 1927 40, 742 G. Gamow, Z. Phys., 1928, 51, 204.

4. Max Born
1929
Contd.
Tunnelling, not
restricted
to nuclear physics
but, a general
result of quantum
mechanics that
applies to many
different systems.
Recognizes the
generality of
tunnelling.
Nobel Prize for
Tunnelling
1973
Leo Esaki
Ivar GiaeverBrian Josephson
www.nobleprize.org

5. Mathematical Discussion
0
32
V
1
Lx
E (Particle energy)
Fig: Representation of a 1D potential barrier
which will be penetrated by the particle
(Barrier Potential)
Schrödinger equation yields two different
differential equations depending on the
region:
Region 1 & 3:
Region 2:
The general solutions can be written as:
:Region 1
:Region 2
:Region 3
Griffiths, David J. Introduction to Quantum Mechanics. Second Edition. Pearson: Upper Saddle River, NJ, 2006

6. Contd.
Transmission coefficient for the particle tunnelling across, is calculated using the solution of the Schrödinger eqation and is given
as:
Fig: These graphs shows a localized wavefunction tunnelling through the one-dimensional barrier by evolving the time-
dependent Schrödinger equation
Griffiths, David J. Introduction to Quantum Mechanics. Second Edition. Pearson: Upper Saddle River, NJ, 2006

7. APPLICATIONS
Scanning Tunnelling Microscope
• Extremely sharp tip of only a single-atom-thick
runs over the surface of the material, with the
tip at a higher voltage than the material.
• Voltage allows tunnelling current to flow from
electrons that tunnel from the surface of the
material, through the potential barrier
represented by the air, to the tip of the
microscope, completing a circuit.
• Basis of detection is amount of current.
Griffiths, David J. Introduction to Quantum Mechanics. Second Edition. Pearson: Upper Saddle River, NJ, 2006

8. Tunnel Diode
Contd.
• An applied voltage can make electrons from the n-type
semiconductor tunnel through the depletion region,
causing a unidirectional current towards the p-type
semiconductor at low voltages.
• As voltage increases, the current drops as the depletion
region widens and then increases again at high voltages
to function as a normal diode.
• The ability of tunnel diodes to direct current at low
voltages due to tunnelling allows them to operate at
very high AC frequencies.
Fig: Characteristics of Tunnel Diode
Griffiths, David J. Introduction to Quantum Mechanics. Second Edition. Pearson: Upper Saddle River, NJ, 2006

9. Josephson effect
• In superconductors, at certain temperature ranges
a current can flow indefinitely without resistive
heating occurring.
• In Josephson junctions, two superconducting
semiconductors are separated by a thin insulating
barrier.
• In the Josephson effect, superconducting pairs of
electrons tunnel through this barrier to carry the
superconducting current through the junction.
Contd.
Fig: Characteristics of Josephson Effect
Griffiths, David J. Introduction to Quantum Mechanics. Second Edition. Pearson: Upper Saddle River, NJ, 2006

10. ADVANCEMENT
Substrate imprinted universal sensors and sensors
having nano-tunnelling effect Quantum Tunnelling of water
Tunneling effect in the heterogeneously-
catalyzed formic acid dehydrogenation
Self-aligned tunnelling field effect transistors
Tunnel field-effect transistor with reduced trap-
assisted tunnelling leakage
Kolesnikov, Alexander I.; et. al, Physical Review Letters.. 2016, 116 (16): 167802
Zhou, Y., US Patent, US10495637B2, 2020 Vasen, T., et. al., US20200006542A1, 2020
Song Y., et. al., US20200119168A1, 2019 Mori, K., et. al., Nature Comm., 2019, 10(4094)

11. CONCLUSION
The phenomenon of tunnelling, which has no counterpart in classical physics, is an important
consequence of quantum mechanics.
It has enormous number of applications in the phenomenonal science as well as in instruments
like Diode, Transistor, etc.
Efforts need to improvise quantum computing, and innovation of a quantum computer of
which tunnelling effect will be a huge landmark.

12. Thank You