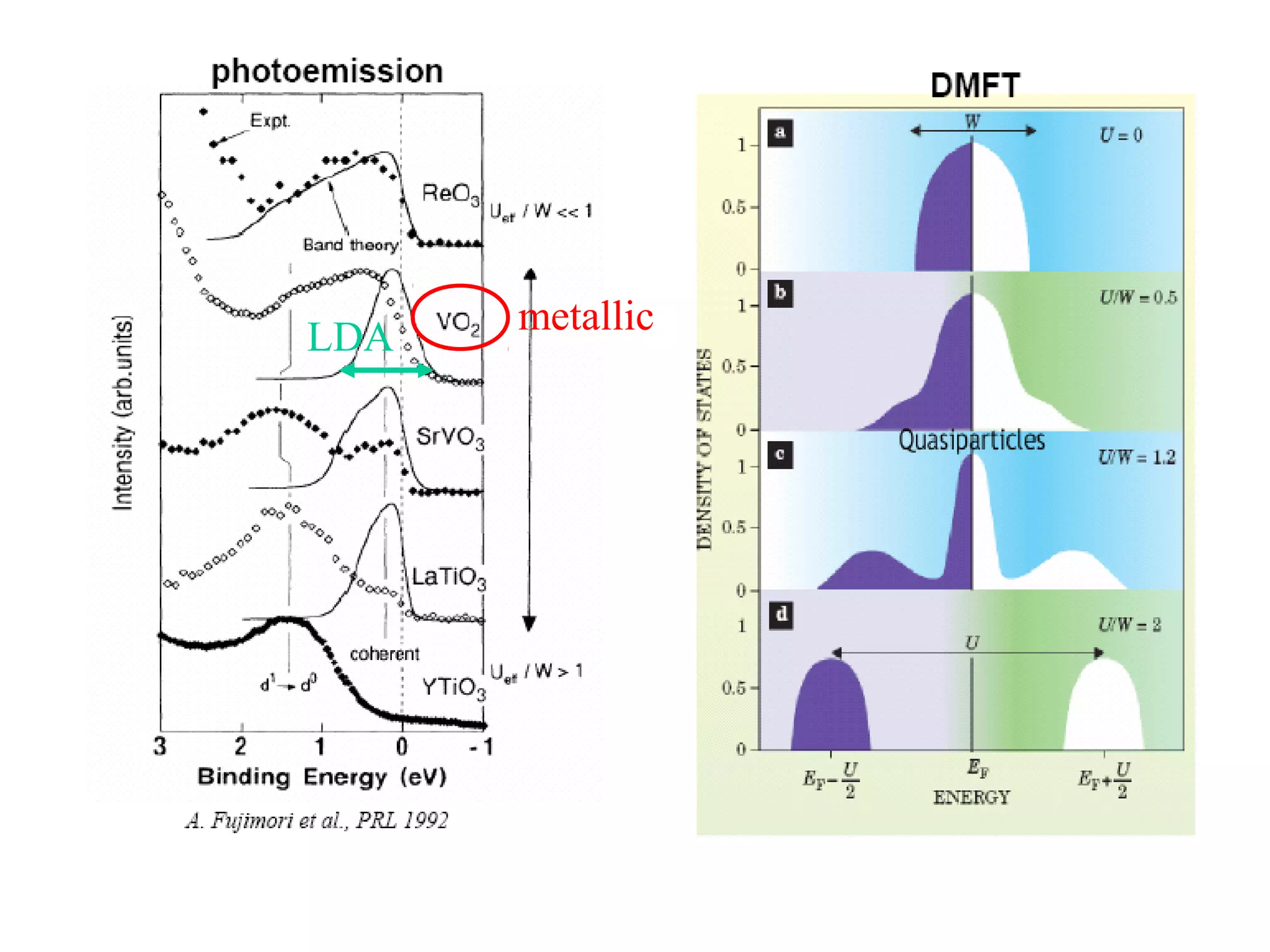
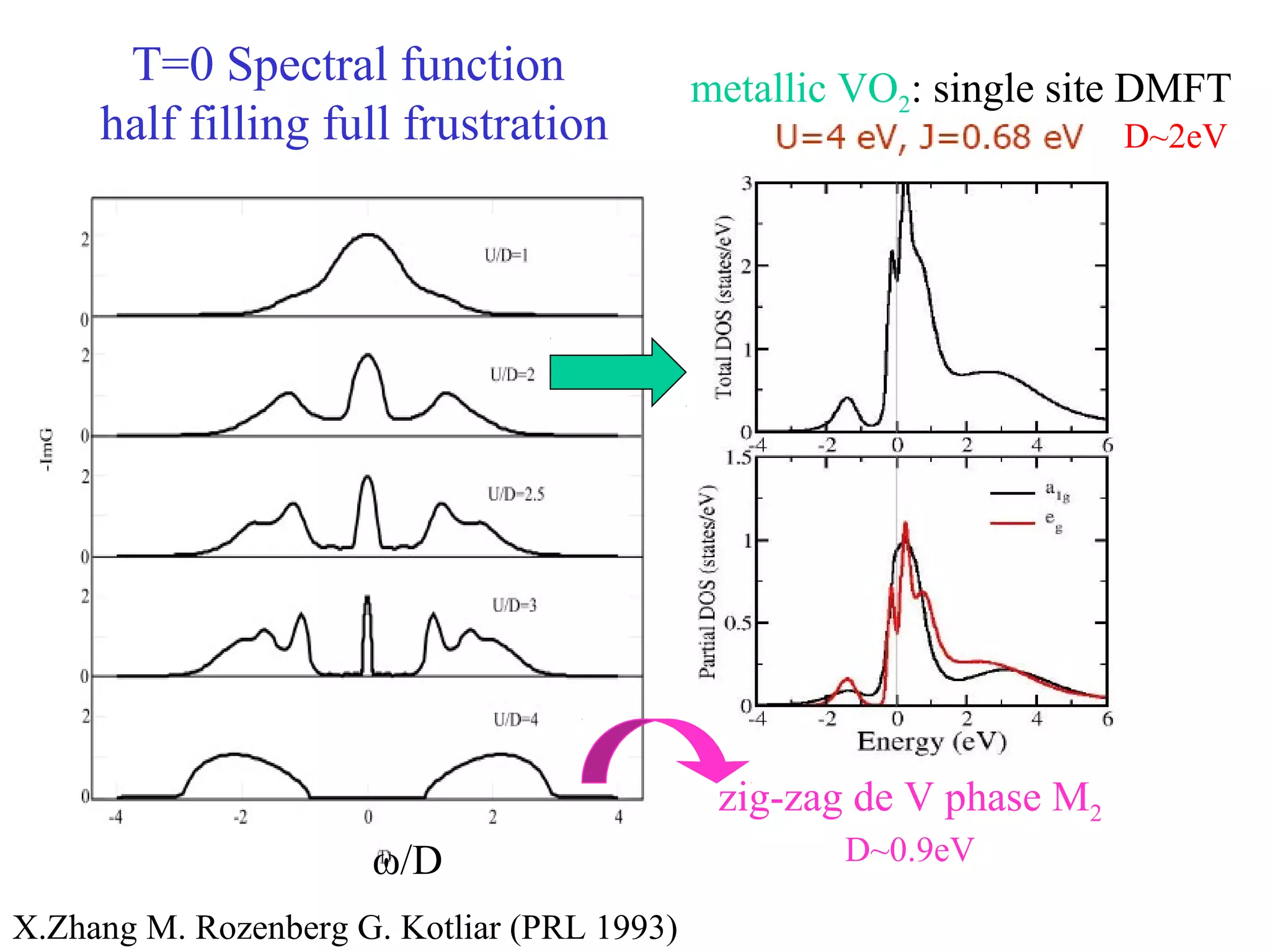
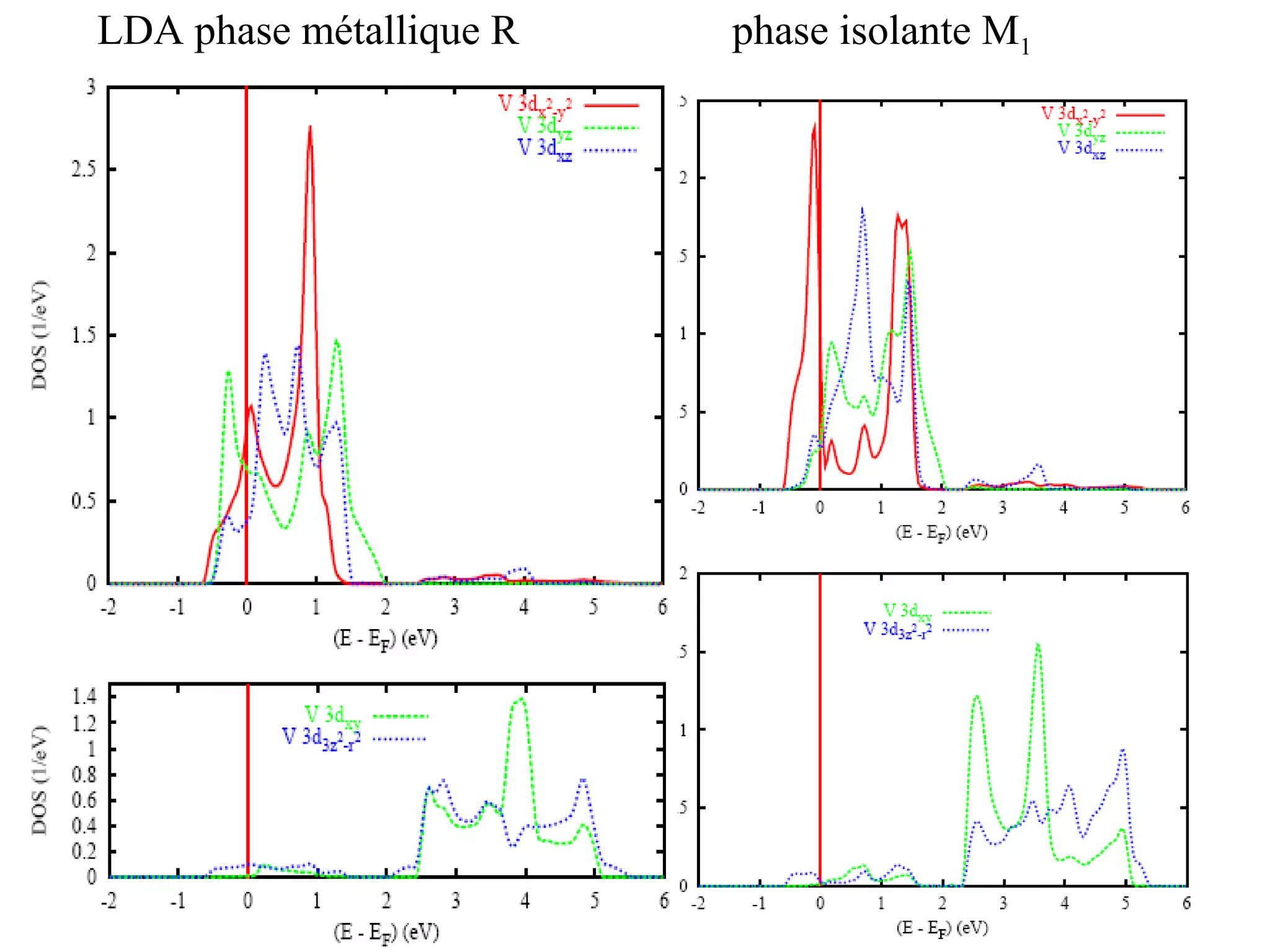
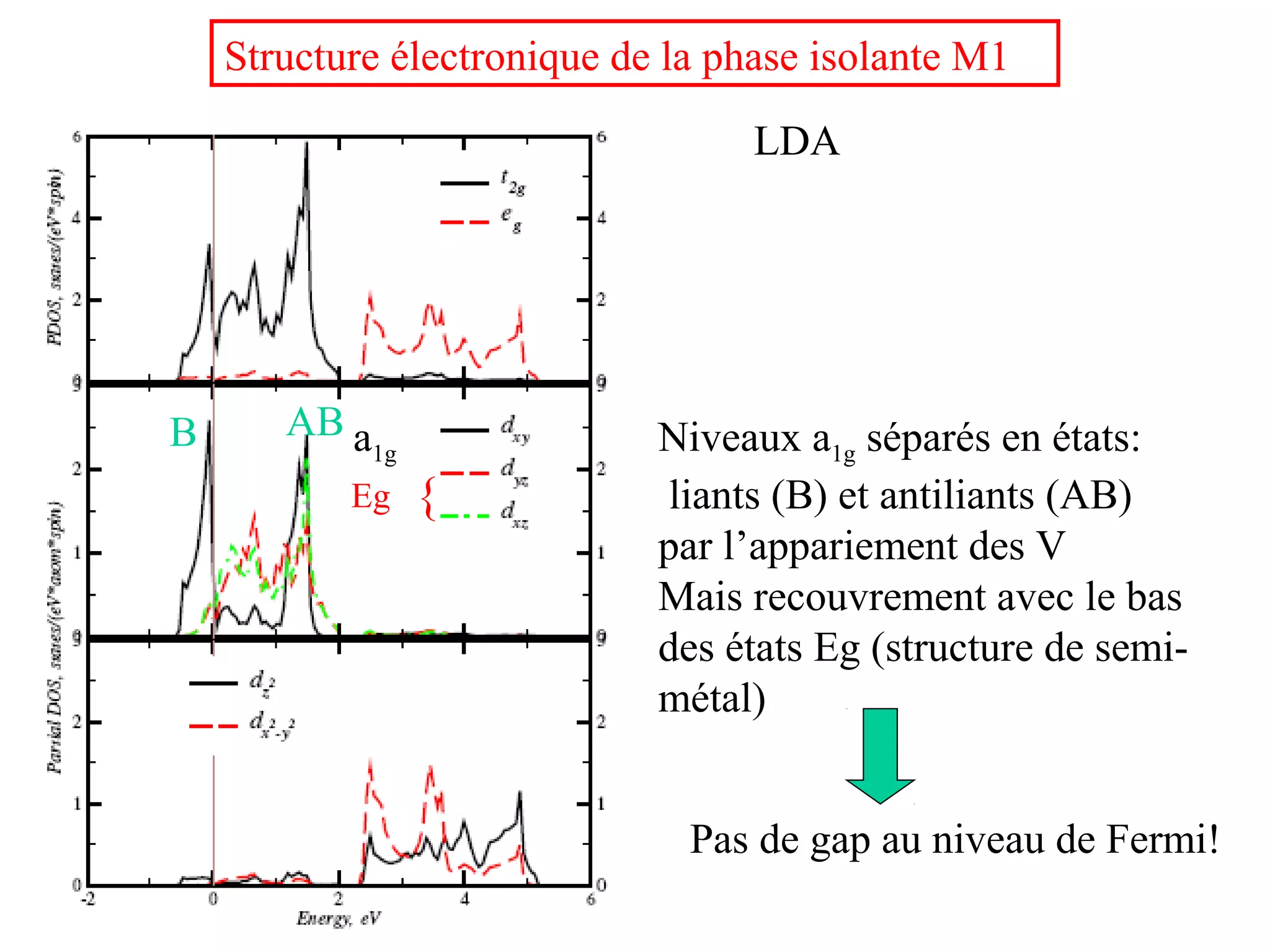
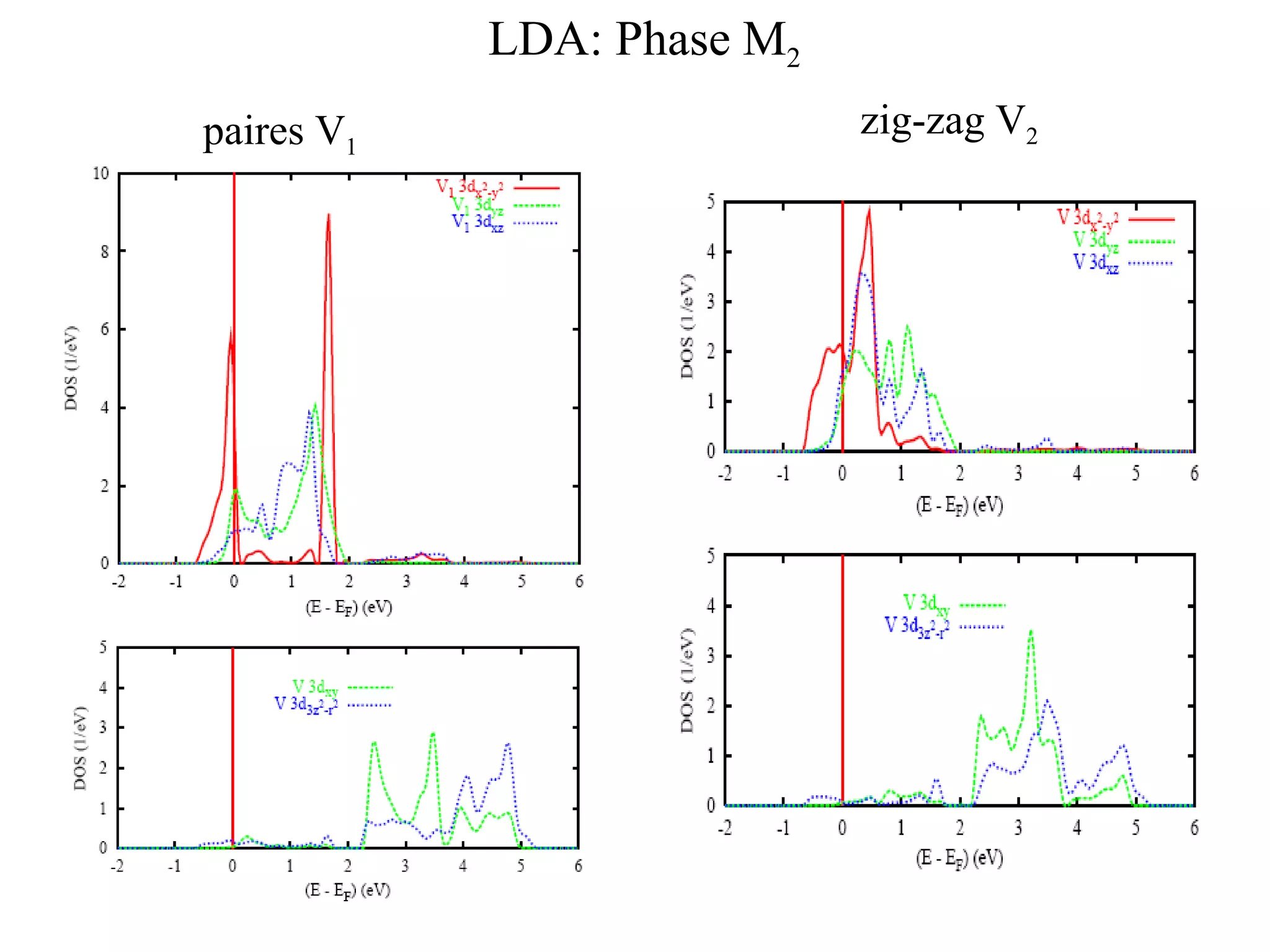
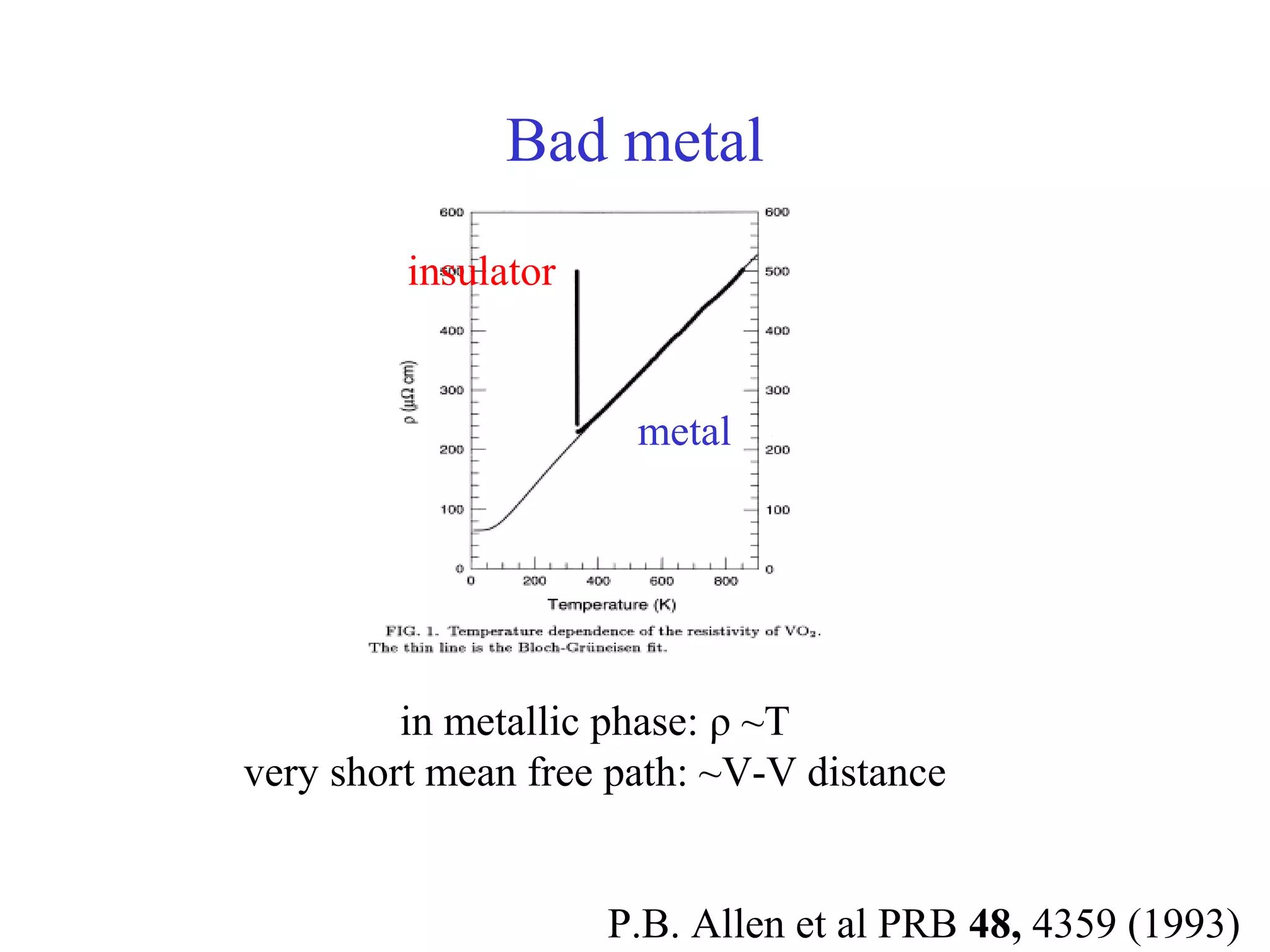
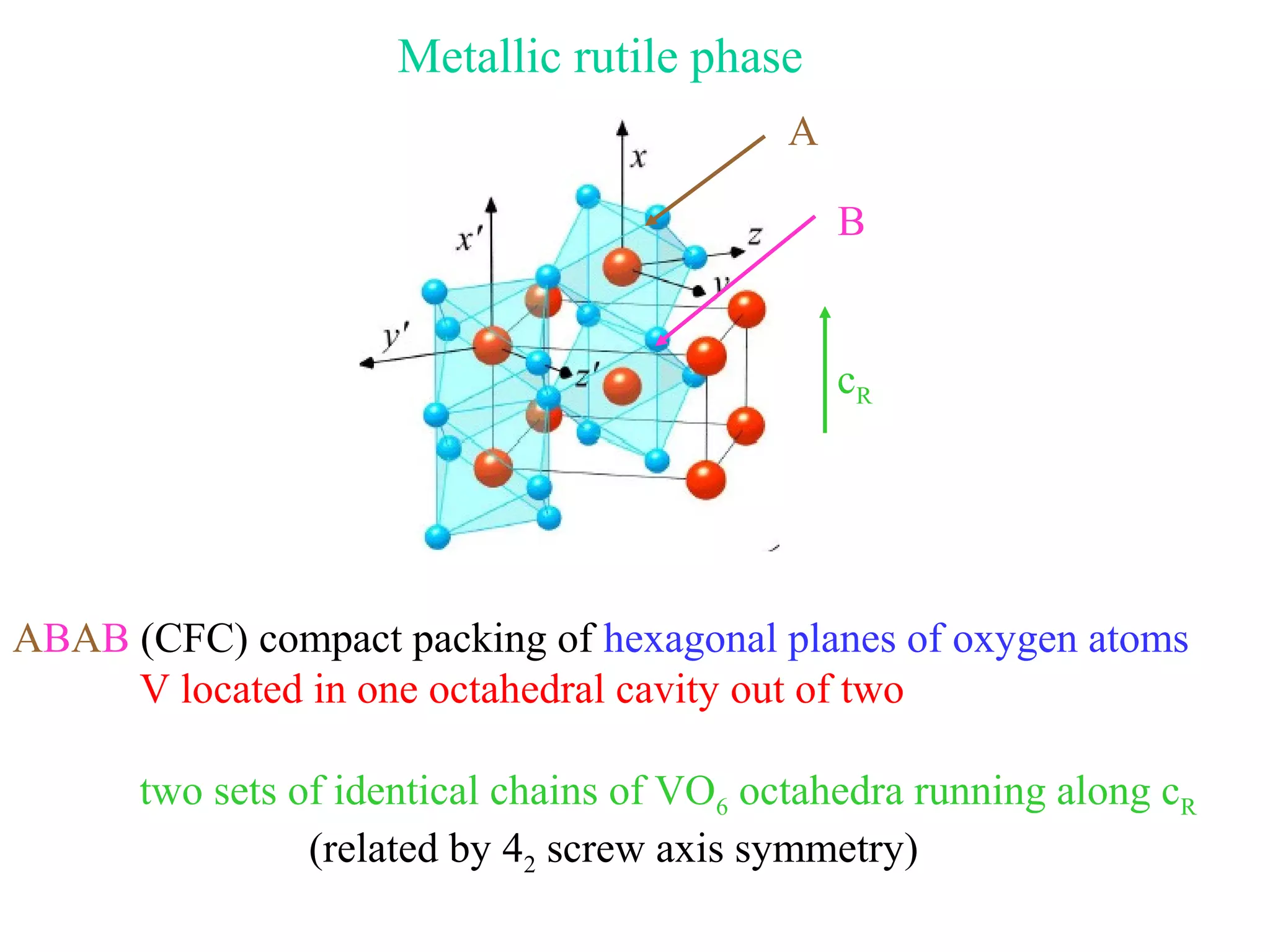
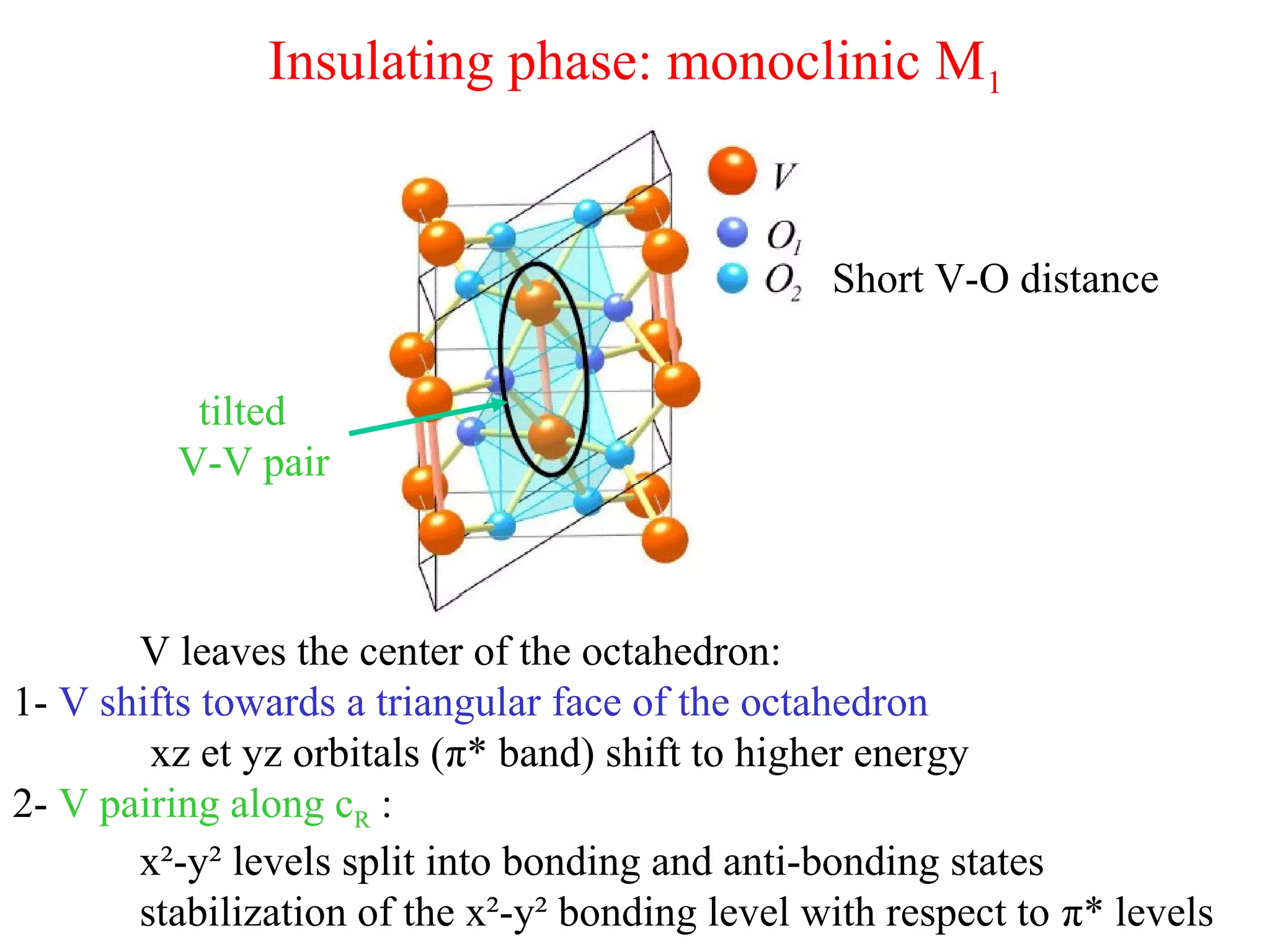
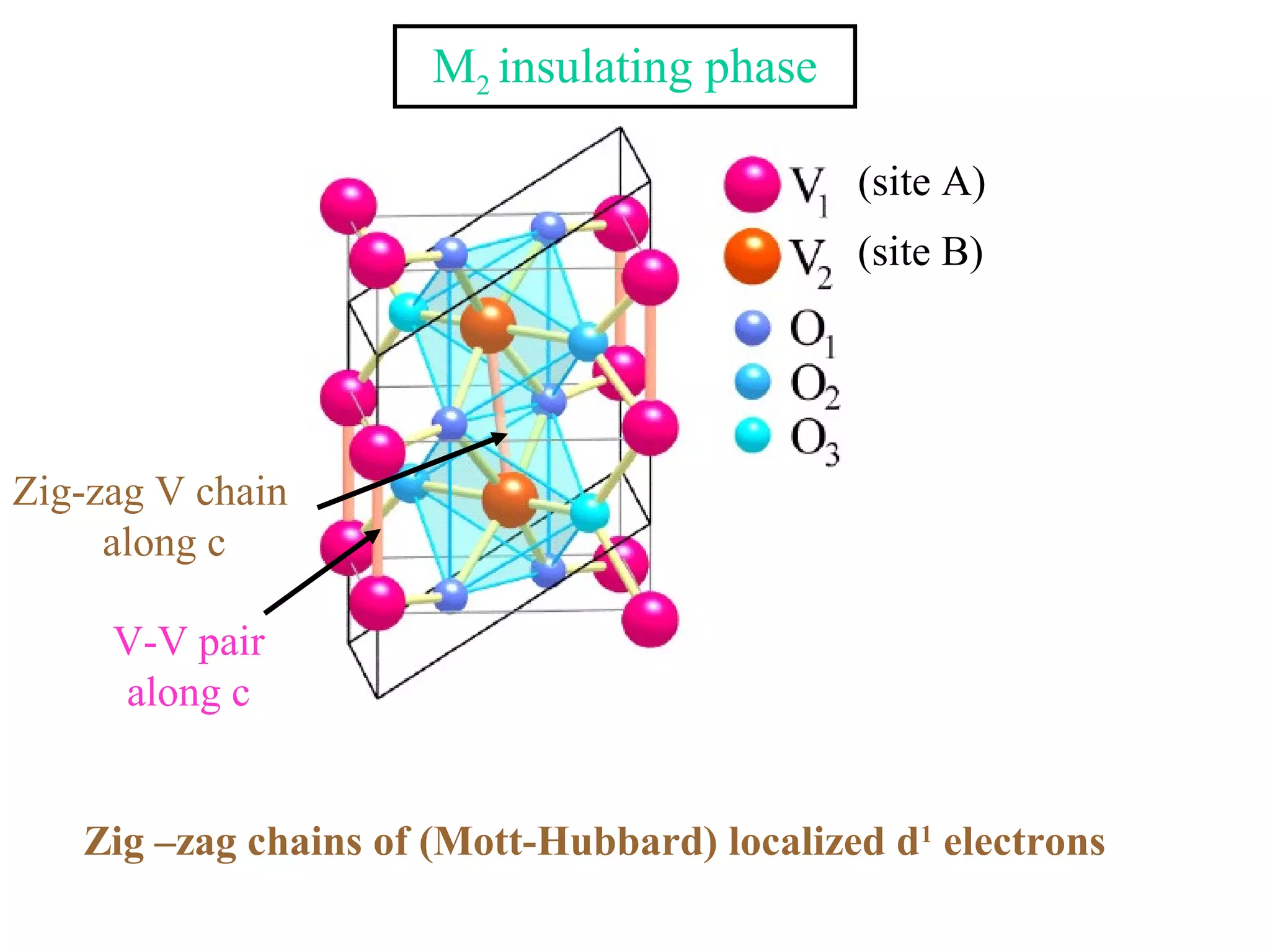
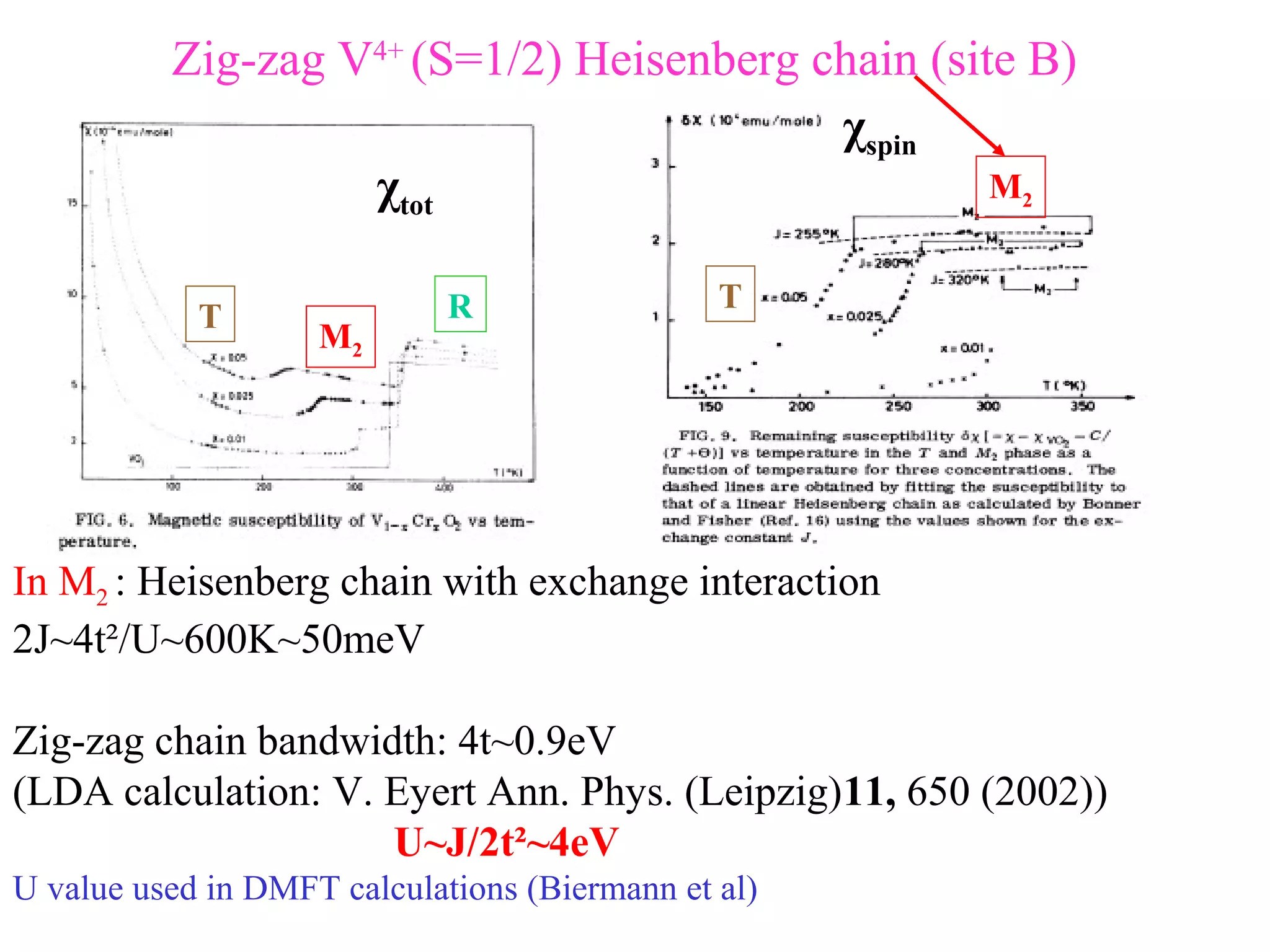
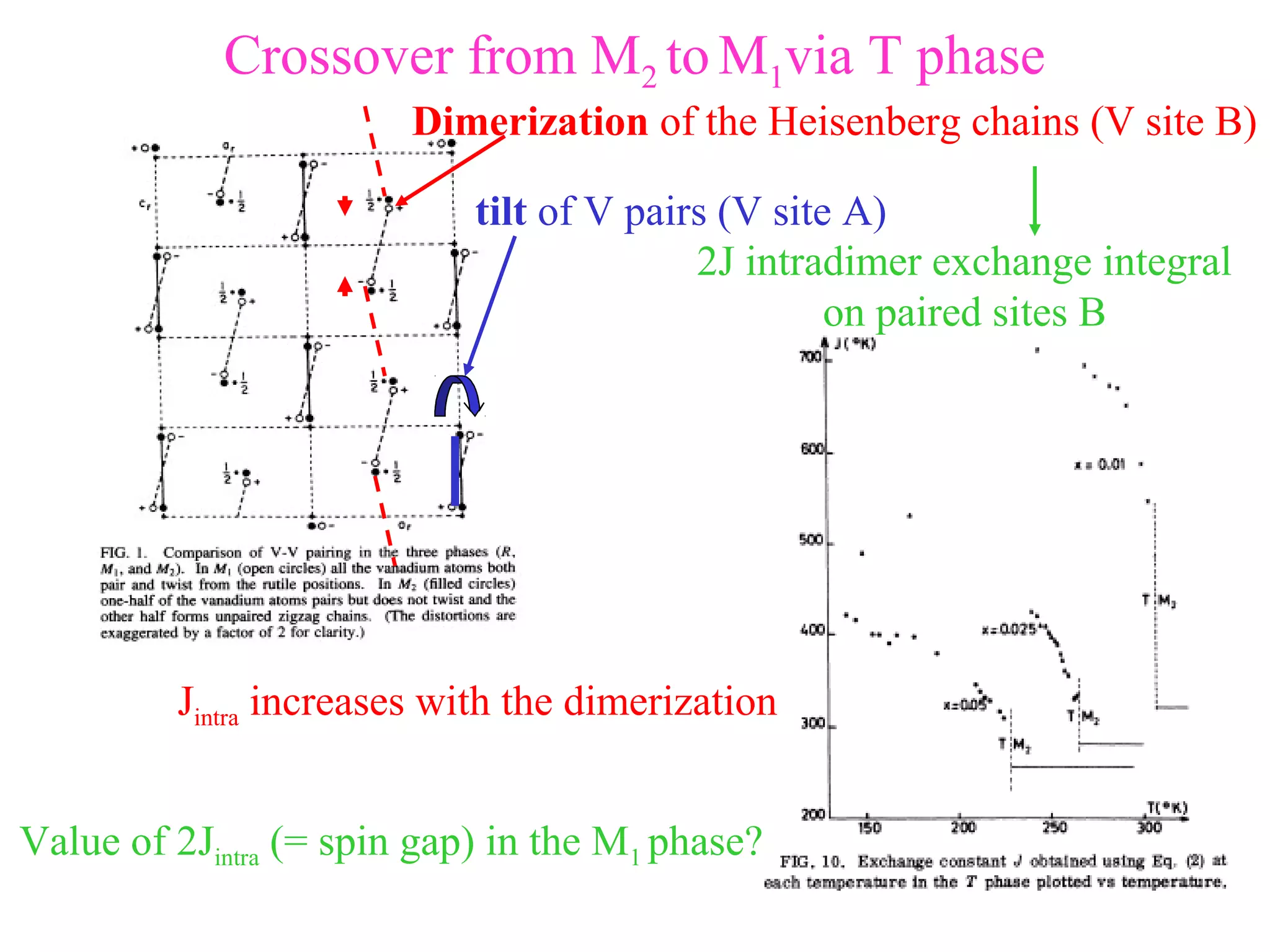
The document summarizes the metal-insulator transition in VO2, which occurs at 340K. In the metallic phase, VO2 exhibits bad metal behavior with short electron mean free paths. The insulating phase has two possible structures - M1 and M2. M1 involves pairing of V atoms and splitting of orbitals. M2 involves formation of zig-zag V chains. The transition may involve both Mott-Hubbard localization and a Peierls instability driven by soft phonon modes near the R point of the Brillouin zone. Precise values are estimated for the electronic parameters characterizing the insulating M1 phase, including Hubbard U, spin gap Δσ, and charge gap Δρ.

1. The metal-insulator transition of VO2
revisited
J.-P. Pouget
Laboratoire de Physique des Solides,
CNRS-UMR 8502,
Université Paris-sud 91405 Orsay
« Correlated electronic states in low dimensions »
Orsay 16 et 17 juin 2008
Conférence en l’honneur de Pascal Lederer

2. outline
• Electronic structure of metallic VO2
• Insulating ground states
• Role of the lattice in the metal-insulator
transition of VO2
• General phase diagram of VO2 and its
substituants

3. VO2: 1st
order metal-insulator transition at 340K
Discovered nearly 50 years ago
still the object of controversy!
*
*in fact the insulating ground state
of VO2 is non magnetic

4. Bad metal
in metallic phase: ρ ~T
very short mean free path: ~V-V distance
P.B. Allen et al PRB 48, 4359 (1993)
metal
insulator

5. Metallic rutile phase
cR
ABAB (CFC) compact packing of hexagonal planes of oxygen atoms
V located in one octahedral cavity out of two
two sets of identical chains of VO6 octahedra running along cR
(related by 42 screw axis symmetry)
A
B

6. eg:
t2g
V-O
σ* bonding
bonding between V in the (1,1,0) plane
(direct V-V bonding along cR :1D band?)
bonding between V in the (1,-1,0) plane in the (0,0,1) plane
V 3d orbitals in the xyz octahedral coordinate frame
V-O
π* bonding
orbital located in the
xy basis of the
octahedron
orbitals « perpendicular » to the
triangular faces of the octaedron

7. well splitted t2g and eg bands
V. Eyert Ann. Phys. (Leipzig)
11, 650 (2002)
3dyz and 3dxz: Eg or π* bands
of Goodenough
3dx²-y²: a1g or t// (1D) band of
Goodenough
Is it relevant to the physics of
metallic VO2?
LDA:
1d electron of the V4+
fills the 3 t2g bands
t2g
eg

8. Electronic structure of metallic VO2
LDA
Single site DMFT
Eg
a1g
t2g levels
bandwidth~2eV: weakly reduced in
DMFT calculations
U
LHB
UHB
Biermann et al PRL 94, 026404 (2005)
Hubbard bandson both Eg (π*)
and a1g (d//) states
no specificity of d// band!

9. Fractional occupancy of t2g orbitals
orbital/occupancy LDA* single site DMFT* EFG measurements**
x²-y² (d//) f1 0.36 0.42 0.41
yz (π*) f2 0.32 0.29 0.26-0.28
xz (π*) f3 0.32 0.29 0.33-0.31
*Biermann et al PRL 94, 026404 (2005)
** JPP thesis (1974): 51
V EFG measurements between 70°C and 320°C
assuming that only the on site d electron contributes to the EFG:
VXX = (2/7)e<r-3
> (1-3f2)
VYY = (2/7)e<r-3
> (1-3f3)
VZZ = (2/7)e<r-3
> (1-3f1)

10. VO2: a correlated metal?
• Total spin susceptiblity:
Neff (EF)~10 states /eV, spin direction
J.P. Pouget & H. Launois, Journal de Physique 37, C4-49 (1976)
• Density of state at EF:
N(EF)~1.3*, 1.5**, 2*** state/eV, spin direction
*LDA: Eyert Ann Phys. (Leipzig) 11, 650 (2002),
**LDA: Korotin et al cond-mat/0301347
***LDA and DMFT: Biermann et al PRL 94, 026404 (2005)
Enhancement factor of χPauli: 5-8

11. Sizeable charge fluctuations in the metallic state
• DMFT: quasiparticle band + lower (LHB) and
upper (UHB) Hubbard bands
• LHB observed in photoemission spectra
• VO2close to a Mott-Hubbard transition?
LHB
Koethe et al PRL 97, 116402 (2006)

12. Mott Hubbard transition for x increasing in
Nb substitued VO2: V1-XNbXO2?
• Nb isoelectronic of V but of larger size
• lattice parameters of the rutile phase strongly increase with x
• Very large increase of the spin susceptibility with x
NMR in the metallic state show that this increase is homogeneous (no local effects) for
x<xC
magnetism becomes more localized when x increases (Curis Weiss behavior of χspin for x
large)
• beyond xC ~0.2: electronic conductivity becomes activated
electronic charges become localized
local effects (induced by the disorder) become relevant near the metal-insulator transition
metal-insulator transition with x due to combined effect of correlations and
disorder
concept of strongly correlated Fermi glass (P. Lederer)

14. Insulating phase: monoclinic M1
tilted
V-V pair
V leaves the center of the octahedron:
1- V shifts towards a triangular face of the octahedron
xz et yz orbitals (π* band) shift to higher energy
2- V pairing along cR :
x²-y² levels split into bonding and anti-bonding states
stabilization of the x²-y² bonding level with respect to π* levels
Short V-O distance

15. Driving force of the metal-insulator
transition?
• The 1st
order metal- insulator transition induces a very large
electronic redistribution between the t2g orbitals
• Insulating non magnetic V-V paired M1ground state
stabilized by:
- a Peierls instability in the d// band ?
- Mott-Hubbard charge localization effects?
• To differentiate more clearly these two processes let us look
at alternative insulating phases stabilized in:
Cr substitued VO2
uniaxial stressedVO2
The x²-y² bonding level of the V4+
pair is occupied by 2 electrons of
opposite spin: magnetic singlet (S=0)

16. R-M1 transition of VO2 splitted into
R-M2-T-M1transitions
V1-XCrXO2
J.P. Pouget et al PRB 10,
1801 (1974)
VO2 stressed along [110]R
J.P. Pouget et al PRL 35,
873 (1975)

17. M2 insulating phase
Zig-zag V chain
along c
V-V pair
along c
(site B)
(site A)
Zig –zag chains of (Mott-Hubbard) localized d1
electrons

18. In M2 : Heisenberg chain with exchange interaction
2J~4t²/U~600K~50meV
Zig-zag chain bandwidth: 4t~0.9eV
(LDA calculation: V. Eyert Ann. Phys. (Leipzig)11, 650 (2002))
U~J/2t²~4eV
U value used in DMFT calculations (Biermann et al)
Zig-zag V4+
(S=1/2) Heisenberg chain (site B)
χtot
χspin
T
M2
R T
M2

19. Crossover from M2 to M1via T phase
tilt of V pairs (V site A)
Dimerization of the Heisenberg chains (V site B)
2J intradimer exchange integral
on paired sites B
Value of 2Jintra (= spin gap) in the M1 phase?
Jintra increases with the dimerization

20. Energy levels in the M1 phase
Δρ
Δρdimer
Δρdimer
Δσ
eigenstates of the 2 electrons
Hubbard molecule (dimer)
Only cluster DMFT is able to account for
the opening of a gap Δρat EF
(LDA and single site DMFT fail)
Δρdimer
~2.5-2.8eV >Δρ~0.6eV
(Koethe et al PRL 97,116402 (2006))
Δσ?
S
T
S
B
AB

21. Estimation of the spin gap Δσ in M1
• Shift of χbetween the T phase of V1-XAlXO2 and M1 phase of
VO2
• 51
V NMR line width broadening of site B in the T phase of
stressed VO2 :T1
-1
effect
for a singlet –triplet gap Δ: 1/T1~exp-Δ/kT
2J(M1)=Δσ >2100K
G. Villeneuve et al
J. Phys. C: Solid State
Phys. 10, 3621 (1977)
J.P. Pouget & H. Launois, Journal de Physique 37, C4-49 (1976)
M2
T

22. 50 60 70 80 90 100 110 120 130
200
400
600
800
1000
1200
Jintra(°K)
Vyy (KHz)
V1-X
CrX
O2
X=1%
stressed VO2
% T=295K
M1
T
M2
Jintra
B
(°K) + 270K ≈ 11.4 VYY
A
(KHz)
The intradimer exchange integral Jintra of the dimerized Heisenberg chain
(site B) is a linear function of the lattice deformation measured by the 51
V
component VYY on site A
For VYY= 125KHz (corresponding to V pairing in the M1 phase) one
gets : Jintra~1150K or Δσ~2300K
Site B
Site A

23. M1 ground state
Δσ~ 0.2eV<<Δρ is thus caracteristic of an electronic
state where strong coulomb repulsions lead to a spin
charge separation
The M1 ground state thus differs from a conventional
Peierls ground state in a band structure of non
interacting electrons where the lattice instability
opens equal charge and spin gaps Δρ ~ Δσ

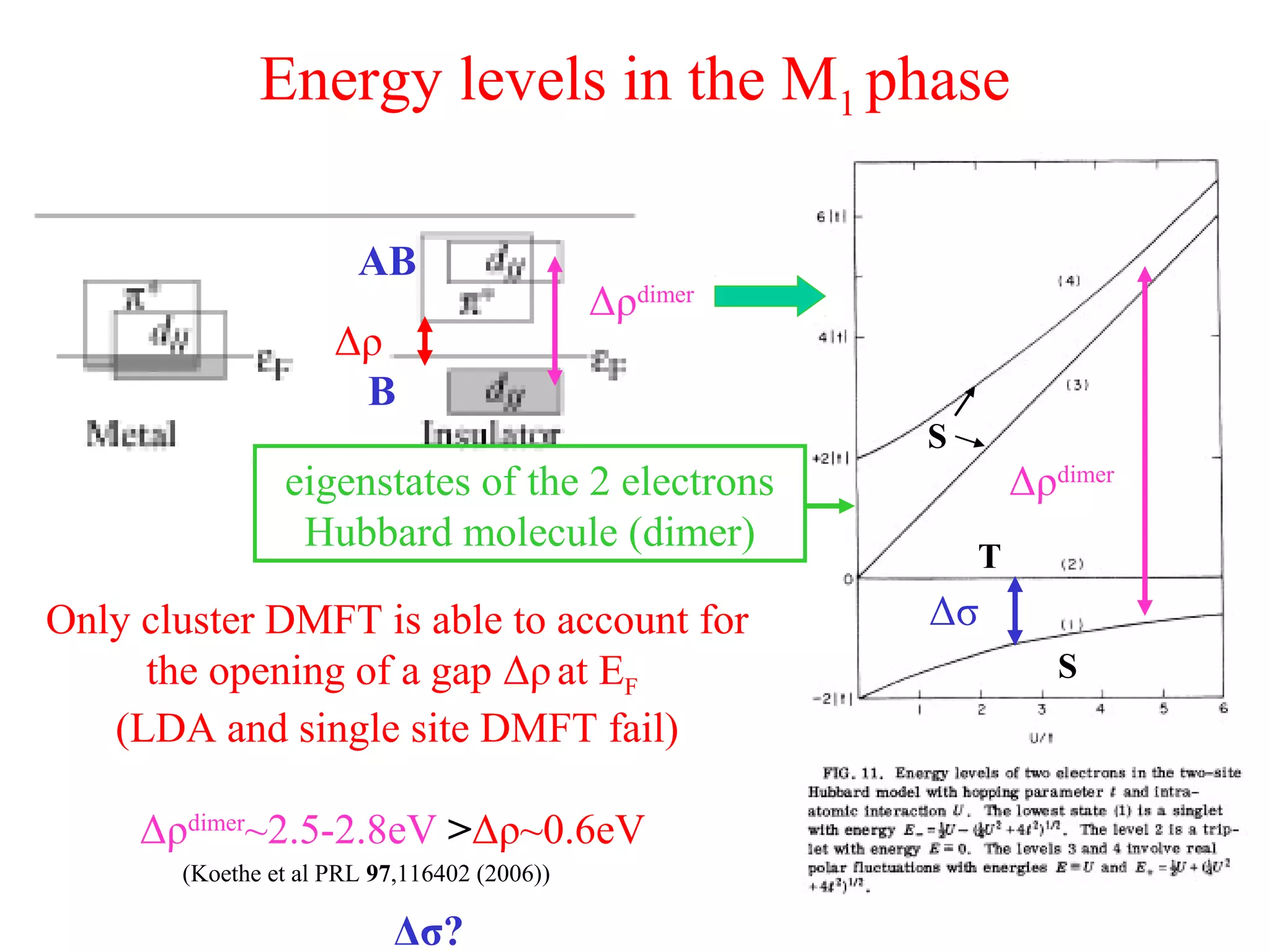
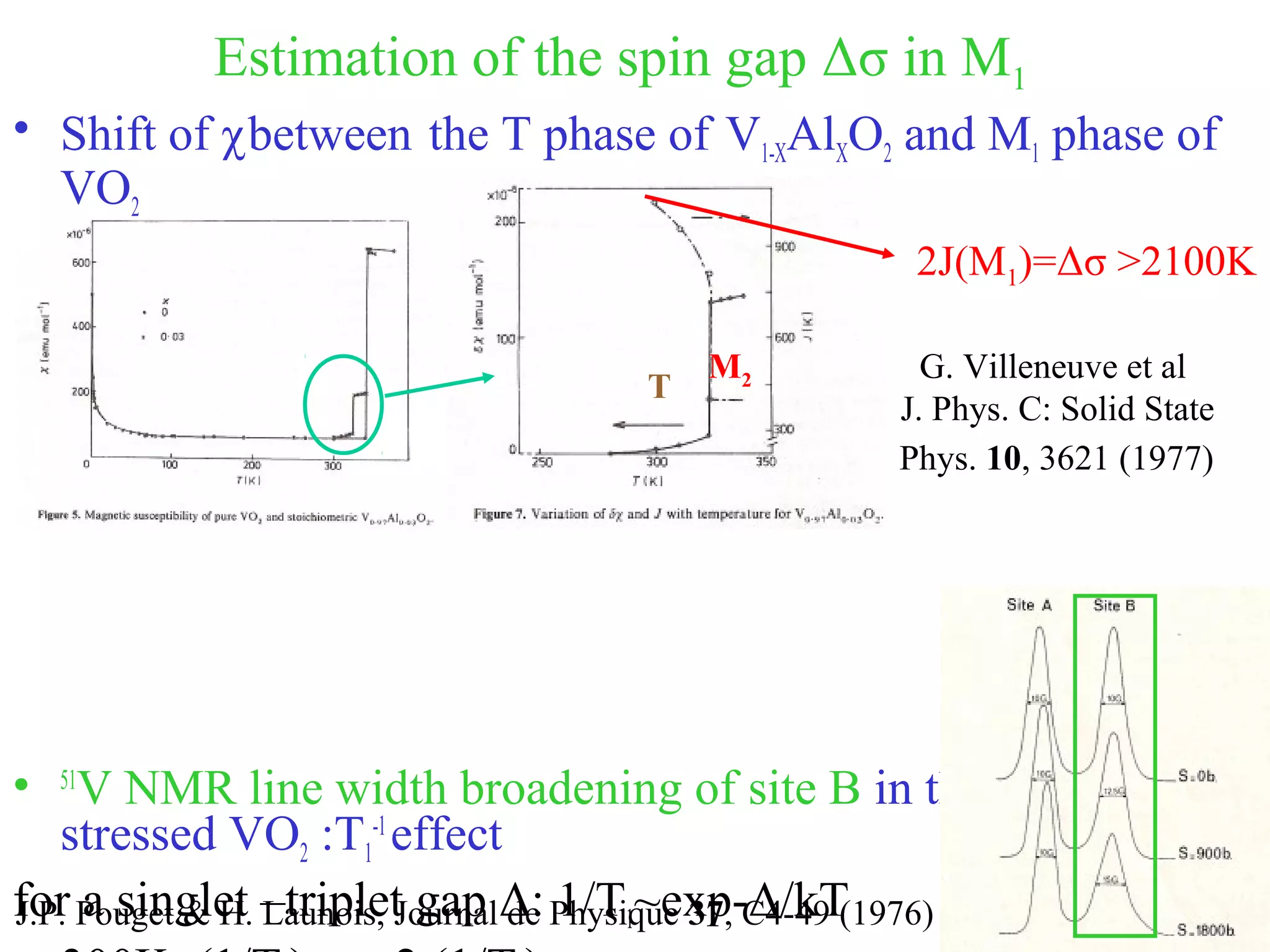
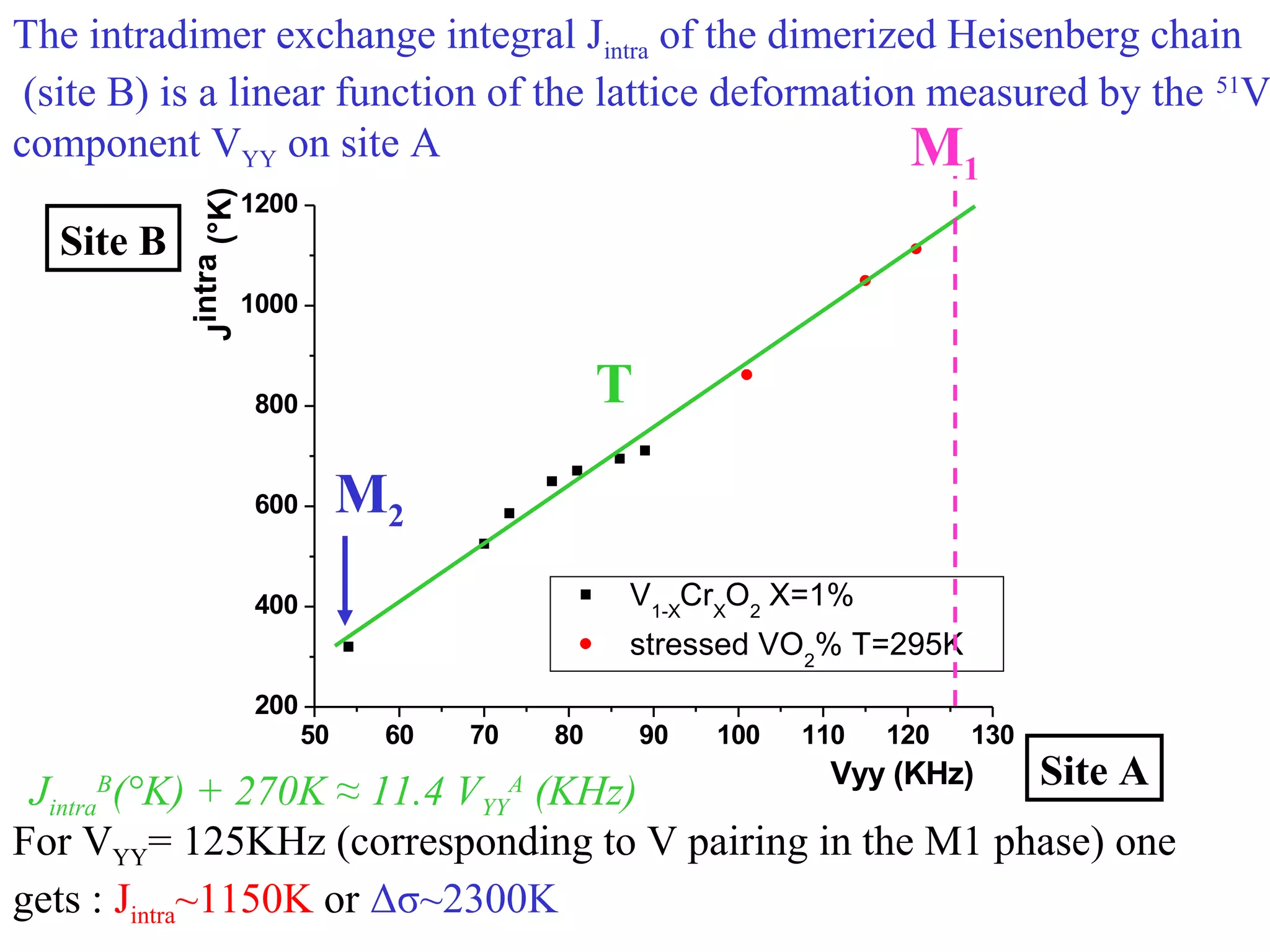
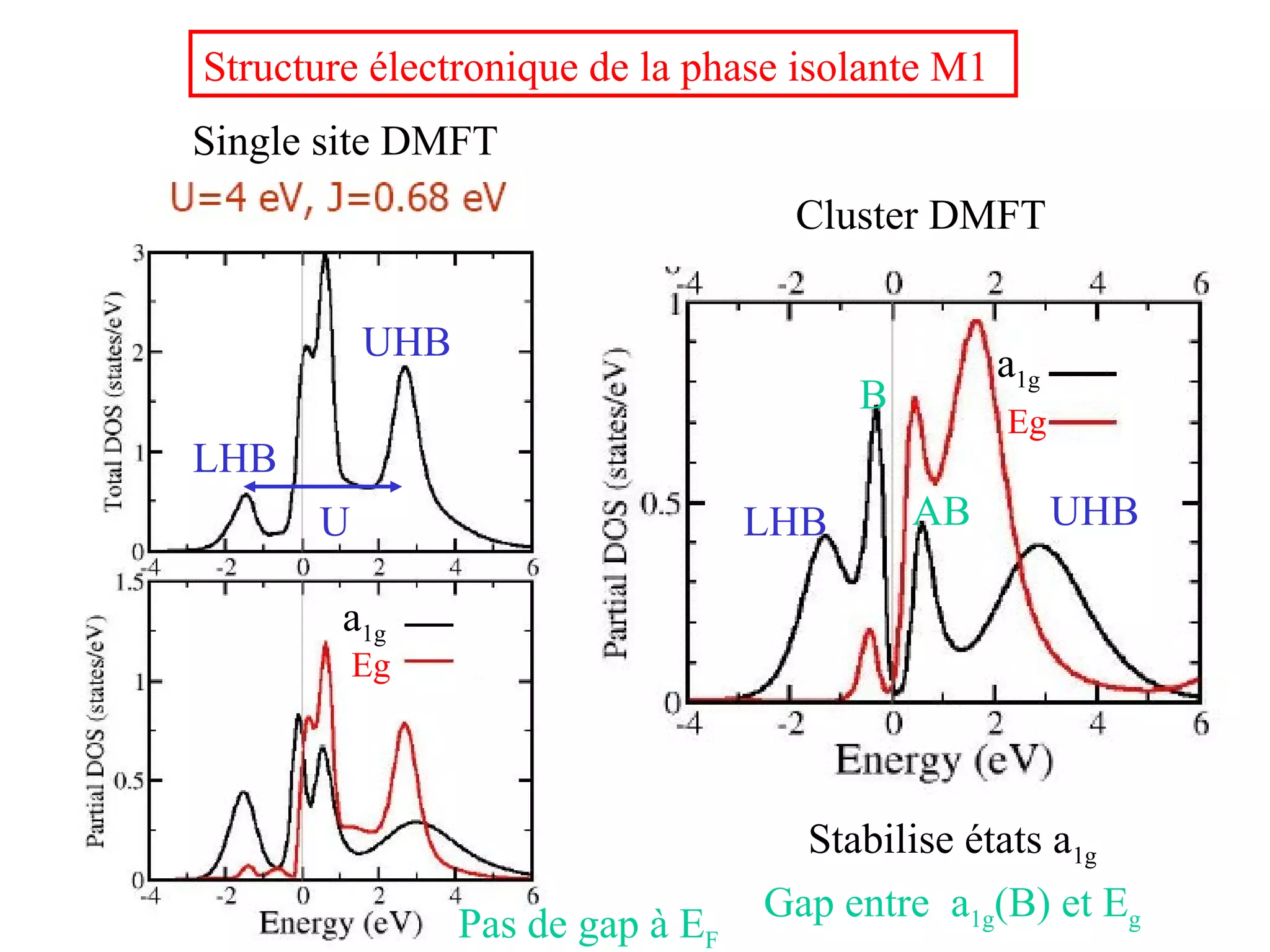
24. Electronic parameters of the M1 Hubbarddimer
• Spin gap value Δσ ~ 0.2 eV
Δσ= [-U+ (U²+16t²)1/2
]/2
which leads to:
2t ≈ (Δσ Δρintra
)1/2
≈0.7eV
2t amounts to the splitting between bonding and anti-bonding quasiparticle states
in DMFT (0.7eV) and cluster DMFT (0.9eV) calculations
2t is nearly twice smaller than the B-AB splitting found in LDA (~1.4eV)
• U ≈ Δρintra
-Δσ ~ 2.5eV
(in the M2 phase U estimated at ~4eV)
• For U/t ~ 7
double site occupation ~ 6% per dimer
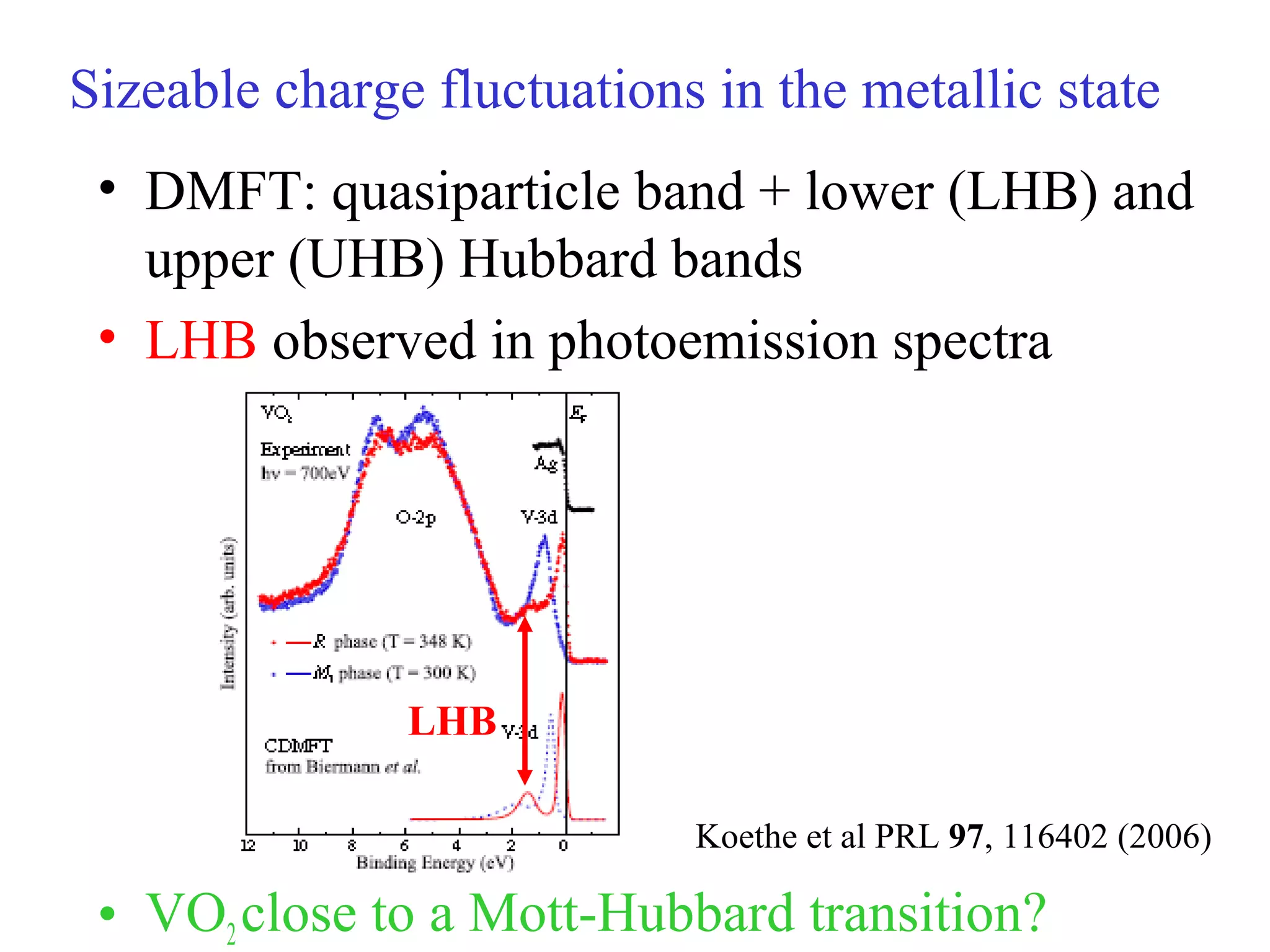
nearly no charge fluctuations no LHB seen in photoemission
ground state wave function very close to the Heitler-London limit*
*wave function expected for a spin-Peierls ground state
The ground state of VO2 is such that Δσ~7J (strong coupling limit)
In weak coupling spin-Peierls systems Δσ<J

25. Lattice effects
• the R to M1 transformation (as well as R to M2 or T transformations) involves:
- the critical wave vectors qc of the « R » point star:{(1/2,0,1/2) , (0,1/2,1/2)}
- together, with a 2 components (η1,η2) irreductible representation for each qC:
ηi corresponds to the lattice deformation of the M2phase:
formation of zig-zag V chain (site B) + V-V pairs (site A)
the zig-zag displacements located are in the (1,1,0)R/ (1,-1,0)R planes for i=1 / 2
M2: η1≠0, η2= 0 T: η1> η2≠0 M1: η1= η2≠0
• The metal-insulator transition of VO2 corresponds to a lattice instability at a
single R point
Is it a Peierls instability with formation of a charge density wave driven by the
divergence of the electron-hole response function at a qc which leads to good
nesting properties of the Fermi surface?
• Does the lattice dynamics exhibits a soft mode whose critical wave vector qc is
connected to the band filling of VO2?
• Or is there an incipient lattice instability of the rutile structure used to trig the
metal-insulator transition?

26. Evidences of soft lattice dynamics
• X-ray diffuse scattering experiments show the presence of {1,1,1}
planes of « soft phonons » in rutile phase of
(metallic)VO2 (insulating) TiO2
(R. Comès, P. Felix and JPP: 35 years old unpublished results)
aR*/2
aR*/2
cR*/2
R critical point of VO2
P critical point of NbO2
Γ critical point of TiO2
(incipient ferroelectricity
of symmetry A2U and
2x degenerate EU)
+(001) planes
{u//cR}
[001]
[110]
A2U
EU
{u//[110]}
smeared diffuse
scattering ┴ c*R

27. {1,1,1} planar soft phonon modes in VO2
• not related to the band filling (the diffuse scattering exists also in TiO2)
• 2kFof the d//band does not appear to be a pertinent critical wave vector
as expected for a Peierls transition
but the incipient (001)-like diffuse lines could be the fingerprint of a 4kFinstability
(not critical) of fully occupied d// levels
• instability of VO2 is triggerred by an incipient lattice instability of the
rutile structure which tends to induce a V zig-zag shift*
ferroelectric V shift along the [110] / [1-10] direction* (degenerate RI?) accounts for the
polarisation of the diffuse scattering
correlated V shifts along [111] direction give rise to the observed (111) X-ray diffuse
scattering sheets
*the zig-zag displacement destabilizes the π* orbitals
a further stabilization of d// orbitals occurs via the formation of bonding levels
achieved by V pairing between neighbouring [111] « chains »
[111]
[110
]cR
[1-
10]

28. phase diagram of substitued VO2
R
M1
0.03x
V1-XMXO2
0
dTMI/dx ≈ -12K/%V3+
uniaxial stress // [110]R
xV5+
V3+
M=Cr, Al,Fe
VO2+y
VO2-yFy
M=Nb, Mo, W
Oxydation of V4+
Reduction of V4+
MVO2
dTMI/dx≈0
Sublatices A≡B Sublatices A≠B

29. Main features of the general phase diagram
• Substituants reducing V4+
in V3+
: destabilize
insulating M1* with respect to metallic R
formation of V3+
costs U: the energy gain in the
formation of V4+
-V4+
Heitler-London pairs is lost
dTMI/dx ≈ -1200K per V4+
-V4+
pair broken
Assuming that the energy gain ΔU is a BCS like condensation energy
of a spin-Peierls ground state:
ΔU=N(EF)Δσ²/2
One gets: ΔU≈1000K per V4+
- V4+
pair (i.e. per V2O4formula unitof M1)
with Δσ~0.2eV and N(EF)=2x2states per eV, spin direction and V2O4 f.u.
*For large x, the M1 long range order is destroyed, but the local V-V pairing remains

30. Main features of the general phase diagram
• Substituants reducing V4+
in V5+
: destabilize insulating M1
with respect to new insulating T and M2phases
butleaves unchangedmetal-insulator transition: dTMI/dx≈0
below R: the totally paired M1phase is replaced by the half
paired M2 phase
formation of V5+
looses also thepairing energy gain but does not kill
the zig-zag instability (also present in TiO2!)
as a consequence the M2phase is favored
uniaxial stress along [110] induces zig-zag V displacements along [1-10]
Note the non symmetric phase diagram with respect to
electron and hole « doping » of VO2!

31. Comparison of VO2 and BaVS3
• Both are d1
V systems where the t2gorbitals are partly filled
(but there is a stronger V-X hybridation for X=S than for X=O)
• BaVS3undergoes at 70K a 2nd
order Peierls M-I transition driven by a 2kF CDW
instability in the 1D d// band responsible of the conducting properties
at TMI tetramerization of V chains without charge redistribution among the t2g’s
(Fagot et al PRL90,196403 (2003))
• VO2undergoes at 340K a 1st
order M-I transition accompanied by a large charge
redistribution among the t2g’s
Structuralinstability towards the formation of zig-zag V shifts in metallic VO2
destabilizes the π* levels and thus induces a charge redistribution in favor of the d//
levels
The pairing (dimerization) provides a further gain of energy by putting the d//
levels into a singlet bonding state*
*M1 phase exhibits a spin-Peierls like ground state
This mechanism differs of the Peierls-like V pairing scenario proposed by
Goodenough!

32. acknowledgements
• During the thesis work
H. Launois
P. Lederer
T.M. Rice
R. Comès
J. Friedel
• Renew of interest from recent DMFT calculations
A. Georges
S. Biermann
A. Poteryaev
J.M. Tomczak

33. Supplementary material

34. Main messages
• Electron-electron interactions are important in VO2
- in metallic VO2: important charge fluctuations (Hubbard bands)
Mott-Hubbard like localization occurs when the lattice expands
(Nb substitution)
- in insulating VO2: spin-charge decoupling
ground state described by Heitler-London wave function
• The 1ST
order metal-insulator transitionis accompanied by a large
redistribution of charge between d orbitals.
for achieving this proccess an incipient lattice instability of the rutile
structure is used.
It stabilizes a spin-Peierls like ground state with V4+
(S=1/2) pairing
• The asymmetric features of the general phase diagram of substitued
VO2 must be more clearly explained!

35. LDA
metallic

36. T=0 Spectral function
half filling full frustration
X.Zhang M. Rozenberg G. Kotliar (PRL 1993)
ω/D
metallic VO2: single site DMFT
D~2eV
zig-zag de V phase M2
D~0.9eV

37. LDA phase métallique R phase isolante M1

38. Structure électronique de la phase isolante M1
LDA LDA
Pas de gap au niveau de Fermi!
Eg {
a1g
B AB Niveaux a1g séparés en états:
liants (B) et antiliants (AB)
par l’appariement des V
Mais recouvrement avec le bas
des états Eg (structure de semi-
métal)

39. Cluster DMFT
Gap entre a1g(B) et Eg
Structure électronique de la phase isolante M1
Eg
a1g
Single site DMFT
Pas de gap à EF
Eg
a1g
LHB
UHB
U
B
ABLHB UHB
Stabilise états a1g

40. LDA: Phase M2
paires V1
zig-zag V2