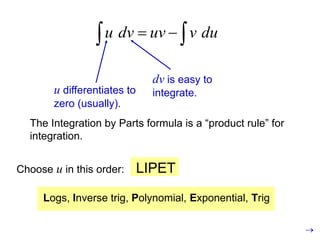
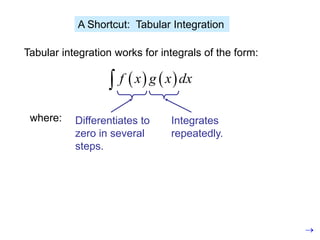
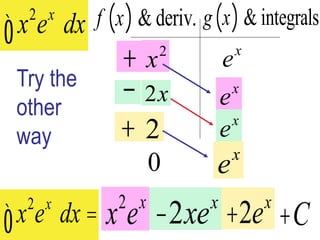
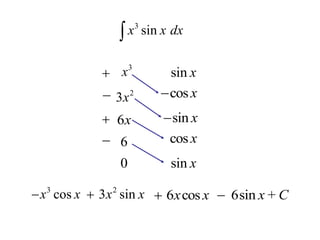This document provides an overview of integration techniques in calculus, including integration by parts, trigonometric integrals, and tabular integration. Integration by parts uses the product rule to find antiderivatives of functions that are products, allowing one to integrate more complicated functions. Tabular integration provides a shortcut method for integrals where one factor differentiates to zero and the other integrates repeatedly. Examples are provided to demonstrate how to use these techniques to evaluate definite integrals.

2. ‫والتكامل‬ ‫التفاضل‬ ‫حساب‬
Differential and Integral Calculus
‫اعداد‬
‫أ‬
.
‫م‬
.
‫د‬
/
‫محمد‬ ‫مدحت‬ ‫تامر‬
‫والنظم‬ ‫الحاسبات‬ ‫هندسة‬ ‫مساعد‬ ‫أستاذ‬
‫الهندسة‬ ‫كلية‬
–
‫كفرالشيخ‬ ‫جامعة‬
‫والطالب‬ ‫التعليم‬ ‫لشئون‬ ‫االصطناعي‬ ‫الذكاء‬ ‫كلية‬ ‫وكيل‬
tmedhatm@eng.kfs.edu.eg
www.kfs.edu.eg/drtamer.html
Kafrelsheikh University
‫يخ‬ ‫شــــ‬ ‫ال‬ ‫ـفر‬ ‫ك‬ ‫عة‬ ‫ـ‬ ‫جام‬
Kafrelsheikh University
‫يخ‬ ‫شــــ‬ ‫ال‬ ‫ـفر‬ ‫ك‬ ‫عة‬ ‫ـ‬ ‫جام‬
Kafrelsheikh University
‫يخ‬ ‫شــــ‬ ‫ال‬ ‫ـفر‬ ‫ك‬ ‫عة‬ ‫ـ‬ ‫جام‬

3. .
‫ر‬‫للمقر‬‫والتقييم‬‫التدريس‬‫ق‬‫طر‬
‫المقرر‬ ‫اسم‬
‫الفصل‬
‫الثانى‬
‫األسبوعية‬ ‫الساعات‬
‫الدرجات‬
‫مدة‬
‫االمتحان‬
‫محاضرة‬
‫تمرين‬
‫تحريري‬
‫سنة‬ ‫أعمال‬
‫عملي‬
‫التفاضل‬ ‫حساب‬
‫والتكامل‬
2
2
60
20
20
2

4. MATH221: Differential and Integral
Calculus
Techniques of integration:
• Integration by parts, trigonometric integrals and
substitutions, integrals of rational functions,
quadratic expressions, tables of integrals, improper
integrals.
Differential equations:
• Definition, classifications and terminology,
techniques of solution of ordinary first-order first-
degree differential equations (separable, reducible
to separable, homogeneous, reducible to
homogeneous, linear, reducible to linear, exact
differential, nonexact differential-integrating factor),

5. TECHNIQUES OF
INTEGRATION
• Due to the Fundamental Theorem of
Calculus (FTC), we can integrate a
function if we know an antiderivative,
that is, an indefinite integral.
– We summarize the most important integrals
we have learned so far, as follows.

6. FORMULAS OF INTEGRALS
1
1
( 1) ln | |
1
ln
n
n
x
x x x
x
x dx C n dx x C
n x
a
e dx e C a dx C
a

     

   
 
 

7. 2 2
sin cos cos sin
sec tan csc cot
sec tan sec csc cot csc
x dx x C x dx x C
dx x C dx x C
x x dx x C x x dx x C
    
    
    
 
 
 
FORMULAS OF INTEGRALS

8. 1 1
2 2 2 2
sinh cosh cosh sinh
tan ln |sec | cot ln |sin |
1 1 1
tan sin
xdx x C xdx x C
xdx x C xdx x C
x x
dx C dx C
x a a a a
a x
 
   
   
   
   
   
    

 
 
 
FORMULAS OF INTEGRALS

9. TECHNIQUES OF INTEGRATION
• In this chapter, we develop techniques
for using the basic integration formulas.
– This helps obtain indefinite integrals of
more complicated functions.

10. Integration By Parts
Start with the product rule:
 
d dv du
uv u v
dx dx dx
 
 
d uv u dv v du
 
 
d uv v du u dv
 
 
u dv d uv v du
 
 
 
u dv d uv v du
 
 
 
 
u dv d uv v du
 
  
u dv uv v du
 
 
This is the Integration by Parts
formula.


11. u dv uv v du
 
 
The Integration by Parts formula is a “product rule” for
integration.
u differentiates to
zero (usually).
dv is easy to
integrate.
Choose u in this order: LIPET
Logs, Inverse trig, Polynomial, Exponential, Trig


12. Example 1:
cos
x x dx


polynomial factor u x

du dx

cos
dv x dx

sin
v x

u dv uv v du
 
 
LIPET
sin cos
x x x C
  
u v v du
 
sin sin
x x x dx
  


13. Example:
ln x dx

logarithmic factor ln
u x

1
du dx
x

dv dx

v x

u dv uv v du
 
 
LIPET
ln
x x x C
 
1
ln x x x dx
x
  

u v v du
 


14. This is still a product, so we
need to use integration by
parts again.
Example 4:
2 x
x e dx

u dv uv v du
 
  LIPET
2
u x
 x
dv e dx

2
du x dx
 x
v e

u v v du
 
2
2
x x
x e e x dx
 

2
2
x x
x e xe dx
  u x
 x
dv e dx

du dx
 x
v e

 
2
2
x x x
x e xe e dx
  
2
2 2
x x x
x e xe e C
  


15. Example 5:
cos
x
e x dx

LIPET
x
u e
 sin
dv x dx

x
du e dx
 cos
v x
 
u v v du
 
sin sin
x x
e x x e dx
 

 
sin cos cos
x x x
e x e x x e dx
    

x
u e
 cos
dv x dx

x
du e dx
 sin
v x

sin cos cos
x x x
e x e x e x dx
  
This is the
expression we
started with!

uv v du

16. Example 6:
cos
x
e x dx

LIPET
u v v du
 
cos
x
e x dx 

2 cos sin cos
x x x
e x dx e x e x
 

sin cos
cos
2
x x
x e x e x
e x dx C

 

sin sin
x x
e x x e dx
 

x
u e
 sin
dv x dx

x
du e dx
 cos
v x
 
x
u e
 cos
dv x dx

x
du e dx
 sin
v x

sin cos cos
x x x
e x e x e x dx
  
 
sin cos cos
x x x
e x e x x e dx
    


17. Example 6:
cos
x
e x dx

u v v du
 
This is called “solving
for the unknown
integral.”
It works when both
factors integrate and
differentiate forever.

cos
x
e x dx 

2 cos sin cos
x x x
e x dx e x e x
 

sin cos
cos
2
x x
x e x e x
e x dx C

 

sin sin
x x
e x x e dx
 

sin cos cos
x x x
e x e x e x dx
  
 
sin cos cos
x x x
e x e x x e dx
    


18. A Shortcut: Tabular Integration
Tabular integration works for integrals of the form:
   
f x g x dx

where: Differentiates to
zero in several
steps.
Integrates
repeatedly.


19. 2 x
x e dx

  & deriv.
f x   & integrals
g x
2
x
2x
2
0
x
e
x
e
x
e
x
e



2 x
x e dx 

2 x
x e 2 x
xe
 2 x
e
 C

Compare this with
the same problem
done the other way:


20. Example 5:
2 x
x e dx

u dv uv v du
 
  LIPET
2
u x
 x
dv e dx

2
du x dx
 x
v e

u v v du
 
2
2
x x
x e e x dx
 

2
2
x x
x e xe dx
  u x
 x
dv e dx

du dx
 x
v e

 
2
2
x x x
x e xe e dx
  
2
2 2
x x x
x e xe e C
  
This is easier and quicker to
do with tabular integration!


21. 3
sin
x x dx

3
x
2
3x
6x
6
sin x
cosx

sin x

cos x



0

sin x
3
cos
x x
 2
3 sin
x x
 6 cos
x x
 6sin x
 + C

22. 2 x
x e dx
ò ( )& deriv.
f x ( )& integrals
g x
2
x
2x
2
0
x
e
x
e
x
e
x
e
+
+
-
2 x
x e dx =
ò
2 x
x e 2 x
xe
- 2 x
e
+ C
+
Try the
other
way

23. Questions?