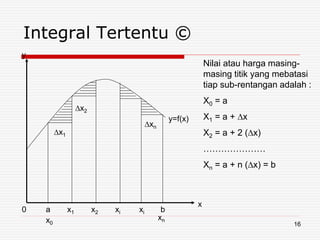
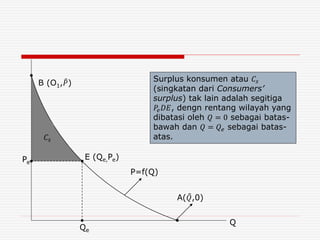
Dokumen ini membahas tentang integral, baik tak tentu maupun tertentu, serta aplikasinya dalam ekonomi, termasuk fungsi biaya, penerimaan, dan produksi. Berbagai kaidah integrasi seperti formula pangkat, logaritmis, dan eksponensial dijelaskan untuk membantu menghitung integral dan menghubungkannya dengan konsep surplus konsumen dan produsen. Contoh kasus disertakan untuk memperjelas penerapan teori ini dalam menentukan biaya total, penerimaan total, dan surplus dalam konteks ekonomi.

1. Integral
1. INTEGRAL TAK TENTU DAN TENTU
(SUATU PENDAHULUAN)
2. Aplikasi dalam Ekonomi

2. Integral tak tentu
 Mengintegralkan suatu fungsi turunan
f(x) berarti adalah mencari integral atau
turunan antinya, yaitu F(x)
 Bentuk umum integral dari f(x) adalah :
  kxFdxxf )()(
Dimana k adalah sembarang konstanta yang nilainya
tidak tentu.
2

3. Integral tak tentu ©
 Contoh
untuk fungsi asal : F(x) = x2 + 5
fungsi turunannya : f(x) = dF(x) / dx = 2x
Jika prosesnya dibalik, maka :
kxkxFdxxf 
2
)()(
3

4. Kaidah- kaidah Integrasi tak tentu
Kaidah 1. Formula Pangkat
k
n
x
dxx
n
n




 1
1
Kaidah 2. Formula Logaritmis
kxdx
x
 ln
1
4

5. Kaidah- kaidah Integrasi tak tentu ©
 Kaidah 3. Formula Eksponensial
 Kaidah 4. Formula Penjumlahan
f(x)ukedue
kedxe
uu
xx




 
kG(x)F(x)
dxxgdxxfdxxgxf

   )()()()(
5

6. Kaidah-kaidah Integrasi tak tentu
©
 Kaidah 5. Formula Perkalian
 Kaidah 6. Formula Substitusi
  0)( ndxxfndxn f(x)
  kuFduufdx
dx
du
uf )()()(
6

7. Penerapan Ekonomi
Pendekatan integral tak tentu dapat diterapkan
untuk mencari persamaan fungsi total dari
suatu variabel ekonomi apabila persamaan
fungsi marginalnya diketahui.
1. Fungsi Biaya
2. Fungsi Penerimaan
3. Fungsi Produksi

8. Fungsi Biaya
 Biaya total 𝐶 = 𝑓(𝑄)
 Biaya marjinal : 𝑀𝐶 = 𝐶′
=
𝑑𝐶
𝑑𝑄
= 𝑓′(𝑄)
 Biaya total tak lain adalah integral
dari biaya biaya marjinal
𝐶 = 𝑀𝐶𝑑𝑄 = 𝑓′ 𝑄 𝑑𝑄

9. Contoh kasus
 Biaya marjinal dari suatu perusahaan
ditunjukkan oleh 𝑀𝐶 = 3𝑄2
− 6𝑄 + 4.
Carilah persamaan biaya total dan biaya
rata-ratanya.
 Biaya total : 𝐶 = 𝑀𝐶𝑑𝑄
= 3𝑄2
− 6𝑄 + 4 𝑑𝑄
 Biaya rata-rata : 𝐴𝐶 =
𝐶
𝑄
= 𝑄2
− 3𝑄 + 4 + 𝑘
𝑄

10.  Konstanta 𝑘 tak lain adalah biaya
tetap. Jika diketahui biaya tetap
tersebut sebesar 4, maka :
 𝐶 = 𝑄3
− 3𝑄2
+ 4𝑄 + 4
 𝐴𝐶 = 𝑄2
− 3𝑄 + 4 + 4
𝑄

11. Fungsi Penerimaan
 Penerimaan total : 𝑅 = 𝑓(𝑄)
 Penerimaan marjinal : 𝑀𝑅 = 𝑅′
=
𝑑𝑅
𝑑𝑄
= 𝑓′(𝑄)
 Penerimaan total tak lain adalah integral
dan penerimaan marjinal
𝑅 = 𝑀𝑅 𝑑𝑄 = 𝑓′ 𝑄 𝑑𝑄

12. Contoh Kasus
 Carilah persamaan penerimaan total dan
penerimaan rata-rata dari suatu perusahaan
jika penerimaan marjinalnya 𝑀𝑅 = 16 − 4𝑄.
 Penerimaan total : 𝑅 = 𝑀𝑅 𝑑𝑄
= 16 − 4𝑄 𝑑𝑄
= 16𝑄 − 2𝑄2
 Penerimaan rata-rata: 𝐴𝑅 =
𝑅
𝑄
= 16 − 2𝑄
 Dalam persamaan penerimaan total kontanta
𝑘 = 0, sebab penerimaan tidak akan ada jika
tak ada barang yang dihasilkan atau terjual.

13. Fungsi Produksi
 Produk total : 𝑃 = 𝑓(𝑋) di mana,
 𝑃 = keluaran; 𝑋 = masukan
 Produk marjinal : 𝑀𝑃 = 𝑃′
=
𝑑𝑃
𝑑𝑋
= 𝑓′(𝑋)
 Produk total tak lain adalah integral
dari produk marjinal
𝑃 = 𝑀𝑃 𝑑𝑋 = 𝑓′
𝑋 𝑑𝑋

14. Contoh kasus
 Produk marjinal sebuah perusahaan dicerminkan oleh
𝑀𝑃 = 18𝑋 − 3𝑋2. Carilah persamaan produk total dan
produk rata-ratanya.
 Produk total : 𝑃 = 𝑀𝑃 𝑑𝑋
 = (18𝑋 − 3𝑋2) 𝑑𝑋
 = 9𝑋2 − 𝑋3
 Produk rata-rata : 𝐴𝑃 =
𝑃
𝑋
= 9𝑋 − 𝑋2
 Dalam persamaan produk total juga konstant 𝑘 = 0,
sebab tidak akan ada barang (P) yang dihasilkn jika
tidak ada bahan (X) yang diolah atau digunakan.

15. Integral Tertentu
 Integral tertentu adalah integral dari suatu fungsi yang
nilai-nilai variabel bebasnya (memiliki batas-batas)
tertentu.
 Integral tertentu digunakan untuk menghitung luas
areal yang terletak di antara kurva y = f(x) dan sumbu
horizontal – x, dalam suatu rentangan wilayah yang
dibatasi oleh x = a dan x =b.
 Bentuk umum :
  )()()()( aFbFxFdxxf
b
a
b
a 
15

16. Integral Tertentu ©
∆x1
∆x2
∆xn
0 a x1 x2 xi xi b
xn
x
y
y=f(x)
Nilai atau harga masing-
masing titik yang mebatasi
tiap sub-rentangan adalah :
X0 = a
X1 = a + ∆x
X2 = a + 2 (∆x)
…………………
Xn = a + n (∆x) = b
x0 16

17. Kaidah- kaidah Integrasi Tertentu
Untuk a < b < c, berlaku :
 






a
b
b
a
a
b
a
b
a
dxxfdxxf
dxxf
aFbFxFdxxf
)()(.3
0)(.2
)()()()(.1
17

18. Kaidah- kaidah Integrasi Tertentu
©

 





bc
a
b
c
b
a
b
a
b
a
b
a
b
a
dxxfdxxfdxxf
dxxgdxxfdxxgxf
dxxfkdxxkf
)()()(.6
)()()()(.5
)()(.4
18

19. Surplus Konsumen
 Surplus konsumen atau CS (singkatan dari
Consumer Surplus)
 Surplus konsumen mencerminkan suatu
keuntungan lebih atau surplus yang
dinikmati oleh konsumen tertentu berkenaan
dengan tingkat harga pasar.
 Fungsi permintaan (P) = f (Q) menunjukkan
jumlah suatu barang yang akan dibeli oleh
konsumen pada tingkat harga tertentu.

20. Surplus konsumen
 Jika tingkat harga pasar adalah Pe, maka bagi
konsumen tertentu yang sebetulnya mampu
dan bersedia membayar dengan harga yang
lebih tinggi dari Pe.
 Hal ini akan merupakan keuntungan baginya,
sebab ia cukup membayar barang tadi dengan
harga Pe. Secara geometri, besarnya surplus
konsumen ditunjukkan oleh luar daerah di
bawah kurva permintaaan tetapi di atas
tingkat harga pasar.

21. B (O1, 𝑃)
𝐶𝑠
Pe
E (Qe,Pe)
P=f(Q)
A( 𝑄,0)
Qe
Q
Surplus konsumen atau 𝐶𝑠
(singkatan dari Consumers’
surplus) tak lain adalah segitiga
𝑃𝑒 𝐷𝐸, dengn rentang wilayah yang
dibatasi oleh 𝑄 = 0 sebagai batas-
bawah dan 𝑄 = 𝑄 𝑒 sebagai batas-
atas.

22.  Besarnya surplus konsumen adalah :
𝐶𝑠 =
0
𝑄𝑒
𝑓(𝑄) 𝑑𝑄 − 𝑄 𝑒 𝑃𝑒
 Dalam hal fungsi permintaan berbentuk 𝑃 =
𝑓(𝑄) atau
𝐶𝑠 =
𝑃𝑒
𝑃
𝑓 𝑃 𝑑𝑃
 Dalam hal fungsi permintaan berbentuk 𝑄 =
𝑓(𝑃); 𝑃 adalah nilai 𝑃 untuk 𝑄 = 0 atau
penggal kurva permintaan pada sumbu harga

23. Dengan demikian :
𝐶𝑠 =
0
𝑄𝑒
𝑓(𝑄) 𝑑𝑄 − 𝑄 𝑒 𝑃𝑒 =
𝑃𝑒
𝑃
𝑓 𝑃 𝑑𝑃

24. Contoh Kasus
 Fungsi permintan akan suatu barang
ditunjukkan oleh persamaan 𝑄 = 48 −
0,03𝑃2
. Hitunglah surplus konsumen
jika tingkat harga pasar adalah 30.

25. Jawab
 𝑄 = 48 − 0,03𝑃2
 Jika 𝑃 = 0, 𝑄 = 48
 Jika 𝑄 = 0, 𝑃 = 40 ≡ 𝑃
 Jika 𝑃 ≡ 𝑃𝑒 = 30, 𝑄 ≡ 𝑄 𝑒 = 40
 𝐶𝑠 = 𝑃𝑒
𝑃
𝑓(𝑃) 𝑑𝑃 = 30
40
(48 − 0,03𝑃2
) 𝑑𝑃
= 48𝑃 − 0,01(40)3 40
30
= 48 40 −

26. Cs40
30
0 21 48
E
Q
P

27. Surplus Produsen
 Surplus Produsen atau Ps (singkatan dari
Producers’ Surplus)
 Mencerminkan suatu keuntungan lebih
atau surplus yang dinikmati oleh
produsen tertentu berkenaan dngan
tingkat harga pasar dari barang yang
ditawarkan
 Fungsi penawaran 𝑃 = 𝑓(𝑄) menunjukkan
jumlah suatu barang yang akn dijual oleh
produsen pada tingkat harga tertentu

28. Surplus Produsen
 Jika tingkat harga pasar adalah 𝑃𝑒, maka
bagi produsen tertentu yang sebetulnya
bersedia menjual dengan harga yang
lebih rendah dari 𝑃𝑒
 Hal ini merupakan keuntungan baginya,
sebab ia dapat menjual barangnya
dengan harga 𝑃𝑒. Secara geometri,
besarnya surplus produsen ditunjukkan
oleh luas area di atas kurva penawaran
tetapi di bawah tingkat harga pasar.

29. P
Pe
P=f(Q)
E(Qe,Pe)
D(0, 𝑃)
Qe
Q
Surplus produsen (Ps)
0
Surplus produsen atau Ps
(singkatan dari Producers’
surplus) tak lain adalah
segitiga 𝑃𝑒 𝐷𝐸, dengan
rentang wilayah yang
dibatasi oleh 𝑄 = 0 sebagai
batas bawah dan 𝑄 = 𝑄 𝑒
sebagai batas-atas.

30.  Besarnya surplus produsen adalah :
𝑃𝑠 = 𝑄 𝑒 𝑃𝑒 −
0
𝑄𝑒
𝑓 𝑄 𝑑𝑄
 Dalam hal fungsi penawaran berbentuk 𝑃 =
𝑓(𝑄)
𝑃𝑠 =
𝑃
𝑃𝑒
𝑓 𝑃 𝑑𝑃
 Dalam hal fungsi penawaran berbentuk 𝑄 =
𝑓(𝑃); 𝑃 adalah nilai 𝑃 untuk 𝑄 = 0, atau
penggal kurva penawaran pada sumbu harga

31. Dengan demikian :
𝑃𝑠 = 𝑄 𝑒 𝑃𝑒 −
0
𝑄 𝑒
𝑓 𝑄 𝑑𝑄 =
𝑃
𝑃𝑒
𝑓 𝑃 𝑑𝑃

32. Contoh Kasus
 Seorang produsen mempunyai fungsi
penawaran 𝑃 = 0,50𝑄 + 3. Berapa
surplusprodusen itu bila tingkat harga
keseimbangan di pasar adalah 10?
 𝑃 = 0,50𝑄 + 3 → 𝑄 = −6 + 2𝑃
 𝑃 = 0 → 𝑄 = −6
 𝑄 = 0 → 𝑃 = 3 ≡ 𝑃
 𝑃𝑒 = 10 → 𝑄 𝑒 = 14

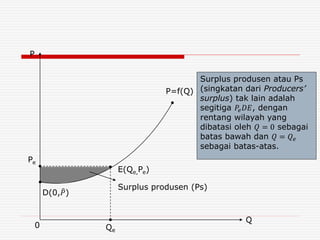
33. Cara pertama
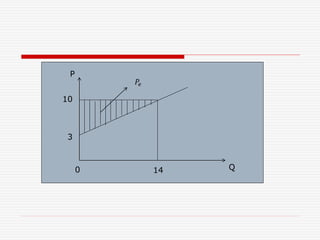
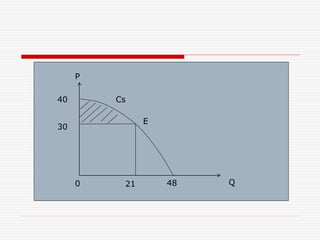
𝑃𝑠 = 𝑄 𝑒 𝑃𝑒 − 0
𝑄 𝑒
𝑓 𝑄 𝑑𝑄 = 14 10 − 0
14
(0,50𝑄 + 3) 𝑑𝑄
= 140 − [0,25𝑄2 + 3𝑄] 14
0
= 140 − 0,25 14 2 + 3 14 − 0,25(0)2+3(0)
= 140 − 91 − 0 = 49

34. Cara Kedua
𝑃𝑠 = 𝑃
𝑃𝑒
𝑓(𝑃) 𝑑𝑃 = 3
10
(−6 + 2𝑃) 𝑑𝑃
= −6𝑃 + 𝑃2 10
3
= −6 10 + 102 − −6 3 + 32}
= 40 − −9 = 49

35. P
10
3
0 14 Q
𝑃𝑒