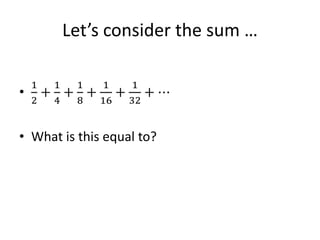
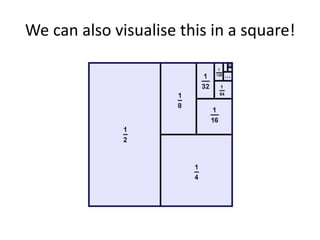
The document discusses infinite geometric series and uses them to prove that 0.999... equals 1. It introduces the infinite geometric series 1/2 + 1/4 + 1/8 + ..., shows that its sum is 1, and derives the general formula for calculating the sum of an infinite geometric series. It then represents 0.999... as the infinite geometric series 0.9 + 0.09 + 0.009 + ..., applies the formula to show its sum is 1, and concludes that 0.999... therefore equals 1.

1. The surprising flavour of
Infinite geometric series

2. Let’s consider the sum …
•
1
2
+
1
4
+
1
8
+
1
16
+
1
32
+ ⋯
• What is this equal to?

3. Let’s watch this video to get an idea

4. So this sum is actually equal to 1!

5. We can also visualise this in a square!

6. How do we calculate the sum?
• We can prove that the sum of the infinite
geometric series exists if the ratio is a number
between (but not including) -1 and 1, and r
should not be equal to 0. The sum is given by
the formula:
𝑘=0
∞
𝑎𝑟 𝑘
= 𝑎 + 𝑎𝑟 + 𝑎𝑟2
+ 𝑎𝑟3
+ ⋯ =
𝑎
1 − 𝑟

7. Can we use our knowledge to
examine whether
0.999… is actually equal to 1?

8. Does 0.999… equal 1 ?
• We can write a recurring decimal as a sum like
this:
• 0.999… = 0.9 + 0.09 + 0.009 + …
= 9×0.11
+9×0.12
+ 9×0.13
+ ⋯
= 9×(0.11
+ 0.12
+ 0.13
+ ⋯)
this is an infinite geometric series
with first term 0.1 and ratio 0.1
= 9 ×
0.1
1−0.1
= 9 ×
0.1
0.9
=
0.9
0.9
= 1

9. So YES!
0.999…. = 1