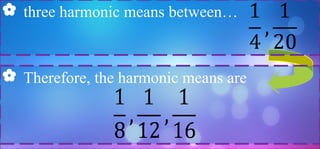
The document provides information about harmonic sequences and the Fibonacci sequence. It discusses how harmonic sequences were first proven in the 14th century but later fell into obscurity until proofs in the 17th century. It also explains that harmonic sequences were used by architects for proportions. An example is given of obtaining harmonic tones on a violin string. It then discusses harmonic means and how to determine the nth term of a harmonic sequence. Finally, it provides background on the Fibonacci sequence, including how it was discovered by Leonardo Fibonacci and that Fibonacci numbers appear in natural patterns.

2. A Brief History about the Harmonic Sequence
Harmonic Series was first proven in the 14th
century by Nicole Oresme, but this
achievement fell into obscurity. Proofs were given in the 17th
century by Pietro
Mengoli, Johann Bernoulli, and Jacob Bernoulli.
Harmonic sequences have had a certain popularity with architects, particularly
in the Baroque period, when architects used them to establish the proportions of
floor plans, of elevations, and to establish harmonic relationship between both
interior and exterior architectural details of churches and palaces.

3. A violin’s first harmonic tone is obtained by lightly plucking the string at its
midpoint. The second harmonic tone is obtained by plucking it one-third the
way down and so on. In mathematical form this example is shown as:
A n example of a harmonic sequence is…

4. Notice that the reciprocals of the terms form the
arithmetic sequence…
2, 3, 4, 5, …, n, …

5. What is Harmonic Mean?
Harmonic means are terms that are between
any two nonconsecutive terms of a harmonic
sequences.

6. Below is an example of a harmonic mean…
Why?
Because 1/3
is between ½,
¼.

7. Below is an example of a harmonic mean…
Why?
Because 1/3
and ¼ is
between ½,
1/5.

8. How can we determine the nth term of a
harmonic sequence?
 Consider the reciprocals of the given terms,
then find the nth term of the resulting
arithmetic sequence, and then take its
reciprocal.

9. Let’s practice, shall we?

10.  Find the 10th
term of the harmonic sequence

11.  10th
term of
 Get the reciprocal: 2, 4, 6, 8
 Use the formula an = a1 + (n – 1)d

12.  10th
term of
 Substituting we have…
 an = 2 + (10 – 1)2 = 2 + (9)2 = 20
Therefore, is the 10th
term of the harmonic sequence

13.  Insert three harmonic means between…

14.  three harmonic means between…
 Reciprocal of the following: 4 and 20
 Substituting these values in the arithmetic
formula we have 20 = 4 + (5 – 1)d = 4.

15.  three harmonic means between…
 We now have the common difference d
which is 4. Now we simply add 4 to the other
values to get the harmonic means.

16.  three harmonic means between…
 Therefore, the harmonic means are

17. Think about this…
Interesting number patterns are all around us. For example, the scales of
a pineapple form a double set of spirals – one going clockwise, and one
going counterclockwise. When we count theses spirals, we see three
distinct families of spirals with usually 5, and 8, or 8 and 13, or 13 and
21 spirals.
Can you see a specific pattern in the sequence of numbers 5, 8, 13, 21,
…?

18. The numbers 5, 8, 13, 21,… are called
Fibonacci numbers. They are terms of the
Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34,
55,…

19. A Brief History about the Fibonacci sequence
Fibonacci Series is a series of numbers in which each member is the sum of the
two preceding numbers. For example, a series beginning 0, 1 ... continues as 1,
2, 3, 5, 8, 13, 21, and so forth.
The series was discovered by the Italian mathematician Leonardo Fibonacci
(circa 1170-c. 1240), also called Leonardo of Pisa. Fibonacci numbers have
many interesting properties and are widely used in mathematics. Natural
patterns, such as the spiral growth of leaves on some trees, often exhibit the
Fibonacci series.

20. Leonardo Fibonacci
Founder of the Fibonacci sequence

21. Find the sum of the first five odd terms of
the Fibonacci sequence; that is,
F1 + F3+ F5 + F7 + F9.

22. F1 + F3+ F5 + F7 + F9 (Remember the basic pattern)
= 1 + 2 + 5 + 13 + 34
= 55
The sum of the first n odd terms of the Fibonacci
sequence is F2n; that is, F1 + F3 + … + F 2n-1 = F2n.

23. Remember that…
A sequence of numbers whose reciprocals form an arithmetic
sequence is called a harmonic sequence.
The terms between any two nonconsecutive terms of a
harmonic sequence are called harmonic means.
A sequence of numbers in which the first two terms are 1 and
each terms is the sum of the preceding terms is called Fibonacci
sequence.

24. If you are patient in one moment of anger, you
will escape a hundred days of sorrow.
 Chinese Proverb