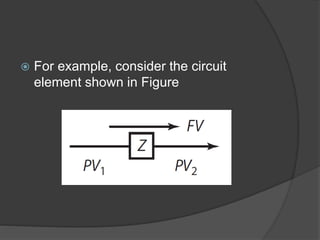
The document discusses the concept of impedance in electrical circuits, defined as the ratio of voltage phasor to current phasor. It explains how positive and negative phase angles correspond to specific positions of the phasor and describes the behavior of capacitors and inductors regarding voltage and current timing. Additionally, it highlights the mathematical differentiation of sinusoidal functions and the representation of component impedance.

1. Submitted by
Gopi chand

2. IMPEDENCE
o In an electrical circuit the impedance of a
component is defined as the ratio of the voltage
phasor v, across the component over the current
phasor I , through the component.

3. The impedance phasor for the capacitor, inductor,
and resistor are summarized in table below

4.  Positive phase occurs when the phasor is rotated
in the counter clockwise direction beginning
from the positive real axis
 When the phasor is lined up with the positive
imaginary axis (vertically upward) 90° of the
phase has been accumulated.
 When the phasor is pointing leftward,180° of the
phase has been accumulated.
 When the phasor is pointing downward along the
negative imaginary axis, 270° or -90 ° of the
phase has been accumulated.

5.  Keeping in mind that impedance is voltage
divided by current, a positive imaginary
component indicates voltage leading current, and
a negative imaginary component indicates
voltage lagging current.
 Because j occurs in the denominator of the
capacitor impedance, the capacitor voltage lags
its current by 90°.
 Similarly, because j occurs in the numerator of
the inductor impedance, the inductor voltage
leads its current by 90°.

6.  Consider the sinusoid x(t) = sin ωt . If we
differentiate x(t) analytically with respect to
time, we obtain
X ‘(t) =d(sin(ωt))/dt = ω’cos(ωt)
 Further more, since cos λ = sin(λ + 90°)ω ,
the right side of X ‘(t) may be written as ω‘
sin(ωt + 90°) or simply jω’ sin(ωt)
 This means that differentiation of a
sinusoid of frequency ω is the same as
multiplication of the sinusoid by j ω .

7.  The impedance of a component is often
represented as ZX, where X is the
component name or description.
 In terms of the potential and flow variables,
the impedance of a component is defined as
the ratio of the potential variable to the flow
variable
1

8.  For example, consider the circuit
element shown in Figure

9.  In accordance with Equation 1, the
impedance of the circuit element
becomes
Z = PV1 - PV2/FV
=ΔPV/FV