Download as PDF, PPTX
Uploaded byJessore University of Science & Technology
CAPACITORS AND INDUCTORS
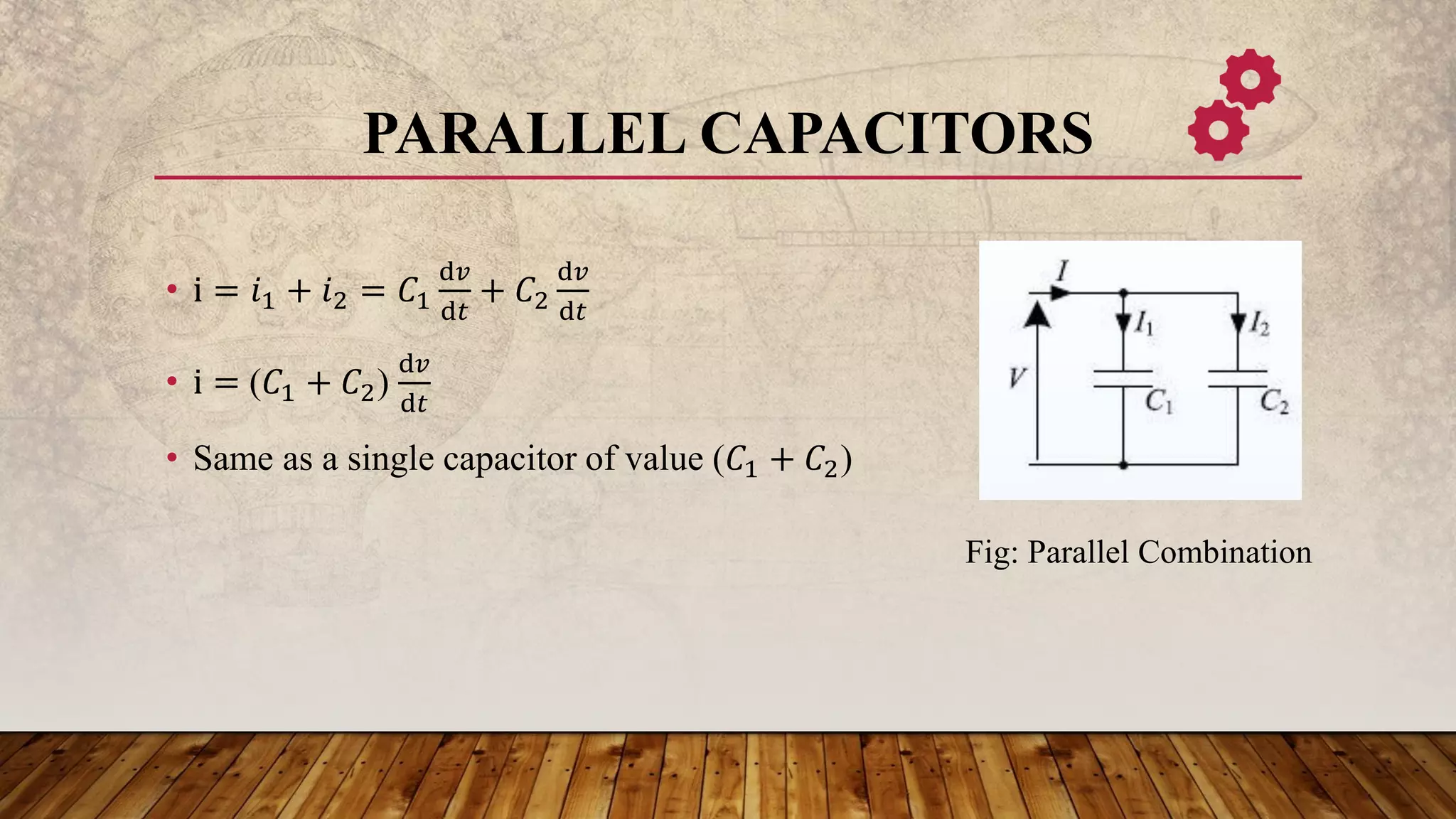
The document provides a comprehensive overview of capacitors and inductors, detailing their energy storage mechanisms, equations governing their behavior, and how they operate in series and parallel combinations. It outlines the formulas for current-voltage relationships, energy storage, and the differences in behavior for AC and DC circuits. Additionally, it includes examples and typical values for capacitors and inductors, as well as calculations for combined inductances.
More Related Content
Similar to CAPACITORS AND INDUCTORS
CAPACITORS AND INDUCTORS
- 1. CAPACITORS AND INDUCTORS FUNDAMENTALS OF ELECTRICALAND ELECTRONICS ENGINEERING
- 2. • Element thatstores energy in an electric field. CAPACITOR Fig: Circuit Symbol Fig: Capacitor Model
- 3.
- 4. • 𝜈 ∝𝑞 • 𝜈 = 𝑑 𝐴 𝜖 𝑞 • 𝐶 = 𝐴 𝜖 𝑑 • Hence, q=Cv • Capacitor Equation: ⅈ = ⅆ𝑞 ⅆ𝑡 = 𝐶 ⅆ𝜈 ⅆ𝑡 • Here, v= Voltage q= Quantity of charge C= Capacitance i= Current ∈= Permittivity GENERAL EQUATIONS OF CAPACITOR
- 5. • ⅈ =𝑖1 + 𝑖2 = 𝐶1 ⅆ𝑣 ⅆ𝑡 + 𝐶2 ⅆ𝑣 ⅆ𝑡 • ⅈ = (𝐶1 + 𝐶2) ⅆ𝑣 ⅆ𝑡 • Same as a single capacitor of value (𝐶1 + 𝐶2) PARALLEL CAPACITORS Fig: Parallel Combination
- 6. • ⅆ𝜈 ⅆ𝑡 = ⅆ 𝑣1+𝑣2 ⅆ𝑡 = ⅆ𝜈1 ⅆ𝑡 + ⅆ𝑣2 ⅆ𝑡 = ⅈ 𝐶1 + ⅈ 𝐶2 = ⅈ 1 𝐶1 + 1 𝐶2 =ⅈ 𝐶1+𝐶2 𝐶1 𝐶2 • ⅈ = 𝐶1 𝐶2 𝐶1+𝐶2 ⅆ𝜈 ⅆ𝑡 • Same as a single capacitor of value 𝐶1 𝐶2 𝐶1+𝐶2 SERIES CAPACITORS Fig: Series Combination
- 7.
- 8.
- 9. Energy stored incapacitors: 1. For capacitor 𝐶1: 0 Joules 2. For capacitor 𝐶2: 𝐸 𝐶2 = 1 2 𝐶2 𝑣2 = 1 2 1 × 10−6 × 102 = 50𝜇 Joules 3. For capacitor 𝐶3: 𝐸 𝐶3 = 1 2 𝐶3 𝑣2 = 1 2 10 × 10−6 × 102 = 500𝜇 Joules EXAMPLE
- 10. SYNOPSIS • Stores energyin an electric field. • Current –voltage relationship: ⅈ = 𝐶 ⅆ𝜈 ⅆ𝑡 • Energy stored: 𝐸 = 1 2 𝐶𝑣2 • Unit: Farad • Typical capacitor values are in mF to pF. • In DC, acts as an open circuit.
- 11. • Coil whichstores energy in the magnetic field. INDUCTORS Fig: Inductor Model Fig: Circuit Symbol
- 12. • According tothe figure: 𝜙 = 𝜇𝑁𝐴 𝑙 ⅈ Where, 𝜙= Magnetic flux • From Farad’s Law: 𝜈 = 𝑁 ⅆ𝜙 ⅆ𝑡 = 𝜇𝑁2 𝐴 𝑙 ⋅ ⅆⅈ ⅆ𝑡 = 𝐿 ⅆⅈ ⅆ𝑡 Where, L= Inductance = 𝜇𝑁2 𝐴 𝑙 GENERAL EQUATIONS OF INDUCTOR
- 13. • 𝑣 =𝜈1 + 𝜈2 = 𝐿1 ⅆⅈ ⅆ𝑡 + 𝐿2 ⅆⅈ ⅆ𝑡 =(𝐿1+ 𝐿2) ⅆⅈ ⅆ𝑡 • Same as a single inductor of value: 𝐿1+ 𝐿2 PARALLEL INDUCTORS Fig: Parallel Combination
- 14. • ⅆ𝑖 ⅆ𝑡 = ⅆ 𝑖1+𝑖2 ⅆ𝑡 = ⅆ𝑖1 ⅆ𝑡 + ⅆ𝑖2 ⅆ𝑡 = v 𝐿1 + v 𝐿2 = 𝑣 1 𝐿1 + 1 𝐿2 =𝑣 𝐿1+𝐿2 𝐿1 𝐿2 • 𝑣 = 𝐿1 𝐿2 𝐿1+𝐿2 ⅆ𝑖 ⅆ𝑡 • Same as a single Inductor of value 𝐿1 𝐿2 𝐿1+𝐿2 SERIES INDUCTORS Fig: Series Combination
- 15.
- 16. Q: Two coilsconnected in series have a self-inductance of 20mH and 60mH respectively. The total inductance of the combination was found to be 100mH. Determine the amount of mutual inductance that exists between the two coils assuming that they are aiding each other. Ans: 𝐿 𝑇 = 𝐿1 + 𝐿2 ± 2𝑀 100= 20 + 60 + 2M M= 10 mH EXAMPLE
- 17. • Stores energyin a magnetic field. • Current-voltage relationship: 𝜈 = 𝐿 ⅆⅈ ⅆ𝑡 . • Energy stored: 𝐸 = 1 2 𝐿𝑖2 . • In DC, Behaves like a short circuit. SYNOPSIS
- 18. THANK YOU FOR STAYINGWITH US THROUGH THE PRESENTATION