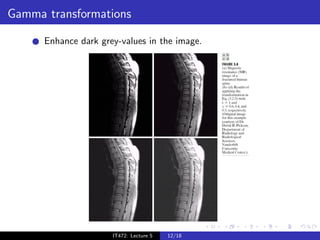
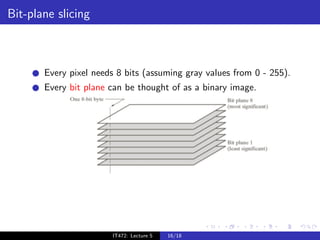
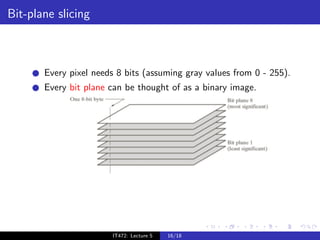
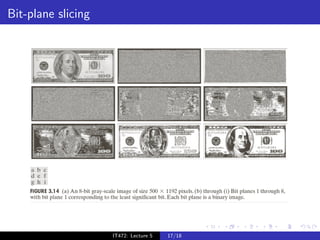
The document discusses spatial transformations and intensity transformations for image enhancement. Spatial transformations include scaling, rotation, translation, and shear, which can be represented using a matrix. Intensity transformations modify pixel intensities based on a transfer function and are used for contrast enhancement. Common transformations include image negative, powers, and logarithms. The appropriate transformation depends on the image content and which intensity values need enhancement.

1. Spatial Transformations
IT472: Digital Image Processing, Lecture 5

2. Spatial Transformations
Affine transformations of the support of the image f (x, y )
Scaling: x = cx x and y = cy y → f (x , y ) = f (x, y ).
Rotation: x = x cos θ − y sin θ and
y = x cos θ + y sin θ → f (x , y ) = f (x, y ).
Translation: x = x + tx and
y = y + ty → f (x , y ) = f (x, y ).
Shear: x = x + sy y and y = y → f (x , y ) = f (x, y ).
All these collected together can be represented in a matrix
form using Homogeneous coordinates, as follows:
    
x cos θ/cx /1 sin θ/sy /0 0/tx x
 y  =  − sin θ/sx /0 cos θ/cy /1 0/ty   y  (1)
1 0 0 1 1
IT472: Lecture 5 2/18

3. Spatial Transformations
Affine transformations of the support of the image f (x, y )
Scaling: x = cx x and y = cy y → f (x , y ) = f (x, y ).
Rotation: x = x cos θ − y sin θ and
y = x cos θ + y sin θ → f (x , y ) = f (x, y ).
Translation: x = x + tx and
y = y + ty → f (x , y ) = f (x, y ).
Shear: x = x + sy y and y = y → f (x , y ) = f (x, y ).
All these collected together can be represented in a matrix
form using Homogeneous coordinates, as follows:
    
x cos θ/cx /1 sin θ/sy /0 0/tx x
 y  =  − sin θ/sx /0 cos θ/cy /1 0/ty   y  (1)
1 0 0 1 1
IT472: Lecture 5 2/18

4. Spatial Transformations
Affine transformations of the support of the image f (x, y )
Scaling: x = cx x and y = cy y → f (x , y ) = f (x, y ).
Rotation: x = x cos θ − y sin θ and
y = x cos θ + y sin θ → f (x , y ) = f (x, y ).
Translation: x = x + tx and
y = y + ty → f (x , y ) = f (x, y ).
Shear: x = x + sy y and y = y → f (x , y ) = f (x, y ).
All these collected together can be represented in a matrix
form using Homogeneous coordinates, as follows:
    
x cos θ/cx /1 sin θ/sy /0 0/tx x
 y  =  − sin θ/sx /0 cos θ/cy /1 0/ty   y  (1)
1 0 0 1 1
IT472: Lecture 5 2/18

5. Spatial Transformations
Affine transformations of the support of the image f (x, y )
Scaling: x = cx x and y = cy y → f (x , y ) = f (x, y ).
Rotation: x = x cos θ − y sin θ and
y = x cos θ + y sin θ → f (x , y ) = f (x, y ).
Translation: x = x + tx and
y = y + ty → f (x , y ) = f (x, y ).
Shear: x = x + sy y and y = y → f (x , y ) = f (x, y ).
All these collected together can be represented in a matrix
form using Homogeneous coordinates, as follows:
    
x cos θ/cx /1 sin θ/sy /0 0/tx x
 y  =  − sin θ/sx /0 cos θ/cy /1 0/ty   y  (1)
1 0 0 1 1
IT472: Lecture 5 2/18

6. Spatial Transformations
Affine transformations of the support of the image f (x, y )
Scaling: x = cx x and y = cy y → f (x , y ) = f (x, y ).
Rotation: x = x cos θ − y sin θ and
y = x cos θ + y sin θ → f (x , y ) = f (x, y ).
Translation: x = x + tx and
y = y + ty → f (x , y ) = f (x, y ).
Shear: x = x + sy y and y = y → f (x , y ) = f (x, y ).
All these collected together can be represented in a matrix
form using Homogeneous coordinates, as follows:
    
x cos θ/cx /1 sin θ/sy /0 0/tx x
 y  =  − sin θ/sx /0 cos θ/cy /1 0/ty   y  (1)
1 0 0 1 1
IT472: Lecture 5 2/18

7. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

8. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

9. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

10. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

11. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

12. Implementation issues
For a given affine transformation matrix A, A · (x, y )t is not
always an integer.
Is it possible that due to rounding off
A · (x1 , y1 )t = A · (x2 , y2 )t
Solution:
Instead of using a forward mapping, let’s work with the inverse
mapping.
A−1 : (x , y )t → (x, y )t
We can scan the output image coordinates and see where they
come from, and accordingly assign them grey values.
IT472: Lecture 5 3/18

13. Examples
Figure: (top-left) Image of Lena (top-right) Image rotated by 23◦
(bottom-left) Shear sx = 1.2, (bottom-right) Shear sx = −1.2
IT472: Lecture 5 4/18

14. End of Chapter 2
Chapter 3: Intensity transformations and Spatial filtering
(Image enhancement in the spatial domain)
IT472: Lecture 5 5/18

15. End of Chapter 2
Chapter 3: Intensity transformations and Spatial filtering
(Image enhancement in the spatial domain)
IT472: Lecture 5 5/18

16. Image enhancement
Image enhancement is a pre-processing step that makes the
input image better suited for further processing. For example,
for segmentation, recognition, or simply better for somebody
to view the image.
Intensity transformations: Depends only on the intensity value
at a point: g (x, y ) = T [f (x, y )], can be also written as
s = T [r ], where r and s are the input and output grey values
respectively.
IT472: Lecture 5 6/18

17. Image enhancement
Image enhancement is a pre-processing step that makes the
input image better suited for further processing. For example,
for segmentation, recognition, or simply better for somebody
to view the image.
Intensity transformations: Depends only on the intensity value
at a point: g (x, y ) = T [f (x, y )], can be also written as
s = T [r ], where r and s are the input and output grey values
respectively.
IT472: Lecture 5 6/18

18. Intensity transformations
Image negative: s = L − 1 − r
Powers, nth roots, Log transformations etc..
IT472: Lecture 5 7/18

19. Intensity transformations
Image negative: s = L − 1 − r
Powers, nth roots, Log transformations etc..
IT472: Lecture 5 7/18

20. Intensity transformations
Image negative: s = L − 1 − r
Powers, nth roots, Log transformations etc..
IT472: Lecture 5 7/18

21. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

22. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

23. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

24. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

25. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

26. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

27. Applications of Intensity transformations
Intensity transformations are used frequently for Contrast
enhancement.
Contrast measures how much the object color/grey value
differs from its surroundings.
Objective definitions:
Weber contrast: I −Ib
Ib
Michelson contrast: IImax −Imin
max +I
min
M N
RMS contrast: i=1 j=1 (Iij − ¯)2
I
Appropriate transformation must be chosen depending on
what grey values you want to enhance and what is the
content of the input image.
IT472: Lecture 5 8/18

28. Contrast enhancement
We will frequently use the log-transformation to view the
Fourier spectrum of an image.
IT472: Lecture 5 9/18

29. Contrast enhancement
We will frequently use the log-transformation to view the
Fourier spectrum of an image.
IT472: Lecture 5 9/18

30. Gamma transformations
s = cr γ
IT472: Lecture 5 10/18

31. Gamma transformations
Gamma correction in CRTs
IT472: Lecture 5 11/18

32. Gamma transformations
Enhance dark grey-values in the image.
IT472: Lecture 5 12/18

33. Gamma transformations
Enhance brighter grey-values in the image.
IT472: Lecture 5 13/18

34. Contrast stretching
IT472: Lecture 5 14/18

35. Intensity slicing
IT472: Lecture 5 15/18

36. Bit-plane slicing
Every pixel needs 8 bits (assuming gray values from 0 - 255).
Every bit plane can be thought of as a binary image.
IT472: Lecture 5 16/18

37. Bit-plane slicing
Every pixel needs 8 bits (assuming gray values from 0 - 255).
Every bit plane can be thought of as a binary image.
IT472: Lecture 5 16/18

38. Bit-plane slicing
Every pixel needs 8 bits (assuming gray values from 0 - 255).
Every bit plane can be thought of as a binary image.
IT472: Lecture 5 16/18

39. Bit-plane slicing
IT472: Lecture 5 17/18

40. Bit-plane slicing
Can be used for image compression.
Figure: (top row) Reconstructions from bit planes (bottom) Original
image
IT472: Lecture 5 18/18