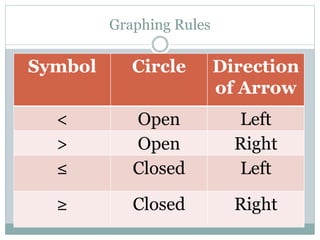
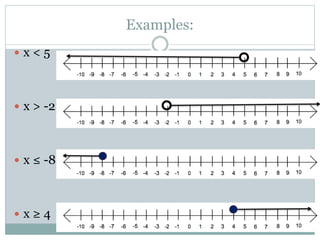
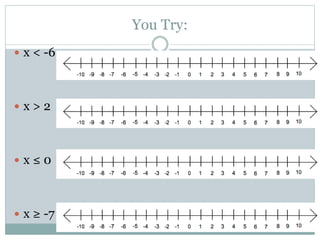
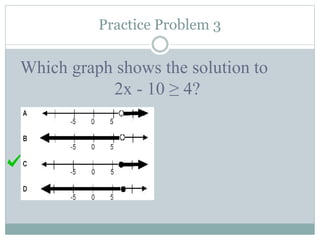
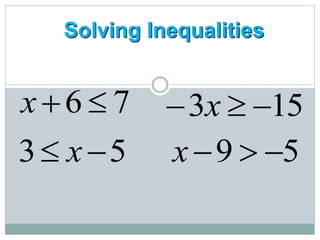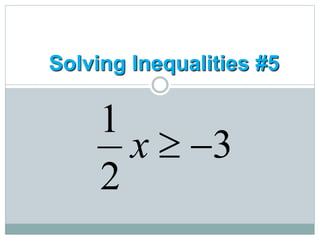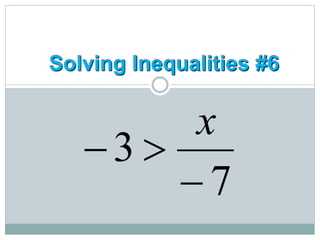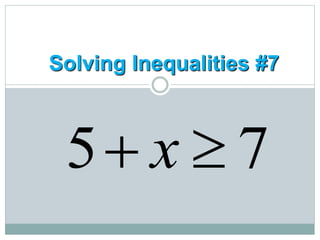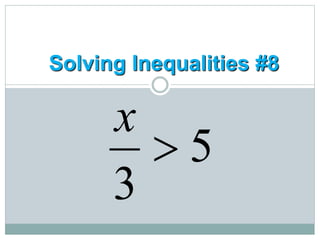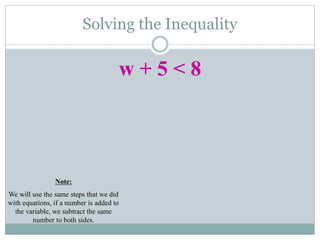
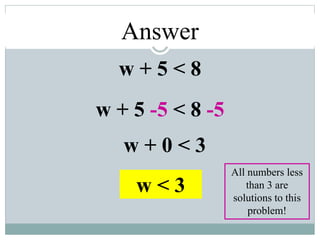
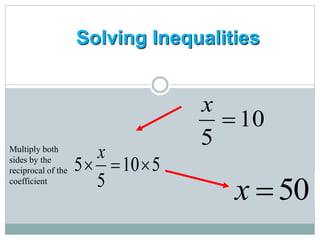
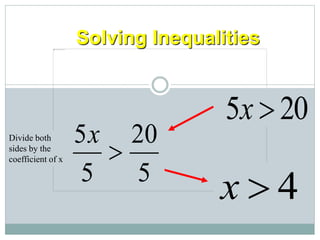
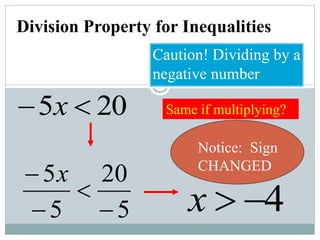
- Students learn to represent inequalities on a number line using different signs such as <, ≤, >, ≥. - They learn to solve inequalities algebraically using the same steps as solving equations, such as adding/subtracting the same number to both sides. - A key rule is that if multiplying or dividing by a negative number, the inequality sign must be switched (e.g. from < to >). - Examples of solving multi-step inequalities and real-world word problems are provided to illustrate the concepts and skills.

1. Solving Inequalities

2. Learning objectives
 Students are able to draw a number line to represent
the values of inequalities.
 Students are able to solve inequalities algebraically.

3. Inequality Signs
An inequality is like an equation, but
instead of an equal sign (=) it has one of
these signs:
< : less than
≤ : less than or equal to
> : greater than
≥ : greater than or equal to

4. “x < 5”
means that whatever value x has,
it must be less than 5.
What could x be?

5. “x ≥ -2”
means that whatever value x has,
it must be greater than or equal to -2.
What could x be?

6. Graphing Rules
Symbol Circle Direction
of Arrow
< Open Left
> Open Right
≤ Closed Left
≥ Closed Right

7. Examples:
 x < 5
 x > -2
 x ≤ -8
 x ≥ 4

8. You Try:
 x < -6
 x > 2
 x ≤ 0
 x ≥ -7

10. Solving the Inequality
w + 5 < 8
Note:
We will use the same steps that we did
with equations, if a number is added to
the variable, we subtract the same
number to both sides.

11. Answer
w + 5 < 8
w + 5 -5 < 8 -5
w + 0 < 3
w < 3
All numbers less
than 3 are
solutions to this
problem!

12. Now you try it!
8 + r ≥ -2
x - 2 > -2
4 + y ≤ 1
7 > x – 5
x + 2 ≤ 3

13. Answers to Practice Problems:
8 + r ≥ -2
8 -8 + r ≥ -2 -8
r + 0 ≥ -10
w ≥ -10
All numbers from -10 and
up (including
-10) make this problem
true!
x - 2 > -2
x - 2 + 2 > -2 + 2
x + 0 > 0
x > 0
All numbers greater than 0
make this problem true!
4 + y ≤ 1
4 - 4 + y ≤ 1 - 4
y + 0 ≤ -3
y ≤ -3
All numbers from -3
down (including -3)
make this problem
true!

14. Answers to Practice Problems:
x - 5 > 7 x + 2 ≤ 3
x – 5 + 5 > 7 + 5
x + 0 > 12
x > 12
12
0
x + 2 - 2 ≤ 7 - 2
x + 0 ≤ 5
x ≤ 5
0 5

16. Solving Inequalities
10
5

x
5
10
5
5 


x
50

x
Multiply both
sides by the
reciprocal of the
coefficient

17. Solving Inequalities
Division Property for Inequalities
20
5 
x
5
20
5
5

x
4

x
Divide both
sides by the
coefficient of x

18. Solving Inequalities!
 Solving inequalities is the same as solving equations.
 There are only 2 things you need to know…
 1.) If you multiply or divide by a negative number you must
switch the sign.
-7x < 21
-7 -7
x > -3
 2.) You will graph your solutions.
Dividing by a
negative means
switch the sign!!

19. Special Case 1: Switching the Signs
 When solving inequalities, if you multiply or
divide by a negative you must switch the signs.
 Switching the signs:
 Less than becomes Greater than < switches to >
 Greater than becomes Less than > switches to <
 Less than or equal to becomes Greater than or equal to
≤ switches to ≥
 Greater than or equal to becomes Less than or equal to
≥ switches to ≤

20. Division Property for Inequalities
Caution! Dividing by a
negative number
20
5 
 x
5
20
5
5



 x
4


x
Notice: Sign
CHANGED
Same if multiplying?

21. Multiplication Property for
Inequalities
Caution! When you
multiply by a negative
number…
…the sign
CHANGES
YES
!
-x > 2
5
(-5 )-x > 2(-5)
1 5
x < -10

22. Solving Inequalities
Let’s try some on our
own …… ready?

23. Solving Inequalities
7
6 

x
5
3 
 x
15
3 

 x
5
9 


x

24. 1. x ≤ 1
2. 8 ≤ x or x ≥
8
Answers for #1 - #4
3. x ≤ 5
4. x > 4

25. Solving Inequalities #5
3
2
1


x

26. Solving Inequalities #6
7
3



x

27. Solving Inequalities #7
7
5 
 x

28. Solving Inequalities #8
5
3

x

29. Answers for #5 - #8
5. x ≥ -6
6. 21 < x or x > 21
7. x ≥ 2
8. x > 15

31. Solving Inequalities
 Follow same steps used to solve equations:
3x + 4 < 13
- 4 -4
3x < 9
3 3
x < 3

32. Practice Problem 1
−4 − 5v < −29

33. Practice Problem 2
−2 + r > −1
9

34. Practice Problem 3
Which graph shows the solution to
2x - 10 ≥ 4?

37. Real-Life Application
Hint: 90 x 6
90% = 540 pts.
You are taking a history
course in which your grade
is based on six 100 point
tests. To earn an A in class,
you must have a total of at
least 90%. You have
scored an 83, 89, 95, 98,
and 92 on the first five
tests. What is the least
amount of points you can
earn on the sixth test in
order to earn an A in the
course?
83+89+95+98+92= 457
457 - 457 + T ≤ 540 - 457
T ≤ 83

38. Example 2
• f/3 ≥ 4
• f/3 ▪ 3 ≥ 4 ▪ 3
• F ≥ 12
To play a board
game, there must
be at least 4 people
on each team. You
divide your friends
into 3 groups.
Write and solve an
inequality to
represent the
number of friends
playing the game.

39. Example 3:
• 0.50 x +45 ≤ 50
• 0.50 x +45 -45 ≤ 50 -45
• 0.50 x ≤ 5
• 0.50 x / 0.50 ≤ 5 /0.50
• x ≤ 10
You budget $50 a
month for your cell
phone plan. You pay
$45 for your minutes
and 250 text messages.
You are charged an
extra $0.50 for picture
messages. Write and
solve an inequality to
find the number of
picture messages you
can send without
going over your
budget.