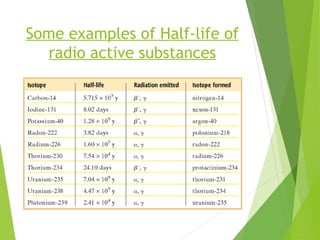
The document discusses the concept of half-life, which is defined as the time it takes for half of the nuclei in a radioactive sample to decay. Each radioactive isotope has its own characteristic half-life that can range from fractions of a second to billions of years. The number of undecayed nuclei decreases exponentially over time according to the radioactive decay equation. Examples of half-lives for some isotopes like uranium-238 and carbon-14 are provided to illustrate the range and applications of half-life.

2. HALF LIFE
Presented By
GROUP D
By: Jawad 109
Saeed 106
Saleem 079
Hanan 103
Majid 115

3. Half Life
 The half-life of a radioactive substance is
the time interval during which half of a
given number of radioactive nuclei decay
and half remains un-decay.

4. During each half-life, half of the remaining
radioactive substance decay into atoms of a new
element.
`
Where “Th” is thorium and “Pa” is protactinium.
234
90 Th 234
91
Pa + 0
-1β
HALF LIFE

5. Each radioactive nuclide has its own
half life. Half-lives can be a short as a
fraction of a second or as long as billions
of years.
Like some examples are given below:

6. Some examples of Half-life of
radio active substances

7.  One isotope of uranium that has a long
half-life is uranium-238.
 4.5 billion years
 decays through a complex series of
unstable isotopes to the stable
isotope of lead-206.

8. Decay Series of U-238
(Stable Isotope)

9. Exponential behavior of the number of
undecayed nuclei
It is given by:
where the constant N0 represents the number of
undecayed radioactive nuclei at t=0.
Equation shows that the number of undecayed radioactive
nuclei in a sample decreases exponentially with time.

10. Mathematical Expression:
The expression of decay process is given by:
N= Number of un-decay nuclie in a radioactive sample of remaining after some interval.
dN= Rate of change of un-decay nuclie
dt= Rate of change of time
Where λ is called the “decay constant”, is the probability of decay per
nucleus per second. The negative sign indicates that dN/dt is negative; that is, N
decreases in time.
This equation can be written in the form

11. Radioactive Decay
To find an expression for the half-life,
we first set
N=N0/2 and N=Noe-λt1/2
Canceling the N0 factors and then taking the reciprocal of both sides, we obtain
Taking the natural logarithm of both sides gives and finally we obtain:
…………………(1)

12. Half Life in general
 After a time interval equal to one half-life, there are
N0/2 radioactive nuclei remaining (by definition);
 After two half-lives, half of these remaining nuclei have
decayed and N0/4 radioactive nuclei are left;
 After three half-lives, N0/8 are left; and so on.
 In general, after n half-lives, the number of undecayed
radioactive nuclei remaining is (it is use to find fraction
%)
where n can be an integer n= 1, 2, 3, ….

13. Some examples of half life

14. Some examples of half life

15. Graphically
Plot of the exponential decay of radioactive nuclei. The vertical
axis represents the number of undecayed radioactive nuclei present
at any time t, and the horizontal axis is time.

16. Decay Rate
“Decay rate R is the number of decays per second.”
it can be obtained by:
where Ro=λNo is the decay rate at t=0.
The decay rate R of a sample is often referred to as its activity.
Note that both N and R decrease exponentially with time.
Another method useful in characterizing nuclear decay is the
half-life T1/2:

17. MEASURES OF RADIOACTIVITY
 A frequently used unit of activity is the curie (Ci), defined as
1 Ci = 3.7x1010
decays/s
This value was originally selected because it is the approximate
activity of 1 g of radium. The SI unit of activity is the Becquerel
(Bq):
1 Bq = 1 decay/s
Therefore,
1 Ci = 3.7x1010
Bq.
The curie is a rather large unit, and the more frequently used
activity units are the millicurie and the micro curie.

18. EXAMPLE

19. References:
 Physics for Scientists and Engineers with Modern
Physics ( 8E 2009 ISBN 978143904844 )Raymond A.
Serway, John W. Jewett

20. Thank
you