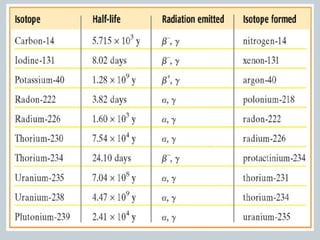
The document discusses nuclear stability and decay, highlighting that out of over 1500 known isotopes, only 264 are stable and the stability is influenced by the neutron-to-proton ratio. It explains the band of stability and the importance of neutrons in countering electrostatic repulsion among protons, with no stable isotopes existing beyond atomic number 83. Additionally, it covers half-life as the time required for half of a radioactive sample to decay, using examples like uranium-238 and phosphorus-32 to illustrate decay rates and calculations.

1. Nuclear Stability and Decay
• More than 1500 different isotopes are known. Of
those, only 264 are stable and do not decay over time.
• One factor that affects the stability of nucleus is the
ratio of neutrons to protons.
• Too many or too few neutrons relative to the number
of protons makes the nucleus unstable.
• A neutron vs proton plot of stable nuclei form a
pattern called the band of stability.

2. Band of Stability

3. • For elements with atomic numbers 20 or less, this
ratio is about 1:1. Above atomic number 20, stable
nuclei have more neutrons than protons.
• The band of stability can be explained by the
relationship between the nuclear force and the
electrostatic forces between protons.
– As the number of protons in a nucleus increases, the
repulsive electrostatic force between protons increases
faster than the nuclear force.
– More neutrons are required to increase the nuclear force
and stabilize the nucleus.
– Beyond the atomic number 83, bismuth, the
repulsive force of the protons is so great that
no stable isotopes exists.

5. Half-Life
– Every radioisotope has a characteristic rate of
decay, which is measured by its half-life.
– Half-life is the time required for one-half of the nuclei
in a radioisotope sample to decay.
– During each half-life, half of the remaining
radioactive atoms decay into atoms of a new
element.
– Each radioactive nuclide has its own half-life. Half-
lives can be a short as a fraction of a second or as
long as billions of years.

7. • One isotope that has a long half-life is uranium-238.
– 4.5 billion years
– decays through a complex series of unstable
isotopes to the stable isotope of lead-206.

8. Decay Series of U-238
Stable Isotope

9. – The following equation can be used to calculate
how much of an isotope will remain after a given
number of half-lives.
A = Ao x (1/2)n
• A stands for the amount remaining, Ao for the
initial amount, and n for the number of half-
lives.

10. Half-Life Sample Problem
Phosphorus-32 has a half-life of 14.3 days.
a) How long is four half-lives?
b) If you started with 24.0 g of phosphorus-32, how
many grams of the isotope remain at the end four
half-lives?

11. Outcome Sentences
• After reflecting on
today’s lesson,
complete three of the
sentence starters.
• Sentence Starters
– I’ve learned…
– I was surprised…
– I’m beginning to wonder…
– I would conclude…
– I now realize that…