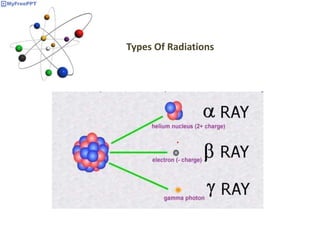
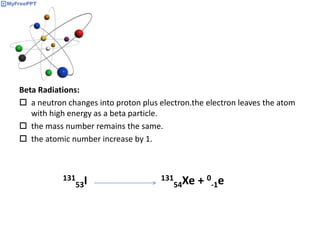
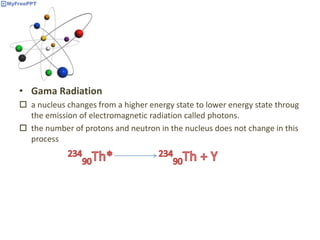
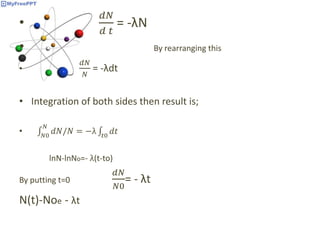
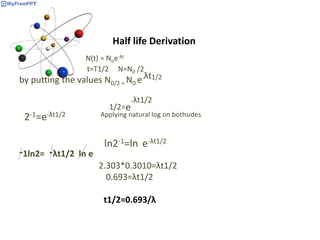
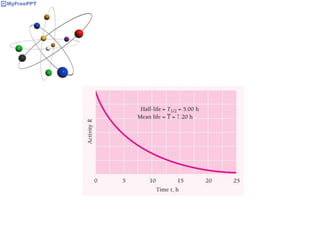
Radioactive decay occurs when the nucleus of an atom spontaneously disintegrates. Heavy atoms like uranium, thorium, radium, and polonium undergo this process, emitting alpha, beta, or gamma radiation. The rate of radioactive decay follows first-order kinetics, meaning the rate of decay is proportional to the amount of radioactive material. This allows scientists to define quantities like half-life, the time it takes for half of a radioactive sample to decay, and mean life, the average lifetime of radioactive atoms, which is equal to the half-life divided by the natural logarithm of two.

1. Radioactive
Decay
Presented by:
SABA ALI
Semester#03
Roll#43

2. Early pioneers of
Radioactivity
Roentgen Becquerel
Rutherford
Marie curie
Pierre curie
Discover
Alpha Beta
particles and
Gamma
particles.
Discovery of
Radioactive
elements.
Discovered
Radium and
Polonium in
1900-1908
Henry
Becquerel

3. Radioactive Decay
• The phenomenon in which the nucleus of the heavy
atom undergoes spontaneous and uncontrollable
disintegration.
• heavy atoms include; uranium(U), thorium( th) ,
radium(Ra) and polonium(Po)
210
84po 4
2He + 206
82pb
• after disintigration Alpha , Beta , Gamma radiations
emiits.

4. Types Of Radiations

5. Alpha radiations:
 it is actually the nucleus of helium atom consisting of 2 protons and 2
neutreons,held tightly together.
 the mass number decreases by 4
 the atomic number decreases by 2

6. Beta Radiations:
 a neutron changes into proton plus electron.the electron leaves the atom
with high energy as a beta particle.
 the mass number remains the same.
 the atomic number increase by 1.
131
53I 131
54Xe + 0
-1e

7. • Gama Radiation
 a nucleus changes from a higher energy state to lower energy state throug
the emission of electromagnetic radiation called photons.
 the number of protons and neutron in the nucleus does not change in this
process

8. Radioactivity Decay Law
• When a radioactive material undergoes α, β or γ-decay, the number of nuclei
undergoing the decay, per unit time, is proportional to the total number of
nuclei in the sample material.
•
•
• Where is a proportionality between radioactive decays per unit time and the
overall number of nuclei of radioactive compounds.

9. •
𝑑𝑁
𝑑 𝑡
= -λN
• By rearranging this
•
𝑑𝑁
𝑁
= -λdt
• Integration of both sides then result is;
• 𝑁0
𝑁
𝑑𝑁/𝑁 = −λ 𝑡0
𝑑𝑡
lnN-lnNo=- λ(t-to)
By putting t=0
𝑑𝑁
𝑁0
= - λt
N(t)-Noe - λt

11. • SI unit of Activity is Becquerel
• 1 Becquerel =1 Bq =1 decay/s
• Curie =3.7*10 radioactive decay per second

12. Half - Life
T1/2
• the time required for half the amount of a radioactive
substance to decay.
• Every radionuclide has a characteristic half-life. Some half-
lives are only a millionth of a second, others are billions of
years.

13. Half life Derivation
N(t) = Noe-λt
t=T1/2 N=N0 /2
by putting the values N0/2 = N0 e-λt1/2
1/2=e
-λt1/2
2-1=e-λt1/2 Applying natural log on bothsides
ln2-1=ln e-λt1/2
-1ln2= -λt1/2 ln e
2.303*0.3010=λt1/2
0.693=λt1/2
t1/2=0.693/λ

15. Mean life
• Mean life is the average lives of a radioactive substance.
• It is denoted by τ
τ=1/λ
Since, λ=0.693/T1/2
Hence,
τ= T1/2
0.693