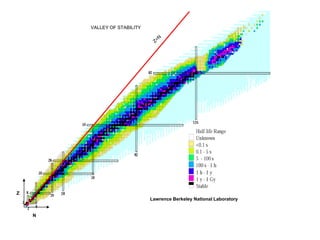
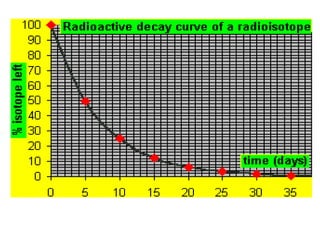
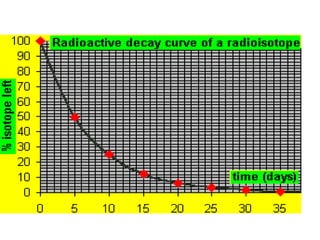
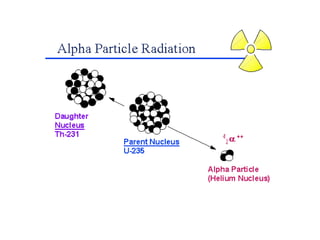
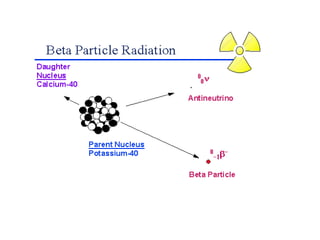
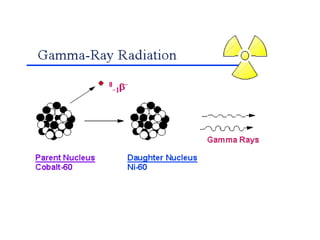
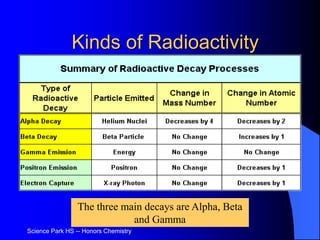
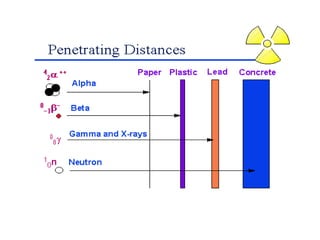
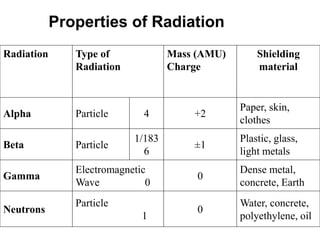
The document discusses the stability of atomic nuclei and different types of radioactive decay. It explains that nuclei are stable when the nuclear binding forces outweigh the electrostatic repulsion between protons. Unstable nuclei undergo radioactive decay through processes like alpha, beta, or gamma emission to become more stable. The activity of a radioactive sample decreases exponentially over time according to the half-life. Different modes of decay include alpha emission by nuclei with too few neutrons, beta emission changing the number of protons and neutrons, and gamma emission releasing excess energy.

1. THE STABILITY OF THE
NUCLEUS
Radioactivity

2. • radioactive decay - when a radionuclide changes
from one nuclear configuration to another
• occurs in various ways eg ejection of an alpha
particle, beta particles and gamma rays from the
nucleus.
• It would appear that the atomic nucleus is
inherently unstable - it contains both neutrons
(uncharged) and protons (positively charged) which
would electrostatically repel each other.

3. • In practice it is not so.
• The nucleus is a dynamic (and not static)
entity where two opposing forces are in
action. One force tends to disrupt the nucleus
while the other holds it together. A stable
nucleus is one where the disruptive force
never wins , for example 12
6C whereas 14
6C is
of the unstable kind.

4. • The forces that hold the nucleus together are called
short- range nuclear forces and are effective over
distances of 10-15meters.
• The energy used to keep the nucleus intact is called
the nuclear binding energy (NBE).
• For most nuclei the binding energy per nucleon is
8.4MeV and is obtained by dividing the NBE by the
number of nucleons (A) in the nucleus.
• The NBE between nucleons comes from the
transformation of part of the nuclear mass into
energy according to Einstein’s equation E = mc2.

5. • Each nucleon has a mass of about 931MeV
per atomic mass unit (amu) and about 8.4
MeV of this is used as NBE – which keeps it
bound to its neighbouring nucleons.
• Due to this fact, the mass of the nucleus is
always less than the sum of the masses of the
nucleons.

6. • An unstable nucleus releases energy to
become more stable

7. RADIOACTIVITY
• Term applied to nuclei which are
unstable
• Forces disrupting nucleus stronger than
forces holding nucleus together
• Changes internal structure to a more
stable form eg by ejecting a particle

8. Terms relating to radioactivity
• Each time a nucleus changes its internal structure
radioactive disintegration or nuclear
transformation
• may result in a change in the atomic number or a
change in the mass number or a change of both
• A decay scheme is a pictorial representation of the
decay process.
• branching scheme - a nucleus undergoes more than
one type of transformation

9. Unit of Radioactivity
• The unit of radioactivity is the Becquerel
(Bq).
• 1 Becquerel = 1 nuclear disintegration
per second.

10. Nuclide chart
• Plot of no of neutrons against no. of protons
• For lighter elements nuclear stability produced
when protons=neutrons
• As Z increases more neutrons required -to
produce short range nuclear forces
• Z >83 not possible to produce stable nuclear
configuration

11. All the elements heavier than Bismuth (At # 83)

12. Their atoms emit 3 things…alpha,
beta particles and gamma rays

13. N
Z
Lawrence Berkeley National Laboratory
VALLEY OF STABILITY

15. Radioactivity & exponential decay
• The older a sample of a radioactive material, the
less radioactive it is.
• The decrease in radioactivity follows a
characteristic pattern shown in the graph or decay
curve.
• After every half-life, (in this case 5 days, working
out from the graph), the % radioisotope (or
radioactivity) is halved, producing the initially
steeply declining curve which then levels out
towards zero at infinite time!

16. Radioactivity & exponential law
• A plot of activity against time gives the above curve.
• initial fall in the number of atoms is steep but slows down
as less and less of the original nuclei are left. The number
of original nuclei never reaches zero.
• Equation for the curve is expressed as
At = A0 e-λt
where At is the activity after time t, A0 is the initial activity, e is
the exponential constant, λ is the decay constant and t is
the time after the initial measurement.

17. Terms & definitions
• Activity At of a radioactive substance at time t is defined
as the product of the decay constant λ and the number
of radioactive nuclei N(t)
• Аt = λN(t)
• The simplest radioactive decay is characterised by a
radioactive parent nucleus P decaying with a decay
constant λp into a stable daughter nucleus D
λp
P D
•

18. Radioactive Decay
• A more complicated radioactive decay occurs
when a radioactive parent nucleus P decays
with a decay constant λp into a daughter
nucleus D which in turn is radioactive and
decays with a decay constant λD into a stable
granddaughter G

19. Radioactive Decay and The
Exponential Law
Definition of exponential law
• A quantity y is said to vary exponentially with x if
equal changes in x produce equal fractional (or %
) changes in y.
• Definition: law of radioactive decay states that
the rate of decay of a particular nuclide (i.e. the
number of nuclei decaying per second) is
proportional to the number of such nuclei
remaining in the sample (i.e. it is a fixed fraction
of the number of nuclei left in the in the sample).

20. • Measures of radioactivity
• Exponential decay of number of atoms of a particular
radionuclide
• It is difficult to measure the number of nuclei
remaining in practice. What can be more easily
measured is the effects of nuclear disintegrations by
counting the number of e.g. γ rays emitted using a
suitable detector to make an estimate of the total
number of disintegration per second occurring within
the radioactive. This quantity is known as the activity
of the sample measured in becquerels.

21. • Equation for the curve is expressed as
At = A0 e-λt
where At is the activity after time t, A0 is the
initial activity, e is the exponential constant, λ
is the decay constant and t is the time after
the initial measurement.

22. Some definitions and equations in
radioactivity
• The activity At of a radioactive substance at time t is
defined as the product of the decay constant λ and the
number of radioactive nuclei N(t)
А(t) = λN(t)
• The simplest radioactive decay is characterised by a
radioactive parent nucleus P decaying with a decay
constant λp into a stable daughter nucleus D
• λp
• P D

23. • The number of radioactive parent nuclei Np(t) as a function
of time t is governed by the following relationship:
Np(t) = Np (0) e –λpt
• where Np(0) is the initial number of parent nuclei at
time t=0
similarly , the activity of parent nuclei Ap(t) at time t is
given as
• Ap(t) =Ap (0) e –λpt
•
• where Ap(0) is the initial number of parent nuclei at time
t=0

24. Half life
• The half life t1/2 of a radioactive substance is the
time during which the number of radioactive
nuclei decays to half of the initial value Np(0)
present at time t = 0
Np (t=t1/2) = (1/
2 ) Np (0) = Np(0)e-λpt
1/2
• The decay constant λp and the half life (t1/2) for
the parent have the following relationship
Ap =loge2
t1/2

26. Half Life
• The half life t1/2 of a radioactive substance is the
time during which the number of radioactive
nuclei decays to half of the initial value Np(0)
present at time t = 0
• Np (t = t1/2) = (1/
2 ) Np (0) = Np(0)e-λpt
1/2
• The decay constant λp and the half life (t1/2) for the
parent have the following relationship
• Ap =loge2t1/2

27. Physical, biological & effective half life
• Biological – time taken for the concentration of a
certain chemical to reduce to half its original
concentrationdue solely to biological elimination –
affected by body’s ability to excrete the chemical
• Physical half-life is defined as the period of time
required to reduce the radioactivity level of a
source to exactly one half its original value due
solely to radioactive decay.
• Effective – activity of radionuclide to reduce to
half its original -affected by physical and
biological half lives
• 1/t1/2(eff) =1/ t1/2(phy) + 1/ t1/2(bio)

28. Calculation
• An isotope of I –131 has a half life of 8
days. 16.8 MBq is required for a study
starting at 10:00 on 19 March. If this
isotope is to be dispensed at 10:00 on
March 3, what activity should be
dispensed?

29. Exercise
• Assuming that the biological half life of iodine
131 (131I) is 21 days, calculate the effective half
life of iodine. The physical half life of iodine is
8 days.

30. Radioactivity
Modes of Radioactive decay

31. Radioactive Decay

32. Alpha Particle Emission
• Z >150
• Too few neutrons for no. of protons – higher
neutron to proton ratio required to produce
nuclear stability
• Alpha particle – 2 protons & 2 neutrons
(helium nucleus)

34. Beta particle emission
• Particle ejected has mass equal to that of
electron
• Can have either a positive or negative charge –
negatron or positron
• Negatron emission
n p + negatron
• Positron emission
• p n + positron

36. Gamma Ray Decay
• Emitted from nucleus with excess energy
• Daughter nucleus left in excited state
• Excited state lasting sufficiently long for the
duration to be measured – metastable state
• Transition from metastable state to more
stable state – isomeric transition

38. Internal Conversion
• Competes with gamma decay
• Process -result of the direct interaction
between the nucleus and an orbiting electron
so that the nucleus drops to its ground state
by giving all its excess energy to the electron.
• Converted electron escapes from the atom
with an energy equal to that donated by the
nucleus minus the binding energy of that
particular electron

39. Electron Capture
• If a nucleus of low mass number has too few
neutrons for stability but has insufficient excess
energy to eject a positron, then as an alternative
way the nucleus may undergo an isobaric
transformation and loose energy by electron
capture.
• Nucleus captures one of the orbiting electrons
• Process involves the conversion of a proton to a
neutron.

40. Fission
• Forces holding nucleus together become
increasingly important as the size of the
nucleus increases.
• A very large nucleus can be visualised as
being like a liquid drop in which the nucleons
are moving about with very high energy and
continuously deforming the shape of the
nucleus.

41. FISSION
• During this process the nucleus can become
very elongated and break into two
fragments- usually of fairly similar sizes.
• This is spontaneous fission and can occur
for very large nuclei e.g. thorium – 232.
• In addition to the fission fragments from
such a reaction, one or more neutrons are
usually liberated and the whole process is
accompanied by the release of large
amounts of energy.

42. Z
N
A
Z
N
A-4
Z-2
N-2
A
Z-1
N+1
A
Z+1
N-1
b+
E.C.
b-
Various decay modes
Negative beta decay n = p + e- + v + E
Positron decay p = n + e+ + v + E
Alpha decay A
ZX = A-4
Z-2X + 4
2He + E
Electron capture p + e- = n + E
Fission decay (break down to subequal atoms)

43. Science Park HS -- Honors Chemistry
Kinds of Radioactivity
The three main decays are Alpha, Beta
and Gamma

45. Properties of Radiation
Radiation Type of
Radiation
Mass (AMU)
Charge
Shielding
material
Alpha Particle 4 +2
Paper, skin,
clothes
Beta Particle
1/183
6
±1
Plastic, glass,
light metals
Gamma
Electromagnetic
Wave 0
0
Dense metal,
concrete, Earth
Neutrons
Particle
1
0
Water, concrete,
polyethylene, oil

46. Science Park HS -- Honors Chemistry
Early Pioneers in Radioactivity
Roentgen:
Discoverer of
X-rays 1895
Becquerel:
Discoverer of
Radioactivity
1896
The Curies:
Discoverers of
Radium and
Polonium 1900-
1908
Rutherford:
Discoverer
Alpha and Beta
rays 1897