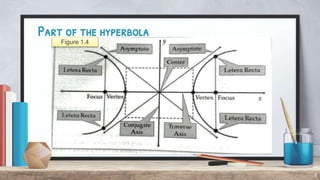
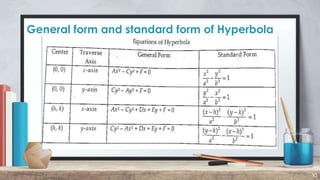
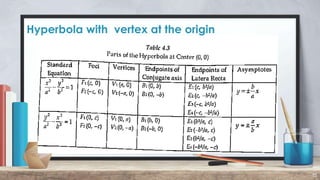
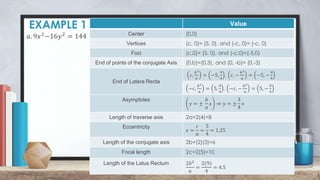
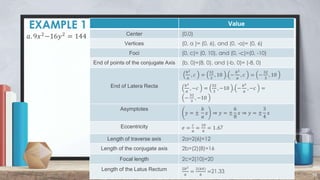
The document defines and provides examples of converting general hyperbola equations to standard form. A hyperbola is defined as the set of all points where the difference between the distances from two fixed points (foci) is a constant. Examples show converting equations to standard form by completing the square and identifying the center, vertices, foci, and axes. Standard form is x^2/a^2 - y^2/b^2 = 1, where a and b are the distances to the vertices and conjugate axis endpoints from the center.

1. Hyperbola
1

2. 2
hyperbola
when the plane (not necessarily
vertical) intersects both cones to form
two unbounded curves (each called a
branch of the hyperbola)

3. hyperbola
3
is a set of all points in a place such the difference
of the distances of each point of the set from the fixed
points is constant. The fixed point are called foci.
Since c>a, the number 𝒄𝟐
− 𝒂𝟐
is a positive; we let 𝒃𝟐
= 𝒄𝟐
−
𝒂𝟐
. Then we can write the equation of the Ellipse
𝑥2
𝑎2
−
𝑦2
𝑏2
= 1

4. hyperbola
4
Figure 1.1

5. Part of the hyperbola
5
Horizontal Hyperbola
Figure 1.3
𝑥2
𝑎2
−
𝑦2
𝑏2
= 1
𝑦2
𝑎2
−
𝑥2
𝑏2
= 1
Vertical Hyperbola
Figure 1.2

6. Definition of terms:
6
Focus- is called eccentricity of the hyperbola.
Vertices- the points of the hyperbola with the traverse axis.
Directrix (fixed line)- is a line such that the ratio of distance
of the points on the hyperbola from the focus to its
distance from the directrix is constant.
Latera Recta- the line segment passing through the foci
and perpendicular to the transverse axis.
Transverse axis- the line segment joining the vertices.
Conjugate axis- the segment which is perpendicular
bisector of the transverse axis with the length of 2b.

7. Definition of terms:
7
Focal length- is the line segment joining the foci with the
length of 2c.
Asymptote- the lines that pass to the center of the
hyperbola and are asymptotic to the curves.
Center- is the center where the two asymptotes intersect,
or it can be defined as the intersection of the traverse and
conjugate.

8. Part of the hyperbola
8
Figure 1.4

9. For simplicity, the following will be represented as;
9
𝑪= Center of the Hyperbola
𝑭𝟏, 𝑭𝟐 = Foci(Plural form of
focus)
𝑽𝟏, 𝑽𝟐= Vertices
𝑩𝟏, 𝑩𝟐 =Endpoint of the
conjugate axis
𝑷 𝒙, 𝒚 = any point along the
Hyperbola
𝑫𝟏, 𝑫𝟐= Directrices
𝑬𝟏, 𝑬𝟐, 𝑬𝟑, 𝑬𝟒= Endpoints of the
Latera Recta
𝒂= distance from the center to
vertex
𝒃= distance from the center to
one endpoint of the conjugate
axis.
𝒄= distance from the center to
Focus.
𝒆= eccentricity
𝟐a= length of the transverse axis
𝟐𝒃= length of the conjugate axis
2c= focal length

10. General form and standard form of Hyperbola
10

11. EXAMPLE 1
11
Convert the following general equations to standard form:
a. 3𝑥2 − 2𝑦2 = 12
b. 9𝑦2−16𝑥2 = 144
𝑎. 3𝑥2
− 2𝑦2
= 12
3𝑥2
12
−
2𝑦2
12
=
12
12
𝑥2
4
−
𝑦2
6
= 1
𝑏. 9𝑦2−16𝑥2 = 144
9𝑦2
144
−
16𝑦2
144
=
144
144
𝑥2
16
−
𝑦2
9
= 1

12. EXAMPLE 2
12
Convert the following general equations to standard form:
a. 𝑦2 − 5𝑥2 + 30𝑥 + 4𝑦 − 46 = 0
b. 9𝑥2−4𝑦2 + 18𝑥 − 16𝑦 − 43 =0
𝑎. )𝑦2
− 5𝑥2
+ 30𝑥 + 4𝑦 − 46 = 0
(𝑦 + 2)2
5
−
5(𝑥 − 3)2
5
=
5
5
(𝑦2
+ 4𝑦) − 5 𝑥2
− 6𝑥 = 46
(𝑦2
+ 4𝑦 + 4) − 5 𝑥2
− 6𝑥 + 9 = 46 + 4 + −5 (9)
(𝑦2
+ 4𝑦 + 4) − 5 𝑥2
− 6𝑥 + 9 = 46 + 4 − 45
(𝑦2
+ 4𝑦 + 4) − 5 𝑥2
− 6𝑥 + 9 = 5 (𝑦 + 2)2
5
−
(𝑥 − 3)2
1
= 1

13. EXAMPLE 3
13
Convert the following general equations to standard form:
9(𝑥 + 1)2
36
−
4 𝑦 + 2 2
36
=
36
36
𝑏. 9𝑥2
−4𝑦2
+ 18𝑥 − 16𝑦 − 43 = 0
(9𝑥2 + 18𝑥) + −4𝑦2 − 16𝑦 = 43
9 𝑥2 + 2𝑥 − 4 𝑦2 + 4𝑦 = 43
9 𝑥2 + 2𝑥 + 1 − 4 𝑦2 + 4𝑦 + 4 = 43 + (9_ 1 + (−4)(4)
9(𝑥 + 1)2−4 𝑦 + 2 2 = 43 + (9) 1 + (−4)(4)
9(𝑥 + 1)2−4 𝑦 + 2 2 = 43 + 9 1 − 16
(𝑥 + 1)2
4
−
4 𝑦 + 2 2
9
= 1

14. EXAMPLE 4
14
Convert the following general equations to standard form:
9(𝑥 + 1)2
36
−
4 𝑦 + 2 2
36
=
36
36
𝑏. 9𝑥2
−4𝑦2
+ 18𝑥 − 16𝑦 − 43 = 0
(9𝑥2 + 18𝑥) + −4𝑦2 − 16𝑦 = 43
9 𝑥2 + 2𝑥 − 4 𝑦2 + 4𝑦 = 43
9 𝑥2 + 2𝑥 + 1 − 4 𝑦2 + 4𝑦 + 4 = 43 + (9_ 1 + (−4)(4)
9(𝑥 + 1)2−4 𝑦 + 2 2 = 43 + (9) 1 + (−4)(4)
9(𝑥 + 1)2−4 𝑦 + 2 2 = 43 + 9 1 − 16
(𝑥 + 1)2
4
−
𝑦 + 2 2
9
= 1

15. Hyperbola with vertex at the origin
15

16. EXAMPLE 1
16
Convert the following general equations to standard form:
𝑎. 9𝑥2−16𝑦2 = 144
𝑏. 64𝑥2
−36𝑦2
= 2304
𝑎. 9𝑥2−16𝑦2 = 144
9𝑦2
144
−
16𝑦2
144
=
144
144
𝑥2
16
−
𝑦2
9
= 1
Since 𝑥2
is positive the traverse
axis is parallel with x-axis.
𝑎2
= 16 → 𝑎 = 4
𝑏2 = 9 → 𝑏 = 3
𝑐2
= 𝑎2
+ 𝑏2
𝑐2 = 16 + 9
𝑐2 = 25 → 𝑐 = 5

17. EXAMPLE 1
17
Value
Center (0,0)
Vertices (c, 0)= (5, 0), and (-c, 0)= (-c, 0)
Foci (c,0)= (5, 0), and (-c,0)=(-5,0)
End of points of the conjugate Axis (0,b)=(0,3), and (0, -b)= (0,-3)
End of Latera Recta
𝑐,
𝑏2
𝑎
= −5,
9
4
, 𝑐, −
𝑏2
𝑎
= −5, −
9
4
−𝑐,
𝑏2
𝑎
= 5,
9
4
, −𝑐, −
𝑏2
𝑎
= 5, −
9
4
Asymptotes
𝑦 = ±
𝑏
𝑎
𝑥 ⇒ 𝑦 = ±
3
4
𝑥
Length of traverse axis 2a=2(4)=8
Eccentricity
𝑒 =
𝑐
𝑎
=
5
4
= 1.25
Length of the conjugate axis 2b=(2)(3)=6
Focal length 2c=2(5)=10
Length of the Latus Rectum 2𝑏2
𝑎
=
2(9)
4
= 4.5
𝑎. 9𝑥2
−16𝑦2
= 144

18. EXAMPLE 2
18
Convert the following general equations to standard form:
𝑏. 64𝑦2
−36𝑦2
= 2304
64𝑦2
2304
−
36𝑥2
2304
=
2304
2304
𝑦2
36
−
𝑥2
64
= 1
Since 𝑥2
is positive the traverse
axis is parallel with x-axis.
𝑎2
= 36 → 𝑎 =6
𝑏2 = 64 → 𝑏 = 8
𝑐2
= 𝑎2
+ 𝑏2
𝑐2 = 36 + 64
𝑐2 = 100 → 𝑐 = 10

19. EXAMPLE 1
19
Value
Center (0,0)
Vertices (0, a )= (0, 6), and (0, -a)= (0, 6)
Foci (0, c)= (0, 10), and (0, -c)=(0, -10)
End of points of the conjugate Axis (b, 0)=(8, 0), and (-b, 0)= (-8, 0)
End of Latera Recta
𝑏2
𝑎
, 𝑐 =
32
3
, 10 , −
𝑏2
𝑎
, 𝑐 = −
32
3
, 10
𝑏2
𝑎
, −𝑐 =
32
3
, −10 , −
𝑏2
𝑎
, −𝑐 =
−
32
3
, −10
Asymptotes
𝑦 = ±
𝑏
𝑎
𝑥 ⇒ 𝑦 = ±
6
8
𝑥 ⇒ 𝑦 = ±
3
4
𝑥
Eccentricity 𝑒 =
𝑐
𝑎
=
10
6
= 1.67
Length of traverse axis 2a=2(6)=12
Length of the conjugate axis 2b=(2)(8)=16
Focal length 2c=2(10)=20
Length of the Latus Rectum 2𝑏2
𝑎
=
2(64)
6
=21.33
𝑎. 9𝑥2
−16𝑦2
= 144

20. Hyperbola with vertex at (h,k)
20

21. EXAMPLE 1
21
Convert the following general equations to standard form:
𝑎. 9𝑥2
−16𝑦2
− 18𝑥 + 64𝑦 − 199 = 0
9(𝑥 − 1)2
144
−
16(𝑦 − 2)2
144
=
144
144
9(𝑥2−2𝑥) − 16(𝑦2 − 4𝑦) = 199
9(𝑥2−2𝑥) − 16(𝑦2 − 4𝑦) = 199 + 9(1) + (−16)(4)
9(𝑥2−2𝑥 + 1) − 16(𝑦2 − 4𝑦 + 4) = 199 + 9(1) + (−16)(4)
(𝑥 − 1)2
16
−
𝑦 − 2 2
9
= 1

22. EXAMPLE 1
22
Convert the following general equations to standard form:
𝑎. 9𝑥2
−16𝑦2
− 18𝑥 + 64 − 199 = 0
Since 𝑥2
is positive the traverse axis is parallel with x-axis.
𝑎2
= 16 → 𝑎 = 4
𝑏2 = 9 → 𝑏 = 3
𝑐2
= 𝑎2
+ 𝑏2
𝑐2 = 16 + 9
𝑐2
= 25 → 𝑐 = 5

23. EXAMPLE 1
23
Center C=(h, k)= (1, 2)
Vertices
𝑉1 = ℎ + 𝑎, 𝑘 = (1 + 4, 2) = 5, 2
𝑉2 = ℎ − 𝑎, 𝑘 = (1 − 4, 2) = (−3, 2)
Foci
𝐹1 = ℎ + 𝑐, 𝑘 = (1 + 5, 2) = 6, 2
𝐹2 = ℎ − 𝑐, 𝑘 = (1 − 5, 2) = (−4, 2)
End of points of the
conjugate Axis
𝐵1 = ℎ, 𝑘 + 𝑐 = (1, 2 + 3) = 1, 5
𝐵2 = ℎ, 𝑘 − 𝑐 = 1, 2 − 3) = (1, −1)
End of Latera Recta
𝐸1 = ℎ + 𝑐, 𝑘 +
𝑏2
𝑎
= 1 + 5, 2 +
9
4
= (6, 4.25)
𝐸2 = ℎ + 𝑐, 𝑘 −
𝑏2
𝑎
= 1 + 5, 2 −
9
4
= (6, −0.25)
𝐸3 = ℎ − 𝑐, 𝑘 +
𝑏2
𝑎
= 1 − 5, 2 +
9
4
= (−4, 4.25)
𝐸4 = ℎ − 𝑐, 𝑘 −
𝑏2
𝑎
= 1 − 5, 2 −
9
4
= (−4, −0.25)
𝒂. 𝟗𝒙𝟐
−𝟏𝟔𝒚𝟐
− 𝟏𝟖𝒙 + 𝟔𝟒 − 𝟏𝟗𝟗 = 𝟎

24. EXAMPLE 1
24
𝒂. 𝟗𝒙𝟐
−𝟏𝟔𝒚𝟐
− 𝟏𝟖𝒙 + 𝟔𝟒 − 𝟏𝟗𝟗 = 𝟎
Asymptotes
𝑦 − 𝑘 = ±
𝑏
𝑎
(𝑥 − ℎ) ⇒ 𝑦 − 2 = ±
3
4
(𝑥 − 1)
3x-4y+5=0, and 3x+4y-11=0
Eccentricity 𝑒 =
𝑐
𝑎
=
5
4
= 1.25
Length of transverse axis 2a=2(4)=8
Length of the conjugate axis 2b=(2)(3)=6
Focal length 2c=2(5)=10
Length of the Latus Rectum 2𝑏2
𝑎
=
2(9)
6
=4.5

25. GENERALIZATION
25

26. 26
EVALUATION

27. Exercises
27
Convert the general form to standard form then find the center,
vertices, foci, endpoints of the conjugate axis, endpoints of the latera recta,
Asymptote, eccentricity, length of transverse axis, length of the conjugate
axis, and length of the latus rectum.
1. 9𝑦2
−25𝑥2
+ 200𝑥 − 54𝑦 − 544 = 0

28. 28
ASSIGNMENT