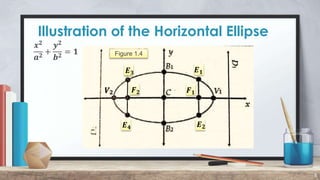
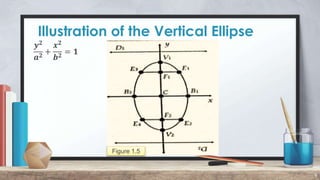
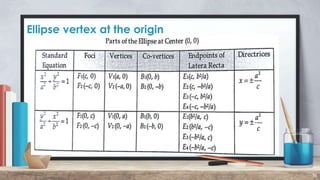
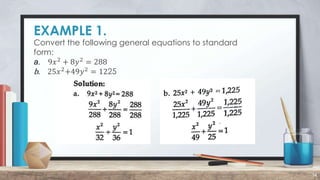
1. The document defines an ellipse as a set of points in a plane where the sum of the distances from two fixed points (foci) is a constant. 2. It provides properties of ellipses including that the length of the major axis is 2a, the minor axis is 2b, and the eccentricity e is the ratio of the distance between foci to the distance between vertices. 3. Examples are given of converting equations to standard form and finding the vertices, foci, axes lengths, and other ellipse properties. Generalizations and exercises related to analyzing ellipse equations are also presented.

1. ELLIPSE
1

2. 2
ELLIPSE
when the (tilted) plane intersects only
one cone to form a bounded curve

3. ELLIPSE
3
An ellipse is a set of all points in a plane the sum
whose distances from two fixed points 𝒇𝟏 and 𝒇𝟐 is a
constant number.
• 𝒇𝟏and 𝒇𝟐 are the two fixed point called foci.

4. ELLIPSE
4
Let say, if 𝐹1 and 𝐹2
are two fixed point and 𝑘 is
positive constant as shown
in Figure 1.1 then the ellipse
determined by 𝐹1, 𝐹2 and 𝑘 is
the set of points 𝑃(𝑥, 𝑦) such
that 𝑃𝐹1 + 𝑃𝐹2 = 𝑘.
Standard Equation of Ellipse:
𝑥2
𝑎2
+
𝑦2
𝑏2
= 1
Figure 1.1

5. Definition of terms:
5
Ratio- is called eccentricity of the ellipse.
Center- is the intersection of the major axis and the minor
axis.
Axis of symmetry- line passes to the through both foci.
Vertices- meets at two points.
Major axis (traverse axis)- the line joining the vertices and
foci and has a length of 2a.
Semi-major axis- the number a of the ellipse.
Minor axis (conjugate axis)- the line segment which is a
perpendicular bisector of the major axis.

6. Definition of terms:
6
Directrix- is a line such that
ratio of distance of the points
on the conic section from
focus to its distance from the
directrix is constant.
Latus rectum(Latera recta)- is
the chord that passes through
the focus and is
perpendicular to the major
axis and has both endpoints
on the curve.

7. DEFINITION
7
The ellipse can also be defined as the locus of point whose distance
from the focus is proportional to the horizontal distance from the
directrix, where the ratio is less than 1. this can be Illustrated as shown
in figure 1.2 where the ratio between the distance between
𝑃𝐹1𝑎𝑛𝑑 𝑃𝐷 are less than 1.
Figure 1.2 Figure 1.3

8. Illustration of the Horizontal Ellipse
8
𝒙𝟐
𝒂𝟐
+
𝒚𝟐
𝒃𝟐
= 𝟏 Figure 1.4
𝑽𝟐 𝑭𝟐 𝑭𝟏
𝑬𝟑 𝑬𝟏
𝑬𝟐
𝑬𝟒

9. Illustration of the Vertical Ellipse
9
𝒚𝟐
𝒂𝟐
+
𝒙𝟐
𝒃𝟐
= 𝟏
Figure 1.5

10. For simplicity, the following will be represented as;
10
𝑪= Center of the Ellipse
𝑭𝟏, 𝑭𝟐 = Foci(Plural form of
focus)
𝑽𝟏, 𝑽𝟐= Vertices
𝑩𝟏, 𝑩𝟐=Co-Vertices (endpoints
of the minor axis)
𝑷 𝒙, 𝒚 = any point along the
Ellipse
𝑫𝟏, 𝑫𝟐= Directrices
𝑬𝟏, 𝑬𝟐, 𝑬𝟑, 𝑬𝟒= Endpoints of the
Latera Recta
𝒂= distance from the center
to vertex
𝒃= distance from the center
to one endpoint of the minor
axis.
𝒄 = distance from the
center to Focus.
𝒆= eccentricity
𝟐a= length of the major axis
𝟐𝒃= length of the minor axis

11. Properties of the Ellipse
11
1. The length of the major
axis is 2a.
2. The length of the minor
axis is 2b.
3. The length of the Latus
Rectum is
𝑏2
𝑎
.
4. The center is the
intersection of the axes.
5. The endpoints of the major
axis are called the
vertices.
6. The endpoints of the minor
axis are called the co-
vertices.
7. The line segment joining the
vertices is called the major
axis.
8. The line segment joining the
co-vertices is called the minor
axis.
9. The eccentricity of the
ellipse is 0 < 𝑒 < 1.

12. THEOREM:
12
Theorem 3.1: If in the general equation of an ellipse
𝐴𝑥2
+ 𝐶𝑥2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0 and 𝑐 > 0, then the graph is
ellipse, a point, or the empty set.
Theorem 3.2: The eccentricity e of an ellipse is the ration of
the undirected distance between the foci to the undirected
distance between vertices; that is 𝑒 =
𝑐
𝑎
.

13. General form and standard form of Ellipse
13

14. EXAMPLE 1.
14
Convert the following general equations to standard
form:
a. 9𝑥2
+ 8𝑦2
= 288
b. 25𝑥2
+49𝑦2
= 1225

15. EXAMPLE 1.
15
Convert the following general equations to standard form:
a. 3𝑥2
+ 4𝑦2
+ 24𝑥 − 16𝑦 + 52 =0
b. 25𝑥2
+16𝑦2
+ 150𝑥 − 128𝑦 − 1,119 =0

16. Ellipse vertex at the origin
16

17. Graphing the Equation of the Ellipse
17

18. EXAMPLE 1.
18
Convert the equation to standard form 4𝑥2
+ 9𝑦2
= 144
4𝑥2
+ 9𝑦2
= 144
1
144
4𝑥2
+ 9𝑦2
= 144
4𝑥2
144
+
9𝑦2
144
=
144
144
𝑥2
36
+
𝑦2
16
= 1
NOTE: Since the denominator of 𝑥2
is
higher than 𝑦2
, the major axis is x-axis.
a= 36 ≈6, and
b= 16 ≈4
𝑆𝑜𝑙𝑣𝑒 𝑓𝑜𝑟 𝑐2
= 𝑎2
− 𝑏2
𝑎2
= 36, 𝑎𝑛𝑑 𝑏2
= 16
𝑐2
= 36 − 16 = 20 ⇒ 20 ≈ 4.47

19. EXAMPLE 1
19
4𝑥2
+ 9𝑦2
= 144
Value
Vertices (a, 0)= (6, 0) and (-a, 0)=(-6,0)
Co-vertices (0,b)= (0, 4) and (0,-b)= (0,-4)
Foci (c,0)= (4.47,0) and (-c,0)= (-4.47, 0)
End of points Latera Recta
𝑐,
𝑏2
𝑎
= 4.47, 2.67 , 𝑐, −
𝑏2
𝑎
= 4.47, −2.67
−𝑐,
𝑏2
𝑎
= (−4.47, 2.67), −𝑐, −
𝑏2
𝑎
= (−4.47, −2.67)
Directrices
𝑥 = ±
𝑎2
𝑐
⇒
36
20
≈ ±8.05
Eccentricity
𝑒 =
𝑐
𝑎
=
20
36
= 0.75
End of the Latus Rectum 2𝑏2
𝑎
=
2(4)2
6
=
2(16)
6
=
16
3
= 5.33
Length of the major axis 2𝑎 = 2 6 = 12
Length of the minor axis 2𝑏 = 2 4 =8

20. EXAMPLE 1
20
4𝑥2
+ 9𝑦2
= 144

21. EXAMPLE 2
21
Find the equation of the ellipse with center at (0,0) length of the major axis is 10,
and a focus at (4,0). Identify the parts of the ellipse and sketch the graph.
Second focus: (-4,0), the major axis is
the x-axis .
𝑥2
𝑎2 +
𝑦2
𝑏2 = 1, 𝑤ℎ𝑒𝑟𝑒 𝑏2
= 𝑎2
- 𝑐2
, a > 𝑏
Length of the major axis is 2a=10
a= 25 ≈5, and
c= 16 ≈4
𝑆𝑜𝑙𝑣𝑒 𝑓𝑜𝑟 𝑏2
= 𝑎2
− 𝑐2
𝑏2
= 25 − 16 = 9 ⇒ 9 ≈ 3

22. EXAMPLE 1
22
Value
Vertices (a, 0)= (5, 0) and (-a, 0)=(-5,0)
Co-vertices (0,b)= (0, 3) and (0,-b)= (0,-3)
Foci (c,0)= (4,0) and (-c,0)= (-4, 0)
End of points Latera Recta
𝑐,
𝑏2
𝑎
= 4, 1.8 , 𝑐, −
𝑏2
𝑎
= 4, −1.8
−𝑐,
𝑏2
𝑎
= (−4, 1.8), −𝑐, −
𝑏2
𝑎
= (−4, −1.8)
Directrices
𝑥 = ±
𝑎2
𝑐
⇒
25
4
≈ ±6.25
Eccentricity 𝑒 =
𝑐
𝑎
=
4
5
= 0.8
End of the Latus Rectum 2𝑏2
𝑎
=
2(3)2
5
=
2(9)
5
=
18
5
= 3.6
Length of the major axis 2𝑎 = 2 5 = 10
Length of the minor axis 2𝑏 = 2 3 =6

23. EXAMPLE 1
23

24. Ellipse with vertex at (h, k)
24

25. EXAMPLE 3
25
Convert the general form 36𝑥2
+100𝑦2
− 72𝑥 + 200𝑦 − 3,464 =0 to standard
form then find the vertices, co-vertices, foci, endpoints of the latera recta,
directrices, eccentricity, length of latus rectum, length of the major axis,
and length of the minor-axis
Solution:

26. EXAMPLE 3
26
Convert the general form 36𝑥2
+100𝑦2
− 72𝑥 + 200𝑦 − 3,464 =0 to standard form then
find the center, vertices, co-vertices, foci, endpoints of the latera recta, directrices,
eccentricity, length of latus rectum, length of the major axis, and length of the minor-
axis
(𝑥−1)2
100
+
(𝑦+1)2
36
, 𝑡ℎ𝑒 𝑑𝑒𝑛𝑜𝑚𝑖𝑛𝑎𝑡𝑜𝑟 𝑥2
is
greater than 𝑦2
the major axis is the x-
axis .
𝑥2
𝑎2 +
𝑦2
𝑏2 = 1, 𝑤ℎ𝑒𝑟𝑒 𝑐2
= 𝑎2
- 𝑏2
, a > 𝑏
a= 100 ≈ 10, and
b= 36 ≈ 6
𝑆𝑜𝑙𝑣𝑒 𝑓𝑜𝑟 𝑐2
= 𝑎2
− 𝑏2
𝑎2
= 100 𝑎𝑛𝑑 𝑐2
= 36
𝑐2
= 100 − 36 = 64 ⇒ 64 ≈8

27. EXAMPLE 3
27
Value
Center 𝑐 = ℎ, 𝑘 = (1, −1)
Vertices
𝑉1 = ℎ + 𝑎, 𝑘 = 1 + 10, , −1 = (11, −1)
𝑉2 = ℎ − 𝑎, 𝑘 = 1 − 10, , −1 = (−9, −1)
Co-Vertices
𝐵1 = ℎ, 𝑘 + 𝑏 = 1, −1 + 6 = (1, 5)
𝐵2 = ℎ, 𝑘 − 𝑏 = 1, −1 − 6 = (1, −7)
Foci
𝐹1 = ℎ + 𝑐, 𝑘 = 1 + 8, −1 = (9, −1)
𝐹2 = ℎ − 𝑐, 𝑘 = 1 − 8, , −1 = (−7, −1)
Endpoints of latera recta
𝐸1 = ℎ + 𝑐, 𝑘 +
𝑏2
𝑎
= 1 + 8, −1 + 3.6 = (9, 2.6)
𝐸2 = ℎ + 𝑐, 𝑘 −
𝑏2
𝑎
= 1 + 8, −1 − 3.6 = (9, −4.6)
𝐸3 = ℎ − 𝑐, 𝑘 +
𝑏2
𝑎
= 1 − 8, −1 + 3.6 = (−7, 2.6)
𝐸4 = ℎ − 𝑐, 𝑘 −
𝑏2
𝑎
= 1 − 8, −1 − 3.6 = (−7, −4.6)

28. EXAMPLE 3
28
Value
Directrices
𝑥 = ℎ +
𝑎2
𝑐
⇒ 1 +
100
8
= 1 + 12.25 ≈ 13.25
𝑥 = ℎ −
𝑎2
𝑐
⇒ 1 −
100
8
= 1 − 12.25 ≈ 11.25
Eccentricity 𝑒 =
𝑐
𝑎
=
8
10
= 0.8
Length of the latus Rectum
2𝑏2
𝑎
=
(2)(36)
10
= 7.2
Length of the Major Axis 2𝑎 = 2 10 = 20
Length of the minor Axis 2𝑏 = 2 6 = 12

29. EXAMPLE 3
29

30. GENERALIZATION
30

31. 31
EVALUATION

32. Exercises
32
A. Convert the general form to standard form then find the vertices, co-
vertices, foci, endpoints of the latera recta, directrices, eccentricity,
length of latus rectum, length of the major axis, and length of the minor-
axis
1. 16𝑥2
+ 25𝑦2
= 400
B. Convert the general form to standard form then find the center, vertices,
co-vertices, foci, endpoints of the latera recta, directrices, eccentricity,
length of latus rectum, length of the major axis, and length of the minor-axis
1. 25𝑥2
+9𝑦2
− 150𝑥 − 36𝑦 + 36 = 0