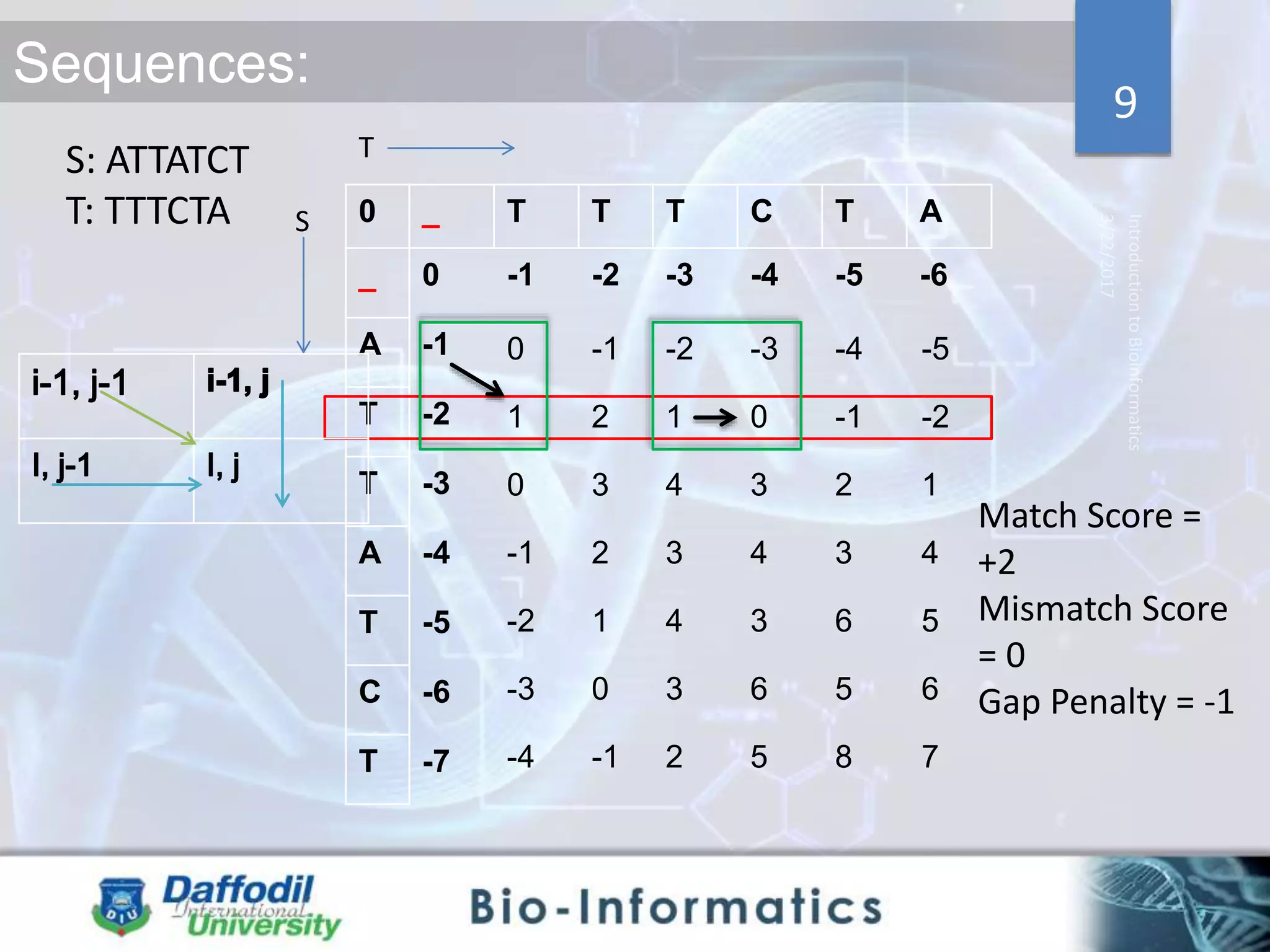
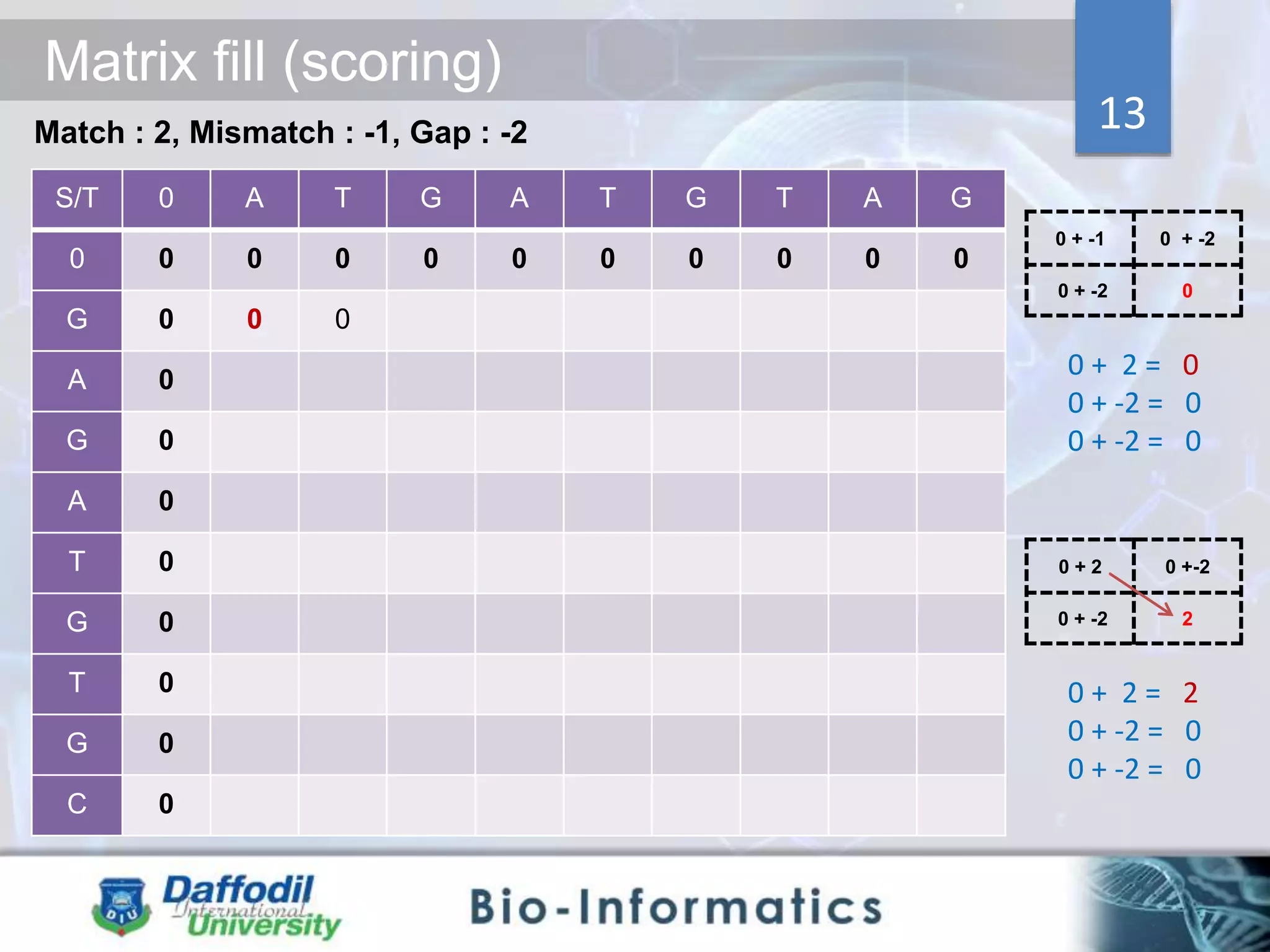
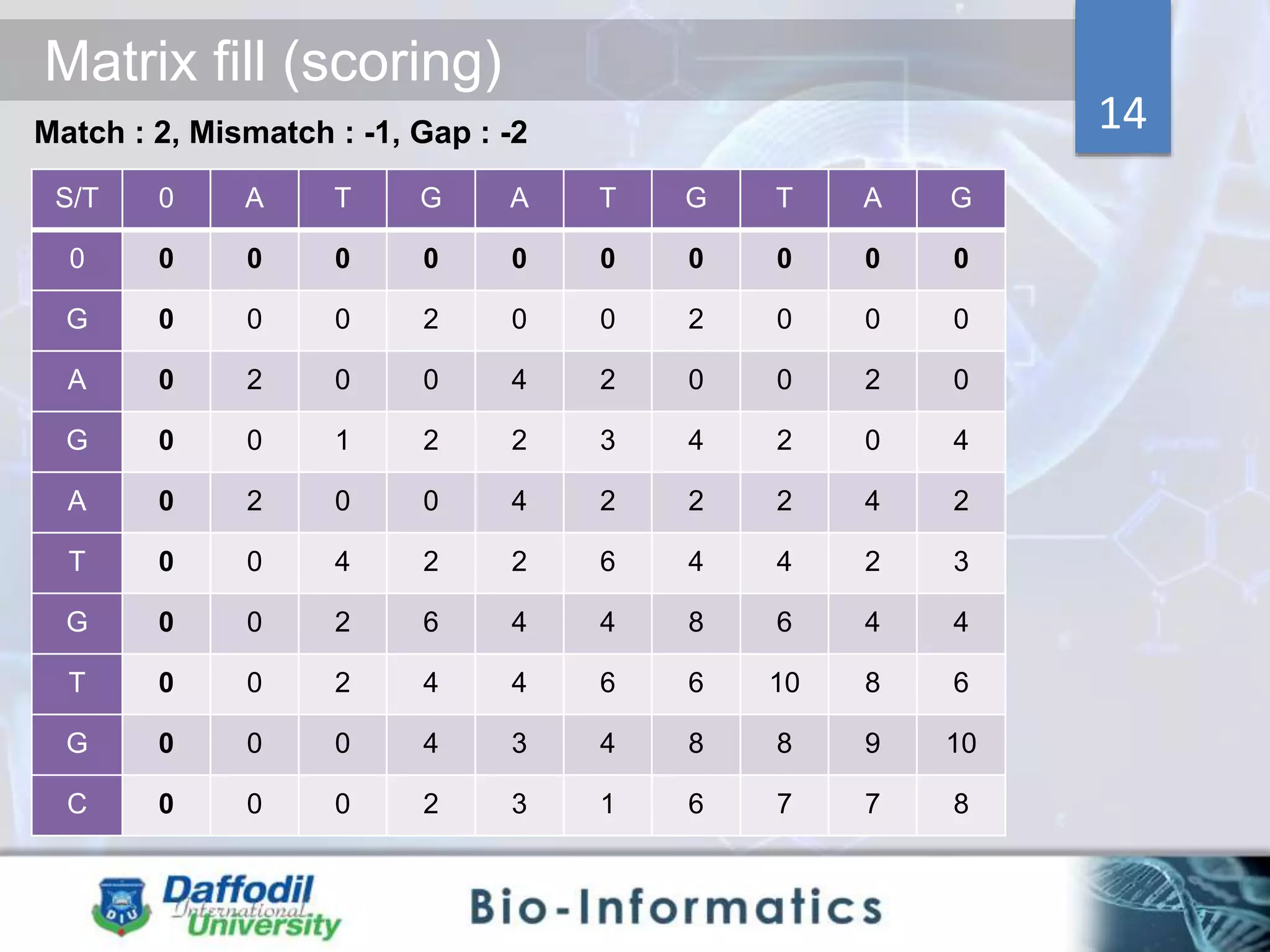
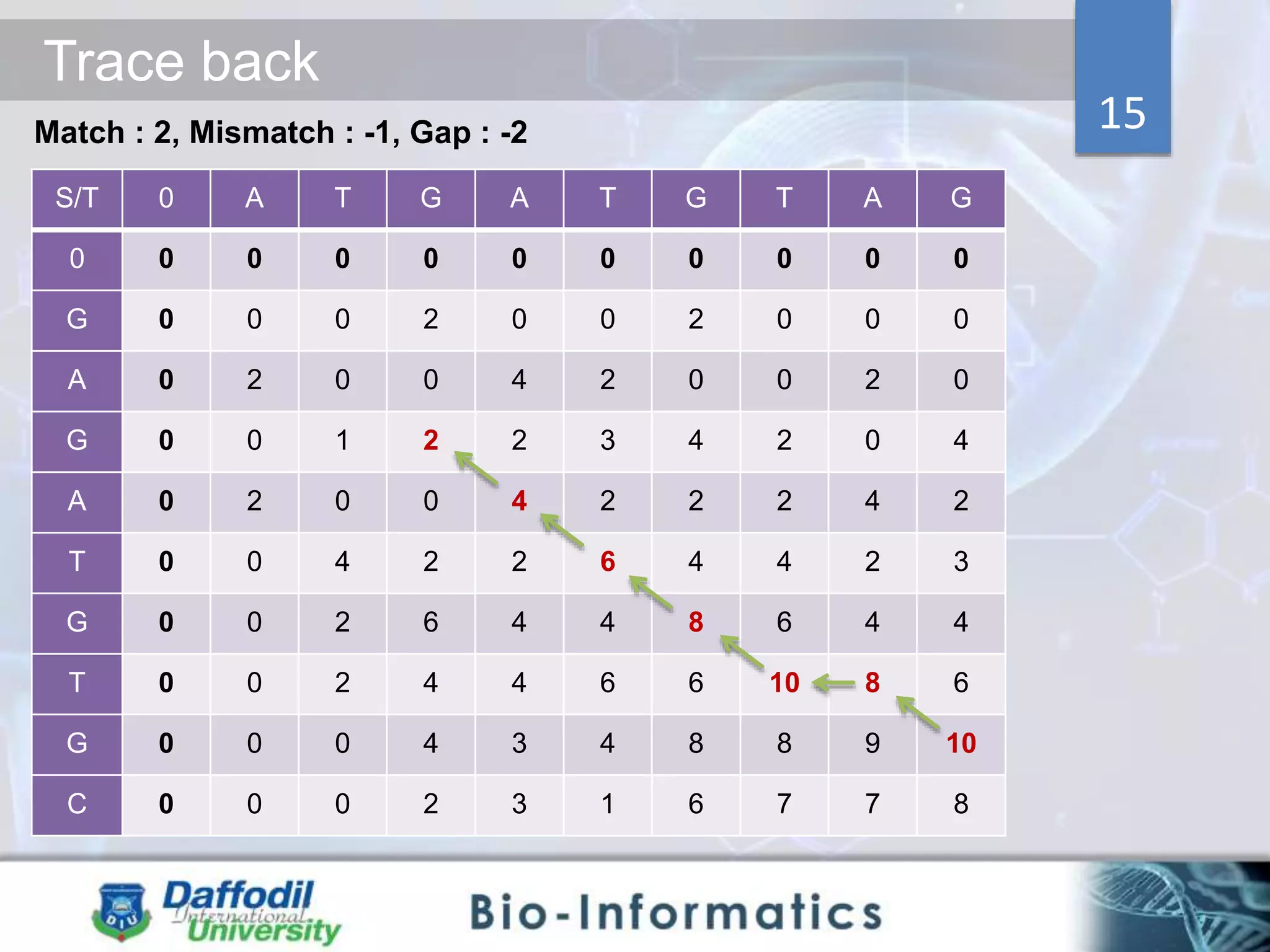
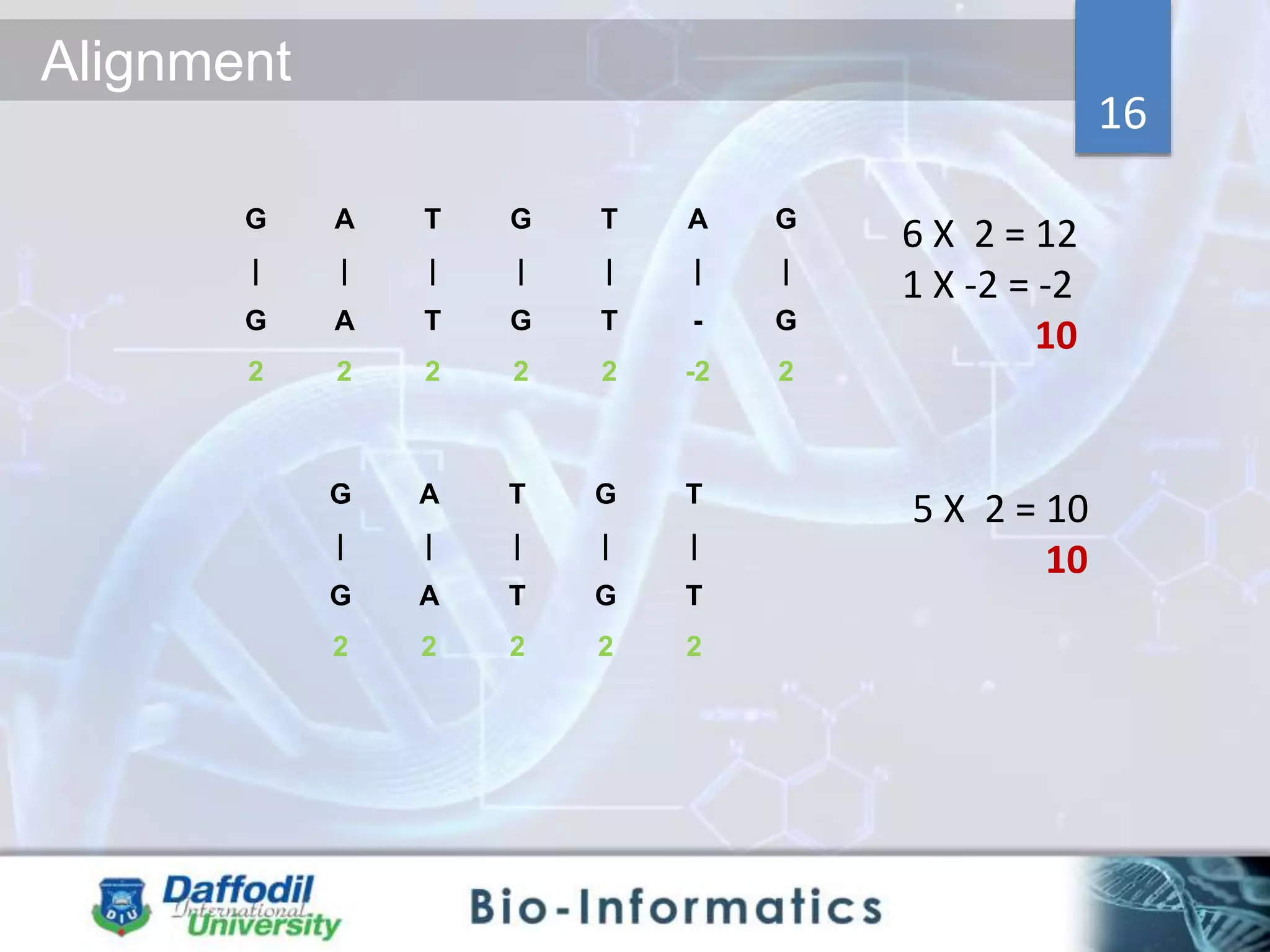
The document discusses sequence alignment, highlighting its importance in discovering functional, structural, and evolutionary relationships among genes and proteins. It explains the differences between global and local alignment techniques, specifically the Needleman-Wunsch algorithm for global alignment and the Smith-Waterman algorithm for local alignment. Detailed steps for scoring, matrix filling, and traceback processes for optimal alignment are provided.

1. 1

2. 2
Group Member
151-15-255 151-15-453 151-15-240 151-15-245

3. 3

4. 4
Why align sequences?
• Useful for discovering
• Functional
• Structural and
• Evolutionary relationship
– For example
• To find whether two (or more) genes or proteins are
evolutionarily related to each other
• Two proteins with similar sequences will probably be
structurally or functionally similar

5. 5
Global Vs Local Alignment
• Global Alignment
– A general global alignment technique is the Needleman–Wunsch
algorithm, which is based on dynamic programming.
– Attempts to align the maximum of the entire sequence
– Suitable for similar and equal length sequences
• Local Alignment
– Local alignments are more useful for
dissimilar sequences that are suspected to contain regions of similarity or
similar sequence motifs within their larger sequence context.
– Stretches of sequences with highest density of matches are
aligned
– Suitable for partially similar, different length and conserved
region containing sequences

6. 6

7. 7
Allows obtaining the optimal alignment with linear gap cost has
been proposed by Needleman and Wunsch by providing a
score, for each position of the aligned sequences.
Based on the dynamic programming technique.
For two sequences of length m and n we define a matrix of
dimensions m+1 and n+1.
Global Alignment

8. 8
Global Alignment
 Three steps in dynamic programming
 Initialization
 Matrix fill (scoring)
 Traceback (alignment)
Smith–Waterman algorithm

9. 9
Sequences:
S: ATTATCT
T: TTTCTA
T
S 0
_
A
T
T
A
T
C
T
_ T T T C T A
0
-1
-2
-3
-4
-5
-6
-7
-1 -2 -3 -4 -5 -6
0 -1 -2 -3 -4 -5
1 2 1 0 -1 -2
0 3 4 3 2 1
-1 2 3 4 3 4
-2 1 4 3 6 5
-3 0 3 6 5 6
-4 -1 2 5 8 7
Match Score =
+2
Mismatch Score
= 0
Gap Penalty = -1

10. 10
0
_
A
T
T
A
T
C
T
_ T T T C T A
0
-1
-2
-3
-4
-5
-6
-7
-1 -2 -3 -4 -5 -6
0 -1 -2 -3 -4 -5
1 2 1 0 -1 -2
0 3 4 3 2 1
-1 2 3 4 3 4
-2 1 4 3 6 5
-3 0 3 6 5 6
-4 -1 2 5 8 7
T
S

11. 11 Optimal Alignment:
S
T
No: of matches = 5
No: of mismatches = 3
(5 x 2) – (3 x -1) = 7
A T T A T C T –
- T T – T C T A

12. 12

13. 13
S/T 0 A T G A T G T A G
0 0 0 0 0 0 0 0 0 0 0
G 0 0 0
A 0
G 0
A 0
T 0
G 0
T 0
G 0
C 0
0 + 2 0 +-2
0 + -2 2
0 + 2 = 2
0 + -2 = 0
0 + -2 = 0
Match : 2, Mismatch : -1, Gap : -2
0 + -1 0 + -2
0 + -2 0
0 + 2 = 0
0 + -2 = 0
0 + -2 = 0
Matrix fill (scoring)

14. 14
S/T 0 A T G A T G T A G
0 0 0 0 0 0 0 0 0 0 0
G 0 0 0 2 0 0 2 0 0 0
A 0 2 0 0 4 2 0 0 2 0
G 0 0 1 2 2 3 4 2 0 4
A 0 2 0 0 4 2 2 2 4 2
T 0 0 4 2 2 6 4 4 2 3
G 0 0 2 6 4 4 8 6 4 4
T 0 0 2 4 4 6 6 10 8 6
G 0 0 0 4 3 4 8 8 9 10
C 0 0 0 2 3 1 6 7 7 8
Match : 2, Mismatch : -1, Gap : -2
Matrix fill (scoring)

15. Trace back
15
S/T 0 A T G A T G T A G
0 0 0 0 0 0 0 0 0 0 0
G 0 0 0 2 0 0 2 0 0 0
A 0 2 0 0 4 2 0 0 2 0
G 0 0 1 2 2 3 4 2 0 4
A 0 2 0 0 4 2 2 2 4 2
T 0 0 4 2 2 6 4 4 2 3
G 0 0 2 6 4 4 8 6 4 4
T 0 0 2 4 4 6 6 10 8 6
G 0 0 0 4 3 4 8 8 9 10
C 0 0 0 2 3 1 6 7 7 8
Match : 2, Mismatch : -1, Gap : -2

16. Alignment
16
G A T G T A G
| | | | | | |
G A T G T - G
2 2 2 2 2 -2 2
6 X 2 = 12
1 X -2 = -2
10
G A T G T
| | | | |
G A T G T
2 2 2 2 2
5 X 2 = 10
10

17. 17

18. 18