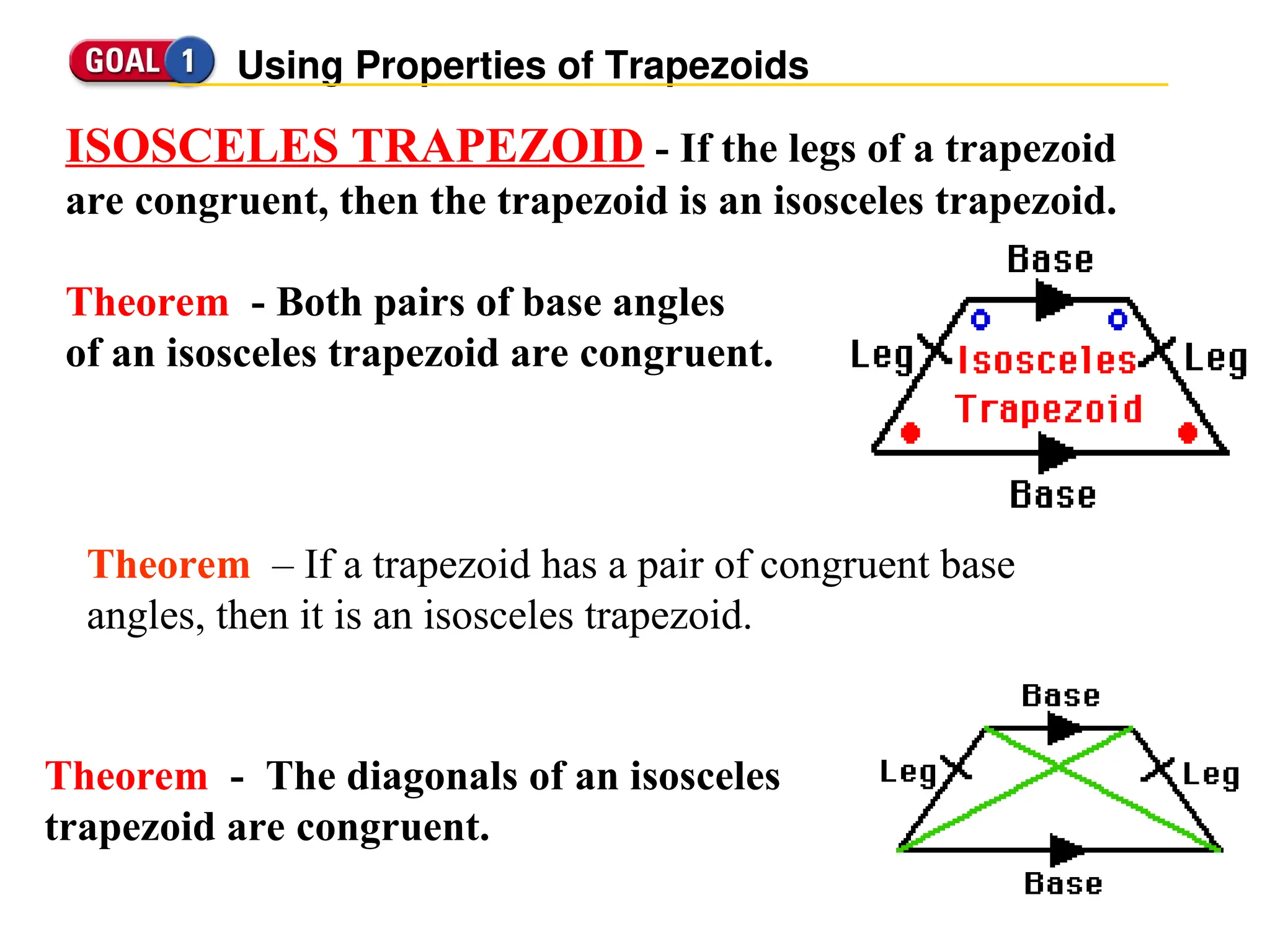
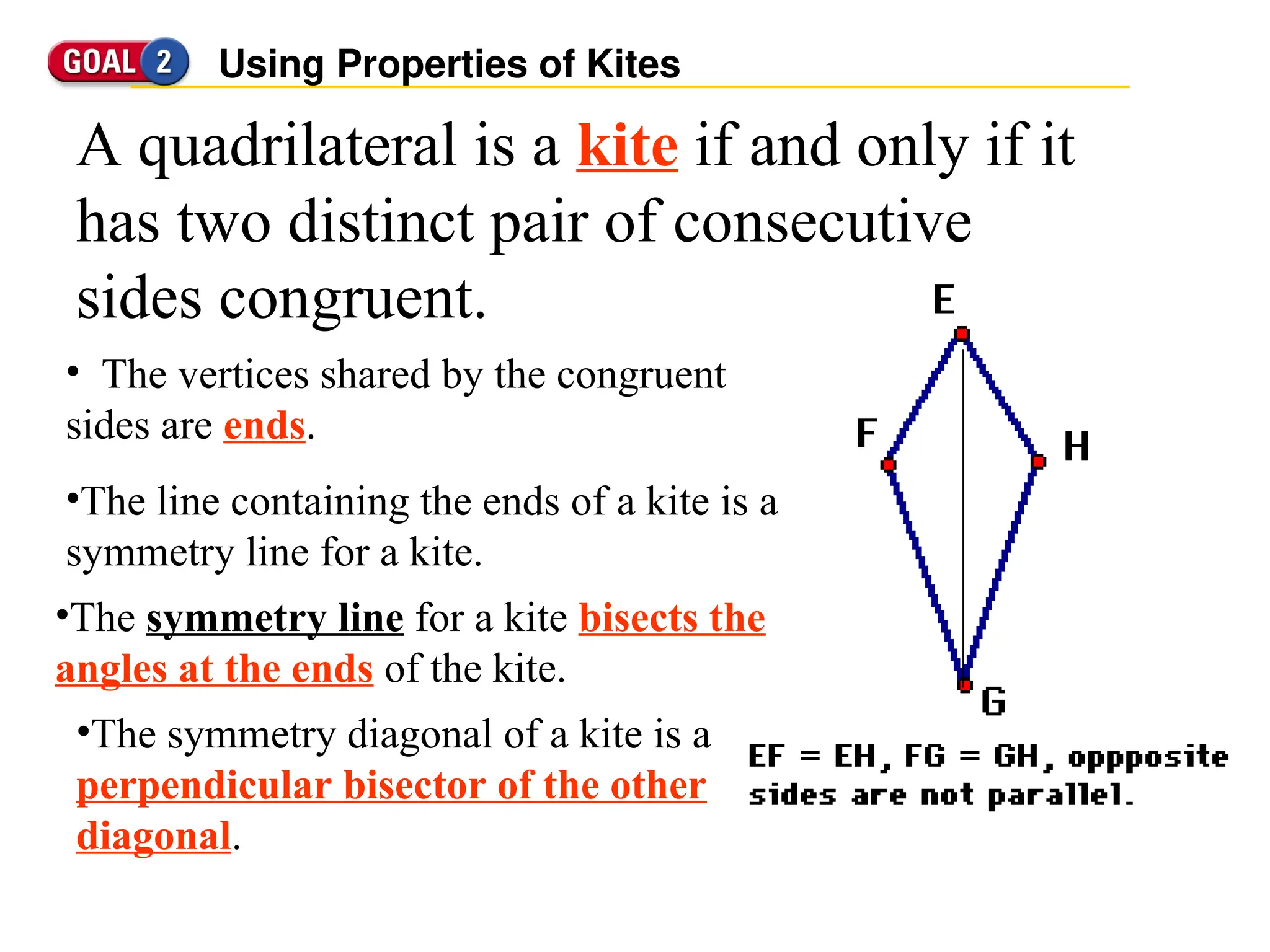
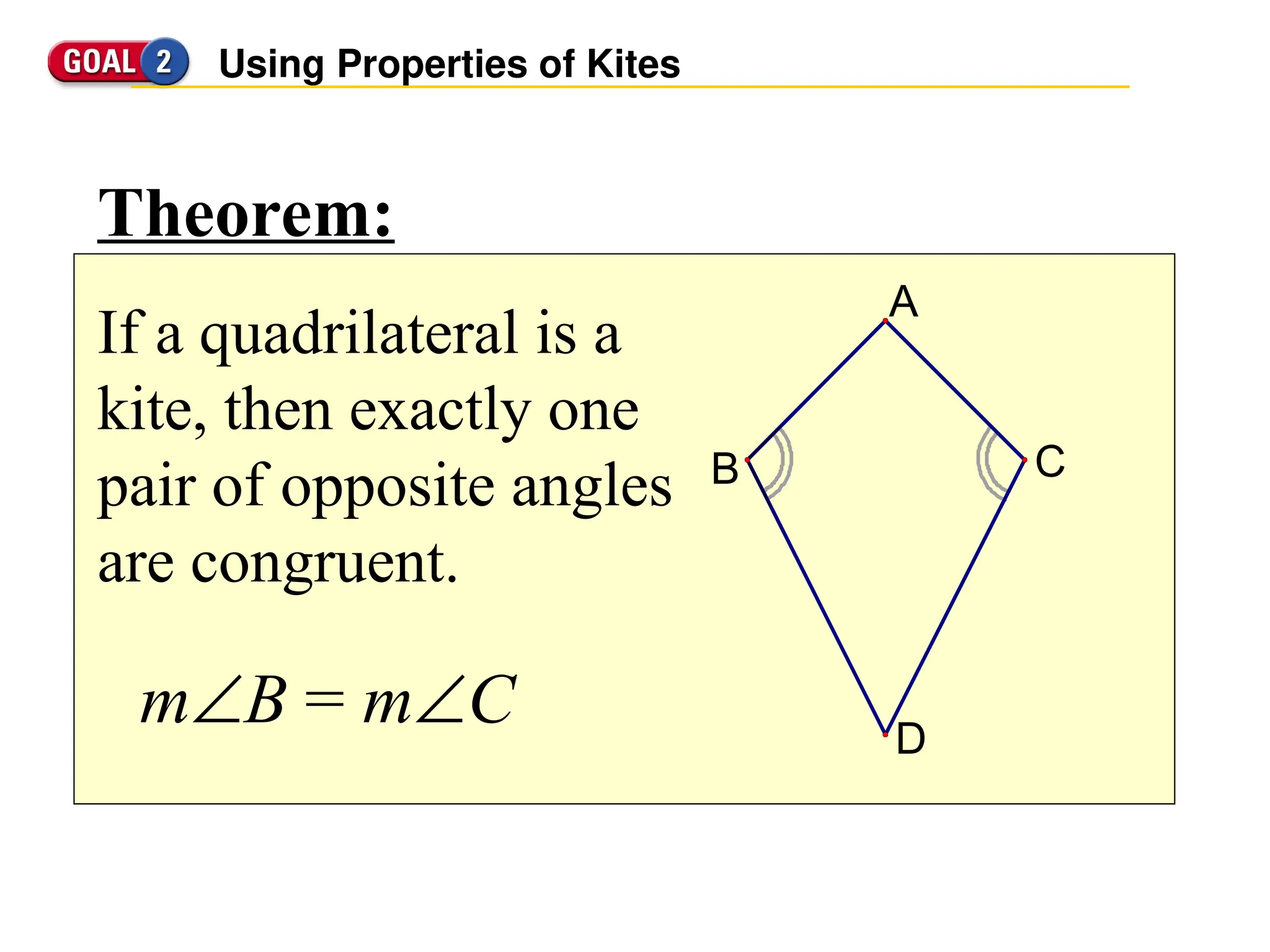
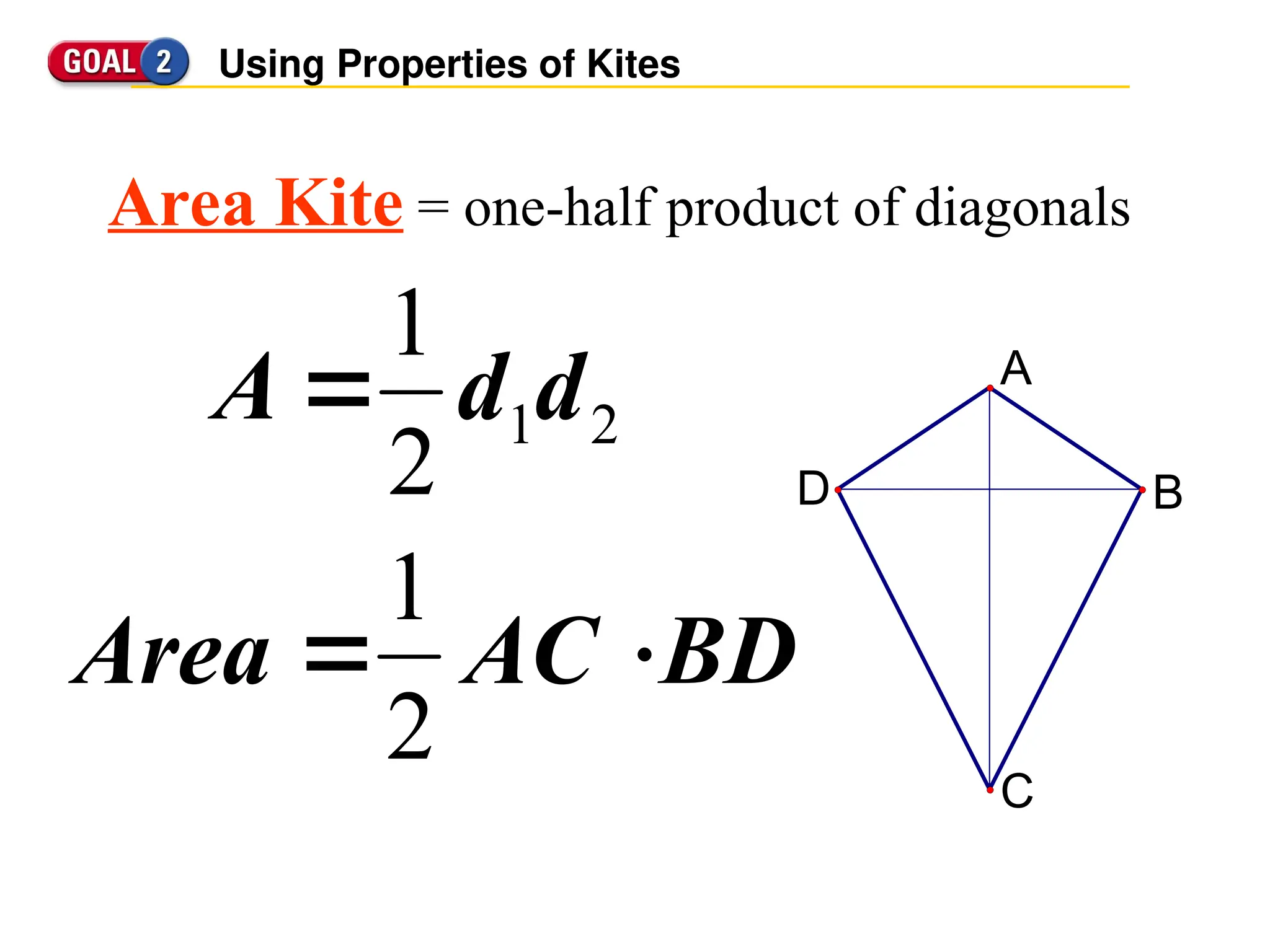
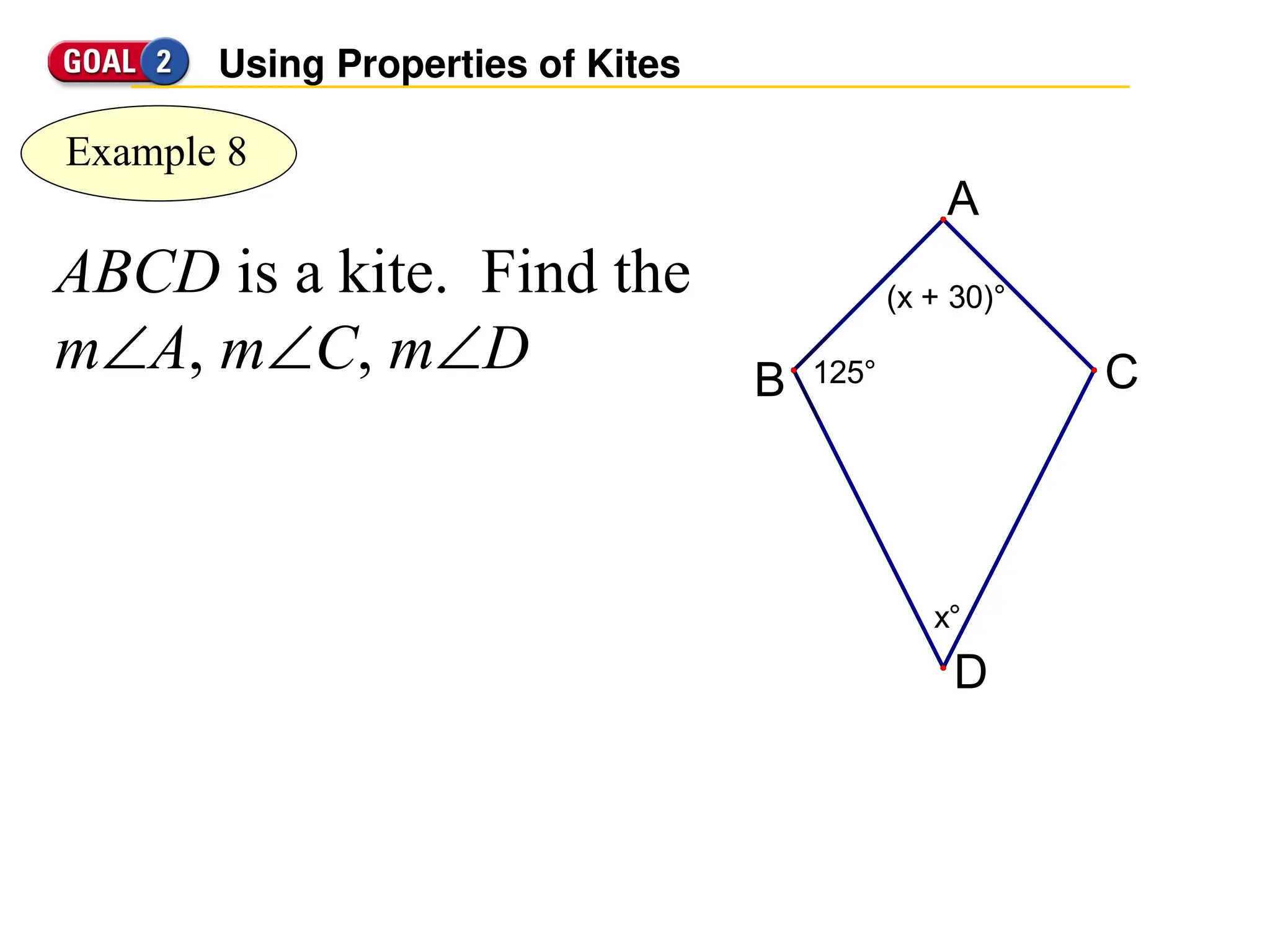
The document defines trapezoids and kites, detailing their properties and theorems. It explains trapezoids as quadrilaterals with one pair of parallel sides, introduces isosceles trapezoids, and discusses the midsegment theorem. It also defines kites, highlighting characteristics like congruent sides and specific angle properties.

1. Trapezoids and Kites
Goal 1 Using Properties of Trapezoids
Goal 2 Using Properties of Kites

2. Trapezoid definition
A Trapezoid is a quadrilateral with only
one pair of parallel sides.
Base
Base
Leg
Leg
1
b
2
b
h
Amgle
Base
Amgle
Base
Amgle
Base
Amgle
Base

3. Using Properties of Trapezoids
A Trapezoid is a quadrilateral with
exactly one pair of parallel sides.
Trapezoid Terminology
• The parallel sides are called BASES.
• The nonparallel sides are called
LEGS.
• There are two pairs of base angles, the
two touching the top base, and the two
touching the bottom base.

4. Using Properties of Trapezoids
ISOSCELES TRAPEZOID - If the legs of a trapezoid
are congruent, then the trapezoid is an isosceles trapezoid.
Theorem - Both pairs of base angles
of an isosceles trapezoid are congruent.
Theorem - The diagonals of an isosceles
trapezoid are congruent.
Theorem – If a trapezoid has a pair of congruent base
angles, then it is an isosceles trapezoid.

5. Using Properties of Trapezoids
Midsegment
A B
C
D
E F
Midsegment of a Trapezoid – segment that
connects the midpoints of the legs of the
trapezoid.

6. Using Properties of Trapezoids
Theorem: Midsegment Theorem for Trapezoids
The midsegment of a trapezoid is parallel to each base and its
length is one-half the sum of the lengths of the bases.
Midsegment
A B
C
D
E F
)
(
2
1
||
;
||
DC
AB
EF
DC
EF
AB
EF



7. DEEPEN
Consider an isosceles trapezoid ABCD, where
AB is parallel to DC, and AD is equal to BC. The
measure of angle DAB is 45 degrees.
What is the measure of angle ADC? And why?

8. Using Properties of Kites
Example 7
QRST is an
isosceles
trapezoid. Find
the measure of
each angle.

9. Using Properties of Kites
Example 7
Find the length
of MN.

10. Using Properties of Kites

11. Using Properties of Kites
A quadrilateral is a kite if and only if it
has two distinct pair of consecutive
sides congruent.
• The vertices shared by the congruent
sides are ends.
•The symmetry diagonal of a kite is a
perpendicular bisector of the other
diagonal.
•The line containing the ends of a kite is a
symmetry line for a kite.
•The symmetry line for a kite bisects the
angles at the ends of the kite.

12. Using Properties of Kites
A
B C
D
Theorem:
If a quadrilateral is a
kite, then exactly one
pair of opposite angles
are congruent.
mB = mC

13. Using Properties of Kites
D
A
B
C
Area Kite = one-half product of diagonals
2
1
2
1
d
d
A 
BD
AC
Area 

2
1

14. Using Properties of Kites
29
Example 7
CBDE is a Kite.
Find AC.
5
B
C
D
E
A

15. Using Properties of Kites
x°
125°
(x + 30)°
A
B C
D
Example 8
ABCD is a kite. Find the
mA, mC, mD