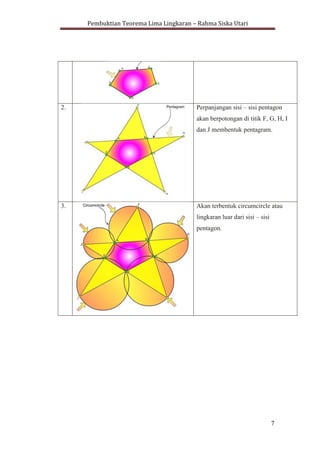
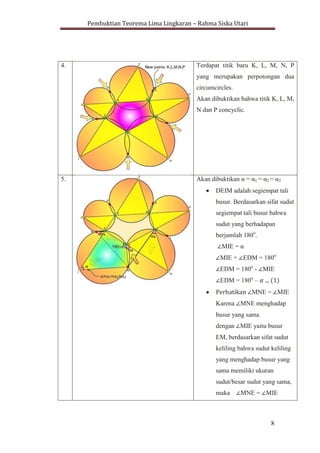
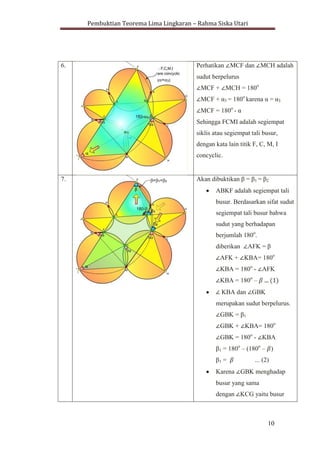
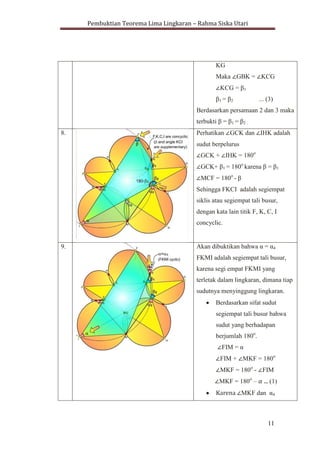
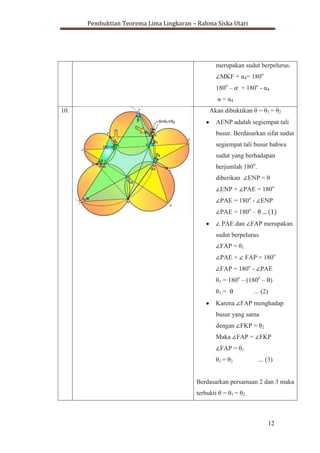
Dokumen ini membahas pembuktian teorema lima lingkaran, yang menyatakan bahwa suatu lingkaran dapat dibentuk dari segilima tidak beraturan. Teorema ini dijelaskan menggunakan konsep geometris seperti pentagon, pentagram, segiempat tali busur, dan sifat sudut dalam lingkaran. Hasilnya menunjukkan bahwa titik-titik tertentu dari perpotongan lingkaran adalah concyclic, mengkonfirmasi teorema tersebut.