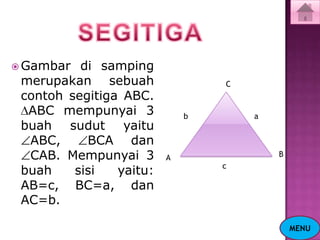
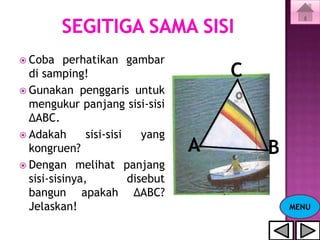
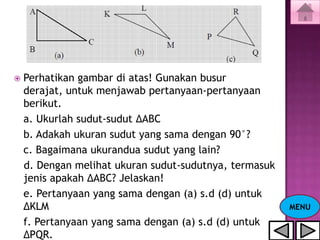
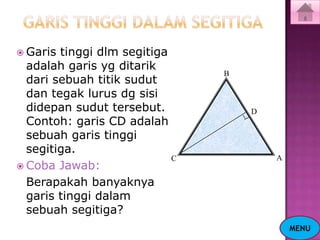
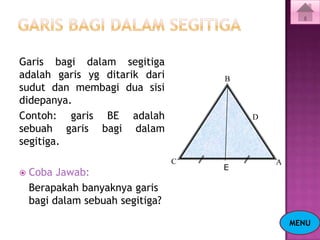
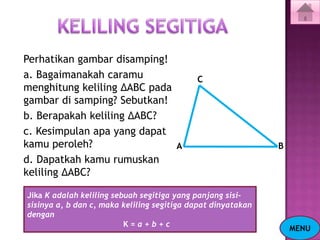
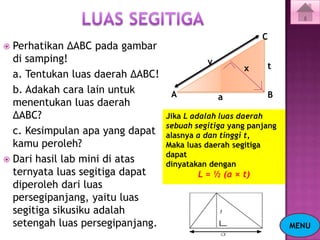
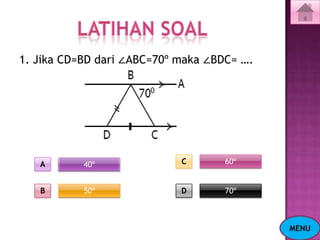
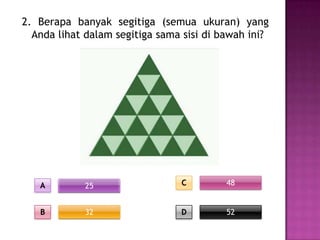
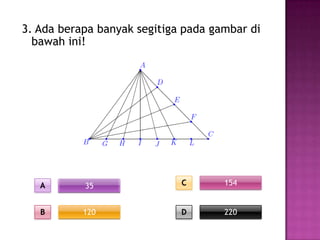
Dokumen ini menjelaskan tentang konsep segitiga, termasuk jenis-jenis segitiga berdasarkan sisi dan sudut, serta cara menghitung keliling dan luasnya. Selain itu, terdapat juga penjelasan mengenai garis tinggi dan garis bagi dalam segitiga. Latihan soal disertakan untuk memperkuat pemahaman materi.

1. Disusun oleh:
Dewi Yanwari Madyaratri
(11310236)
MULAI

2. STANDAR KOMPETENSI
KOMPETENSI DASAR
SEGITIGA
JENIS – JENIS SEGITIGA
GARIS TINGGI
GARIS BAGI
KELILING
LUAS
LATIHAN SOAL

3.  Standar Kompetensi
 Memahami konsep segiempat dan segitiga
serta menentukan ukurannya.
MENU

4.  Kompetensi Dasar
 Mengidentifikasi sifat-sifat segitiga
berdasarkan sisi sudutnya.
 Menghitung keliling dan luas bangun segitiga
serta menggunakannya dalam pemecahan
masalah.
 Melukis segitiga, garis tinggi dan garis bagi.
MENU

5.  Gambar di samping
merupakan sebuah C
contoh segitiga ABC.
ABC mempunyai 3 b a
buah sudut yaitu
ABC, BCA dan
CAB. Mempunyai 3 A B
c
buah sisi yaitu:
AB=c, BC=a, dan
AC=b.
MENU

6. MENU

7.  Coba perhatikan gambar di
samping!
 Gunakan penggaris untuk B
mengukur panjang sisi-sisi
ΔABC.
 Adakah sisi-sisi yang
kongruen?
C
 Dengan melihat panjang A
sisi-sisinya, disebut bangun
apakah ΔABC? Jelaskan!
MENU

8.  Coba Perhatikan Gambar di
samping! C
 Gunakan penggaris untuk
mengukur panjang sisi-sisi
ΔABC.
 Adakah sisi-sisi yang kongruen?
 Dengan melihat panjang sisi-
sisinya, disebut bangun apakah
ΔABC? Jelaskan! A B
MENU

9.  Coba perhatikan gambar
di samping! C
 Gunakan penggaris untuk
mengukur panjang sisi-sisi
ΔABC.
 Adakah sisi-sisi yang
kongruen? A B
 Dengan melihat panjang
sisi-sisinya, disebut
bangun apakah ΔABC?
Jelaskan! MENU

10.  Berdasarkan besar sudutnya, segitiga dibagi
menjadi tiga jenis, yaitu
1. Segitiga lancip
2. Segitiga tumpul
3. Segitiga siku-siku
MENU

11.  Perhatikan gambar di atas! Gunakan busur
derajat, untuk menjawab pertanyaan-pertanyaan
berikut.
a. Ukurlah sudut-sudut ΔABC
b. Adakah ukuran sudut yang sama dengan 90°?
c. Bagaimana ukurandua sudut yang lain?
d. Dengan melihat ukuran sudut-sudutnya, termasuk
jenis apakah ΔABC? Jelaskan!
e. Pertanyaan yang sama dengan (a) s.d (d) untuk
ΔKLM MENU
f. Pertanyaan yang sama dengan (a) s.d (d) untuk
ΔPQR.

12.  Maka, kita memperoleh kesimpulan:
 Segitiga
yang ukuran salah satu sudutnya
90° disebut segitiga siku-siku.
 Segitiga
yang salah satu ukuran sudutnya
tumpul disebut segitiga tumpul.
 Segitiga
yang ketiga ukuran sudutnya lancip
disebut segitiga lancip.
MENU

13.  Garis tinggi dlm segitiga
adalah garis yg ditarik
B
dari sebuah titik sudut
dan tegak lurus dg sisi
didepan sudut tersebut. D
Contoh: garis CD adalah
sebuah garis tinggi
segitiga.
C A
 Coba Jawab:
Berapakah banyaknya
garis tinggi dalam
sebuah segitiga?
MENU

14. Garis bagi dalam segitiga
adalah garis yg ditarik dari B
sudut dan membagi dua sisi
didepanya.
Contoh: garis BE adalah D
sebuah garis bagi dalam
segitiga.
C A
E
 Coba Jawab:
Berapakah banyaknya garis
bagi dalam sebuah segitiga?
MENU

15. Perhatikan gambar disamping!
a. Bagaimanakah caramu C
menghitung keliling ΔABC pada
gambar di samping? Sebutkan!
b. Berapakah keliling ΔABC?
c. Kesimpulan apa yang dapat
kamu peroleh? A B
d. Dapatkah kamu rumuskan
keliling ΔABC?
Jika K adalah keliling sebuah segitiga yang panjang sisi-
sisinya a, b dan c, maka keliling segitiga dapat dinyatakan
dengan
K=a+b+c
MENU

16. C
 Perhatikan ΔABC pada gambar
di samping! y
x t
a. Tentukan luas daerah ΔABC!
b. Adakah cara lain untuk A B
a
menentukan luas daerah
ΔABC? Jika L adalah luas daerah
sebuah segitiga yang panjang
c. Kesimpulan apa yang dapat alasnya a dan tinggi t,
kamu peroleh? Maka luas daerah segitiga
dapat
 Dari hasil lab mini di atas
dinyatakan dengan
ternyata luas segitiga dapat L = ½ (a × t)
diperoleh dari luas
persegipanjang, yaitu luas
segitiga sikusiku adalah
setengah luas persegipanjang. MENU

17. 1. Jika CD=BD dari ∠ABC=70º maka ∠BDC= ….
A 40º C 60º
B 50º D 70º
MENU

18. NEXT

19. ULANGI

20. 2. Berapa banyak segitiga (semua ukuran) yang
Anda lihat dalam segitiga sama sisi di bawah ini?
A 25 C 48
B 32 D 52

21. NEXT

22. ULANGI

23. 3. Ada berapa banyak segitiga pada gambar di
bawah ini!
A 35 C 154
B 120 D 220

24. KLIK

25. ULANGI

26. MENU