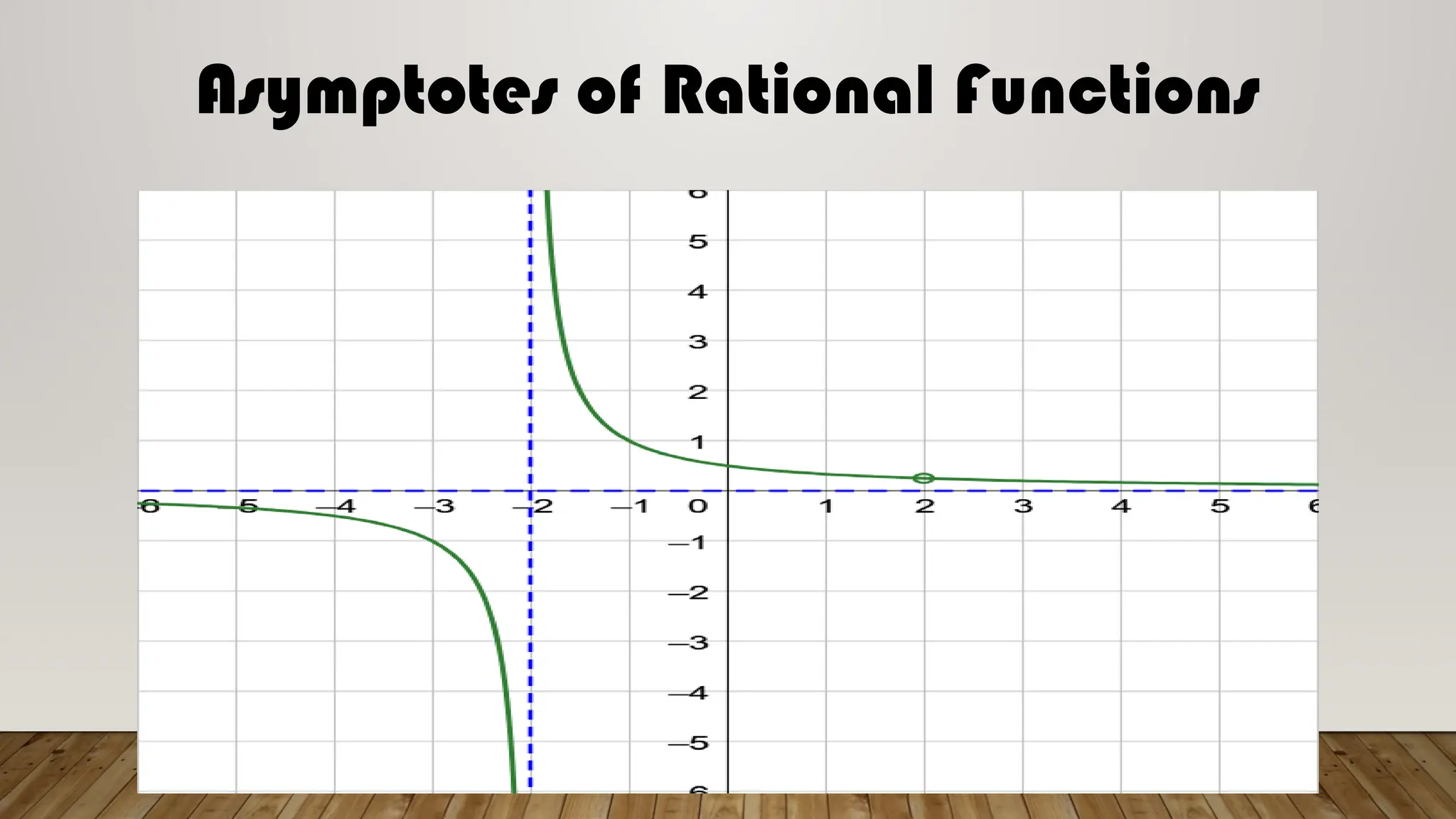
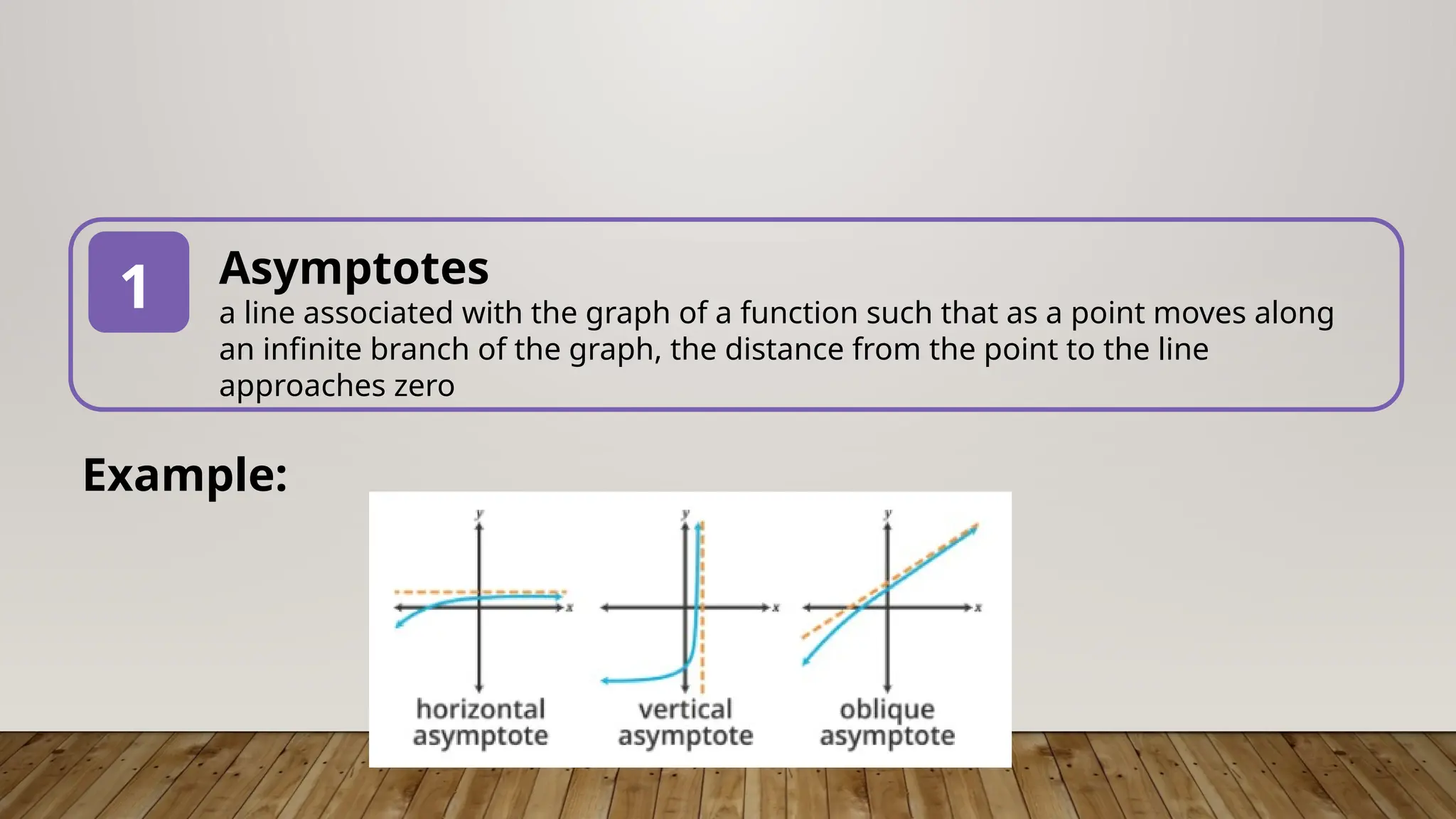
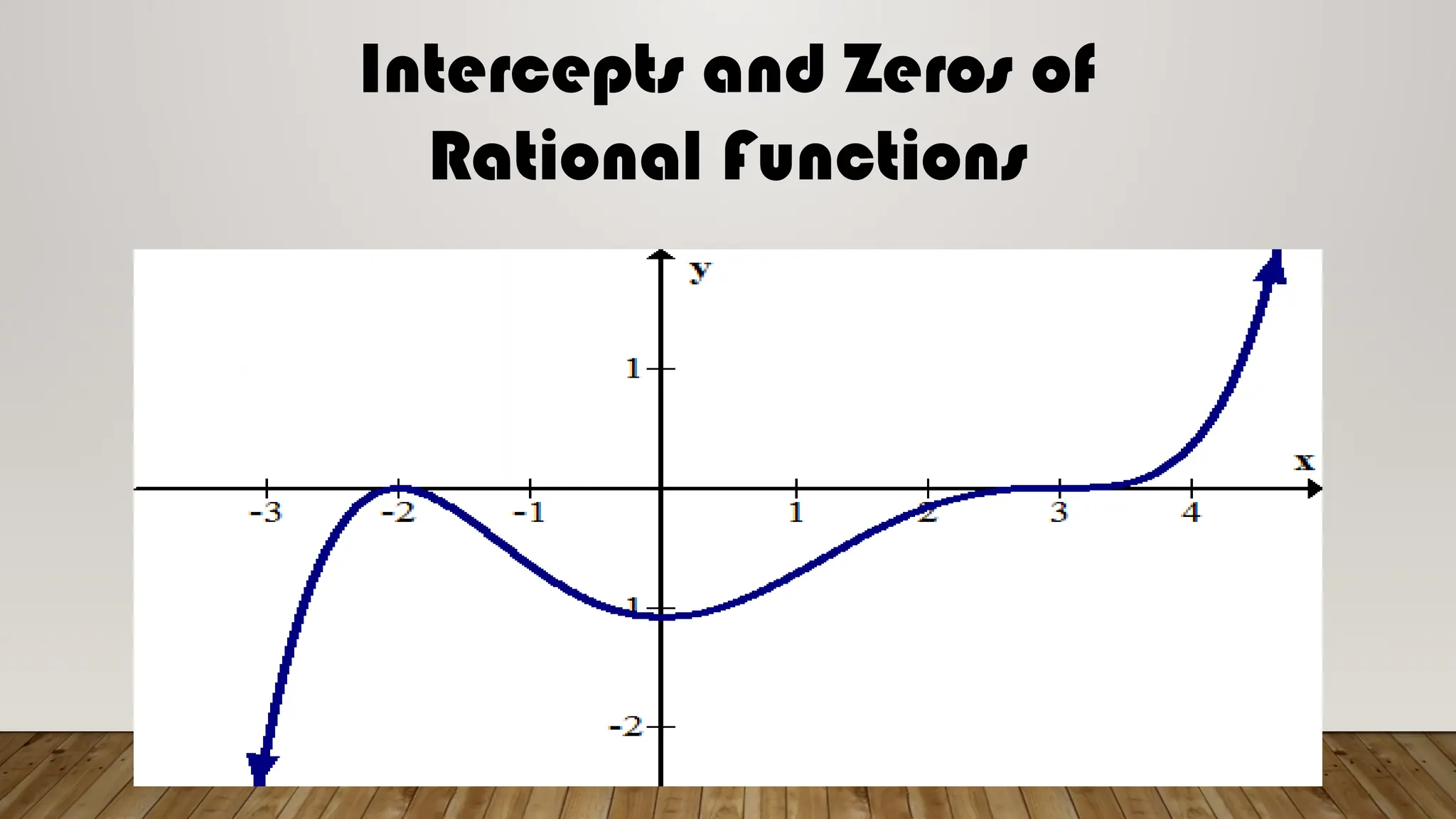
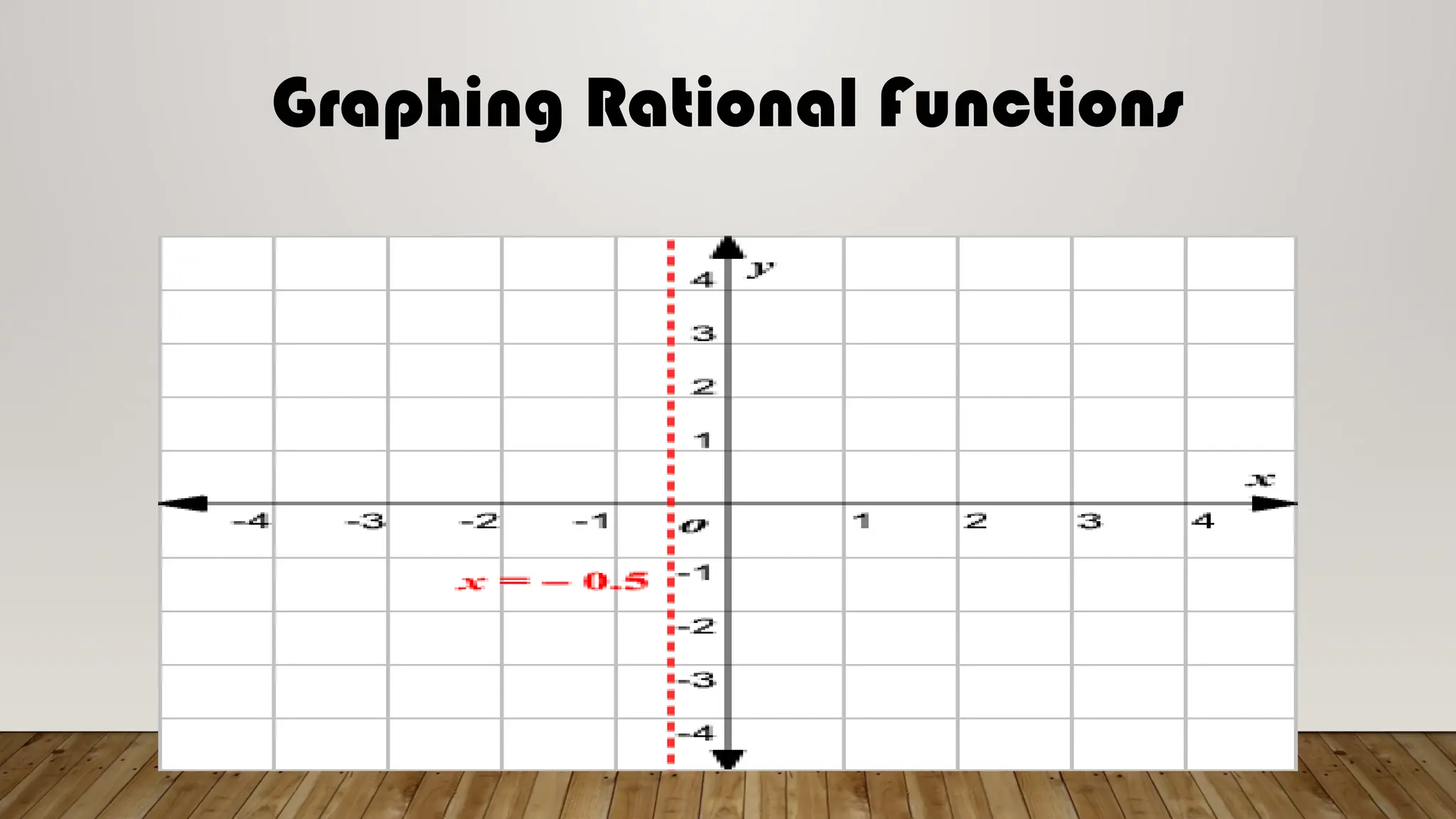
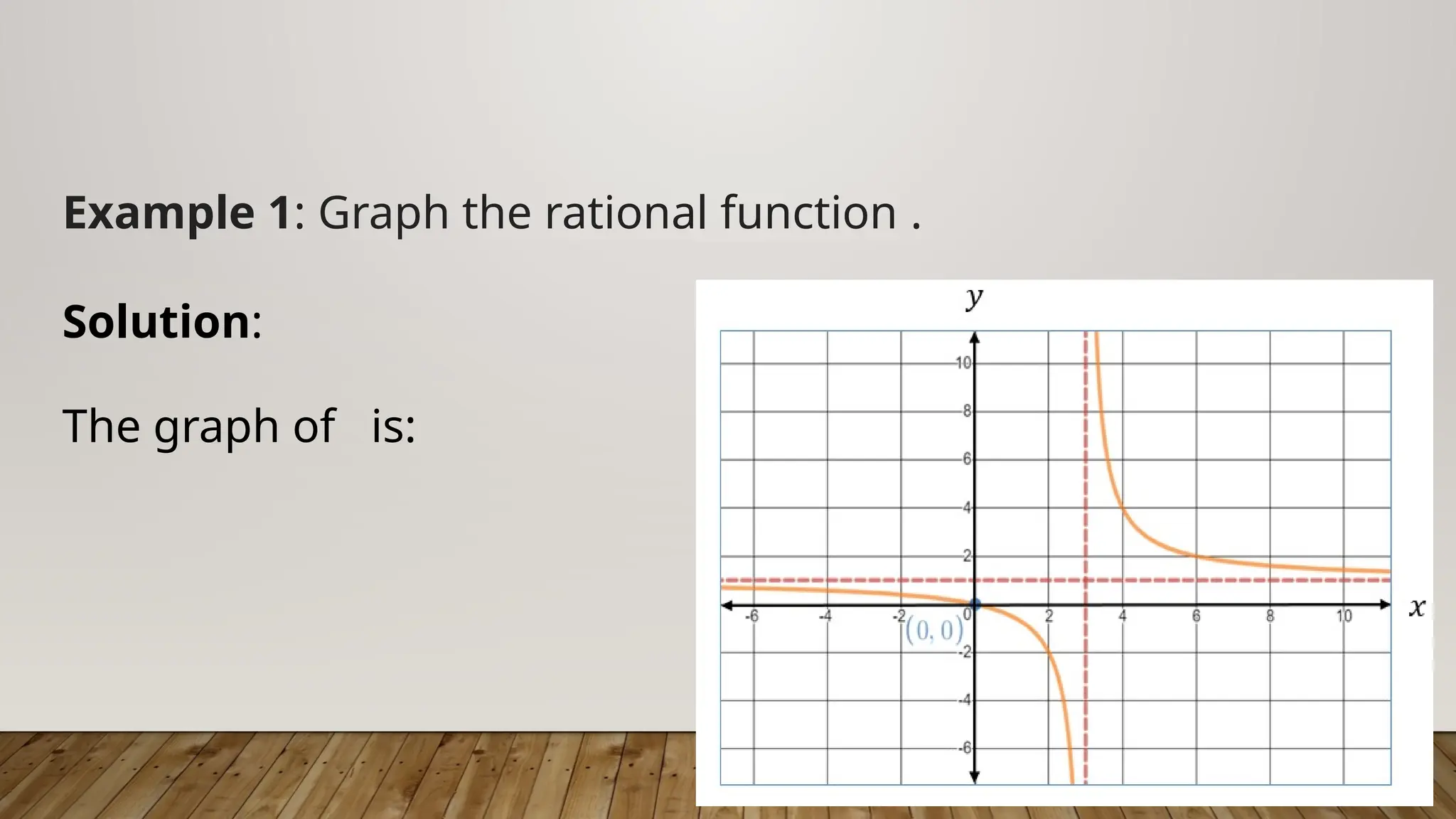
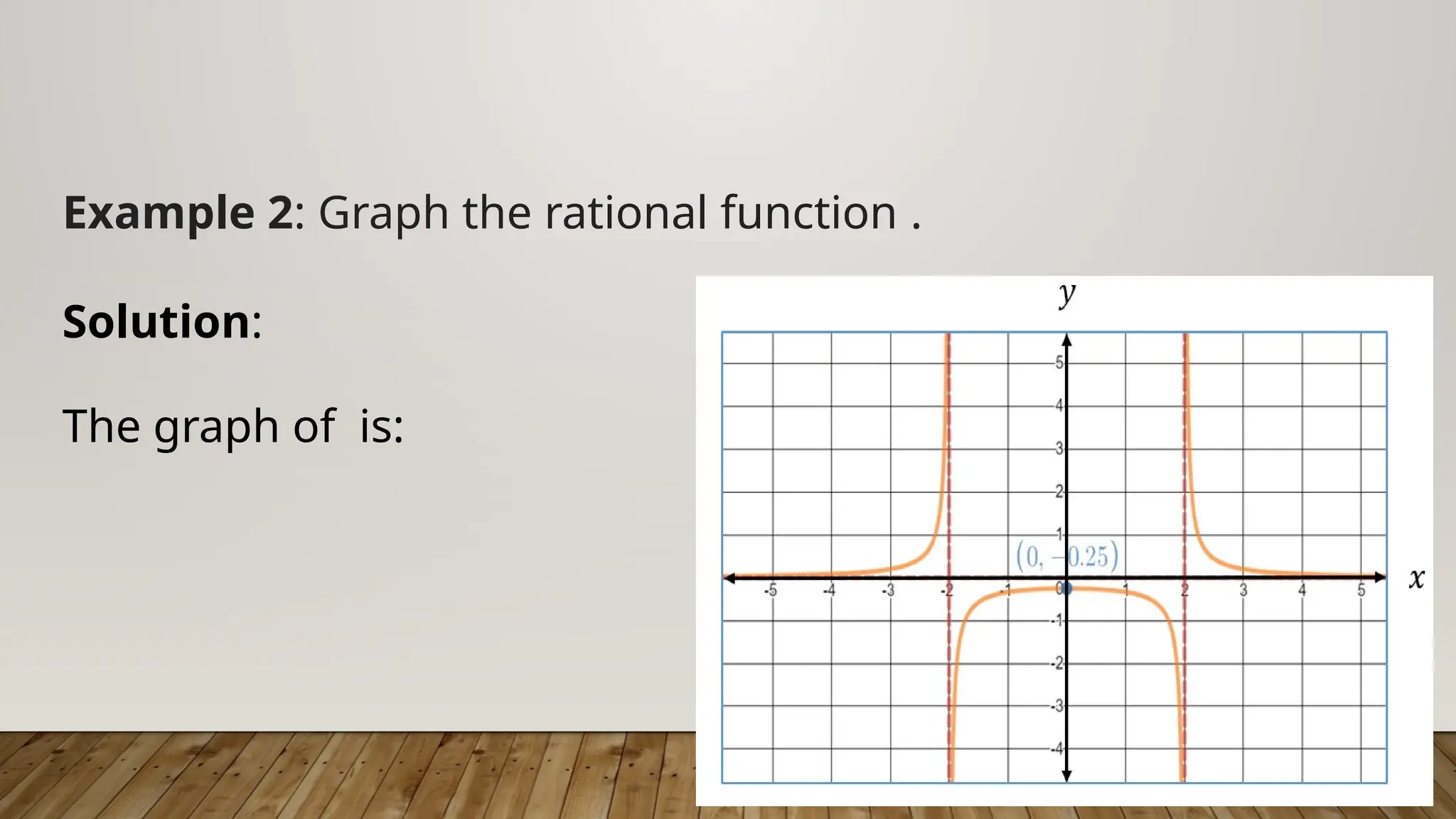
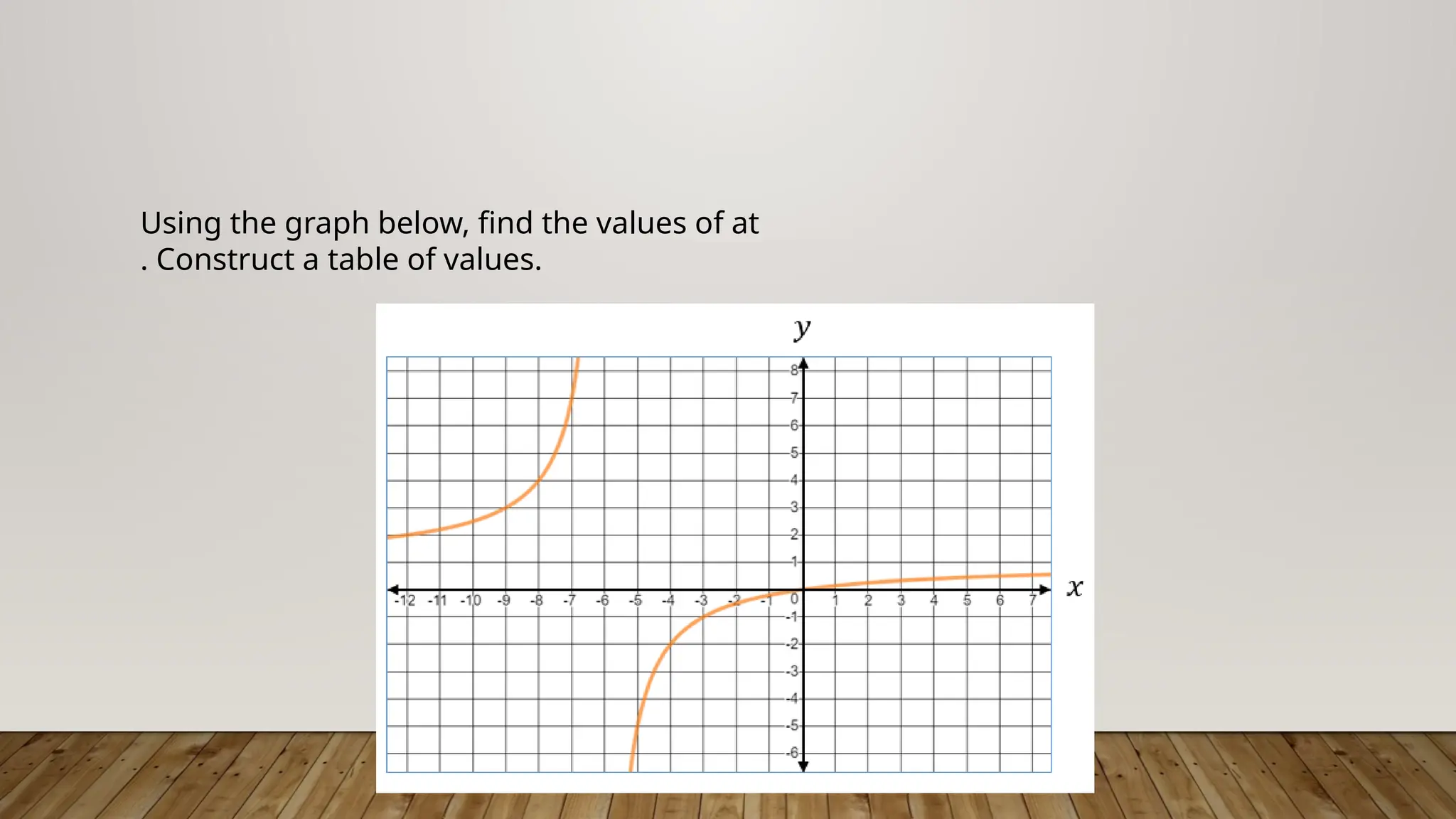
The document provides a comprehensive guide on understanding asymptotes, intercepts, and zeros of rational functions, detailing how to identify and solve for these elements through examples. It outlines the methods for graphing rational functions and establishes guidelines for solving real-world problems involving rational functions. Additionally, it emphasizes the mathematical processes involved in analyzing rational functions, including the significance of degrees of polynomials in determining horizontal asymptotes.

1. Asymptotes of Rational Functions

2. ● How will you determine the asymptotes of rational
functions?
● How will you solve problems involving the asymptotes of
rational functions?

3. Asymptotes
a line associated with the graph of a function such that as a point moves along
an infinite branch of the graph, the distance from the point to the line
approaches zero
1
Example:

4. 2 Vertical Asymptote
It is a vertical line with an equation that satisfies the following properties:
• either increases or decreases without bound as approaches the number from
the right
• either increases or decreases without bound as approaches the number from
the left
Example:

5. 3 Horizontal Asymptote
It is a horizontal line with an equation that satisfies the following properties:
• approaches the number from above or below as gets infinitely small
• approaches the number from above or below as gets infinitely large
Example:

6. horizontal asymptote of a rational function
determined by comparing the degree of the polynomials in the numerator and
denominator:
• If the numerator has a degree higher than that of the denominator, there is
no horizontal asymptote, but it may have an oblique asymptote instead.
• If the degree of the numerator is equal to the degree of the denominator, the
horizontal asymptote is at the -value equal to the ratio of the leading
coefficients of the numerator and the denominator.
• If the degree of the numerator is less than the degree of the denominator, the
horizontal asymptote is .
4

7. Example 1: Determine the asymptotes of the rational
function

8. Example 1: Determine the asymptotes of the rational
function
Solution:
For the vertical asymptote, solve for the zero of the
denominator.

9. Example 1: Determine the asymptotes of the rational
function
Solution:
Equate the denominator to zero.

10. Example 1: Determine the asymptotes of the rational
function
Solution:
Equate the denominator to zero.
Solve for the equation.

11. Example 1: Determine the asymptotes of the rational
function
Solution:
Thus, the vertical asymptote of the given rational function
is .

12. Example 1: Determine the asymptotes of the rational
function
Solution:
For the horizontal asymptote, compare the degrees of the
numerator and denominator.

13. Example 1: Determine the asymptotes of the rational
function
Solution:
Degree of the numerator: 1
Degree of the denominator: 1

14. Example 1: Determine the asymptotes of the rational
function
Solution:
Since the degree of the numerator is equal to the degree of
the denominator, the horizontal asymptote is equal to the
quotient of the leading coefficients of the numerator and the
denominator.

15. Example 1: Determine the asymptotes of the rational
function
Solution:
leading coefficient of numerator: 1
leading coefficient of denominator: 3

16. Example 1: Determine the asymptotes of the rational
function
Solution:
leading coefficient of numerator: 1
leading coefficient of denominator: 3
horizontal asymptote:

17. Example 1: Determine the asymptotes of the rational
function
Solution:
Thus, the horizontal asymptote of the given rational function
is .

18. Example 2: Determine the asymptotes of the rational
function

19. Example 2: Determine the asymptotes of the rational
function
Solution:
For the vertical asymptote, solve for the zero of the
denominator.

20. Example 2: Determine the asymptotes of the rational
function
Solution:
Equate the denominator to zero.

21. Example 2: Determine the asymptotes of the rational
function
Solution:
Equate the denominator to zero.
Solve for the equation.

22. Example 2: Determine the asymptotes of the rational
function
Solution:
Thus, the vertical asymptotes of the given rational function
are and .

23. Example 2: Determine the asymptotes of the rational
function
Solution:
For the horizontal asymptote, compare the degrees of the
numerator and denominator.

24. Example 2: Determine the asymptotes of the rational
function
Solution:
Degree of the numerator: 1
Degree of the denominator: 2

25. Example 2: Determine the asymptotes of the rational
function
Solution:
Since the degree of the numerator is less than the degree of
the denominator, the horizontal asymptote is equal to zero.

26. Example 2: Determine the asymptotes of the rational
function
Solution:
Thus, the horizontal asymptote of the given rational function
is .

27. Individual Practice:
1. Determine the asymptotes of the rational function .
2. Determine the asymptotes of the rational function .

28. Group Practice: To be done in groups with 2 – 5 members
each
The concentration of a drug injected into a patient’s
𝐷
bloodstream after minutes is denoted by the rational
𝑡
function . Determine the asymptotes of the function.

29. 1
Asymptotes
It is a line associated with the graph of a function such that as a point moves
along an infinite branch of the graph, the distance from the point to the line
approaches zero.
1
2 Vertical Asymptote
It is a vertical line with an equation that satisfies the following properties:
• either increases or decreases without bound as approaches the number from
the right
• either increases or decreases without bound as approaches the number from
the left

30. 1
3 Horizontal Asymptote
It is a horizontal line with an equation that satisfies the following properties:
• approaches the number from above or below as gets infinitely small
• approaches the number from above or below as gets infinitely large

31. Intercepts and Zeros of
Rational Functions

32. ● How will you solve for the intercepts and zeroes of
rational functions?
● How will you solve problems involving the intercepts and
zeroes of rational functions?

33. Rational Function
a function of the form where and are both polynomials and
1
Example:
is a rational function.

34. Intercepts of Rational Functions
refers to the intersection of the graph of a rational function to the and axes
2
Example:
The intercept of the function is while its intercept is

35. 3 Zeros of Rational Functions
refers to the value of that would make the function equal to zero; also the same
𝑥
with the -intercept/s of a rational function
𝑥
Example:
The zeros of the rational function are and .

36. Example 1: Determine the zeros of the rational function
.

37. Example 1: Determine the zeros of the rational function
.
Solution:
Equate the numerator to zero.

38. Example 1: Determine the zeros of the rational function
.
Solution:
Solve the equation.

39. Example 1: Determine the zeros of the rational function
.
Solution:
Solve the equation.
The values of that will make the equation equal to zero are
and .

40. Example 1: Determine the zeros of the rational function
.
Solution:
Thus, the zeros of the given rational function are and .

41. Example 2: Determine the intercepts of the rational function
.

42. Example 2: Determine the intercepts of the rational function
.
Solution:
For the intercepts, equate the numerator to zero.

43. Example 2: Determine the intercepts of the rational function
.
Solution:
Solve the equation.

44. Example 2: Determine the intercepts of the rational function
.
Solution:
Solve the equation.
Group the terms.

45. Example 2: Determine the intercepts of the rational function
.
Solution:
Factor the GCF for each group.

46. Example 2: Determine the intercepts of the rational function
.
Solution:
Factor the GCF for each group.
Factor .

47. Example 2: Determine the intercepts of the rational function
.
Solution:
Factor .

48. Example 2: Determine the intercepts of the rational function
.
Solution:
Factor .
Solve for the zeros.

49. Example 2: Determine the intercepts of the rational function
.
Solution:
Thus, the intercepts of the given rational function are , and .

50. Example 2: Determine the intercepts of the rational function
.
Solution:
For the intercept, evaluate .

51. Example 2: Determine the intercepts of the rational function
.
Solution:
Simplify.

52. Example 2: Determine the intercepts of the rational function
.
Solution:
Thus, the intercept of the given rational function is .

53. Individual Practice:
1. Determine the zeros of the rational function .
2. Determine the intercepts of the rational function

54. Group Practice: To be done in groups with 2 to 5 members
The time (in seconds) it takes for a boat with a speed to
travel a certain river going downstream is denoted by the
function Determine the -intercept of the given function and
interpret the result.

55. Intercepts of Rational Functions
This refers to the intersection of the graph of a rational function to the and axes.
2
3 Zeros of Rational Functions
This refers to the value of that would make the function equal to zero. This is
𝑥
also the same with the -intercept/s of a rational function.
𝑥
Rational Function
a function of the form where and are both polynomials and
1

56. Graphing Rational Functions

57. ● How can you describe the graph of a rational function?
● How can you graph a rational function using its
intercepts and asymptotes?

58. -intercept(s) of a rational function
-value(s) that make the numerator zero but are not zeros of the denominator
1
Example:
The -intercept of the function is because the numerator is
zero when .

59. -intercept of a rational function
obtained by evaluating the function at
2
Example:
The -intercept of the function is because .

60. vertical asymptote(s) of a rational function
-value(s) that make the denominator zero but are not zeros of the numerator
3
Example:
The line is a vertical asymptote of the function
because the denominator when .

61. horizontal asymptote of a rational function
determined by comparing the degree of the polynomials in the numerator and
denominator:
• If the numerator has a degree higher than that of the denominator, there is
no horizontal asymptote, but it may have an oblique asymptote instead.
• If the degree of the numerator is equal to the degree of the denominator, the
horizontal asymptote is at the -value equal to the ratio of the leading
coefficients of the numerator and the denominator.
• If the degree of the numerator is less than the degree of the denominator, the
horizontal asymptote is .
4

62. horizontal asymptote of a rational function
determined by comparing the degree of the polynomials in the numerator and
denominator
4
Example:
The numerator and denominator of the function are the
same and
Thus, the horizontal asymptote is the line .

63. Steps in Graphing a Rational Function
• Modify the expression algebraically and rewrite in the form .
• Solve for the intercepts.
• Find the asymptotes.
• Observe the behavior of the function using tables of values.
• Sketch the graph of the function.
5

64. Example 1: Graph the rational function .

65. Example 1: Graph the rational function .
Solution:
The function is already in the form so we just leave it as it is.

66. Example 1: Graph the rational function .
Solution:
The numerator is zero when .
The denominator when .
Since the numerator and denominator have no common
zero, then the -intercept is the point . Note that this point is
also the -intercept because when , .

67. Example 1: Graph the rational function .
Solution:
The denominator when , so there is a vertical asymptote at .
Since the numerator and the denominator have the same degree, we
just divide the coefficients of the leading terms. The coefficient of the
leading term in the numerator is 1 while the leading term in the
denominator is 1. Thus, there is a horizontal asymptote at .

68. Example 1: Graph the rational function .
Solution:
Let us check the behavior of the graph near the vertical
asymptote.
As approaches from the left, the
value of decreases without
bound.

69. Example 1: Graph the rational function .
Solution:
Let us check the behavior of the graph near the vertical
asymptote.
As approaches from the right,
the value of increases without
bound.

70. Example 1: Graph the rational function .
Solution:
Let us also check the behavior of the graph near the intercept .

71. Example 1: Graph the rational function .
Solution:
The graph of is:

72. Example 2: Graph the rational function .

73. Example 2: Graph the rational function .
Solution:
The function is already in the form so we just leave it as it is.

74. Example 2: Graph the rational function .
Solution:
The numerator is never zero; thus there is no -intercept.
When , is equal to .
So, the -intercept is at the point

75. Example 2: Graph the rational function .
Solution:
The denominator and and , so the lines and are vertical
asymptotes.
Since the degree of the denominator is greater than the
numerator, the -axis is the horizontal asymptote.

76. Example 2: Graph the rational function.
Solution:
We then check the behavior of the graph near the vertical
asymptotes.
As approaches from the left, the
value of increases without
bound.

77. Example 2: Graph the rational function.
Solution:
We then check the behavior of the graph near the vertical
asymptotes.
As approaches from the right,
the value of decreases without
bound.

78. Example 2: Graph the rational function .
Solution:
Let us also check the behavior of the graph near the vertical
asymptote .
As approaches from the left, the
value of decreases without
bound.

79. Example 2: Graph the rational function .
Solution:
Let us also check the behavior of the graph near the vertical
asymptote .
As approaches from the right,
the value of increases without
bound.

80. Example 2: Graph the rational function .
Solution:
Let us also check the behavior of the graph near the intercept .

81. Example 2: Graph the rational function .
Solution:
The graph of is:

82. Individual Practice:
1. Graph the rational function .
2. Graph the rational function .

83. -intercept(s) of a rational function
-value(s) that make the numerator zero but are not zeros of the denominator
1
-intercept of a rational function
obtained by evaluating the function at
2
vertical asymptote(s) of a rational function
-value(s) that make the denominator zero but are not zeros of the numerator
3
horizontal asymptote of a rational function
determined by comparing the degree of the polynomials in the numerator and
denominator
4

84. Steps in Graphing a Rational Function
• Modify the expression algebraically and rewrite in the form .
• Solve for the intercepts.
• Find the asymptotes.
• Observe the behavior of the function using tables of values.
• Sketch the graph of the function.
5

85. Solving Problems Involving
Rational Functions

86. ● How can you write a rational function to represent a
situation, and what does that function mean?
● How can you solve real-world problems involving
rational functions algebraically and graphically?

87. Using the graph below, find the values of at
. Construct a table of values.

88. Guidelines in Solving Problems Involving Rational
Functions
• Carefully read the problem and identify what is asked and the given
information.
• Identify what concepts may be needed to solve the problem.
• Define the variables you will be using to solve the problem and write an
equation that involves the unknown.
• Systematically perform mathematical processes until the value of the
unknowns are obtained.
1

89. Guidelines in Solving Problems Involving Rational
Functions
1
Example:
The average cost of an item is calculated by dividing the
total cost by the number of items . If the total cost is given by
write a rational function that gives the average cost of an
item.

90. Guidelines in Solving Problems Involving Rational
Functions
1
Identify what is asked and what are given.
We are asked to write a rational function for the average cost of an
item.
It is given that the total cost is . It is also given that to find the average
cost, the total cost must be divided by the number of items .

91. Guidelines in Solving Problems Involving Rational
Functions
1
Identify the concept to be used.
We need the concept of rational functions to answer this
problem.
A rational function is in the form , where .

92. Guidelines in Solving Problems Involving Rational
Functions
1
Solve for or find what is asked.
Since it is given that the average cost is simply the total cost divided by the total
number of items, we may form the average cost function by writing a rational
function , where is the total cost function and is the function representing the
number of units.
Thus, the average cost function is given by .

93. Example 1:
Suppose that a pharmaceutical company spent ₱500 000 to
develop a new skin lightening pill, plus ₱5 each to make the
pills. If the total cost is given by , write a rational function
that gives the average cost per pill.

94. Solution:
1. Identify what is asked and what are given.
We are asked to write a rational function for the
average cost per pill.
It is given that the total cost is . To find the average cost,
the total cost must be divided by the number of pills .

95. Solution:
2. Identify the concept to be used.
We will need the concept of rational functions to answer
this problem.
A rational function is in the form , where .

96. Solution:
3. Solve for or find what is asked.
Since the average cost is simply the total cost divided by
the total number of pills, we may form the average cost
function by writing a rational function , where is the
total cost function and is the function representing
the number of units.

97. Solution:
3. Solve for or find what is asked.
Thus, the average cost function is given by
.

98. Example 2:
Using the average cost function obtained in Example 1, solve
for the following:
a. the average cost per pill when 50 000 pills are made
b. the value of that results in an average cost of ₱25

99. Solution:
1. Identify what is asked and what are given.
We are asked to find the average cost when 50 000 pills
are made, and the value of or the number of pills that
results in an average cost of ₱25.

100. Solution:
2. Find the average cost for .
We need to find for .
Substituting this value into the average cost function.

101. Solution:
2. Find the average cost for .

102. Solution:
2. Find the average cost for .
Thus, the average cost when is ₱15.

103. Solution:
3. Find the number of pills that corresponds to an average
cost of ₱25.
To do this, we simply have to look for the -value that
corresponds to an value of 25.
Substituting this value into the function.

104. Solution:
3. Find the number of pills that corresponds to an average
cost of ₱25.

105. Solution:
3. Find the number of pills that corresponds to an average
cost of ₱25.
Therefore, the number of pills that have an average cost
of ₱25 is 25 000.

106. Individual Practice:
1. The membership fee for a holiday raffle draw costs ₱2
500 and each ticket is sold at ₱150. Write a rational
function that gives the average cost per ticket if the total
cost is , where is the number of tickets.

107. Individual Practice:
2. Refer to the average cost per ticket you obtained in
Problem 1. Find the average cost per ticket if you buy 20
tickets. Also, find the maximum number of tickets you can
buy if the average cost per ticket is not to exceed ₱200.

108. Group Practice: Form 6 groups of students.
Margie and Kenneth went for a hike. They started from the
same place at the same time towards Laguna which is
110 km away from their place. Kenneth traveled at 50 kph
and reached Laguna 1 hour before Margie.
Find the rate of Margie.

109. Guidelines in Solving Problems Involving Rational
Functions
• Carefully read the problem and identify what is asked and the given
information.
• Identify what concepts may be needed to solve the problem.
• Define the variables you will be using to solve the problem and write an
equation that involves the unknown.
• Systematically perform mathematical processes until the value of the
unknowns are obtained.
1