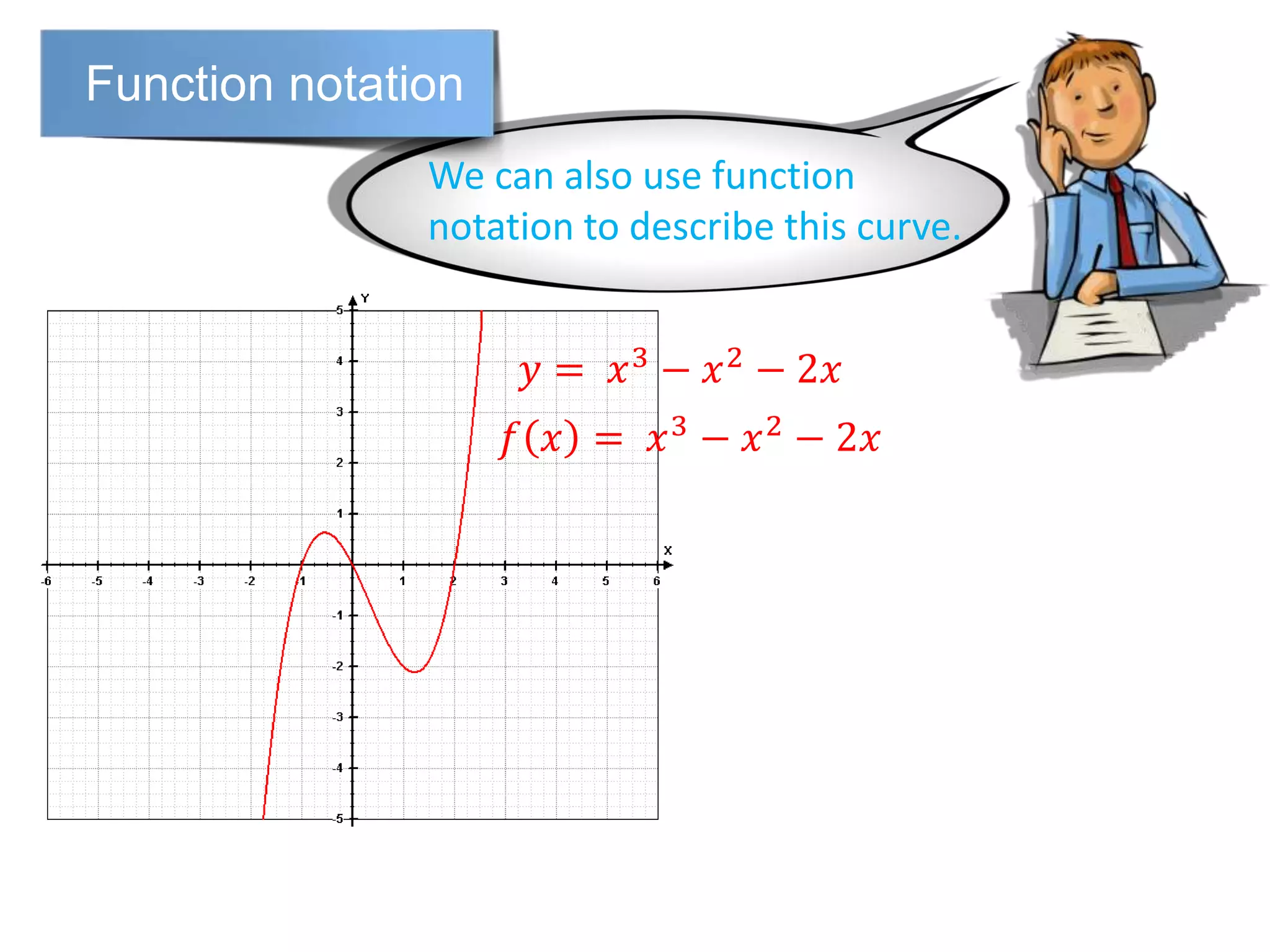
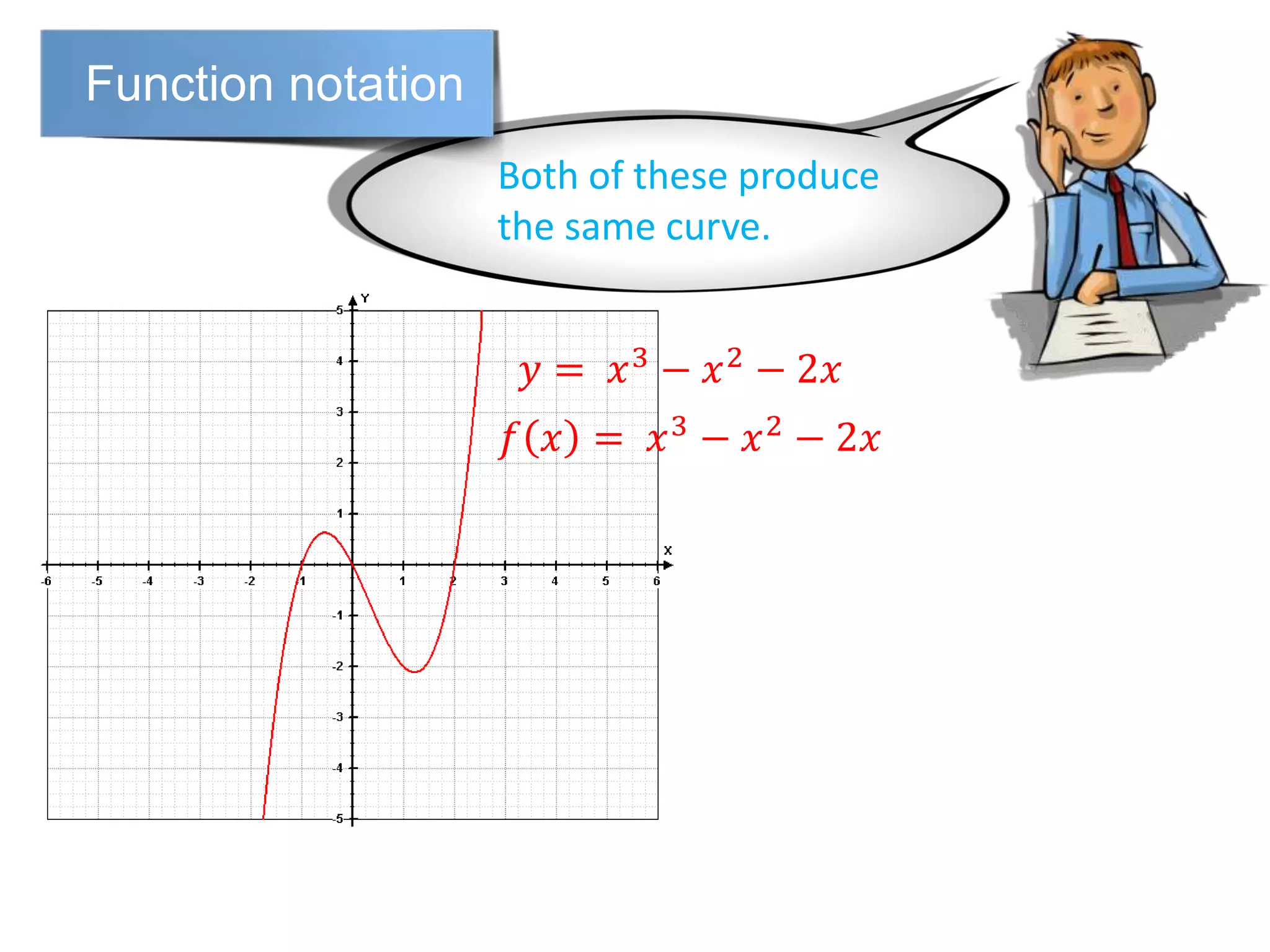
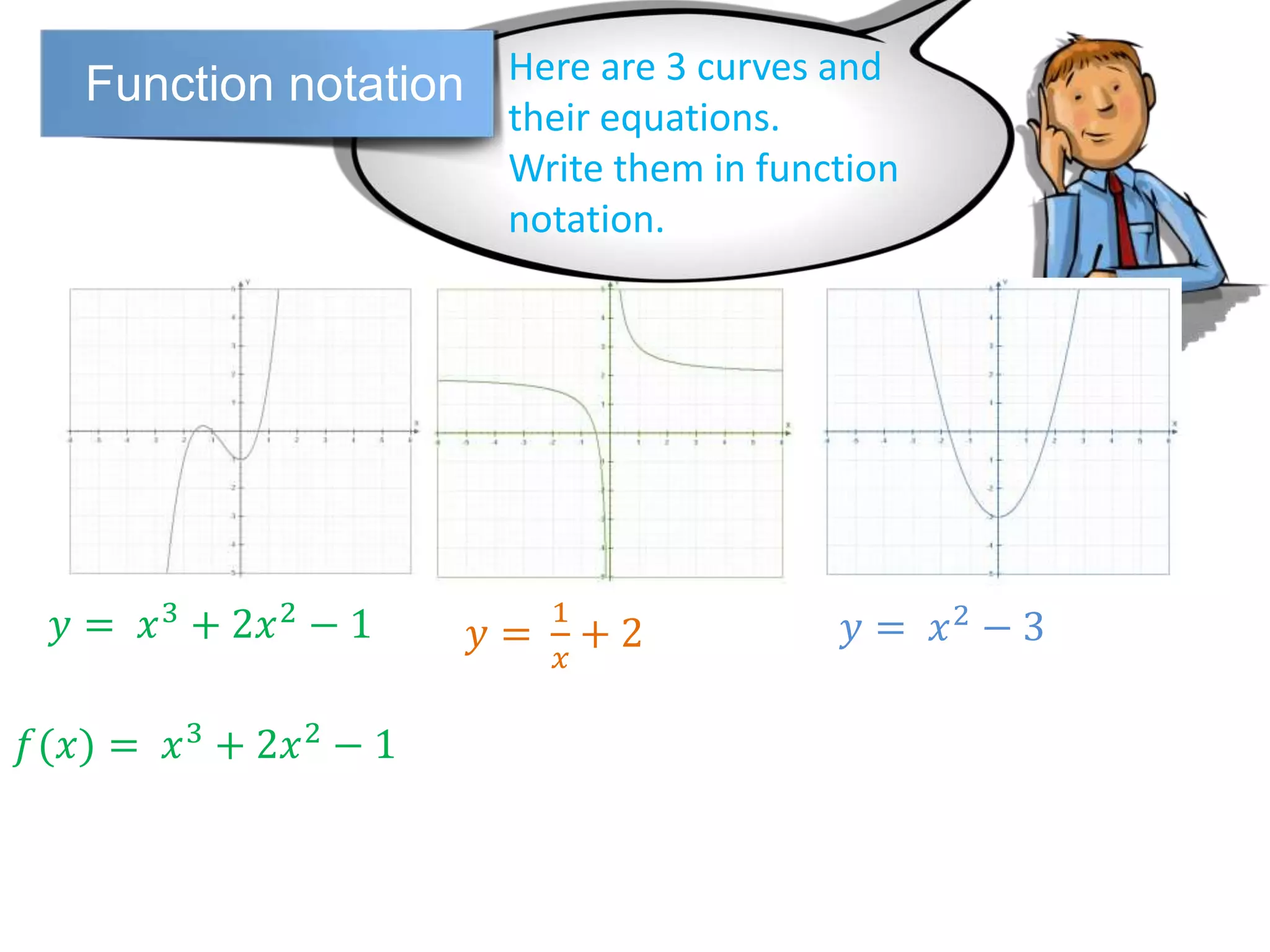
The document discusses function notation and transformations of functions. It provides examples of writing quadratic, cubic, and rational functions in function notation. It also demonstrates how functions are translated vertically by adding or subtracting a number from the original function. Translating a function f(x) by a results in the new function f(x)+a or f(x)-a.

1. How are graphs
transformed by
f(x)+a and
f(x+a)?

2. Use function
notation to
describe a
curve
Recognise
translations
of quadratic
functions.

3. Function notation
This is the graph of a cubic.
𝑦 = 𝑥3 − 𝑥2 − 2𝑥

4. Function notation
We can also use function
notation to describe this curve.
𝑦 = 𝑥3 − 𝑥2 − 2𝑥
𝑓 𝑥 = 𝑥3 − 𝑥2 − 2𝑥

5. Function notation
Both of these produce
the same curve.
𝑦 = 𝑥3 − 𝑥2 − 2𝑥
𝑓 𝑥 = 𝑥3 − 𝑥2 − 2𝑥

6. Function notation Here are 3 curves and
their equations.
Write them in function
notation.
𝑦 = 𝑥3 + 2𝑥2 − 1 𝑦 = 𝑥2 − 3
𝑦 =
1
𝑥
+ 2

7. Function notation Here are 3 curves and
their equations.
Write them in function
notation.
𝑦 = 𝑥3 + 2𝑥2 − 1 𝑦 = 𝑥2 − 3
𝑦 =
1
𝑥
+ 2
𝑓(𝑥) = 𝑥3
+ 2𝑥2
− 1

8. Function notation Here are 3 curves and
their equations.
Write them in function
notation.
𝑦 = 𝑥3 + 2𝑥2 − 1 𝑦 = 𝑥2 − 3
𝑦 =
1
𝑥
+ 2
𝑓(𝑥) = 𝑥3
+ 2𝑥2
− 1 𝑓(𝑥) =
1
𝑥
+ 2

9. Function notation Here are 3 curves and
their equations.
Write them in function
notation.
𝑦 = 𝑥3 + 2𝑥2 − 1 𝑦 = 𝑥2 − 3
𝑦 =
1
𝑥
+ 2
𝑓(𝑥) = 𝑥3
+ 2𝑥2
− 1 𝑓(𝑥) =
1
𝑥
+ 2 𝑓 𝑥 = 𝑥2 − 3

10. Function notation
We can also describe
function in words:
𝑓 𝑥 = 𝑥2
− 3 “f of 𝑥 is 𝑥 squared subtract 3.”

11. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Function notation
makes it clear what we
are substituting :

12. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Function notation
makes it clear what we
are substituting :

13. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Find the values for the
others.
𝑓 0 = (0)2− 3 = ?
𝑓 −1 = ( ? )2
− 3 = ?
𝑓 10 = ( ? )2− 3 = ?
𝑓 90 = ( ? )2
− 3 = ?

14. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Find the values for the
others.
𝑓 0 = (0)2− 3 = -3
𝑓 −1 = ( ? )2
− 3 = ?
𝑓 10 = ( ? )2− 3 = ?
𝑓 90 = ( ? )2
− 3 = ?

15. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Find the values for the
others.
𝑓 0 = (0)2− 3 = -3
𝑓 −1 = (−1)2
− 3 = -2
𝑓 10 = ( ? )2− 3 = ?
𝑓 90 = ( ? )2
− 3 = ?

16. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Find the values for the
others.
𝑓 0 = (0)2− 3 = -3
𝑓 −1 = (−1)2
− 3 = -2
𝑓 10 = (10)2− 3 = 97
𝑓 90 = ( ? )2
− 3 = ?

17. Function notation
𝑓 𝑥 = 𝑥2
− 3
𝑓 1 = (1)2− 3 = -2
𝑓 2 = (2)2− 3 = 1
“f of 𝑥 is square and subtract 3.”
Find the values for the
others.
𝑓 0 = (0)2− 3 = -3
𝑓 −1 = (−1)2
− 3 = -2
𝑓 10 = (10)2− 3 = 97
𝑓 90 = ( 90)2
− 3 = 8097

18. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚

19. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10

20. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4

21. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1

22. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17

23. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17 = 17

24. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17 = 17 = -8

25. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17 = 17 = -8
= 0

26. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17 = 17 = -8
= 0 = 0.5

27. Function notation
1. When 𝑓 𝑥 = 3𝑥 + 4, evaluate
𝑓 2 𝑓 0 𝑓 −1
2. When 𝑔 𝑝 = 𝑝2
− 8, evaluate
𝑔 5 𝑔 −5 𝑔 0
3. When ℎ 𝑚 = sin m, evaluate
ℎ 0˚ ℎ 30˚ ℎ −90˚
= 10 = 4 = 1
= 17 = 17 = -8
= 0 = 0.5 = -1

28. Combining functions
Given that f(𝒙) = 𝒙𝟐
Let 𝒚 = f(𝒙) + 2
What is 𝒚 if 𝒙 = 4?
Function notation

29. Translating functions
Given that f(𝒙) = 𝒙𝟐
𝒚 = f(𝟒) + 2 = (𝟒)𝟐 + 2 = 18
Let 𝒚 = f(𝒙) + 2
What is 𝒚 if 𝒙 = 4?
Function notation

30. Translating functions
Given that f(𝒙) = 𝒙𝟐
𝒚 = f(𝟒) + 2 = (𝟒)𝟐 + 2 = 18
Let 𝒚 = f(𝒙) + 2
What is 𝒚 if 𝒙 = 4?
Now let 𝒚 = f(𝒙 + 𝟐)
What is 𝒚 if 𝒙 = 4?
Function notation

31. Translating functions
Given that f(𝒙) = 𝒙𝟐
𝒚 = f(𝟒) + 2 = (𝟒)𝟐 + 2 = 18
Let 𝒚 = f(𝒙) + 2
What is 𝒚 if 𝒙 = 4?
Now let 𝒚 = f(𝒙 + 𝟐)
What is 𝒚 if 𝒙 = 4?
𝒚 = f(𝟒 + 𝟐) = (𝟔)𝟐 = 36
Function notation

32. Translating functions
Given that f(𝒙) = 𝒙𝟐
𝒚 = f(𝟒) + 2 = (𝟒)𝟐 + 2 = 18
Let 𝒚 = f(𝒙) + 2
What is 𝒚 if 𝒙 = 4?
Now let 𝒚 = f(𝒙 + 𝟐)
What is 𝒚 if 𝒙 = 4?
𝒚 = f(𝟒 + 𝟐) = (𝟔)𝟐 = 36
So, 𝑦 = f(𝒙 + 𝟐) ⇒ 𝑦 = (𝒙 + 𝟐)𝟐
Function notation

33. Use function
notation to
describe a
curve
Recognise
translations
of quadratic
functions.

34. Use function
notation to
describe a
curve
Recognise
translations
of quadratic
functions.

35. Quadratic functions
Here is y = 𝑥2

36. Quadratic functions
Which
transformation
would map the red
curve on to the blue
one?

37. Quadratic functions
Translation
up 3 units
or by 0
3
Translation by 0
3

38. 6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
5
4
3
2
1
-1
-2
-3
-4
-5
X
Y
Quadratic functions
Which
transformation
would map the red
curve on to the
green one?
Translation by 0
3

39. 6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
5
4
3
2
1
-1
-2
-3
-4
-5
X
Y
Quadratic functions
Translation
down 2 units
or by 0
−2
Translation by 0
−2
Translation by 0
3

40. 6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
5
4
3
2
1
-1
-2
-3
-4
-5
X
Y
Quadratic functions
Now look at the
function statement
for each curve.
What do you notice?
y = 𝒙𝟐
y = 𝑥2 + 3
y = 𝑥2 - 2
Translation by 0
3
Translation by 0
−2

41. 6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
5
4
3
2
1
-1
-2
-3
-4
-5
X
Y
Quadratic functions
Adding or
subtracting a number
translates the quadratic
curve up or down
by that number
of units.
Translation by 0
3
Translation by 0
−2
y = 𝑥2 + 3
y = 𝒙𝟐
y = 𝑥2 - 2

42. Quadratic functions
This is y = −𝑥2
y = −𝒙𝟐

43. Quadratic functions
This is y = −𝑥2
y = −𝒙𝟐
It cuts the y axis at (0,0).
What would y = −𝑥2+ 2
look like and where
would it cut
the y axis?

44. Quadratic functions
It cuts the y axis
at (0,2).
It is a translation by 0
2
y = −𝒙𝟐
y = −𝒙𝟐 + 2

45. Quadratic functions
It cuts the y axis
at (0,2).
It is a translation by 0
2
What would produce a
translation by 0
−3
y = −𝒙𝟐 + 2
y = −𝒙𝟐

46. Quadratic functions
What would produce a
translation by 0
−3
y = −𝒙𝟐 - 3
y = −𝒙𝟐
y = −𝒙𝟐 - 3

47. Quadratic functions
How would you
describe these
transformations
of the red curve?

48. Quadratic functions
Translations by:
2
0
−3
0
4
0
−5
0

49. Quadratic functions
Now compare with
the equations.
2
0
−3
0
4
0
−5
0
y = 𝒙𝟐
y = (𝒙 − 𝟐)𝟐
y = (𝒙 − 𝟒)𝟐
y = (𝒙 + 𝟑)𝟐
y = (𝒙 + 𝟓)𝟐
What do you
notice?

50. Quadratic functions
Units moved is the
same as the number
in the bracket
but the sign is
opposite.
2
0
−3
0
4
0
−5
0
y = 𝒙𝟐
y = (𝒙 − 𝟐)𝟐
y = (𝒙 − 𝟒)𝟐
y = (𝒙 + 𝟑)𝟐
y = (𝒙 + 𝟓)𝟐

51. Quadratic functions
Where would
y = (𝒙 − 𝟏)𝟐 be?
y = 𝒙𝟐

52. Quadratic functions
y = 𝒙𝟐

53. Quadratic functions
And
y = (𝒙 + 𝟏)𝟐?
y = (𝒙 − 𝟏)𝟐
y = 𝒙𝟐

54. Quadratic functions
y = (𝒙 − 𝟏)𝟐
y = 𝒙𝟐
y = (𝒙 + 𝟏)𝟐

55. Quadratic functions
Transformations of y = 𝒙𝟐
Equation Transformation Comment
y = 𝒙𝟐 + a Translation by
𝑎
0
Translate in y direction.
Up if a positive.
Down if a negative.
The same as you see.
y = (𝒙 + 𝒂)𝟐
Translation by
0
−𝑎
Translate in x direction.
Left if a positive.
Right if a negative.
The opposite to what you see.

56. Quadratic functions
1. 2.
3. 4.
What are the
equations of
these curves?

57. Quadratic functions
1. 2.
3. 4.
What are the
equations of
these curves?
y = (𝒙 − 𝟏)𝟐

58. Quadratic functions
1. 2.
3. 4.
What are the
equations of
these curves?
y = (𝒙 − 𝟏)𝟐 y = (𝒙 + 𝟏)𝟐

59. Quadratic functions
1. 2.
3. 4.
What are the
equations of
these curves?
y = (𝒙 − 𝟏)𝟐 y = (𝒙 + 𝟏)𝟐
y = 𝒙𝟐 -1

60. Quadratic functions
1. 2.
3. 4.
What are the
equations of
these curves?
y = (𝒙 − 𝟏)𝟐 y = (𝒙 + 𝟏)𝟐
y = 𝒙𝟐 -1 y = 𝒙𝟐
+2

61. Translating functions
Equation Transformation Comment
y = f(𝒙)+ a Translation by
𝑎
0
Translate in y direction.
Up if a positive.
Down if a negative.
The same as you see.
y = f(𝒙 + 𝒂) Translation by
0
−𝑎
Translate in x direction.
Left if a positive.
Right if a negative.
The opposite to what you see.
Transformations of y = f(𝒙)

62. Use function
notation to
describe a
curve
Recognise
translations
of quadratic
functions.

63. Use function
notation to
describe a
curve
Recognise
translations
of quadratic
functions.

64. How are graphs
transformed by
f(x)+a and f(x+a)
?
Visit: https://tute.in/