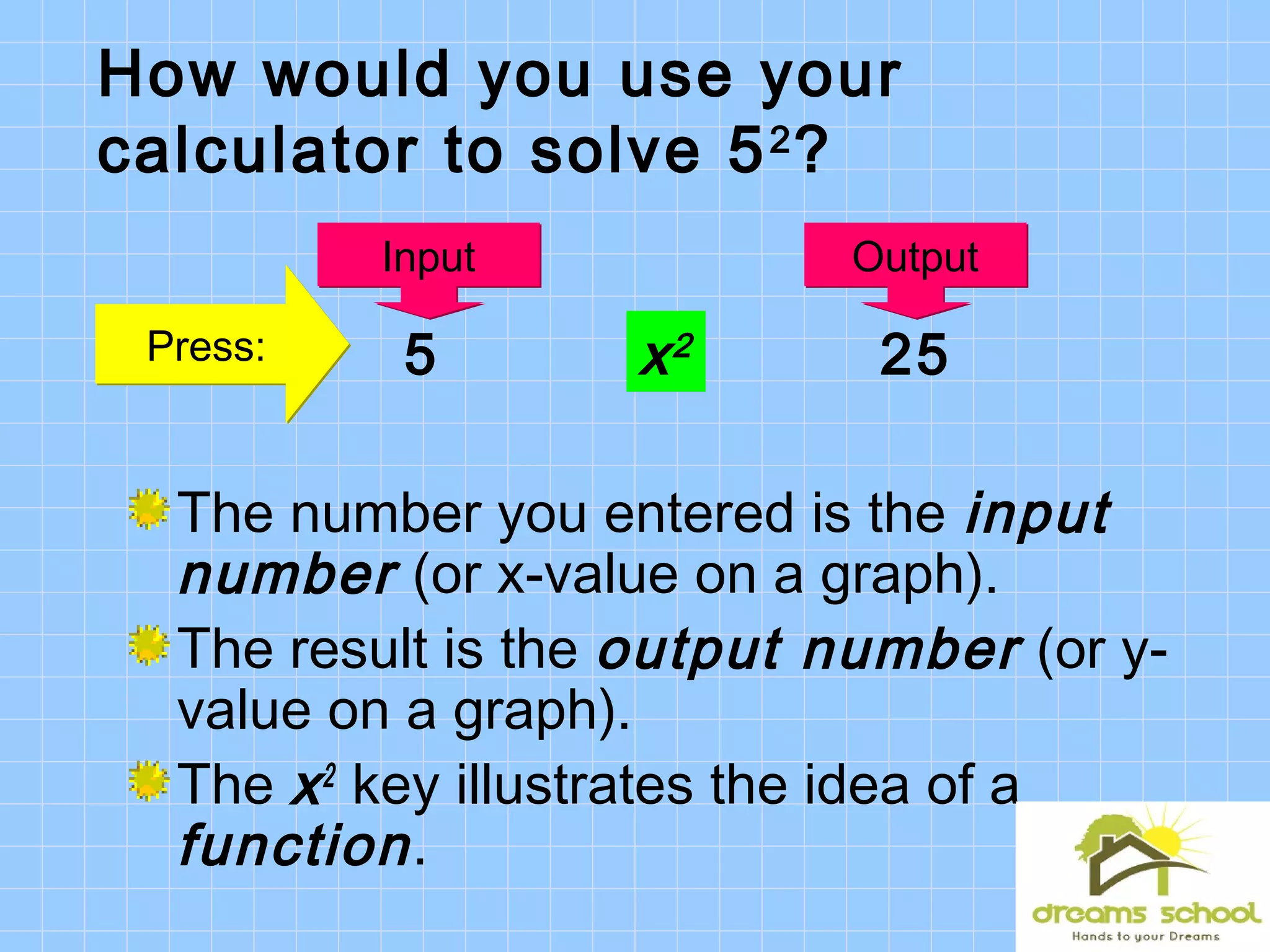
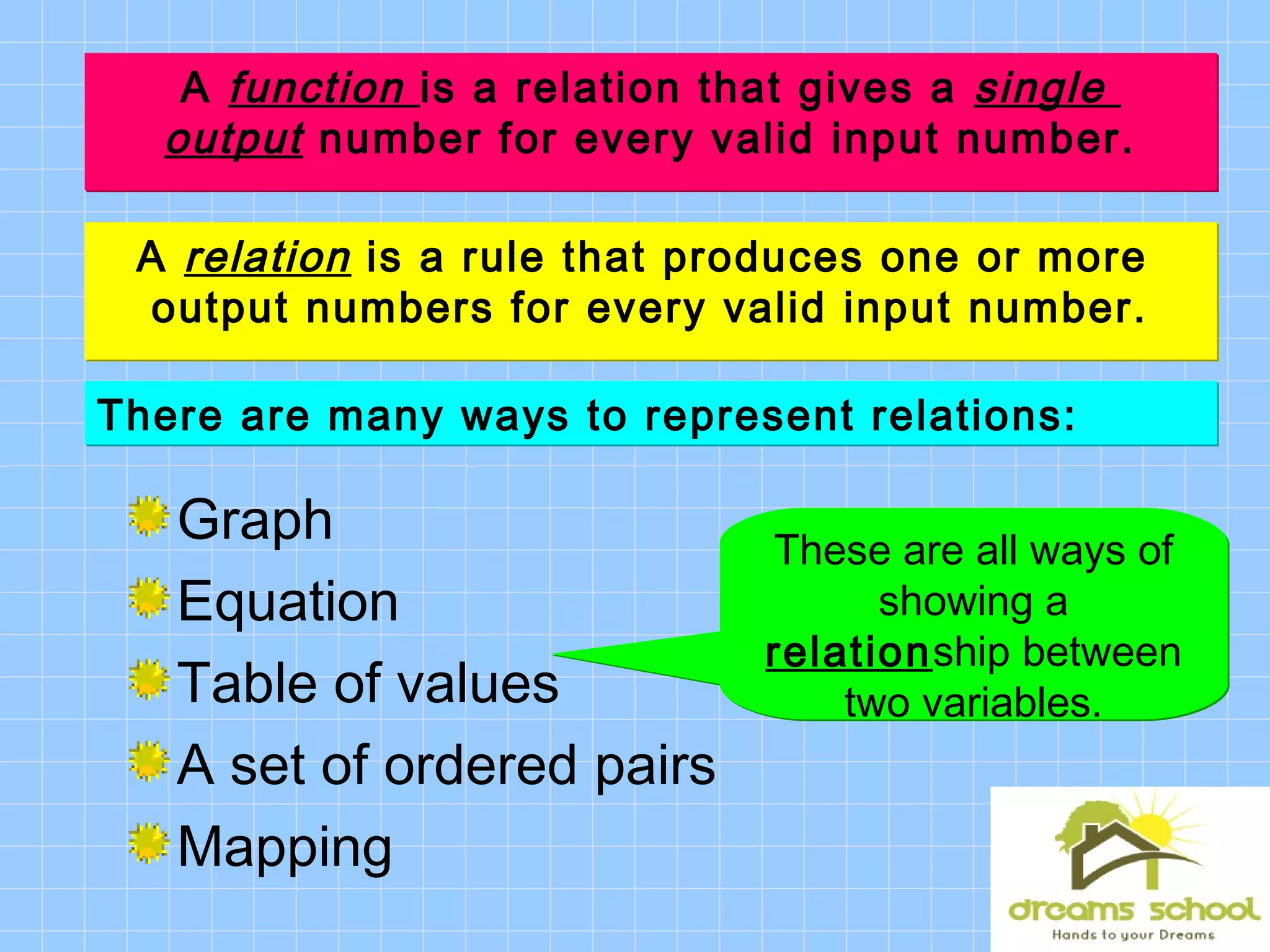
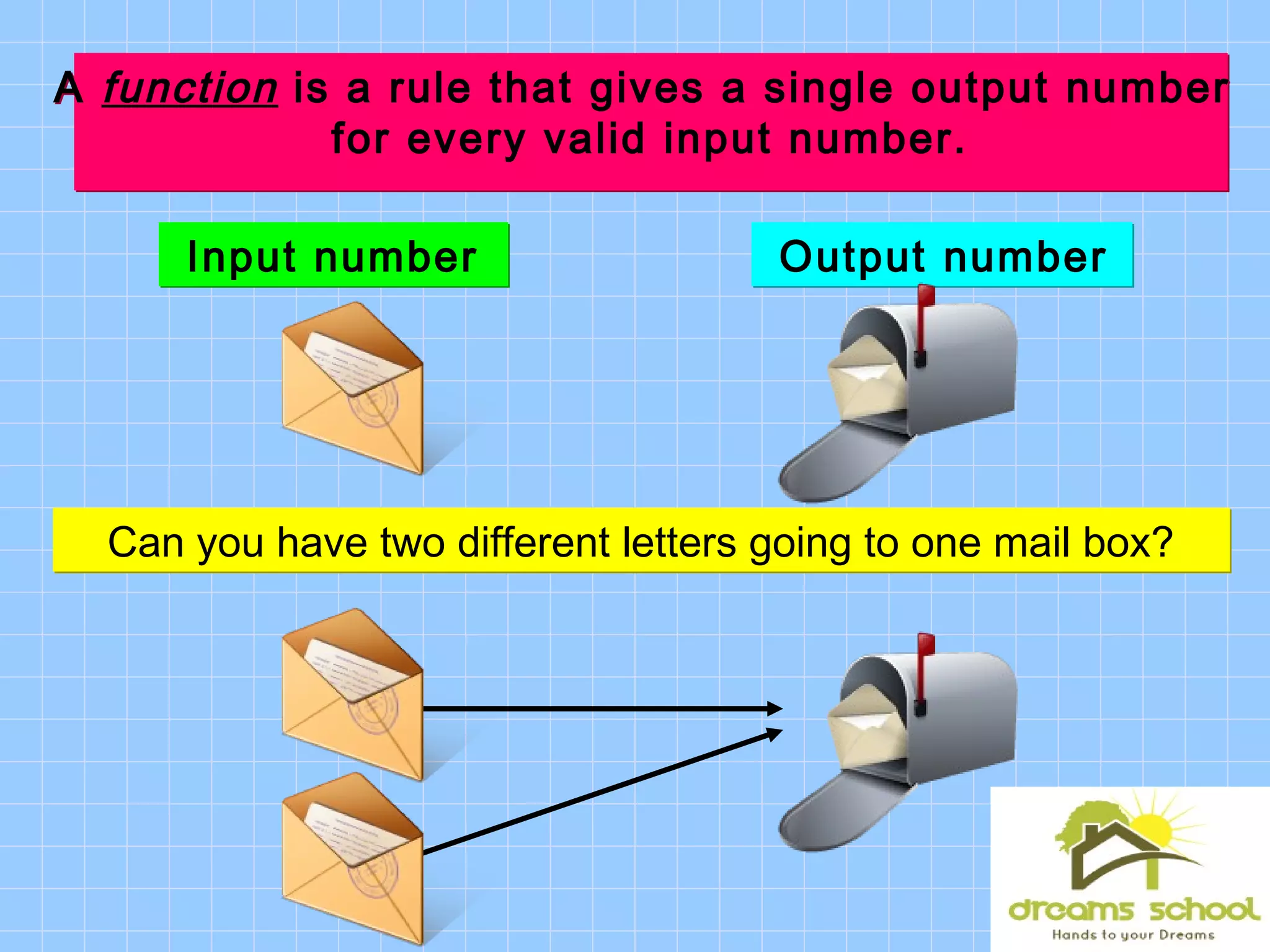
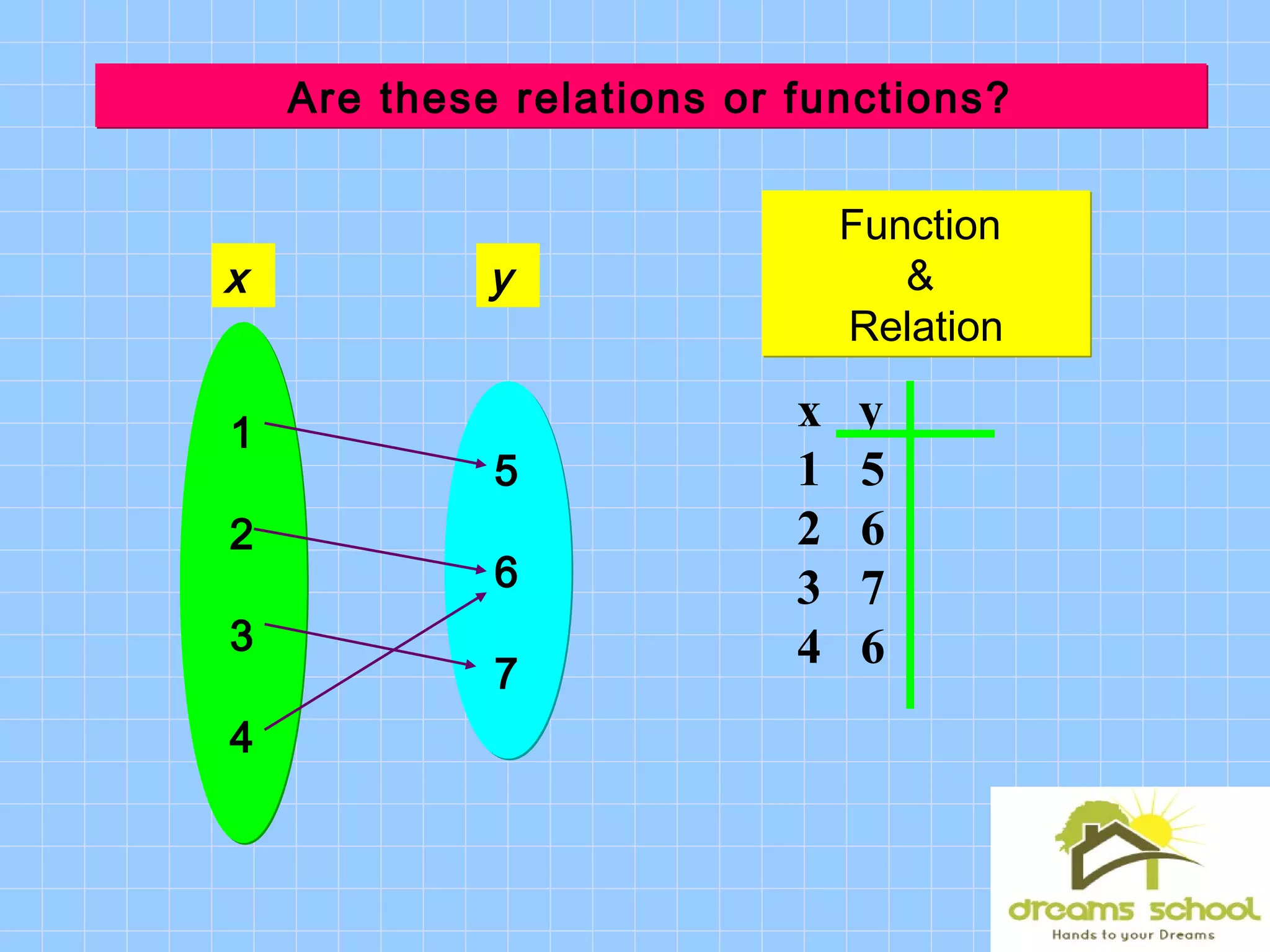
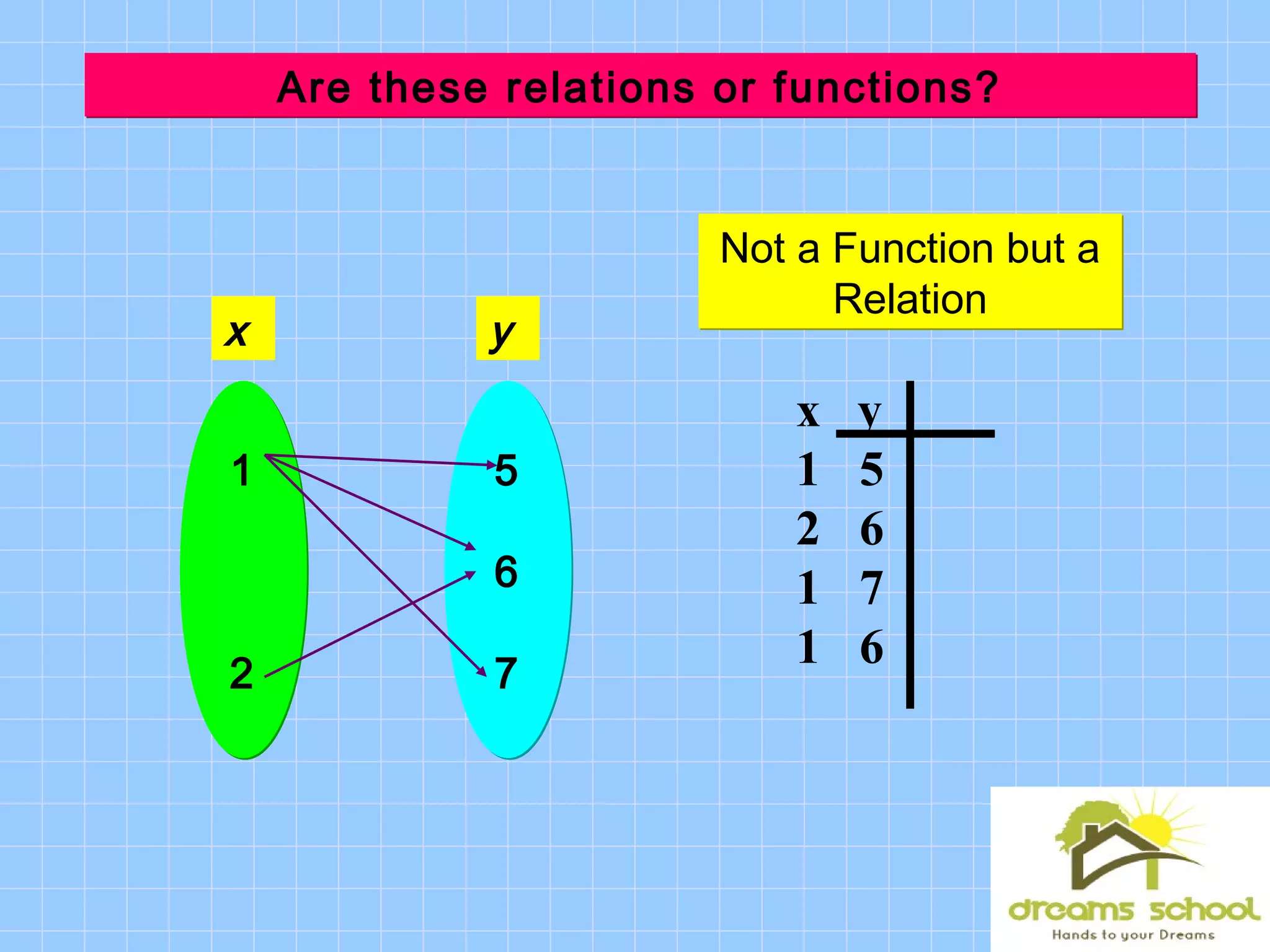
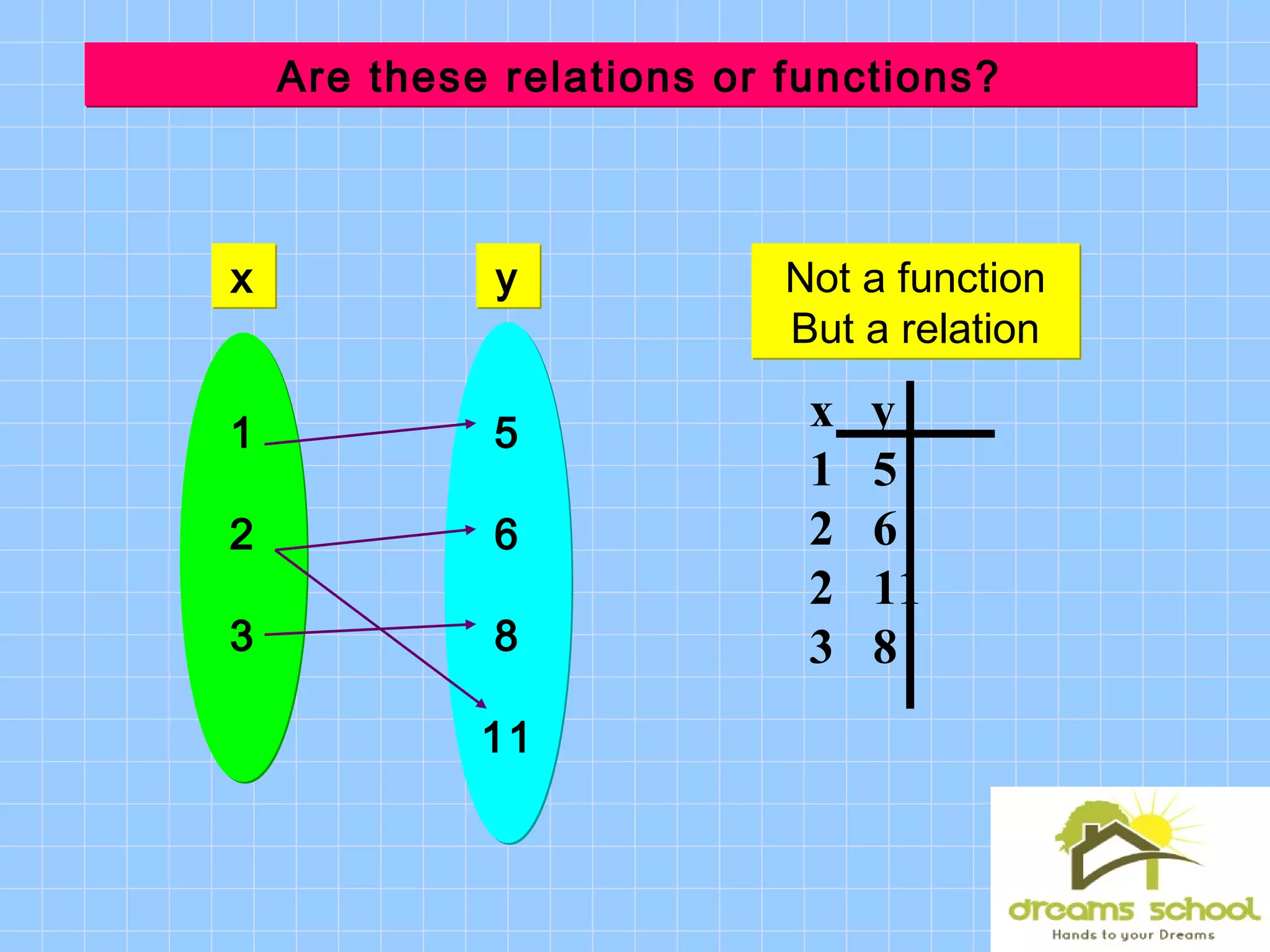
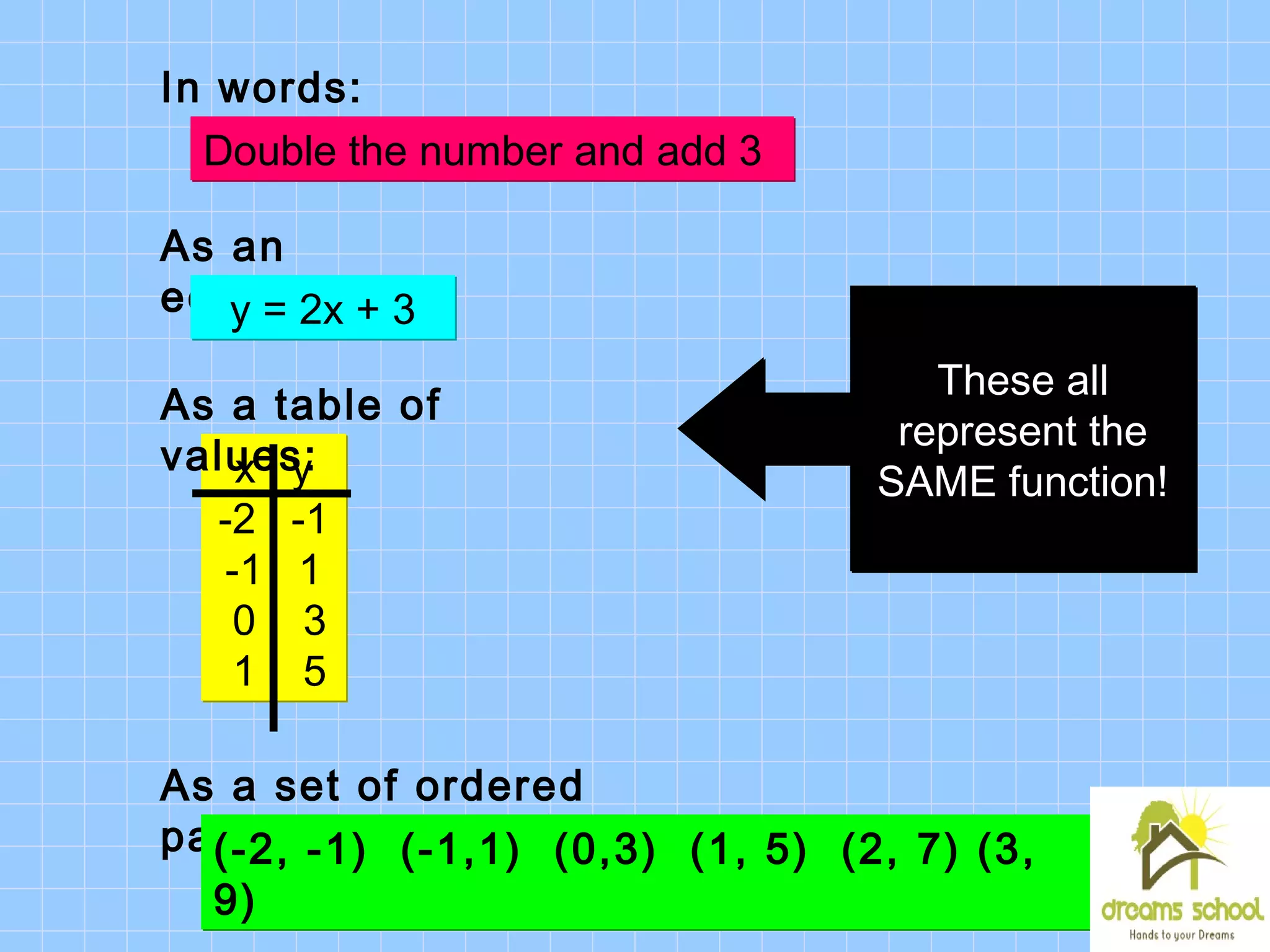
This document discusses functions and functional notation. It defines a function as a rule that assigns a single output value to each input value. It provides examples of relations and functions using tables, ordered pairs, and equations. It also introduces functional notation to represent functions, where f(x) means the output of the function f when the input is x. The document evaluates example functions using this notation and combines multiple functions.

1. 1

3. 5 x2 25
How would you use your
calculator to solve 52
?
The number you entered is the input
number (or x-value on a graph).
The result is the output number (or y-
value on a graph).
The x2
key illustrates the idea of a
function.
InputInput OutputOutput
Press:Press:

4. A function is a relation that gives a single
output number for every valid input number.
A function is a relation that gives a single
output number for every valid input number.
There are many ways to represent relations:There are many ways to represent relations:
A relation is a rule that produces one or more
output numbers for every valid input number.
A relation is a rule that produces one or more
output numbers for every valid input number.
These are all ways of
showing a
relationship between
two variables.
These are all ways of
showing a
relationship between
two variables.
Graph
Equation
Table of values
A set of ordered pairs
Mapping

5. A function is a rule that gives a single output number
for every valid input number.
A function is a rule that gives a single output number
for every valid input number.
To help remember & understand the definition:
Think of your input number, usually your
x-coordinate, as a letter.
Think of your input number, usually your
x-coordinate, as a letter.
Think of your output number, usually your
y-coordinate, as a mailbox.
Think of your output number, usually your
y-coordinate, as a mailbox.

6. A function is a rule that gives a single output number
for every valid input number.
A function is a rule that gives a single output number
for every valid input number.
Input numberInput number Output numberOutput number
Can you have one letter going to two different mail boxes?Can you have one letter going to two different mail boxes?
Not a FUNCTIONNot a FUNCTION

7. A function is a rule that gives a single output number
for every valid input number.
A function is a rule that gives a single output number
for every valid input number.
Input numberInput number Output numberOutput number
Can you have two different letters going to one mail box?Can you have two different letters going to one mail box?

8. Are these relations or functions?Are these relations or functions?
x y
x y
1 5
2 6
3 7
4 6
1
2
3
4
1
2
3
4
5
6
7
5
6
7
Function
&
Relation
Function
&
Relation

9. Are these relations or functions?Are these relations or functions?
x y
x y
1 5
2 6
1 7
1 6
1
2
1
2
5
6
7
5
6
7
Not a Function but a
Relation
Not a Function but a
Relation

10. xx yy
x y
1 5
2 6
2 11
3 8
1
2
3
1
2
3
5
6
8
11
5
6
8
11
Not a function
But a relation
Not a function
But a relation
Are these relations or functions?Are these relations or functions?

11. x y
-2 -1
-1 1
0 3
1 5
x y
-2 -1
-1 1
0 3
1 5
Double the number and add 3Double the number and add 3
As an
equation:
In words:
y = 2x + 3y = 2x + 3
As a table of
values:
As a set of ordered
pairs:(-2, -1) (-1,1) (0,3) (1, 5) (2, 7) (3,
9)
(-2, -1) (-1,1) (0,3) (1, 5) (2, 7) (3,
9)
These all
represent the
SAME function!
These all
represent the
SAME function!

12. Lesson 5.2 (PART 2)
Math 10C

13. Functional Notation
An equation that is a function
may be expressed using
functional notation.
The notation f(x) (read “f of (x)”)
represents the variable y.

14. Example:
y = 2x + 6 can be written as f(x) = 2x + 6.
Given the equation y = 2x + 6, evaluate when x = 3.
y = 2(3) + 6
y = 12
Functional Notation Cont’d

15. For the function f(x) = 2x + 6, the notation f(3) means
that the variable x is replaced with the value of 3.
f(x) = 2x + 6
f(3) = 2(3) + 6
f(3) = 12
Functional Notation Con’t

16. Given f(x) = 4x + 8, find each:
1. f(2)
2. f(a +1)
3. f(−4a)
Evaluating Functions
= 4(2) + 8
= 16
= 4(a + 1) + 8
= 4a + 4 + 8
= 4a + 12
= 4(-4a) + 8
= -16a+ 8

17. If f(x) = 3x − 1, and g(x) = 5x + 3, find each:
Evaluating More Functions
= [3(2) -1] + [5(3) + 3]
= 6 - 1 + 15 + 3
= 23
= [3(4) - 1] - [5(-2) + 3]
= 11 - (-7)
= 18
= 3[3(1) - 1] + 2[5(2) + 3]
= 6 + 26
= 32
1. f(2) + g(3)
2. f(4) - g(-2)
3. 3f(1) + 2g(2)

18. 18
Do you find this slides were useful?
One second of your life , can bring a smile in a girl life
If Yes ,Join Dreams School “Campaign for Female Education”
Help us in bringing a change in a girl life, because “When
someone takes away your pens you realize quite
how important education is”.
Just Click on any advertisement on the page, your one
click can make her smile.
Eliminate Inequality “Not Women”
One second of your life , can bring a smile in her life!!
Do you find these slides were useful?
If Yes ,Join Dreams School “Campaign
for Female Education”
Help us in bringing a change in a girl life,
because “When someone takes away
your pens you realize quite how
important education is”.
Just Click on any advertisement on the page,
your one click can make her smile.
We our doing our part & u ?
Eliminate Inequality “Not Women”