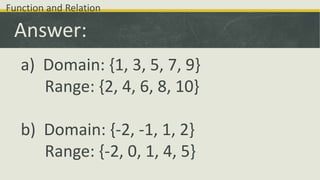
The document discusses functions and operations with functions. It defines a function as a relation where each input has a unique output. It introduces function notation using f(x) to represent the output of a function f given an input x. It then discusses how to evaluate functions using this notation. Finally, it discusses how functions can be combined using the basic operations of addition, subtraction, multiplication and division to create new functions.

1. Functions
Prepared by:
Arriesgado, Anna Marie M.
Pilapil, Maria Lindy M.
Rodrigo, Jailah Dale G.

2. Objectives
At the end of this lesson, I can:
•Determine the domain and range of a
function
•Use function notation and evaluate
functions
•Perform operations with functions

3. Functions
and
Relations

4. What is Function?
A function is a relation in
which each input has only
one output.
Functions and Relations

5. How about Relation?
A relation is a set of inputs
and outputs, often written
as ordered pairs (input,
output).
Function and Relation

6. There are two components in an
ordered pair. The set of all first
components of the ordered pairs is
called the domain of the relation, and
the set of all second components is
called the range.
Function and Relation

7. Example 1:
Function and Relation
Find the domain and range of the given relations.
a){(1,2) , (3,4) , (5,6) , (7,8) , 9,10)}
b){(-2,4) , (-1,1) , (-2,0) , (1,5) , (2,-2)}

8. Answer:
Function and Relation
a) Domain: {1, 3, 5, 7, 9}
Range: {2, 4, 6, 8, 10}
b) Domain: {-2, -1, 1, 2}
Range: {-2, 0, 1, 4, 5}

9. Example 2:
Function and Relation
Determine whether the given relation
represents a function.
Beth
Jovie
Mariz
Hubert
Richard
Banjo
a)

10. b) Beth
Jovie
Marivic
Joey
Glen
27
28
25
30
Function and Relation

11. Function and Relation
Answers:
a) The relation is a function because each
element in the domain corresponds to a
unique element in the range.
b) The relation is a function because each
element in the domain corresponds to a
unique element in the range.

12. Note:
Function and Relation
More than one element in the
domain can correspond to the same
element in the range but not the
range to the domain.

13. Function Notation

14. Function Notation
Functions are usually given
in terms of equation, rather
than sets of ordered pairs.
These equations are expressed
in a special notation.

15. Think of a function as a machine that
is programmed with a rule or an equation
that defines the relationship between
input and output. Consequently, the
machine gives the member of the range
(output).
Function Notation

16. Function Notation
As in the figure, the letter f is
used to name functions. The
input is represented by x and the
output by f(x). The special
notation f(x), read “f of x” or “f at
x”, represents the value of the
functions at x.

17. Example:
f(x) = 5x + 8
Find f(3).
Function Notation
Answer:
f(x) = 5x + 8
f(3) = 5(3) + 8
= 15 + 8
= 23

18. Note:
The function f(x) = 5x + 8 can also be expressed
as y = 5x + 8, replacing f(x) by y. The variable x is
called the independent variable because it can be
any of the permissible numbers from the domain.
The variable y is called the dependent variable
because its value depends on x.
Function Notation

19. Example 3:
For the function h defined by h(x) = 4x2 – x + 7,
evaluate:
a) h(0)
b) h(-3)
c) h(2)
Function Notation

20. Answers:
a)Substitute 0 for every x in h(x) and simplify.
h(0) = 4(0)2 – 0 + 7 = 4(0) + 7 =7
b)Substitute -3 for every x in h(x) and simplify.
h(-3) = 4(-3)2 – (-3) + 7 = 4(9) + 3 + 7 =46
c) Substitute 0 for every x in h(x) and simplify.
h(2) = 4(2)2 – 2 + 7 = 4(2) – 2 + 7 =21
Function Notation

21. Operations with
Functions

22. Just as two real numbers can be
combined by the operations of addition,
subtraction, multiplication and division to
form other real numbers, two functions
can be combined to create a new one.
Operations with Functions

23. For example: f(x) = x2 – 5x + 2 and g(x) = 2x + 7
f(x) + g(x) = (x2 – 5x + 2) + (2x + 7) = x2 – 3x + 9 Sum
f(x) - g(x) = (x2 – 5x + 2) - (2x + 7) = x2 – 7x – 5 Difference
f(x) * g(x) = (x2 – 5x + 2) * (2x + 7) Product
=2x3 – 3x2 – 31x + 14
f(x) / g(x) = (x2 – 5x + 2) / (2x + 7) =
𝑥2− 5𝑥 +2
2𝑥 +7
Quotient
Operations with Functions

24. Evaluation
Good luck and God Bless!!

25. I. Find the domain and range of the given relations and identify whether
the relation is function or just merely relation.
1. {(2, 1) , (12, 2) , (2, 8) , (3, 11) ,(11, 12)}
2. {(3, 77) , (5, 79) , (9, 83) , (12, 87) , (15, 90) , (16, 95)}
3. {(-2, 16) , (-4, 4) , (-3, 3) , (2, 12) , (-4, 0)}
4. {(-1, -5) , (0, 0) , (1, 3) , (2, 4) , (3, 3) , (4, 0) , (5, -5)}
5. {(2, 2), (3, 1) , (4, 0) , (5, 1) , (6, 2)}

26. II. For the function j defined by j(x) = 5x3 + 8x2 – 22, evaluate:
a)h(2)
b)h(-2)
c) h(7)
d)h(5)
e)h(-4)

27. III. Let f(x) = 2x2 -7 and g(x) = 3x + 10. Find the following:
a)(f + g ) (x) = f(x) + g(x)
b)(f - g ) (x) = f(x) - g(x)
c) (f * g ) (x) = f(x) * g(x)
d)(f / g ) (x) = f(x) / g(x)