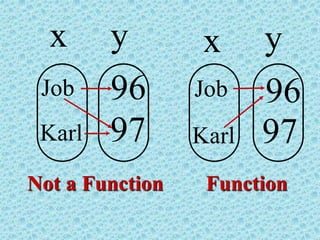
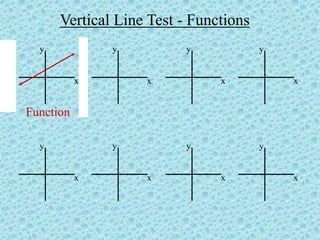
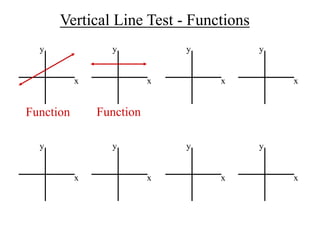
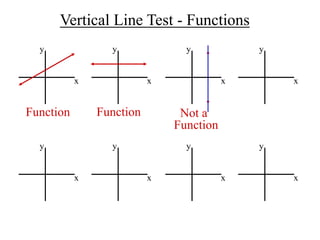
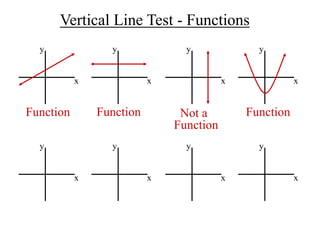
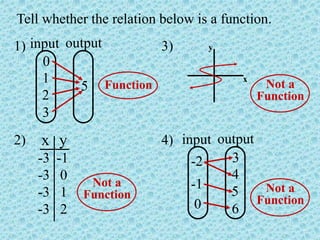
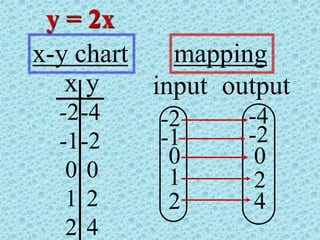
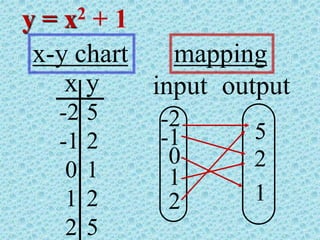
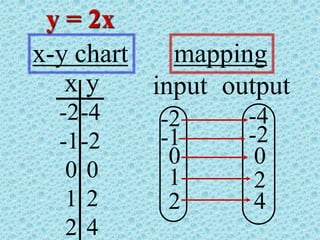
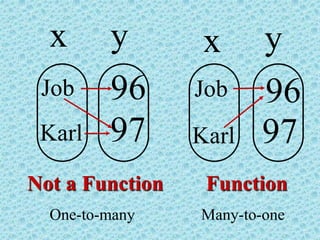
The document discusses the concepts of relations and functions, defining various types including linear, quadratic, constant, identity, and piecewise functions. It explains the criteria for determining if a relation is a function, such as the vertical line test, and introduces operation rules for functions, including addition, subtraction, multiplication, and division. Examples illustrate the evaluation of functions and their operations.

2. Relations
and
Functions

3. Relation - Any set of ordered
pairs.
domain- first coordinates,
input, independent variable
range- second coordinates,
output, dependent variable
Definitions

4. Example
• People and their heights
• Grades in General Mathematics

5. Example
Names
Peter
Krisha
Fay
Abby
Earl
Clara
Job
Karl
Audrey
Grades
95
94
93
92
95
97
94
90
98

6. Function -a type of relation
where there is exactly one
output for every input. For
every x there is exactly one y.

7. x y
Job
Karl
96
97
x y
Job
Karl
96
97
Not a Function Function

8. Vertical Line Test - Functions
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function

9. Vertical Line Test - Functions
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function Function

10. Vertical Line Test - Functions
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function Function Not a
Function

11. Vertical Line Test - Functions
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function Function Not a
Function
Function

12. Vertical Line Test - Functions
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function Function Not a
Function
Function
Not a
Function
Function Not a
Function
Not a
Function

13. Tell whether the relation below is a function.
1)
2)
3)
4)
input output
0
1
5
2
3
y
x
-3
-3
-3
-3
-1
0
1
2
x
y
Function
Not a
Function
Not a
Function
input output
-2
-1
0
3
4
5
6
Not a
Function

14. Conclusion and Definition
• Not every relation is a function.
• Every function is a relation.

15. TYPES OF FUNCTIONS
LINEAR FUNCTION
A function f is a linear function if
f(x) = mx + b, where m and b are real
numbers, and m and f(x) are not both
equal to zero.

16. y
x
-2
-1
0
1
2
-4
-2
0
2
4
y = 2x
input output
-2
-1
-4
-2
0
1
0
2
2 4
x-y chart mapping

17. QUADRATIC FUNCTION
A quadratic function is any
equation of the form f(x) =
ax2+ bx + c where a, b, and c
are real numbers and a ≠ 0.

18. y = x2 + 1
y
x
-2
-1
0
1
2
5
2
1
2
5
input output
-2
-1 5
2
0
1
1
2
x-y chart mapping

19. CONSTANT FUNCTION
A linear function f is a constant function if
f(x) = mx + b, where m = 0 and b is any
real number. Thus, f(x) = b.
IDENTITY FUNCTION
A linear function f is an identity function
if f(x) = mx + b, where m = 1 and b = 0.
Thus, f(x) = x.

20. Piecewise Function
A piecewise function or a compound
function is a function defined by
multiple sub-functions, where each sub-
function applies to a certain interval of
the main function's domain.

22. y
x
-2
-1
0
1
2
-4
-2
0
2
4
y = 2x
input output
-2
-1
-4
-2
0
1
0
2
2 4
x-y chart mapping

23. Many-to-one Function
if there are y values that have more
than one x value mapped onto them.
One-to-many (not a function)

24. x y
Job
Karl
96
97
x y
Job
Karl
96
97
Not a Function Function
One-to-many Many-to-one

25. Lesson 2 EVALUATION OF FUNCTIONS

26. EVALUATING FUNCTIONS
LAW OF SUBSTITUTION
If a + x = b and x = c, then a+ c= b
Example 1
If f(x) = x + 8, evaluate each.
a. f(4)
b. f(–2)
c. f(–x)
d. f(x + 3)

27. Function Notation
y 2x 3
  f (x) 2x 3
 
when x 1, y
 5
when x 2, y
 7
when x 3, y
  9
when x 4, y
 11
f (1)  5
f(2)  7
f (3)  9
f(4) 11
f( 4)
  5


28. 2
g(x) x
 h(x) 3x 2
 
Evaluate the following.
1) g(4) 
2) h( 2)
 
3) g( 3)
 
4) h(5) 
5) h(4) g(1)
 
6) h( 5) g( 2)
   
 
7) g h(3) 
 
8) h g(2) 
16
8

9

13
10  1 1

17
 4 6 8
 
g(7) 4 9

h(4) 10


29. Lesson 3 OPERATIONS ON FUNCTIONS

30. Lesson Objectives
At the end of the lesson, the students must
be able to:
• find the sum of functions;
• determine the difference between
functions;
• identify the product of functions;
• find the quotient between functions; and
• determine the composite of a function.

31. ADDITION OF FUNCTIONS
Let f and g be any two functions.
The sum f + g is a function whose
domains are the set of all real numbers
common to the domain of f and g, and
defined as follows:
(f + g)(x) = f(x) + g(x)

32. SUBTRACTION OF FUNCTIONS
Let f and g be any two functions.
The difference f – g is a function whose
domains are the set of all real numbers
common to the domain of f and g, and
defined as follows:
(f – g)(x) = f(x) – g(x)

33. MULTIPLICATION OF FUNCTIONS
Let f and g be any two functions.
The product fg is a function whose
domains are the set of all real numbers
common to the domain of f and g, and
defined as follows:
(fg)(x) = f(x) · g(x)

34. DIVISION OF FUNCTIONS
Let f and g be any two functions.
The quotient f/g is a function whose domains
are the set of all real numbers common to the
domain of f and g, and defined as follows: ,
where g(x) ≠ 0.
f
g
x
( ) =
f x
( )
g x
( )

35. Example 1
If f (x) = 3x – 2 and
g (x) = x2 + 2x – 3,
1. find (f + g) (x)
2. Find (f – g)(x)
3. Solve (fg)(x)
4. Find the quotient of f(x) and g(x)