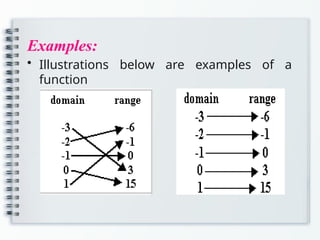
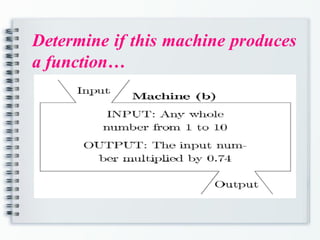
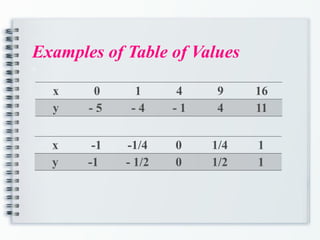
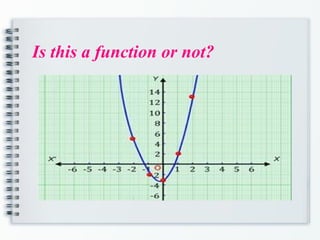
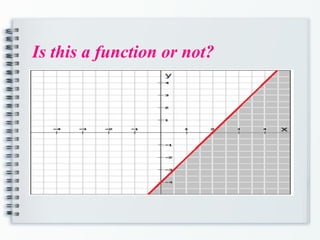
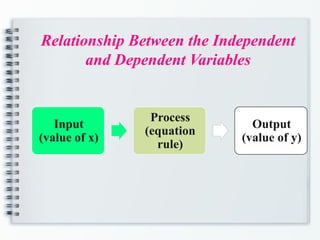
The document provides an overview of functions in mathematics, including definitions, relations versus functions, and methods for determining if a relation is a function. It explains concepts such as domain and range, evaluating functions, and operations on functions, including composite and piecewise functions. Additionally, it discusses even and odd functions with examples.

1. REVIEW ON FUNCTIONS
Module 1
GENERAL MATHEMATICS

2. What is a function?

3. Definition of a Function:
• It is a relation define as a set of ordered
pairs (x, y) where no two or more distinct
ordered pairs have the same first element
(x).
• Every value of x corresponds to a unique
value of y

4. Examples:
• Illustrations below are examples of a
function

5. Is it a function or not?

6. What is the difference
between a function and a
relation?

7. RELATIONS versus FUNCTIONS
RELATIONS FUNCTIONS
A relation is a rule that
relates values from a
set of values called the
domain to a second set
of values called the
range.
A function is a relation
where each element in
the domain is related to
only one value in the
range by some rule.

8. RELATIONS versus FUNCTIONS
RELATIONS FUNCTIONS
The elements of the
domain can be imagines
as input to a machine
that applies rule to
these inputs to generate
one or more outputs.
The elements of the
domain can be imagined
as input to a machine
that applies a rule so that
each input corresponds
to only one output.

9. RELATIONS versus FUNCTIONS
RELATIONS FUNCTIONS
A relation is also a set of
ordered pairs (x, y).
A function is a set of
ordered pairs (x, y) such
that no two ordered pairs
have the same x-value
but different y-values.

10. Is it a function or not?
a. f = {(0, -1), (2, -5), (4, -9), (6,-13)}
b. r ={(a, 0), (b, -1), (c, 0), (d, -1)}
c. g = (5, -10), (25, -50), (50, -100)
d. t = {(-2, 0), (-1, 1), (0, 1), (-2, 2)}

11. The function as a machine…
We will try to represent mathematical
relations as machines with an input
and an output, and that the output is
related to the input by some rule.

12. Determine if this machine produces
a function…

13. Determine if this machine produces
a function…

14. Determine if this machine produces
a function…

15. Determine if this machine produces
a function…

16. What is a table of
values?

17. Table of Values
a
• A table of values is commonly
observed when describing a function.
• This shows the correspondence
between a set of values of x and a set
of values of y in a tabular form.

18. Examples of Table of Values
a
x 0 1 4 9 16
y - 5 - 4 - 1 4 11
x -1 -1/4 0 1/4 1
y -1 - 1/2 0 1/2 1

19. Is it a function or not?
1.A jeepney and its plate number
2.A student and his ID number
3.A teacher and his cellular phone
4.A pen and the color of its ink

20. What is a vertical line
test?

21. Vertical Line Test
a
• The vertical line test for a function
states that if each vertical line
intersects a graph in the x-y plane at
exactly one point, then the graph
illustrates a function.

22. Is this a function or not?

23. Is this a function or not?

24. Is this a function or not?

25. Relationship Between the Independent
and Dependent Variables
Input
(value of x)
Process
(equation
rule)
Output
(value of y)

26. Examples:
1. Find the value of y in the equation
y = 10x – 3 if x = - 5.
2. Find the value of x if the value of y
in the equation is 2.

27. Applications:
1. A car has travelled a distance of 124
kilometers in 4 hours. Find the speed of the
car.
2. The volume of the cube is defined by the
function where s is the length of the edge.
• What is the volume of the cube if the
length of the edge is 5 cm?
• What is the length of its edge if its
volume is 728 cubic meters?

28. REVIEW ON FUNCTIONS
Module 1
EVALUATING FUNCTIONS

29. Evaluating Functions
a
• It is the process of determining the
value of the function at the number
assigned to a given variable.

30. Example:
Let . Find the following values of the
function
a. f (2)
b. f (-1)
c. f (0)
d. f (- ½ )
e. f (- 4)

31. Example:
Let . Find the following values of the
function
a. g (2)
b. g (4)
c. g (0)
d. g (9)
e. g (- 1/3)

32. Example:
Let h. Find the following values of the
function
a. h (1)
b. h (-2)
c. h (6)
d. h (0)
e. h (2)

33. REVIEW ON FUNCTIONS
Module 1
DOMAIN AND RANGE OF
FUNCTIONS

34. Domain D of a Function
a
• It is the set of all x-coordinates in the
set of ordered pairs.
Range R of a Function
a
• It is the set of all y-coordinates in the
set of ordered pairs.

35. Determine the domain and the range
of the following:
a x 0 1 4 9 16
y - 5 - 4 - 1 4 11
x -1 -1/4 0 1/4 1
y -1 - 1/2 0 1/2 1

36. More on Independent Variables
a
• There are instances in which not all
values of the independent variables
are permissible.
• That is, some functions have
restrictions.

37. Determine the domain and the range
of the following:
a

38. Piece-wise Functions
a
• These are functions which are defined
in defined in different domains since
they are determined by several
equations.

39. Determine the domain and the range
of the following:
a { 2x + 3 if x ≠ 2
4 if x = 2
{ 2x + 3 if x < 1
– if x 1

40. REVIEW ON FUNCTIONS
Module 1
OPERATIONS ON
FUNCTIONS

41. Operations on Functions
If f and g are functions then
• (f + g) = f(x) + g(x)
• (f – g) = f(x)– g(x)
• (f g) = f(x) g(x)
• where g(x) ≠ 0

42. Example
Let f(x) = and g(x)= x – 1. Perform the
operations and identify the domain
• (f + g)
• (f – g)
• (f g)

43. Example
Let f(x)= x – 3 and g(x) = . Perform the
operations and identify the domain
• (f + g)
• (f – g)
• (f g)

44. REVIEW ON FUNCTIONS
Module 1
COMPOSITE FUNCTIONS

45. Operations on Functions
If f and g are functions then the
composite function denoted by , is
defined by

46. Operations on Functions
The domain of is the set of all numbers
x in the domain of g such that g(x) is in
the domain of f.

47. Example
Let f(x)= x – 3 and g(x) = . Find
• )(x)
• )(x)
• )(3)
• )(- 4)

48. REVIEW ON FUNCTIONS
Module 1
EVEN AND ODD
FUNCTIONS

49. Even and Odd Functions
• A function f is said to be even if
f(–x)=f(x) for each value of x in the
domain of f.
• A function f is said to be odd if
f(–x)= – f(x) for each value of x in the
domain of f.

50. Example
Determine whether each of the following
functions is even, odd or neither