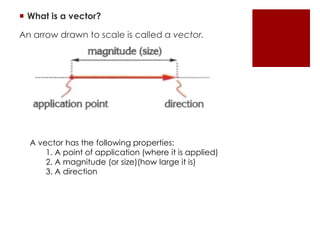
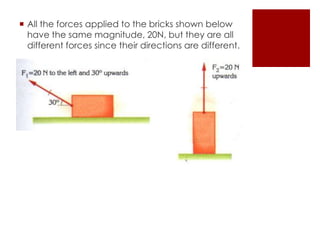
A vector has magnitude and direction and can be represented by an arrow. There are two types of quantities: scalar quantities which only have magnitude (like mass), and vector quantities which have both magnitude and direction (like force). Forces are added using the head-to-tail method, and the net or resultant force is a single force equal to the combined effect. Forces can also produce turning effects called moments. For an object to be in equilibrium, the sums of opposing forces and opposing moments must be equal.

1. Representing Force

2. What is a vector?
 QUANTITIES IN SCIENCE
 There are two types of quantities in science:
Scalar quantities.
Vector quantities

3.  Scalar quantity: It is a quantity which has only
magnitude. They can be totally described by a
number and a unit.
Volume, area, temperature, energy, speed, mass
, time are all scalar quantities.
 Vector quantity: It is a quantity which has both
magnitude and direction.
Force, velocity, acceleration, and displacement
are vector quantities.

4.  What is a vector?
An arrow drawn to scale is called a vector.
A vector has the following properties:
1. A point of application (where it is applied)
2. A magnitude (or size)(how large it is)
3. A direction

5.  All the forces applied to the bricks shown below
have the same magnitude, 20N, but they are all
different forces since their directions are different.

6. Example:
 Show the following forces using vectors.
a) A block is pulled to the east with a force of 4 N.
b) A chest is pulled to the southwest with a force of
3 N.
c) Three forces act on a block to move it, one with
2 N due north, one with 3 N due east and one
with 3 N due west.

7. COMBINING FORCES
 Resultant force (R): It isa single force which has
the same effect as two or more forces acting
together.
 Component forces: They are the forces that form
a resultant.
The arrowhead ( ) over each letter shows that it is a vector
quantity, which means the quantity also has a direction.

8. Rule for addition of vectors
(forces):
 Rule for addition of vectors (forces):
1. Add the forces head to tail without changing their magnitude
and direction
2. Draw a force from the tail of the first to the head of the last.

9.  Combining Forces Acting in the Same Direction
 To find the magnitude of a resultant of two forces
acting in the same direction we add the
magnitudes of the components.

10.  Combining Forces Acting in Opposite Directions
 Let F1 and F2 be forces in opposite directions and
let F1 be greater than F2. Then the magnitude of
the resultant is The direction of the resultant force
is in the direction of the greater force.

11. Example:
 What will be the net force on the box in the figure
below, if it is pulled by the two different forces in
opposite directions?

12. TURNING EFFECT OF FORCES
 If a force is applied on a body which is
suspended, hinged or pivoted, the force may
cause the body to turn.

13. Moment of force
 The turning effect of the force is called moment.

14. Conditions for Equilibrium
 There are two conditions for equilibrium:
1. The sum of the forces in one direction must be
equal to the sum of the forces in the opposite
direction.

15. Conditions for Equilibrium
2. The sum of the clockwise moments about any
point must be equal to the sum of the anti-
clockwise moments.