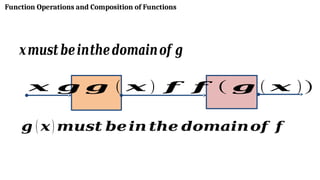
The document discusses function operations and composition of functions, explaining how to add, subtract, multiply, or divide two functions to create a new function while considering their domains. It provides multiple sample problems with detailed solutions, illustrating the operations and the determination of domains for various function combinations. Additionally, it covers the concept of decomposing composite functions into simpler components.