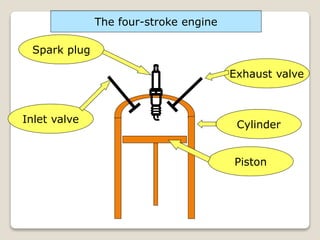
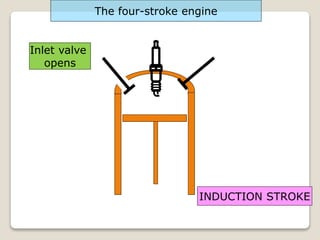
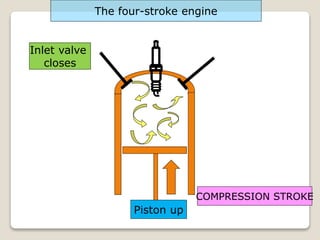
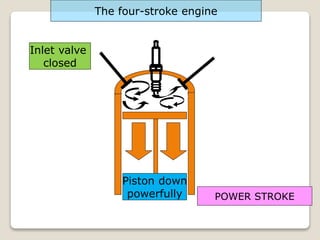
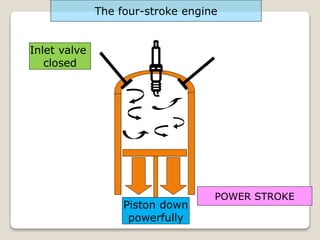
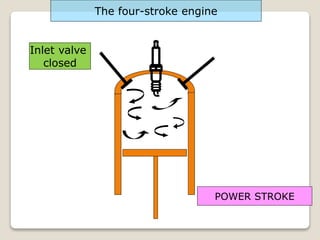
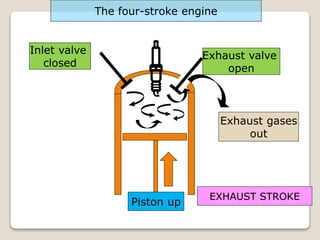
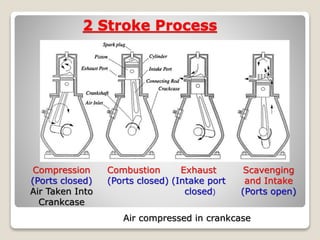
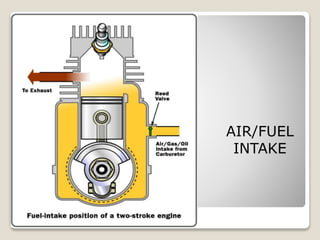
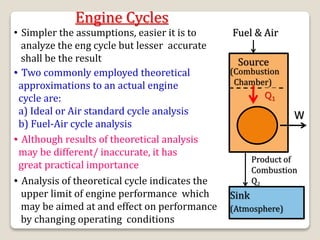
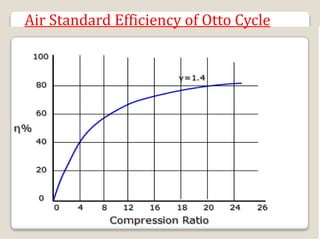
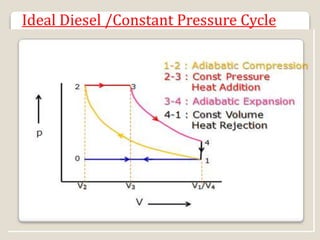
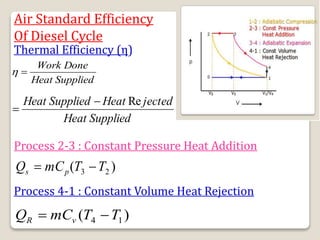
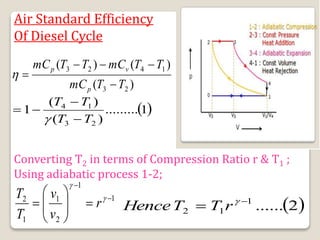
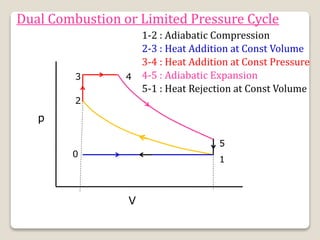
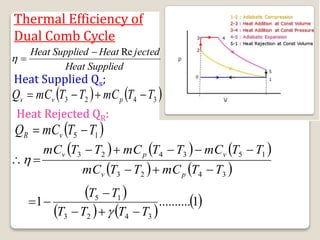
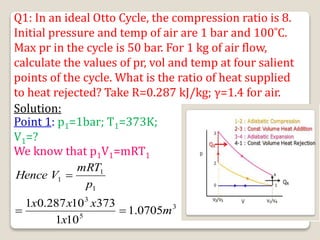
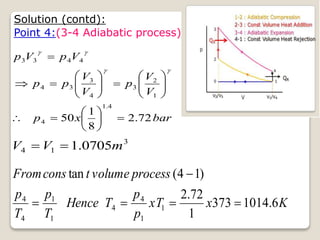
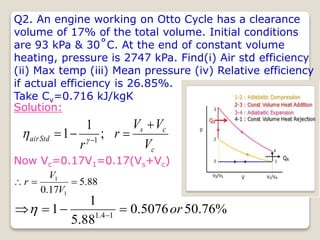
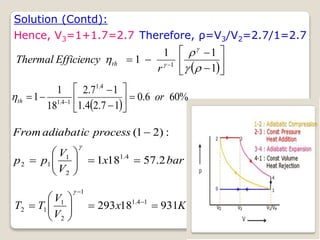
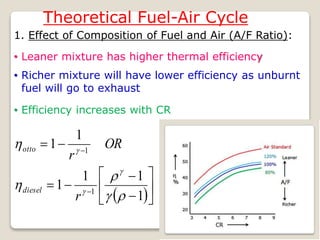
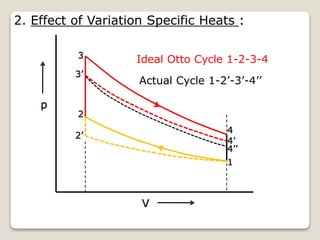
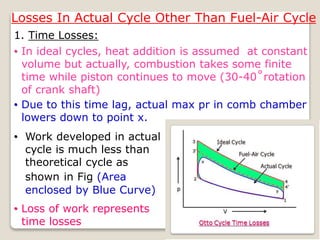
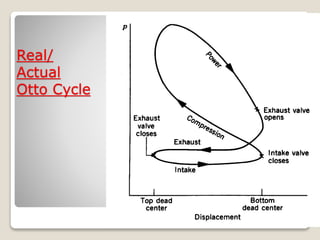
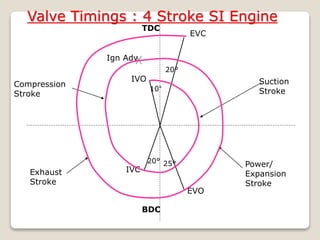
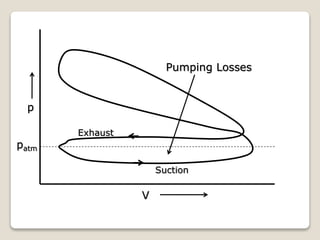
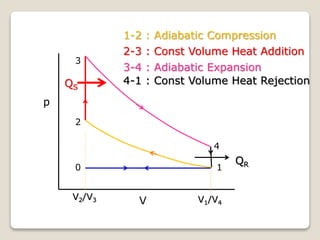
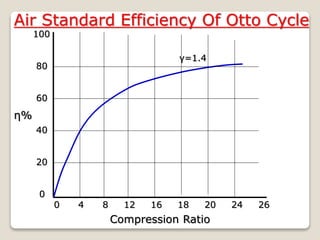
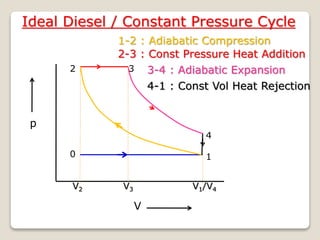
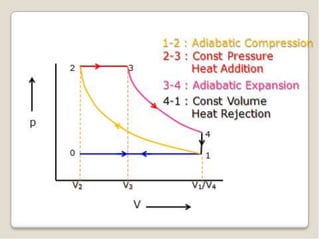
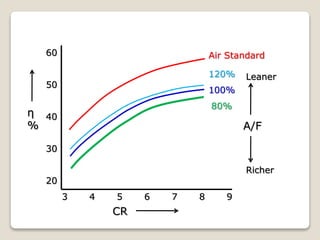
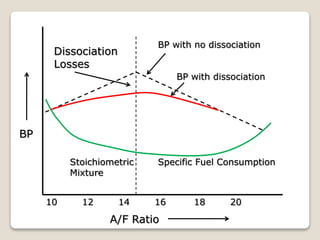
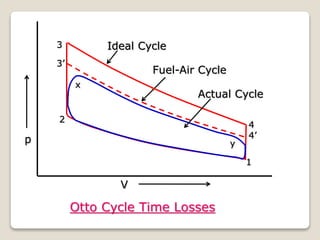
The document outlines the four-stroke engine cycle, detailing the four distinct stages: intake, compression, combustion, and exhaust, with explanations of valve operations during each phase. It also discusses theoretical analyses of internal combustion engine cycles, emphasizing the importance of simplifying assumptions such as treating the working medium as an ideal gas. Additionally, the document compares different engine cycles, including Otto and Diesel cycles, providing insights into their efficiencies and operational principles.